离散数学_第二章:基本结构:集合、函数、序列、求和和矩阵(1)
集合与函数
- 2.1 集合
- 2.1.1 集合的基本概念
- 2.1.2 集合的表示方法
- 2.1.3 文氏图
- 2.1.4 证明集合相等
- 2.1.5 集合的大小 ——基
- 2.1.6 幂集
- 2.1.7 集族、指标集
- 2.1.8 笛卡尔积
- 2.1.9 容斥原理
2.1 集合
2.1.1 集合的基本概念
定义1:集合 是不同对象的一个无序的聚集,对象也称为集合的元素(element)或成员(member)。集合包含(contain)它的元素。我们用a∈A来表示a是集合A 中的一个元素。记号a∉A表示a不是集合A 中的一个元素。
定义2:集合相等 两个集合相等当且仅当它们拥有同样的元素
。如果A和B是集合,则A和B是相等的当且仅当∀x (x∈A ↔ x∈B)。如果A和B是相等的集合,就记为 A=B。
定义3:空集 有一个特殊的不含任何元素的集合。这个集合称为空集。
定义4:单元素集 只有一个元素的集合叫作单元素集。
定义5:子集 集合A是集合B的子集并且B是A的超集当且仅当A的每个元素也是B的元素。
我们用记号A ⊆ B表示集合A是集合B的子集。另外,如果我们要强调B是A的超集,可以用等价的记号 B ⊇ A(故 A ⊆ B和B⊇A是等价的语句)。
定义6:n元集 :含有n个元素的集合
0元集:∅
1元集(或单元集),如{a}, {b}, {∅}, {{∅}}······
定义7:相对补集 :属于A而不属于B的全体元素,称为B对A的相对补集,记作A-B。A-B = { x | (x∈A) ∧ (x∉B) }
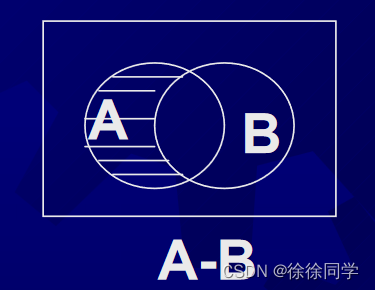
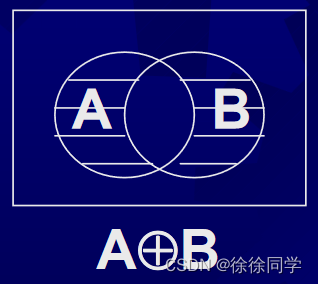
定义8:对称差 :属于A而不属于B,或属于B而不属于A的全体元素,称为A与B的对称差,记作A⊕B。A⊕B={x|(x∈A∧x∉B)∨(x∉A∧x∈B)}
A⊕B=(A-B)∪(B-A)=(A∪B)-(A∩B)
2.1.2 集合的表示方法
1.花名册方法
(也叫:枚举法、列举法)
🐤列出集合中的全体元素,元素之间用逗号分开,然后用花括号括起来。例如:
A = {a,b,c,d,…,x,y,z}
B = {0,1,2,3,4,5,6,7,8,9}
🐤集合元素的顺序不重要:
C={2,1}={1,2}
🐤集合中的元素各不相同(多重集除外):
C={2,1,1,2}={2,1}
🏔多重集(multiple set):
允许元素多次重复出现的集合
元素的重复度: 元素的出现次数(≥0)
例如:A = {a,a,b,b,c}是多重集
元素a,b的重复度是2
元素c的重复度是1
元素d的重复度是0
🐤当集合中元素特征明确 或者规律显而易见时,可以使用省略号 (···)代替,不必列出所有成员:
S = { a,b,c, ······ ,z }
2.使用集合构造器符号
(也叫:描述法)
通过描述作为集合的成员必须具有的 性质来刻画集合中的那些元素。一般的形式是采用记号 {x | x具有性质P} ,读作:满足 P的所有x的集合
常用的数集合:
N = {0,1,2,3, ···}:自然数(natural numbers)集合
Z = {··· ,-2,-1,0,1,2 ···}:整数(integers)集合
Q = {p/q | p∈Z,q∈Z,且q ≠ 0 }:有理数(rational numbers)集合
R:实数(real numbers)集合
C:复数(complex numbers)集合
这些集合通常用黑体表示
3.特征函数法
集合A的特征函数是χA (x)
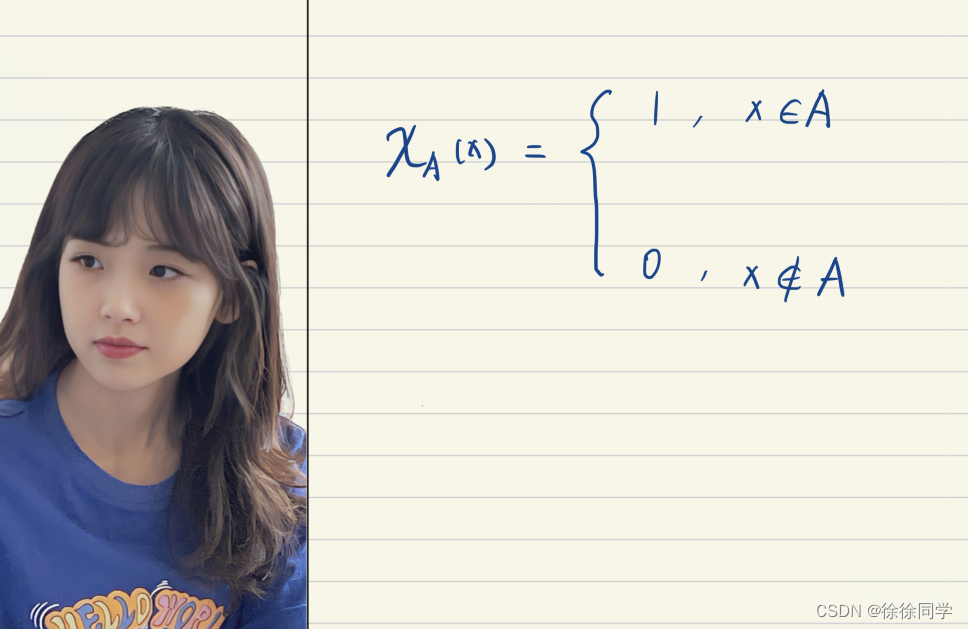
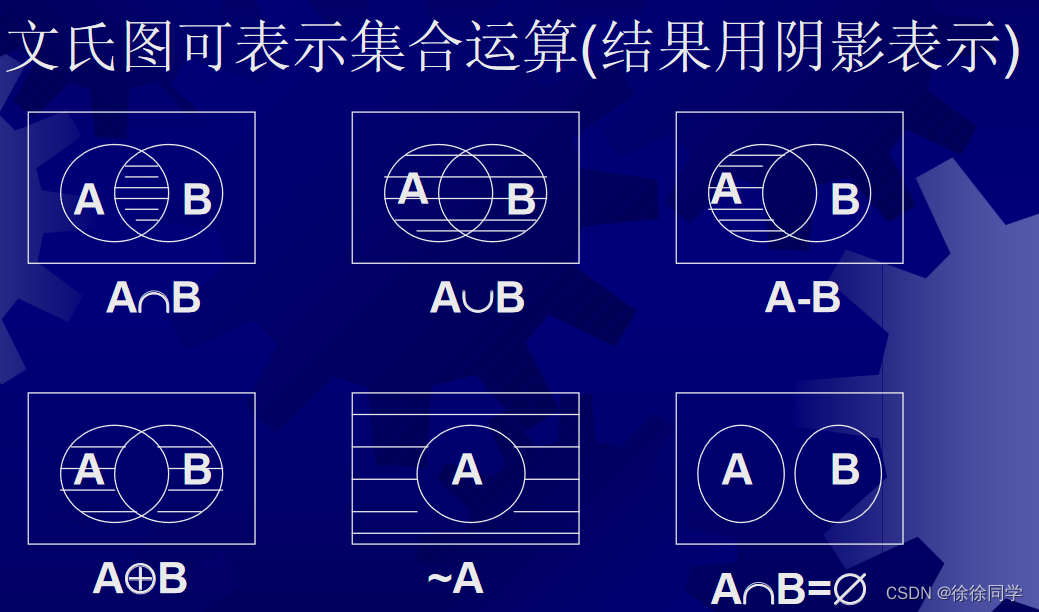
2.1.3 文氏图
文氏图: 平面上的n个圆(或椭圆),使得任何可能的相交部分, 都是非空的和连通的

2.1.4 证明集合相等
需要证明:A ⊆ B 和 B ⊆ A
2.1.5 集合的大小 ——基
令S为集合,如果S中恰有n个不同的元素,这里n是非负整数,我们就说S是有限集(一个集合称为是无限的,如果它不是有限的),而n是S的基数,S的基数记为 | S |
➡ 通俗来说,基数就是元素的个数
2.1.6 幂集
幂集: 给定集合S,S的幂集是集合S 所有子集的集合 。S的幂集记作P(S)
例如: A={a,b}, P(A) = {∅,{a},{b},{a,b}}
🐳 x∈P(A) ⇔ x⊆A
定理: |A|=n ⇒ |P(A)|=2n

2.1.7 集族、指标集
集族定义: 由集合构成的集合(幂集都是集族)
指标集定义: 设A是集族, 若A={Aα|α∈S}, 则S称为A的指标集. S中的元素与A中的集合是一一对应的. 也记作A={Aα|α∈S}={Aα}α∈S
2.1.8 笛卡尔积
🚩有序n元组:(a1,a2,···,an)是以a1为第1个元素,a2为第2
个元素,⋯,an为第n个元素的有序聚集。
⭐两个有序n元组是相等的当且仅当每一对对应的元素都相等
特别地,有序二元组称为序偶。
🚩笛卡尔积:
令A和B为集合。A和B的笛卡儿积用 A×B表示,是所有序偶(a,b)的集合,其中a∈A,b∈B。于是,A×B = {(a,b)| a∈A∧b∈B}
注意:笛卡尔积A×B和B×A是不相等的,除非A = ∅,B = ∅或A = B
2.1.9 容斥原理
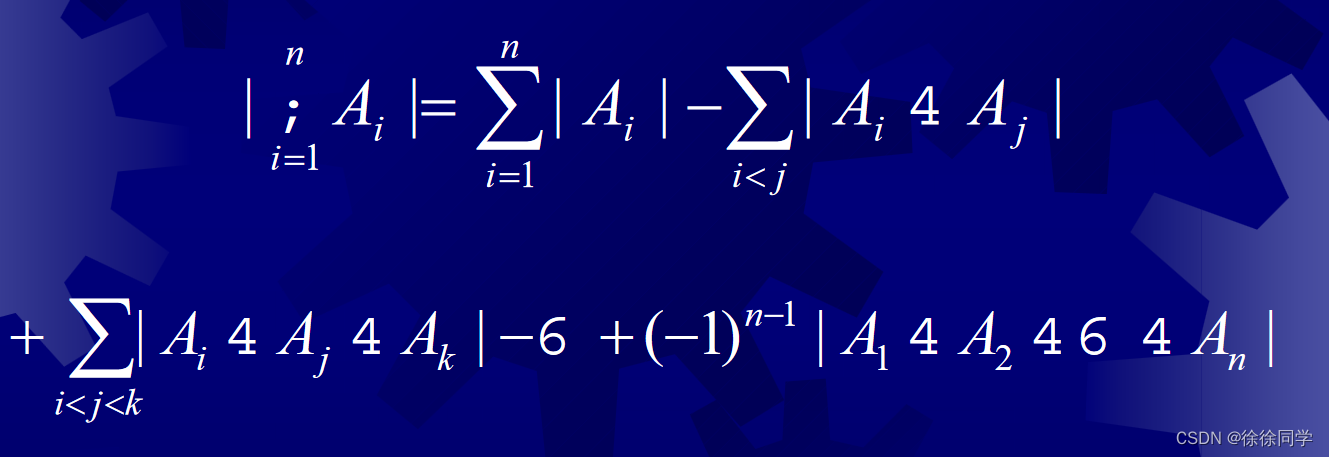 |A ∪ B| = |A|+|B| - |A∩B|
|A ∪ B| = |A|+|B| - |A∩B|
相关文章:
离散数学_第二章:基本结构:集合、函数、序列、求和和矩阵(1)
集合与函数2.1 集合 2.1.1 集合的基本概念 2.1.2 集合的表示方法 2.1.3 文氏图 2.1.4 证明集合相等 2.1.5 集合的大小 ——基 2.1.6 幂集 2.1.7 集族、指标集 2.1.8 笛卡尔积 2.1.9 容斥原理2.1 集合 2.1.1 集合的基本概念 定义1:集合 是不同对象的一个无序的聚…...

ChatGPT想干掉开发人员,做梦去吧
很多人都发现ChatGPT可以做一些代码相关的工作,不仅可以写一些基础的类似python、java、js的代码段,还可以做一定量的调优,于是就开始担忧起来,到哪天我的开发工作会不会被ChatGPT这个工具给取代了? 目录 1. ChatGPT…...
尚硅谷大数据技术Hadoop教程-笔记04【Hadoop-MapReduce】
视频地址:尚硅谷大数据Hadoop教程(Hadoop 3.x安装搭建到集群调优) 尚硅谷大数据技术Hadoop教程-笔记01【大数据概论】尚硅谷大数据技术Hadoop教程-笔记02【Hadoop-入门】尚硅谷大数据技术Hadoop教程-笔记03【Hadoop-HDFS】尚硅谷大数据技术Ha…...
Linux信号sigaction / signal
Linux信号sigaction / signal 文章目录Linux信号sigaction / signal目的函数原型struct sigaction信号枚举值ISO C99 signals.Historical signals specified by POSIX.New(er) POSIX signals (1003.1-2008, 1003.1-2013).Nonstandard signals found in all modern POSIX system…...

坦克大战第一阶段代码
package tanke.game;import javax.swing.*; import java.awt.*; import java.awt.event.KeyEvent; import java.awt.event.KeyListener; import java.util.Vector;//为了监听键盘事件,实现keylistener public class mypanel extends JPanel implements KeyListener …...
博客系统前端实现
目录 1.预期效果 2.实现博客列表页 3.实现博客正文页 4.实现博客登录页 5.实现博客编辑页面 1.预期效果 对前端html,css,js有大致的了解后,现在我们实现了一个博客系统的前端页面.一共分为四个页面没分别是:登陆页面,博客列表页,博客正文页,博客编辑页 我们看下四个界面…...
ChatGPT技术原理、研究框架,应用实践及发展趋势(附166份报告)
一、AI框架重要性日益突显,框架技术发展进入繁荣期,国内AI框架技术加速发展: 1、AI框架作为衔接数据和模型的重要桥梁,发展进入繁荣期,国内外框架功能及性能加速迭代; 2、Pytorch、Tensorflow占据AI框…...

【屏幕自适应页面适配问题】CSS的@media,为了适应1440×900的屏幕,使用@media解决问题
文章目录bug修改实例CSS3 media 查询CSS 多媒体查询,适配各种设备尺寸bug修改实例 <template><div id"deptAllDown" style"height: 400px;width:880px"/> </template>为了适应1440900的屏幕,使用media解决问题 …...
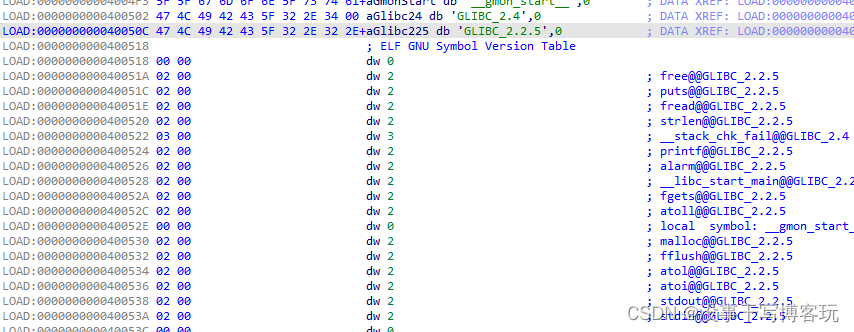
一篇文章理解堆栈溢出
一篇文章理解堆栈溢出引言栈溢出ret2text答案ret2shellcode答案ret2syscall答案栈迁移答案堆溢出 unlink - UAF堆结构小提示向前合并/向后合并堆溢出题答案引言 让新手快速理解堆栈溢出,尽可能写的简单一些。 栈溢出 代码执行到进入函数之前都会记录返回地址到SP…...

优化模型验证关键代码27:多旅行商问题的变体-多起点单目的地问题和多汉密尔顿路径问题
目录 1 多起点单目的地问题(Multiple departures single destination mTSP) 1.1 符号列表 1.2 数学模型 1.4 解的可视化结果...
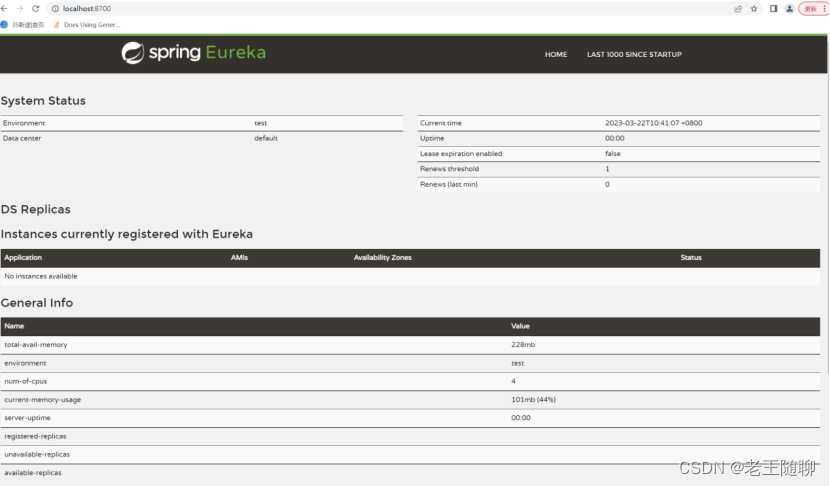
快速搭建第一个SpringCloud程序
目录 1、Spring Boot项目脚手架快速搭建 1.1 生成工程基本配置 1.2 生成工程。 1.3 导入开发工具(此处为Idea) 1.4 运行代码 1.5 验证是否能访问 2、Spring Cloud环境搭建 2.1 版本匹配问题 2.2 Spring Cloud环境测试 3、引入Eureka Server 3…...
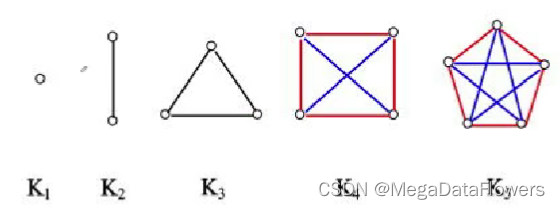
【离散数学】图论
1、有n个点没有边 零图 2、有1个点没有边 平凡图 3、含有平行边的图 多重图 4、简单图 不含有平行边和自回环的图 5、任意两个结点之间都有边 完全图 6、环贡献 两度 7、所有顶点的度数之和等于边数的两倍 8、在有向图中所有顶点的出度之和 或者 入度之和 等于边数 9、度数为…...

代码随想录算法训练营第三十七天-贪心算法6| 738.单调递增的数字 968.监控二叉树 总结
738.单调递增的数字 贪心算法 题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。 例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--&#…...
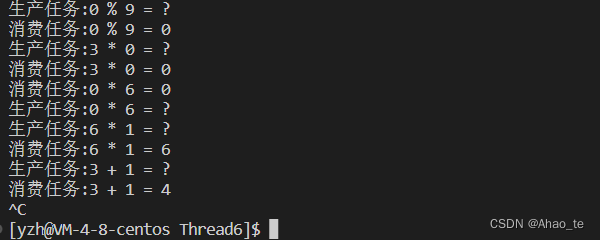
【Linux】线程中的互斥锁、条件变量、信号量(数据安全问题、生产消费模型、阻塞队列和环形队列的实现)
文章目录1、线程互斥1.1 线程间频繁切换导致的问题1.2 使用互斥锁1.3 互斥锁的原理1.4 线程中的数据安全问题2、线程同步之条件变量2.1 生产消费模型2.2 条件变量概念和调用函数2.3 阻塞队列的实现3、线程同步之信号量3.1 理解信号量3.2 信号量接口3.3 环形队列的实现4、小结1、…...

MySQL8.0的安装和配置
🎉🎉🎉点进来你就是我的人了 博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习! 欢迎志同道合的朋友一起加油喔🦾&am…...
LinuxGUI自动化测试框架搭建(三)-虚拟机安装(Hyper-V或者VMWare)
(三)-虚拟机安装(Hyper-V或者VMWare)1 Hyper-V安装1.1 方法一:直接启用1.2 方法二:下载安装1.3 打开Hyper-V2 VMWare安装注意:Hyper-V或者VMWare只安装一个,只安装一个,只…...
,包含copypaste、翻转、cutout等八种增强方式)
改进YOLO系列:数据增强扩充(有增强图像和标注),包含copypaste、翻转、cutout等八种增强方式
这里写目录标题 一、简介二、数据增强方法介绍复制-粘贴(Copy-paste)翻转(Flip)Cutout加噪声(Noise)亮度调整(Brightness)平移(Shift)旋转(Rotation)裁剪(Crop)copy-paste的代码一、简介 数据增强是一种通过对原始数据进行随机变换、扰动等操作来生成新的训练样…...
(std::stack)(一))
c++11 标准模板(STL)(std::stack)(一)
定义于头文件 <stack> template< class T, class Container std::deque<T> > class stack;std::stack 类是容器适配器,它给予程序员栈的功能——特别是 FILO (先进后出)数据结构。 该类模板表现为底层容器的包装…...
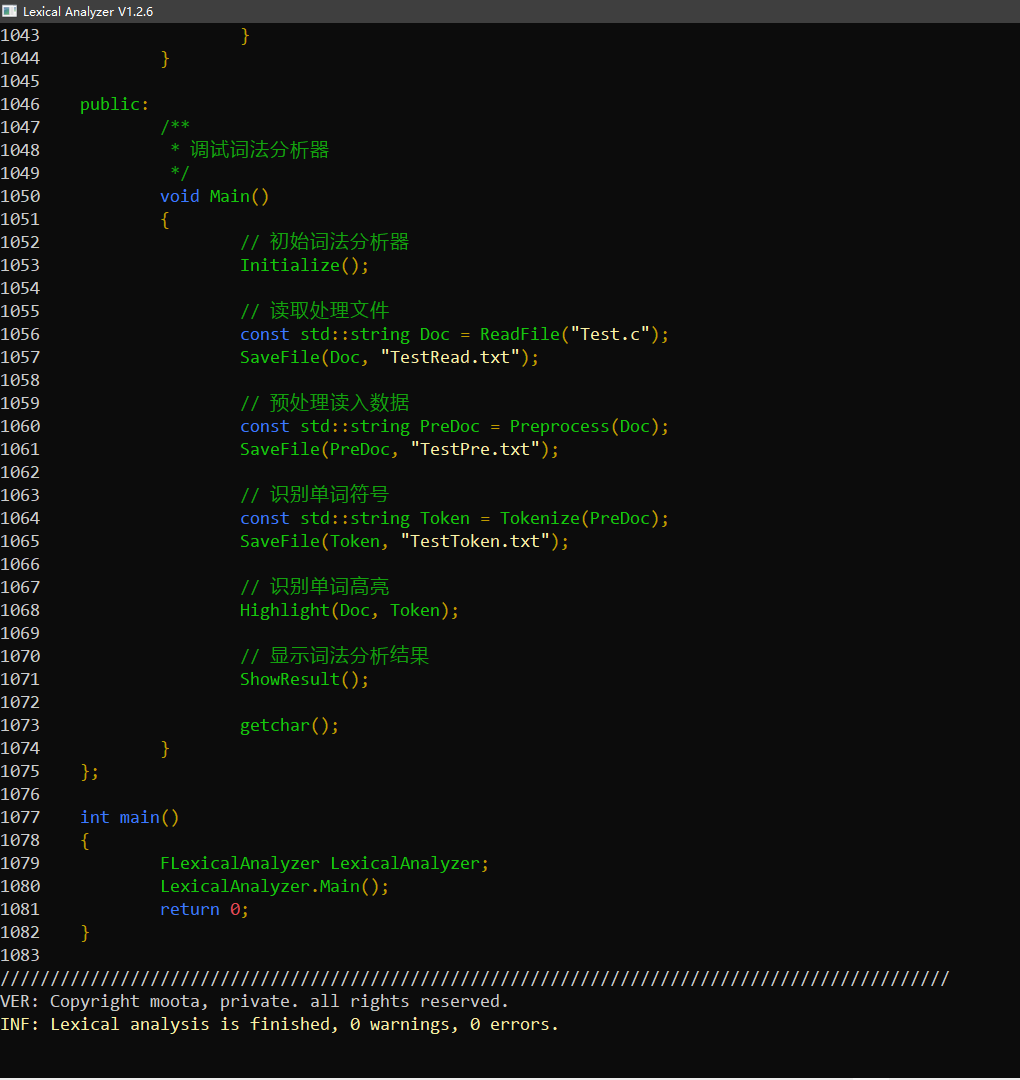
C++-c语言词法分析器
一、运行截图 对于 Test.c 的词法分析结果 对于词法分析器本身的源代码的分析结果 二、主要功能 经过不断的修正和测试代码,分析测试结果,该词法分析器主要实现了以下功能: 1. 识别关键字 实验要求:if else while do for main…...

Maven工具复习
Maven从入门到放弃Maven概述Maven 的配置Maven的基本使用IDEA 配置MAVENMaven坐标IDEA 创建MavenIDEA 导入Maven关于右侧Maven小标签(也就是Maven面板)找不到问题的解决办法关于不小心把IDEA主菜单搞消失的解决办法依赖管理Maven概述 Maven是一个工具提供了一套标准的项目结构…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
