算法训练day2:哈希表
哈希表理论基础
哈希表是根据关键码的值而直接进行访问的数据结构。
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法!
常见的三种哈希结构
当我们想使用哈希法来解决问题的时候,我们一般会选择如下三种数据结构。
- 数组
- set (集合)
- map(映射)
这里数组就没啥可说的了,我们来看一下set。
在C++中,set 和 map 分别提供以下三种数据结构,其底层实现以及优劣如下表所示:

std::unordered_set底层实现为哈希表,std::set 和std::multiset 的底层实现是红黑树,红黑树是一种平衡二叉搜索树,所以key值是有序的,但key不可以修改,改动key值会导致整棵树的错乱,所以只能删除和增加。
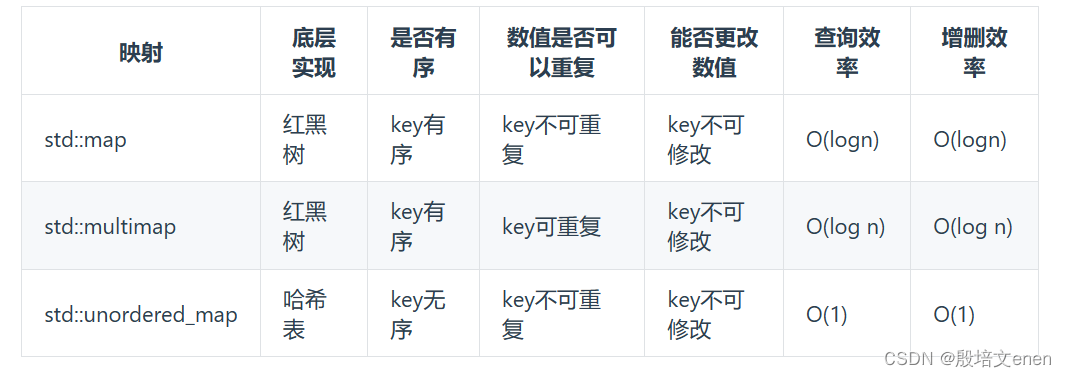
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就用multiset。
那么再来看一下map ,在map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的,因为key的存储方式使用红黑树实现的。
其他语言例如:java里的HashMap ,TreeMap 都是一样的原理。可以灵活贯通。
虽然std::set、std::multiset 的底层实现是红黑树,不是哈希表,std::set、std::multiset 使用红黑树来索引和存储,不过给我们的使用方式,还是哈希法的使用方式,即key和value。所以使用这些数据结构来解决映射问题的方法,我们依然称之为哈希法。 map也是一样的道理。
这里在说一下,一些C++的经典书籍上 例如STL源码剖析,说到了hash_set hash_map,这个与unordered_set,unordered_map又有什么关系呢?
实际上功能都是一样一样的, 但是unordered_set在C++11的时候被引入标准库了,而hash_set并没有,所以建议还是使用unordered_set比较好,这就好比一个是官方认证的,hash_set,hash_map 是C++11标准之前民间高手自发造的轮子。
242:有效字母的异位词
class Solution {
public:bool isAnagram(string s, string t) {int record[26] = {0};for (int i = 0; i < s.size(); i++) {record[s[i] - 97]++;}for (int i = 0; i < t.size(); i++) {record[t[i] - 97]--;}for (int i = 0; i < 26; i++) {if (record[i] != 0) {return false;}}return true;}
};349:两个数组的交集
使用数组做哈希表
class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> result_set; // 存放结果,之所以用set是为了给结果集去重int hash[1005] = {0}; // 默认数值为0for (int num : nums1) { // nums1中出现的字母在hash数组中做记录hash[num] = 1;}for (int num : nums2) { // nums2中出现话,result记录if (hash[num] == 1) {result_set.insert(num);}}return vector<int>(result_set.begin(), result_set.end());}
};使用unordered_set
class Solution {
public:vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {unordered_set<int> result_set; // 存放结果,之所以用set是为了给结果集去重unordered_set<int> nums_set(nums1.begin(), nums1.end());for (int num : nums2) {// 发现nums2的元素 在nums_set里又出现过if (nums_set.find(num) != nums_set.end()) {result_set.insert(num);}}return vector<int>(result_set.begin(), result_set.end());}
};202:快乐数
class Solution {
public:int getSum(int n){int sum = 0;while(n){sum += (n % 10) * (n % 10);n /= 10;}return sum;}bool isHappy(int n) {unordered_set<int>set;while(1){int sum = getSum(n);if(sum == 1){return true;}if(set.find(sum) != set.end()){return false;}else{set.insert(sum);}n = sum;}}
};1:两数之和
map方法
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int,int>map;for(int i = 0;i<nums.size();i++){auto tmp = map.find(target - nums[i]);if(tmp != map.end()){return {tmp->second,i};}else{map.insert(pair<int, int>(nums[i], i));}}return {};}
};454:四数相加
class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {unordered_map<int, int> umap; //key:a+b的数值,value:a+b数值出现的次数for (int a :nums1) {for (int b : nums2) {umap[a + b]++;}}int count = 0; for (int c : nums3) {for (int d : nums4) {if (umap.find(0 - (c + d)) != umap.end()) {count += umap[0 - (c + d)];}}}return count;}
};15:三数之和(没搞明白,有哈希和双指针两种办法,下面是双指针法)
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(), nums.end());// 找出a + b + c = 0// a = nums[i], b = nums[left], c = nums[right]for (int i = 0; i < nums.size(); i++) {// 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了if (nums[i] > 0) {return result;}// 错误去重a方法,将会漏掉-1,-1,2 这种情况/*if (nums[i] == nums[i + 1]) {continue;}*/// 正确去重a方法if (i > 0 && nums[i] == nums[i - 1]) {continue;}int left = i + 1;int right = nums.size() - 1;while (right > left) {// 去重复逻辑如果放在这里,0,0,0 的情况,可能直接导致 right<=left 了,从而漏掉了 0,0,0 这种三元组/*while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;*/if (nums[i] + nums[left] + nums[right] > 0) right--;else if (nums[i] + nums[left] + nums[right] < 0) left++;else {result.push_back(vector<int>{nums[i], nums[left], nums[right]});// 去重逻辑应该放在找到一个三元组之后,对b 和 c去重while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;// 找到答案时,双指针同时收缩right--;left++;}}}return result;}
};使用数组和set来做哈希法的局限。
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
map是一种<key, value>的结构,本题可以用key保存数值,用value在保存数值所在的下标。所以使用map最为合适。
C++提供如下三种map::(详情请看关于哈希表,你该了解这些! (opens new window))
- std::map
- std::multimap
- std::unordered_map
std::unordered_map 底层实现为哈希,std::map 和std::multimap 的底层实现是红黑树。
同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解),1.两数之和 (opens new window)中并不需要key有序,选择std::unordered_map 效率更高!
相关文章:

算法训练day2:哈希表
哈希表理论基础 哈希表是根据关键码的值而直接进行访问的数据结构。 当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。 但是哈希法也是牺牲了空间换取了时间,因为我们要使用额外的数组,set或者是map来存放数据&#…...

Git——利用SSH密钥本地仓库上传远程GitHub库
文章目录 1、前言2、详细步骤2.1 创建密钥2.2 进入密钥文件并复制2.3 在GitHub上添加密钥2.4 回到本地仓库文件夹,连接GitHub并上传 3. 结语 1、前言 现在想要从本地设备将本地仓库上传到GitHub上需要用到SSH密钥,接下来讲解大致的步骤,本文默…...
一起读源码 —— Fastjson 的核心方法及其实现原理
源码介绍 Fastjson 是阿里巴巴开源的一个 Java 工具库,它常常被用来完成 Java 的对象与 JSON 格式的字符串的相互转化。 此文读的源码是撰写此文时 Fastjson 的最新的发布版本,即 1.2.83 下载源码 请前去 github 找到 release 最新版下载后解压&…...
Python实现批量图片下载及去重处理
背景 在爬虫应用开发中,常常需要批量下载图片,并对图片进行去重处理。Python 是一种非常流行的编程语言,也是开发爬虫应用的首选,本文将介绍如何使用 Python 下载图片,并对下载的图片进行去重处理。 内容 首先&…...

【QA】Python代码调试之解决Segmentation fault (core dumped)问题
Python代码调试之解决Segmentation fault 问题 问题描述排查过程1. 定位错误,2. 解决办法 参考资料 问题描述 Python3执行某一个程序时,报Segmentation fault (core dumped)错,且没有其他任何提示,无法查问题。 Segmentation fa…...
)
C++ 迭代器之旅(Journey of Iterators)
C 迭代器之旅(Journey of Iterators) 一、引言(Introduction)C Iterator模板库简介(Overview of C Iterator Template Library)Iterator的重要性和作用(The Importance and Role of Iterators&a…...

使用全球融合CDN的10大优势
根据预估,今年的全球内容交付网络(CDN)市场预计将达到424亿美元。而由于移动应用程序的激增和人工智能尤其是ChatGPT等相关领域的快速发展将进一步带来CDN市场的快速增长,可以说全球CDN的黄金时代才刚开始。 融合CDN和多CDN战略是…...
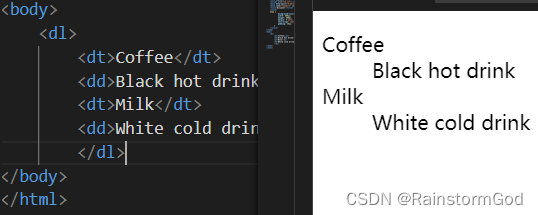
前端学习:HTML图像、表格、列表
目录 图像 一、图像标签和源属性(Src) 二、替换文本属性(Alt) 三、设置图片样式基本属性 四、图像标签 表格 一、标签 补充: 二、表格的表头 三、表格常用标签和属性 标签 属性 列表 一、无序列表 二、有序列表 三、定义列表 四、列表常用标签属性 图像 一、…...

202305读书笔记|《因思念而沉着》——任何赞美都是身外之物唯自由可随身携带
《因思念而沉着》作者巴哑哑,忘了是什么时候加入的书架,昨天下班地铁上读完的书。是美的! 部分节选如下: 羽叶茑萝举着熄灭的花青色的小枣落了一地所以哭泣沾染上了你的脸 在没落下 当我们开始生活 就是开始患上了眼疾你独自悲伤…...
M1 M2上能安装上Autocad 2024 Mac 中文版吗 autocad m1 m2版本有啦 终于支持Ventura 13x了
AutoCAD是一款强大的工具,适合于各种领域的设计和绘图。它具有二维图形和三维建模功能、多种文件格式支持、自定义命令和样式、批处理和脚本等特点,可以帮助用户实现高质量的设计和建模。同时,还支持云端存储和共享,方便用户随时随…...

【题解】P4055 [JSOI2009] 游戏
link 题目大意 题目说得比较清楚。 题解 前置知识:二分图最大匹配、基础博弈论。 每个点只能走一次的四联通点阵,可以想到二分图匹配。 将其套路地奇偶分点,相邻两点连边(显然不能为 #)。 先求一个最大匹配。 …...

P1020 [NOIP1999 普及组] 导弹拦截
题目描述 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统…...

Makefile学习
什么是Makefile 使用 GCC 编译器在 Linux 进行 C 语言编译,通过在终端执行 gcc 命 令来完成 C 文件的编译,如果我们的工程只有一两个 C 文件还好,需要输入的命令不多,当文件有几十、上百甚至上万个的时候用终端输入 GCC 命令的方…...

2.4 随机变量函数的分布
学习目标: 学习随机变量函数的分布,我会采取以下步骤: 熟悉随机变量的基本概念和分布:在学习随机变量函数的分布之前,需要先掌握随机变量的基本概念和分布,包括离散型随机变量和连续性随机变量的概率密度…...

数据结构【一】:前缀表达式与后缀表达式的区别
在早期计息机系统中,由于没有括号规定运算顺序,因此,依靠出栈和入栈两种方式,限定元素和符号之间的关系确定了前缀表达式和后缀表达式两种运算方式,中缀表达式即为普通的运算表达式;注意,在栈结…...

搭建 PostgreSQL
端口:5432 代理备份端口:6432 下载 postgresql-15.0-1-windows-x64 乱码显示 配置环境变量 PGDATA数据目录位置 找到postgresql.conf文件, 修改参数 lc_messagesUTF8 max_connections 1000 shared_buffers4GB work_mem8MB 问题:…...

Nmap入门到高级【第四章】
预计更新Nmap基础知识 1.1 Nmap简介和历史 1.2 Nmap安装和使用方法 1.3 Nmap扫描技术和扫描选项 Nmap扫描技术 2.1 端口扫描技术 2.2 操作系统检测技术 2.3 服务和应用程序检测技术 2.4 漏洞检测技术 Nmap扫描选项 3.1 扫描类型选项 3.2 过滤器选项 3.3 探测选项 3.4 输出选项…...

c++正则表达式及其使用,超级详细
文章目录 概述正则表达式语法正则表达式操作std::regex_matchstd::regex_replacestd::regex_search 实例匹配邮箱替换 HTML 标签搜索 URL 总结 概述 正则表达式是一种用于匹配字符串的工具,可以在文本中查找特定的模式,并且可以快速地对字符串进行搜索和…...

【LeetCode: 剑指 Offer II 099. 最小路径之和 | 暴力递归 | DFS =>记忆化搜索=>动态规划】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...

Python OpenCV 计算机视觉:6~7
原文:OpenCV Computer Vision with Python 协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【ApacheCN 计算机视觉 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。 当别人说你没有底线的时候,你最…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
