【数据结构初阶】第七节.树和二叉树的性质
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
前言
一、树
1.1 树的概念
1.2 树的结点分类
1.3 结点之间的关系
1.4 树的存储结构
1.5 其他相关概念
二、 二叉树
2.1 二叉树的概念
2.2 特殊的二叉树
2.3 二叉树的性质
2.4 性质的相关习题
总结
前言
今天我们将进入到树与二叉树的相关内容当中,本节内容讲述了二叉树和树的有关性质和概念;
让我们一起进入到今天的学习当中吧!!!!!!!!!!
一、树
1.1 树的概念
这是现实世界的树

而我们这里所说的树,其实是一种特殊的数据结构
之前我们学习的不管是顺序表还是链表、队列、栈,都是一对一的线性结构。但在数据生活中还有很多一对多的情况,所有我们就要用到这种一对多的数据结构——树;

树(Tree)是n(n≥0)个结点的有限集。n=0时称为空树。
在任意一颗非空树中:
(1)有且仅有一个特定的称为根(root)的结点
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集 T 1 , T 2 , . . . , T m ;其中每一个集合本身又是一棵树,并且称为根的子树;
有两个点需要注意一下:
- 树是递归定义的——也就是说树的定义之中还用到了树的定义;
- 树形结构中,子树之间不能有交集,否则就不是树形结构;
解释一下这两点:
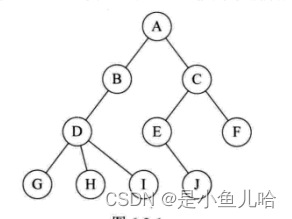
比如这是一个树
下图的子树T1和T2就是根结点A的子树。当然,D,G,H,I组成的树又是B为结点的子树,E、J、F组成的树是C为结点的树的子树。
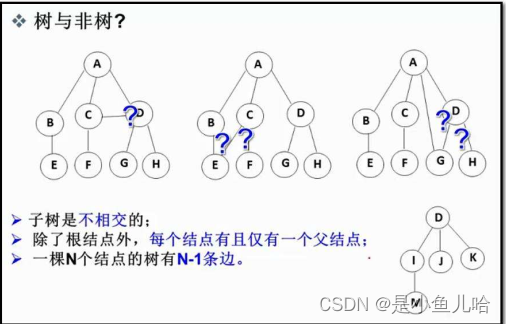
一些非树的例子 :
注:上面三个就不是树结构,只有右下角的那个称为树型结构;
1.2 树的结点分类
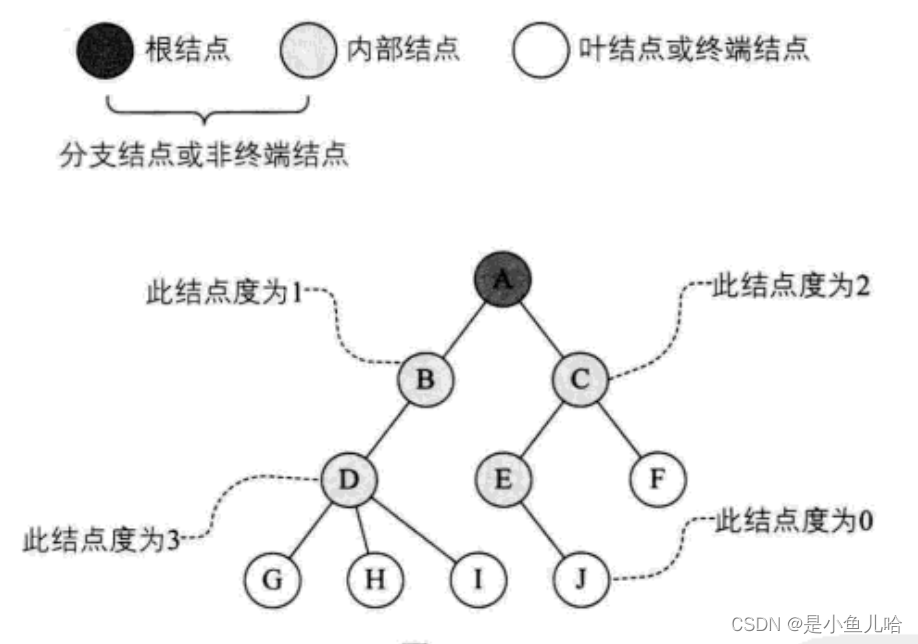
树的结点包含一个数据元素及若干指向其子树的分支;结点拥有的子树数称为结点的度(Degree) 。
度为0的结点称为叶结点(Leaf)或终端结点;度不为0的结点称为非终端结点或分支结点。除根结点之外,分支结点也称为内部结点。树的度是树内各结点的度的最大值。
如下图,因为这棵树结点的度的最大值是结点D的度,为3,所以树的度为3.
1.3 结点之间的关系
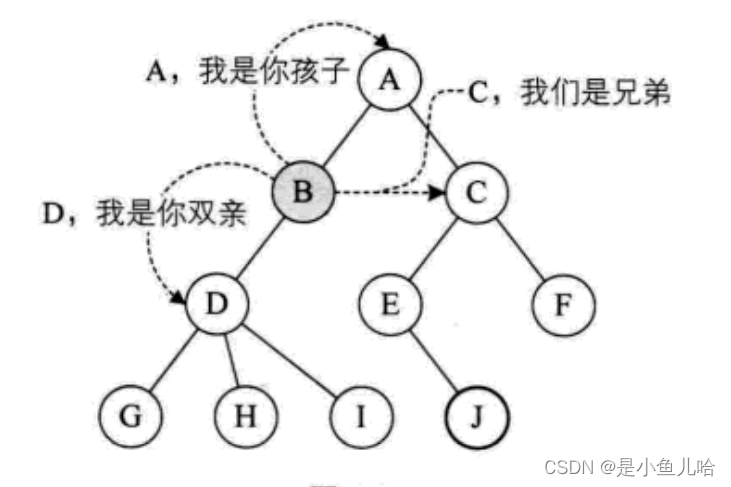
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
图示说明:
节点的祖先:从根到该节点所经分支上的所有节点。如上图对于结点H来说,D、B、A都是他的祖先;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:B的子孙有D、G、H、I;
1.4 树的存储结构
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
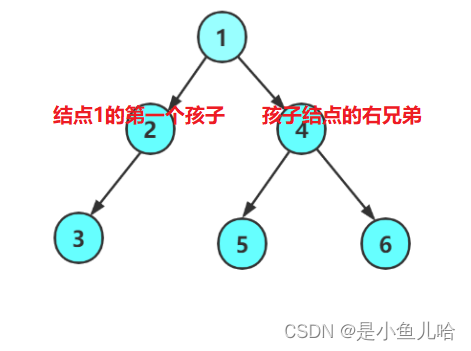
我们观察后发现,任意一棵树,它的结点的第一个孩子如果存在就是唯一的。因此,我们设置两个结点引用,分别指向该结点的第一个孩子和该结点的右兄弟。
结点结构如表所示:

代码分析:
class TreeNode {
int date; // 数据域
TreeNode firstchild; // 该结点的第一个孩子
TreeNode rightbrother; // 该结点的右兄弟
}
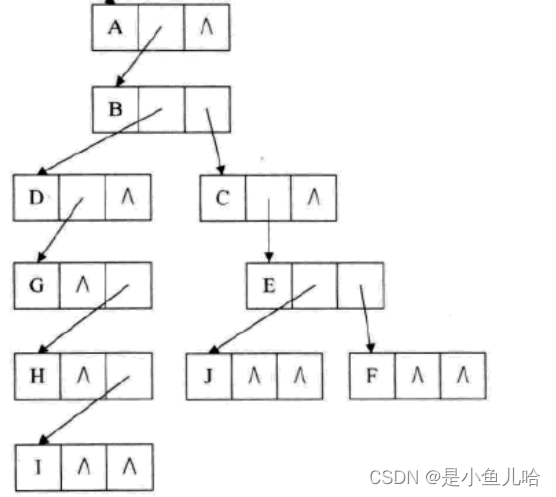
那么下面的树:

就可以表示成:

这种表示其实就是把一棵复杂的树变成了一棵二叉树 ;
至于二叉树是什么?这也是咱们接下来要重点聊的内容了;
1.5 其他相关概念
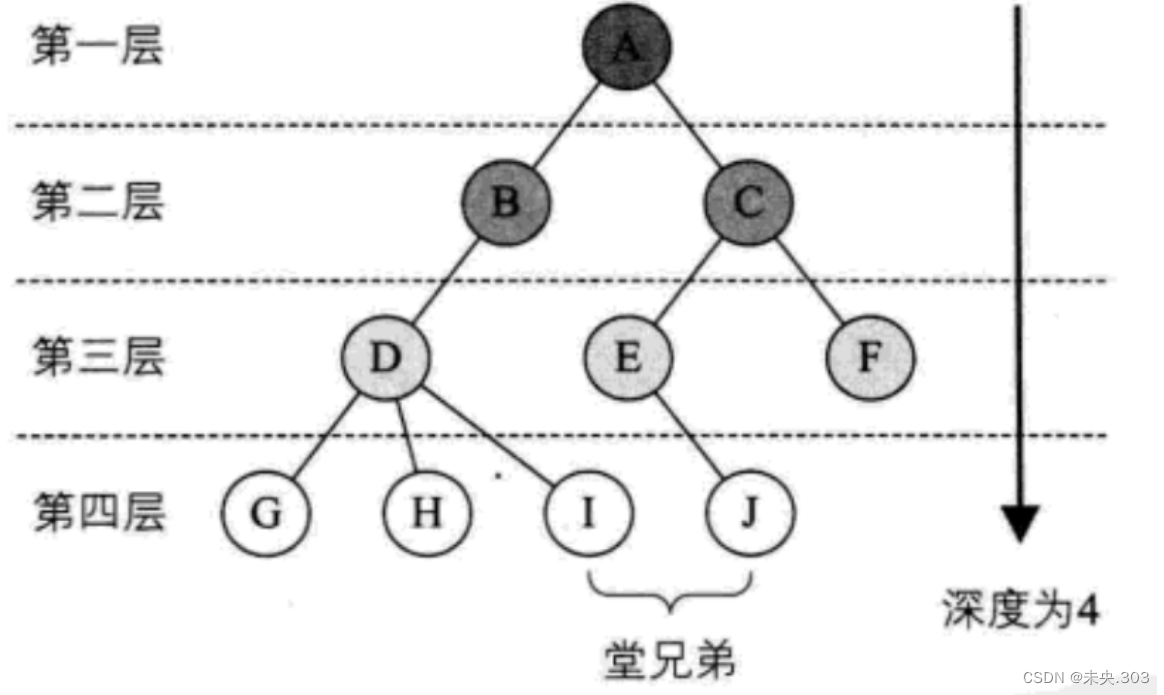
结点的层次:从一棵树的树根开始,树根所在层为第一层,根的孩子结点所在的层为第二层,依次类推;
树的高度或深度:树中节点的最大层次;
堂兄弟节点:双亲在同一层的节点互为堂兄弟;
堂兄弟节点图示解释:
森林:由m(m>0)棵互不相交的树的集合称为森林;
有序树和无序树:如果树中结点的子树从左到右看,谁在左边,谁在右边,是有规定的,这棵树称为有序树;反之称为无序树。
(在有序树中,一个结点最左边的子树称为"第一个孩子",最右边的称为"最后一个孩子"。)

二、 二叉树
2.1 二叉树的概念
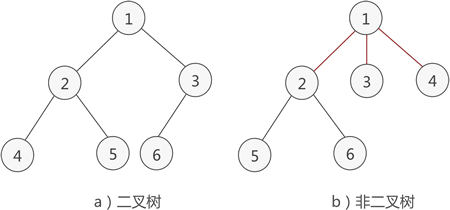
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
例如,图 1a) 就是一棵二叉树,而图 1b) 则不是。
再深入的理解就是:
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空;
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成;
图示举例:

从上图可以看出:
1. 二叉树不存在度大于2的结点;
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树;
注意:
对于任意的二叉树都是由以下几种情况复合而成的:
2.2 特殊的二叉树
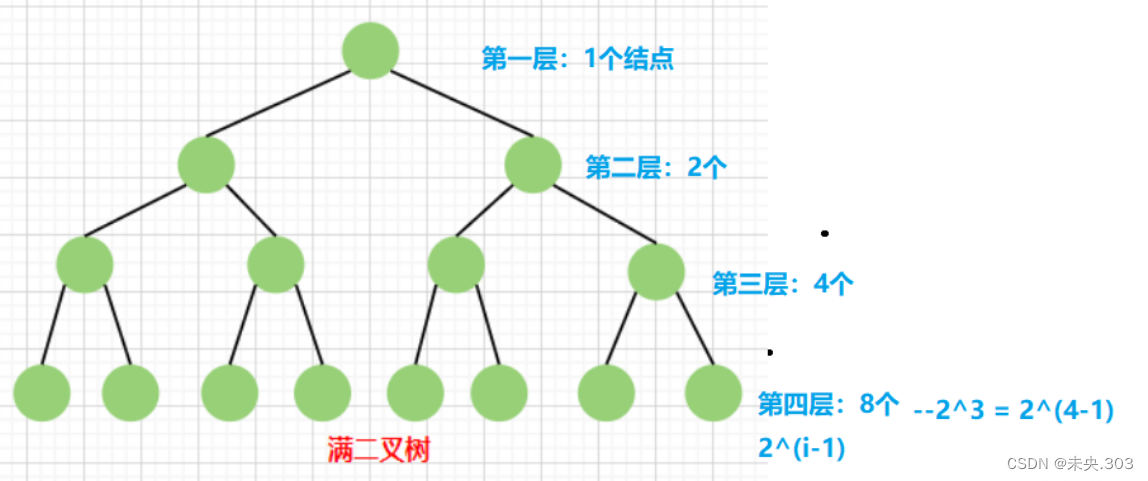
满二叉树:
如果二叉树中除了叶子结点,每个结点的度都为 2;

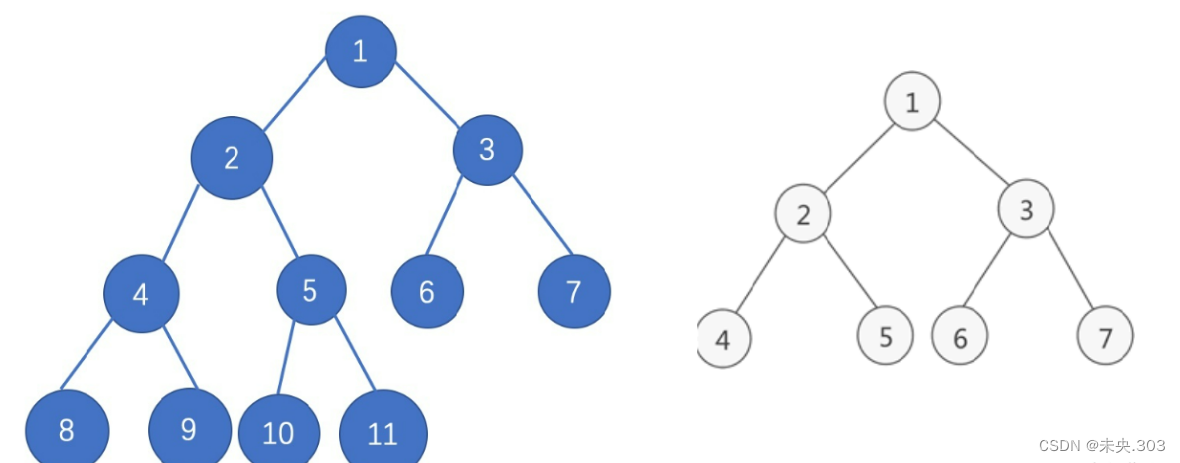
完全二叉树 :
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布;

如图 3a) 所示是一棵完全二叉树,图 3b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
其实完全二叉树类似这下面这种情况:
从中我们也可以发现一些规律,如果一个完全二叉树的某一个结点没有右子树,那么该结点一定没有左子树,有右子树就一定得有左子树。它从左到右一定是连续的,中间不能出现空的。
注意:
一个慢二叉树一定是一棵完全二叉树,但完全二叉树不一定是满二叉树。
2.3 二叉树的性质
性质一:若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
解析:
我们来观察下面的图形:
性质2:若规定根节点的层数为1,则深度为k的二叉树的最大结点数是2^k - 1 .(深度为k意思就是有k层的二叉树)
解析:
我们前面已经知道,一棵非空二叉树的第i层上2^(i-1) 个结点,那么k层的二叉树的结点树不就是首项是1、公比是2的等比数列求和吗?
性质3:对任何一棵非空二叉树, 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,则有n0 =n2 +1;
解析:
对于二叉树来说,我们会发现(除了根节点)对于每一个结点来说,都有其对应父结点分支指向它,假设树中分枝数为 B,那么总的结点数就是B+1;
设总结点数为n,度为0的结点(即叶子结点)个数为n0、度为1的结点个数为n1、度为2的结点个数为n2,那么就有n = n0 + n1 + n2;
同时分支数B = n1 + 2 * n2,B + 1 == n;
所以就有n0 = n2 + 1;
2.4 性质的相关习题
第一题:

解析:
该二叉树的结点数是奇数,而对于结点数是奇数的二叉树,像这样:
你会发现,该二叉树中度为1的结点数一个都没有,这不是偶然,你观察其他的的二叉树,会发现也有这样一个规律。
而对于结点数是偶数的二叉树呢?
你会发现结点数为偶数的二叉树,有且仅有一个度为1的结点;
综上所述:
那么这样我们就可以开始算了: 设叶子结点即——度为0的结点数为n0,度为1的结点数为n1(n1 == 0),度为2的结点数为n2(n2 = n0 -1);
即399 = n0 + n1 + n2 = 2* n0 - 1 --->n0 = 200;
第二题:
解析:
2n说明结点数是偶数个,度为1的结点个数为1,2n = n0 + n1 + n2 = 1 + n0 + (n0 - 1)
即n0 == n,叶子结点个数为n ;
第三题:

解析:
二叉树的性质:
非空二叉树的叶子结点等于双分支结点数加1;
第四题:

解析:
对于这个题目就要用到我们的性质四了;
2^9 == 512,即log2(531 + 1) == 9.xx,向上取整即为10,所以答案就是B;
性质四:具有n个结点的完全二叉树的深度k为 log2(n+1)上取整;
性质五:对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点;
2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子;
3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子;
总结
今天的内容就介绍到这里,下一句我们将继续介绍有关二叉树的编程的有关问题,以及二叉树的常见操作的使用等等;让我们下一期再见吧!!!!!!!!!!

相关文章:

【数据结构初阶】第七节.树和二叉树的性质
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 前言 一、树 1.1 树的概念 1.2 树的结点分类 1.3 结点之间的关系 1.4 树的存储结构 1.5 其他相关概念 二、 二叉树 2.1 二叉树的概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4…...

车载软件架构——闲聊几句AUTOSAR BSW(一)
我是穿拖鞋的汉子,魔都中坚持长期主义的工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 人生是用来体验的,不是用来演绎完美的。我慢慢能接受自己身上那些灰暗的部分,原谅自己的迟钝和平庸,允许自己出错,允许自己偶尔断电,带着缺憾拼命绽放,…...
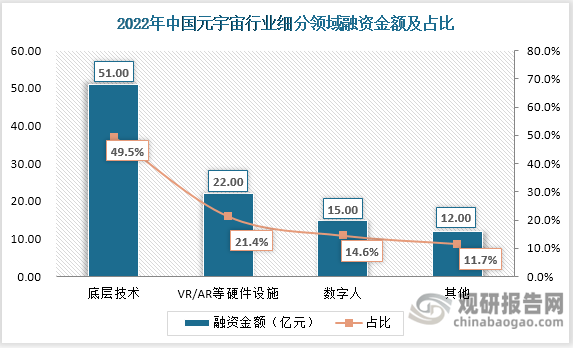
我国元宇宙行业分析:政策、技术、资金助推行业探索多元化应用场景
1.元宇宙行业概述、特征及产业链图解 元宇宙是人类运用数字技术构建的,由现实世界映射或超越现实世界,可与现实世界交互的虚拟世界,具备新型社会体系的数字生活空间,主要具有沉浸式体验、开放性、虚拟身份、不断演化、知识互动、…...

都已经那么卷了,用户还需要开源的 API 管理工具么
关于 API 管理工具,如今的市场已经把用户教育的差不多了,毫不夸张地说,如果我随机抽取一位幸运读者,他都能给我罗列出一二三四款大家耳熟能详的工具。可说到开源的 API 管理工具,大家又能知道多少呢? 我们是…...

工信部教育与考试中心-软件测试工程师考试题A卷-答
软件测试工程师考试题 姓名________________ 学号_________________ 班级__________________ 题号 一 二 三 四 五 总分 分数 说明:本试卷分五部分,全卷满分100分。考试用时100分钟。 注 意 事 项:1、本此考试为闭卷…...
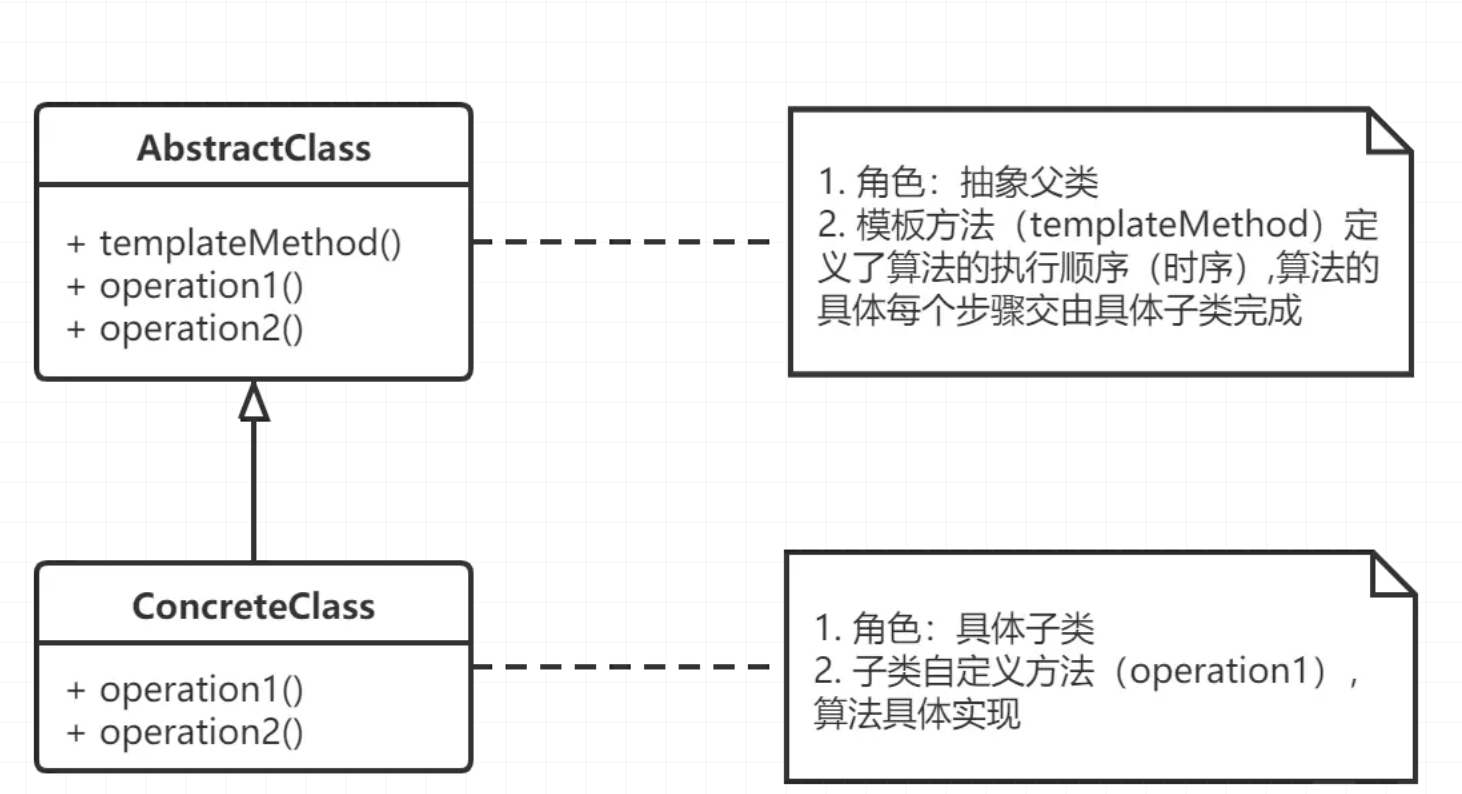
【设计模式】模板方法模式--让你的代码更具灵活性与可扩展性
文章目录 前言模板方法模式的定义核心组成模板方法模式与其他设计模式的区别 代码实现抽象类具体类Client 经典类图spring中的例子 总结 前言 在软件开发中,设计模式是一种经过实践检验的、可复用的解决方案,它们可以帮助我们解决某一特定领域的典型问题…...

搞明白Redis持久化机制
Redis是一种内存数据库,其内存中的数据存储在计算机的内存中,如果服务器发生崩溃或者重启,内存中的数据将会丢失。为了避免这种情况发生,Redis提供了两种持久化机制:RDB和AOF。 一、RDB持久化 Redis支持将当前数据状…...

C# 中的正则表达式,如何使用正则表达式进行字符串匹配和替换?
在 C# 中,可以使用正则表达式进行字符串匹配和替换。正则表达式是一种用来描述字符串模式的语言,可以用来检查一个字符串是否符合某种模式,或者从字符串中提取符合某种模式的子串。下面我们介绍一些常用的正则表达式操作: 创建正…...

7年时间,从功能测试到测试开发月薪30K,有志者事竟成
突破自己的技术瓶颈并不是一蹴而就,还是需要看清楚一些东西,这里也有一些经验和见解跟大家分享一下。同样是职场人士,我也有我的经历和故事。在工作期间,我有过2年加薪5次的小小“战绩”(同期进入公司的员工࿰…...
ES6 块级作用域
ES6之前没有块级作用域,ES5的var没有块级作用域的概念,只有function有作用域的概念,ES6的let、const引入了块级作用域。 ES5之前if和for都没有作用域,所以很多时候需要使用function的作用域,比如闭包。 1.1.1 什么…...

ShardingSphere-JDBC垂直分片
什么是数据分片? 简单来说,就是指通过某种特定的条件,将我们存放在同一个数据库中的数据分散存放到多个数据库(主机)上面,以达到分散单台设备负载的效果。 数据的切分(Sharding)根据…...

Node 04-http模块
HTTP 协议 概念 HTTP(hypertext transport protocol)协议;中文叫 超文本传输协议 是一种基于TCP/IP的应用层通信协议 这个协议详细规定了 浏览器 和 万维网 服务器 之间互相通信的规则 协议中主要规定了两个方面的内容: 客户端࿱…...
)
记录项目过程中的编译错误及解决方法(持续更新中)
文章目录 前言 前言 记录做项目的时候编译问题,好记性不如烂笔头,下次碰到相同的问题也可以方便查阅 2023.3.22 问题1:每次跑回归测试的时候,总是会出现错误,总共只有5个test,单独跑这个case的时候是没有…...

Android Hilt依赖注入框架
Hilt 是一个基于 Dagger2 的依赖注入框架,它提供了一些简便的注入方式来简化开发者在 Android 应用中使用 Dagger2 的复杂性。Hilt 旨在简化 Android 应用程序中的依赖注入实现,使开发人员能够更轻松地管理依赖项和应用程序的组件。 Hilt 的主要目标是提…...

LeetCode:59. 螺旋矩阵 II
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀 算法专栏: 👉🏻123 一、🌱59. 螺旋矩阵 II 题目描述:给你一个正整数 n ,…...

信息安全复习六:公开密钥密码学
一、章节梗概 1.公开密钥密码模型的基本原理 2.两个算法:RSA&D-H算法 主要内容 1.对称密钥密码的密钥交换问题 2.公钥密码模型的提出 3.设计公钥密码的基本要求 4.数字签名 5.RSA算法 6.公钥密码的特征总结 二、对称密钥密码 对称加密算法中,数据…...

YOLOv8 更换主干网络之 ShuffleNetv2
《ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design》 目前,神经网络架构设计多以计算复杂度的间接度量——FLOPs为指导。然而,直接的度量,如速度,也取决于其他因素,如内存访问成本和平台特性。因此,这项工作建议评估目标平台上的直接度量,而…...

async/await最详细的讲解
一、async 和 await 在干什么 async 是“异步”的简写,而 await 的意思是等待。async 用于申明一个 function 是异步的,而 await 等待某个操作完成。 async/await 是一种编写异步代码的新方法。之前异步代码的方案是回调和 promise。 async/await 像 p…...

学习数据结构第6天(栈的基本概念)
栈的基本概念 栈的定义栈的基本操作栈的存储结构 栈的定义 栈(Stack)是一种基于先进后出(FILO)或者后进先出(LIFO)的数据结构,是一种只允许在一端进行插入和删除操作的特殊线性表。 栈按照先进后出的原则存储数据,先进入的数据被压入栈底,最…...

自动化添加时间戳版本号
自动化添加时间戳版本号 前言一、静态资源二、版本号的来源三. 版本信息的位置四. 添加时间戳版本号1. 手动添加2. 自动化生成 前言 软件开发和发布过程中,版本是个极其重要的因素。大至操作系统,小到功能组件,都会涉及到版本相关的问题。 …...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...