滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样，是很多机械设备上不可或缺的重要部件，它是确保机器能够具备高加工精度的前提条件，因此本身对于精度的要求也相当地高。今天，我们就来了解一下滚珠螺杆在不同设备上的应用吧！
1、大型的加工中心，通常大型的加工中心工具机的转速是相当高的，因此这种综合性比较强且速度比较快的机械设备，需要配套使用那种DN值比较高的滚珠螺杆，能够承受运行中巨大的负载。
2、一般的自动化机械，对于负载方面的要求并不是很高，一般的端盖式滚珠螺杆就能够满足这种使用条件的要求。
3、电子机械、CNC机械和精密工具机，这些设备不仅要求有较高的加工精度，并且在灵活性方面也有相当高的要求，因此在这种使用场合中，需要滚珠螺杆能够达到高速运转的需求。
4、精密电子，在电子电器行业也会用到滚珠螺杆，这类行业少不了对于机器人的应用，还有部分半导体机械上也需要使用滚珠螺杆，对于这类机械，螺帽旋转式滚珠螺杆能够满足调节不同精度的需求。
5、小型加工机械，在小型加工机械上运用的滚珠螺杆，不需要多高的加工精度，并且小型的加工机械的体积小，通常使用较为小型的滚珠螺杆。
那么在哪些领域上用的上他们呢？
1、自动化设备：需要精确的定位和控制的自动化生产线、自动化包装线、自动化搬运设备等这些，滚珠螺杆能够提供高精度和高重复性的运动控制，从而保证设备的工作精度和稳定性。
2、机器人：滚珠螺杆在机器人关节的驱动中具有重要的作用。机器人关节需要进行精确的角度调节和定位，而滚珠螺杆能够提供高精度和高重复性的运动控制，保证机器人的动作精度和稳定性。
3、飞行器：需要进行精确的定位和控制的卫星、导弹等这些飞行器，滚珠螺杆能够提供高精度和高重复性的运动控制，从而保证飞行器的精确定位和稳定性。
4、医疗设备：广泛应用在CT机、核磁共振设备等这些医疗设备中，这些设备需要进行高精度的位置控制和运动控制，滚珠螺杆能够提供精确的运动控制，保证医疗设备的精度和可靠性。
以上就是一些关于滚珠螺杆在不同设备上的应用内容，希望可以帮助大家进一步了解滚珠螺杆。
相关文章：
滚珠螺杆在设备上的应用
滚珠螺杆跟直线导轨一样，是很多机械设备上不可或缺的重要部件，它是确保机器能够具备高加工精度的前提条件，因此本身对于精度的要求也相当地高。今天，我们就来了解一下滚珠螺杆在不同设备上的应用吧！ 1、大型的加工中心…...
Day41线程同步
线程同步 案例：三个窗口卖100张票 //定义一个类SellTicket实现Runnable接口，定义成员变量100张票 public class SellTicket implements Runnable{private int tickets 100;//重写run方法Overridepublic void run(){while (true){ //没有票后&…...
设计模式之享元模式
参考资料 曾探《JavaScript设计模式与开发实践》；「设计模式 JavaScript 描述」享元模式设计模式之享元模式Javascript 设计模式 - 享元模式 定义 享元模式的英文叫：Flyweight Design Pattern。享元设计模式是用于性能优化的模式，这种设计…...
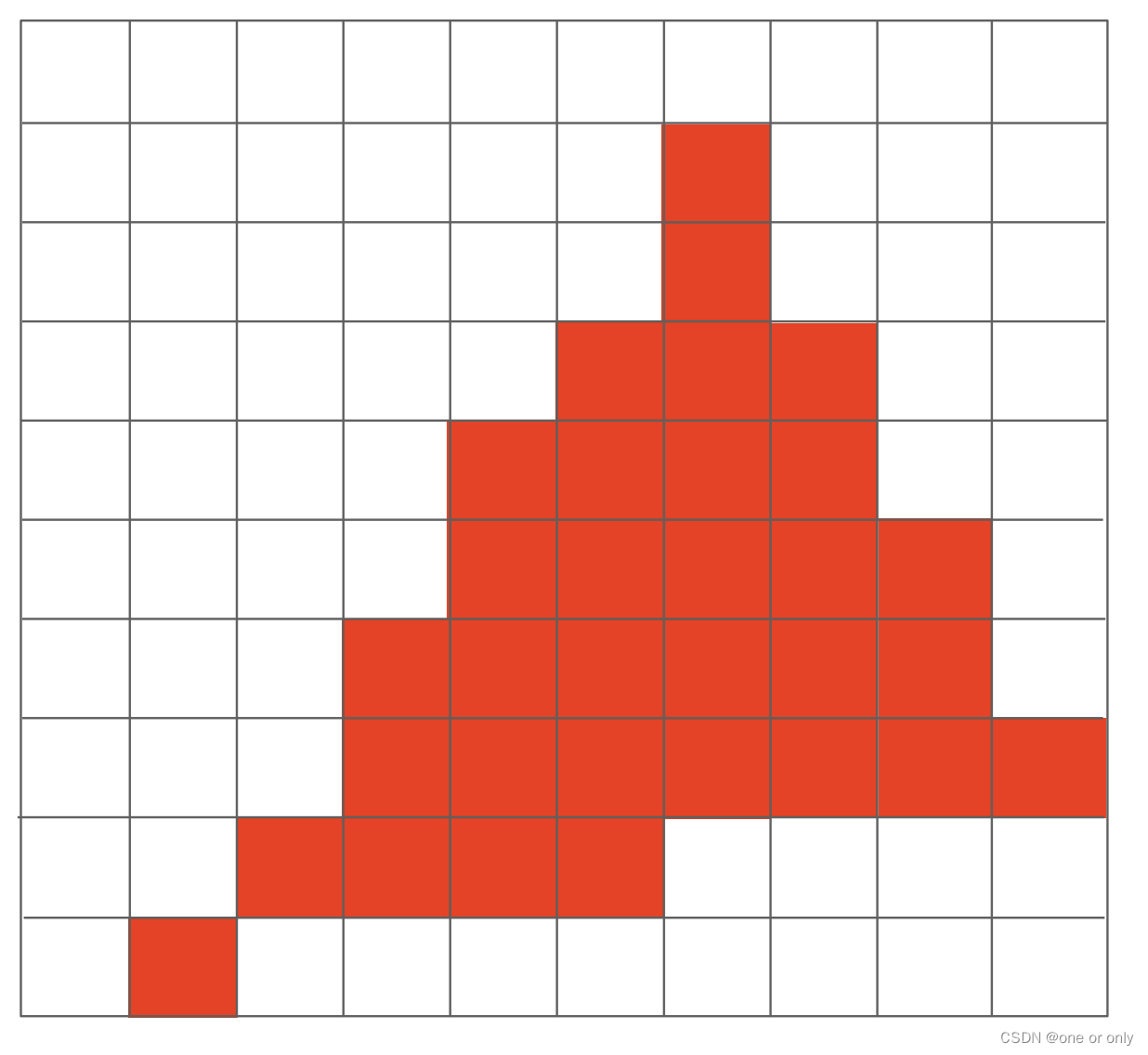
【GAMES101】05 Rasterization（Triangles）
光栅化过程：将一系列变换后的三角形转换为像素的过程。 三角形在图形学中得到很多的应用。 最基础的多边形（边数最少）。任何多边形都可以拆成三角形。性质：三角形内部一定是平面的。三角形内外部定义非常清楚。定义三个顶点后&a…...
13. Pod 从入门到深入理解（二）
本章讲解知识点 Pod 容器共享 VolumeConfigMapSecretDownward APIEmptyDir VolumeHostPath Volume1. Pod 容器共享 Volume 1.1. Volume 的背景及需要解决的问题 存储是必不可少的，对于服务运行产生的日志、数据，必须有一个地方进行保存，但是我们的容器每一次重启都是“恢复…...
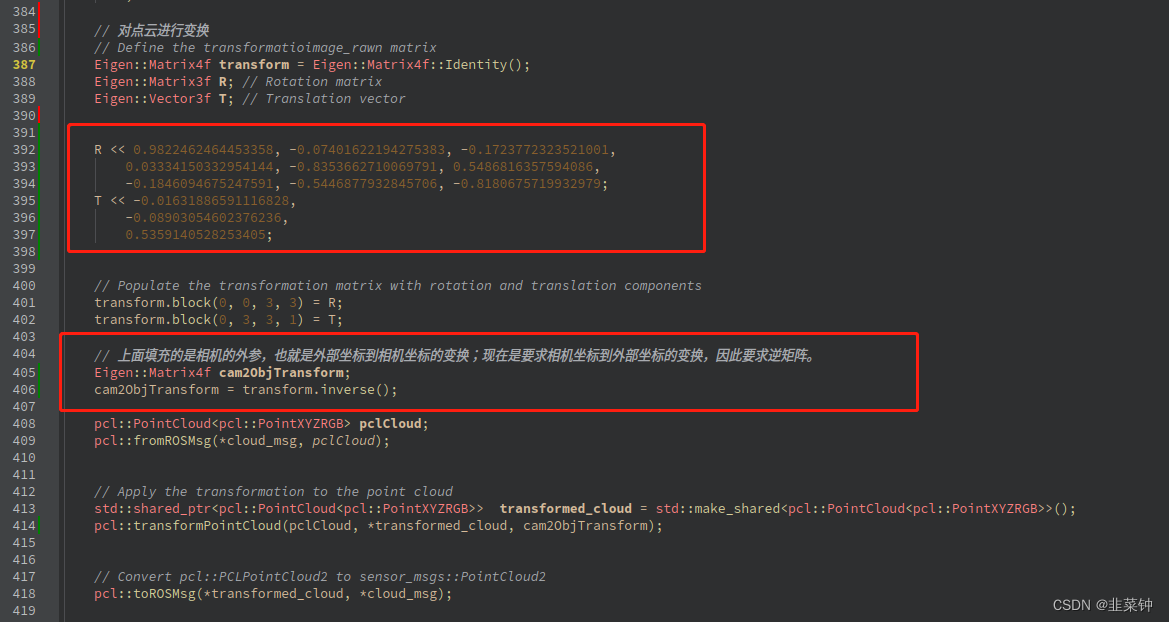
ORBBEC（奥比中光）AstraPro相机在ROS2下的标定与D2C（标定与配准）
文章目录 1.rgb、depth相机标定矫正1.1.标定rgb相机1.2.标定depth相机1.3.rgb、depth相机一起标定（效果重复了，但是推荐使用）1.4.取得标定结果1.4.1.得到的标定结果的意义 1.5.IR、RGB相机分别应用标定结果1.5.1.openCV应用标定结果1.5.2.ros…...
常量与变量：编程中重要的两种数据类型
常量与变量 在编程中，我们常常需要存储一些数据。这些数据有些是恒定不变的，有些却是可以随时变化的。对于恒定不变的数据，我们称之为常量；对于可以变化的数据，我们则称之为变量。这两种数据类型在程序中非常重要&…...
( 数组和矩阵) 287. 寻找重复数 ——【Leetcode每日一题】
❓287. 寻找重复数 难度：中等 给定一个包含 n 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。 假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。 你…...
【学习笔记】「JOISC 2022 Day2」复制粘贴 3
看了正解。我觉得很厉害。虽然用减枝水过去了。 区间 d p dp dp。但是这个转移怎么看都不是 O ( 1 ) O(1) O(1)的。 border \text{border} border 那么 trick \text{trick} trick应该都能看出来。能进行剪切操作当且仅当 s [ l , p ] s [ q , r ] s_{[l,p]}s_{[q,r]} s[l,p]…...
武忠祥老师每日一题||定积分基础训练（三）
常用的基本不等式： sin x < x < t a n x , x ∈ ( 0 , π 2 ) \sin x<x<\ tan x,x\in(0,\frac{\pi}{2}) sinx<x< tanx,x∈(0,2π) e x ≥ 1 x , x ∈ ( − ∞ , ∞ ) e^x\ge1x,x\in(-\infty,\infty) ex≥1x,x∈(−∞,∞) x 1 x ≤ ln …...
Docker安装常用软件-Apollo（有问题）
零：apollo概念介绍 官网网站：GitHub - apolloconfig/apollo: Apollo is a reliable configuration management system suitable for microservice configuration management scenarios. gitee网址：mirrors / ctripcorp / apollo GitCode …...
f(x)与|f(x)|，f ‘ (x)，F(x)常见关系。
1.f(x)与|f(x)|关系。 1.连续关系。(f(x)在"[a,b]上连续" > |f(x)|在"[a,b]连续") ①如果f(x)在[a,b]上连续。则|f(x)|在[a,b]上连续. （因为f(x)在x0的连续点>x0必为|f(x)|的连续点） 注：”[a,b]连续“包括&#…...
今天面了一个来字节要求月薪23K，明显感觉他背了很多面试题...
最近有朋友去字节面试，面试前后进行了20天左右，包含4轮电话面试、1轮笔试、1轮主管视频面试、1轮hr视频面试。 据他所说，80%的人都会栽在第一轮面试，要不是他面试前做足准备，估计都坚持不完后面几轮面试。 其实&…...
如何使用二元三次回归分析建立预测模型？（分析、原理、代码示例）
二元三次回归是一种用于建立两个自变量与一个因变量之间关系的回归模型，常用于数据分析和预测。下面我会更详细地解释一下二元三次回归的原理、分析和示例代码。 1、原理 二元三次回归分析用多项式回归建立预测模型，其中包括两个自变量（通常…...
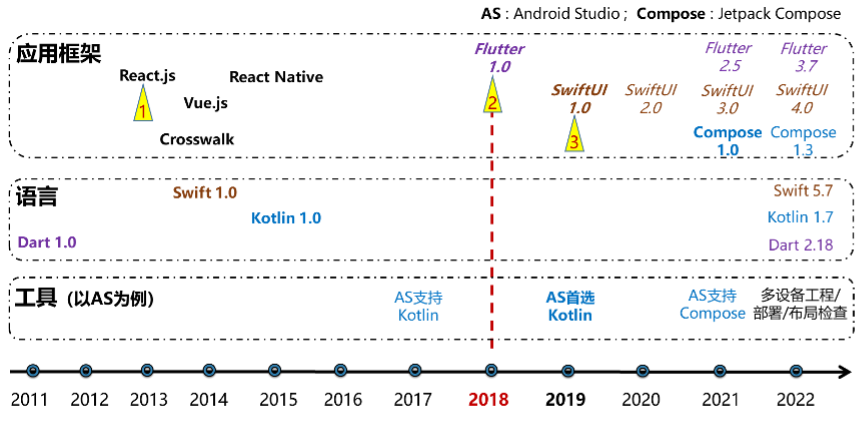
面向万物智联的应用框架的思考和探索（上）
原文：面向万物智联的应用框架的思考和探索（上），点击链接查看更多技术内容。 应用框架，是操作系统连接开发者生态，实现用户体验的关键基础设施。其中，开发效率和运行体验是永恒的诉求，…...
《Python机器学习基础教程》第1章学习笔记
目录 第1章 引言 1.1 为何选择机器学习 1.1.1 机器学习能够解决的问题 第1章 引言 机器学习又称为预测分析或统计学习，是一个交叉学科，是从数据中提取知识。 1.1 为何选择机器学习 智能应用早期，使用专家设计的规则体系来设计。 缺点&…...
ClickHouse 内存管理是如何实现的
概述 本文介绍Clickhouse内存管理的实现原理。通过本文的分析，可以对Clickhouse的内存管理有一个概要的理解。 Clickouse内存管理组成 ClickHouse 使用内存管理系统来控制内存资源的分配和释放。内存管理系统的主要组成部分是： 内存池：Cl…...
docker容器技术
什么是docker Docker 使用 Google 公司推出的 Go 语言 进行开发实现，基于 Linux 内核的 cgroup，namespace，以及 OverlayFS 类的 Union FS 等技术，对进程进行封装隔离，属于 操作系统层面的虚拟化技术。由于隔离的进程独…...
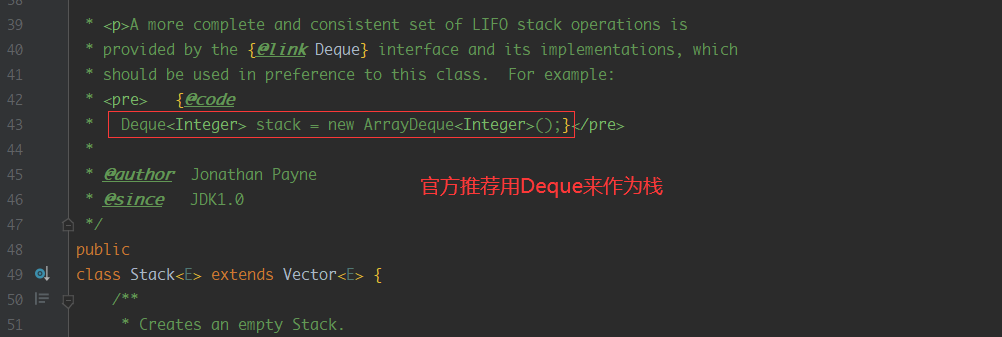
设计模式七大设计原则
文章目录 1、什么是设计模式2、单一职责原则3、开闭原则4、接口隔离原则5、依赖倒置原则6、迪米特法则（最少知道原则）7、里式替换原则8、组合优于继承 设计模式主要是为了满足一个字 变，这个字，可能是需求变更、可能是场景变更&a…...
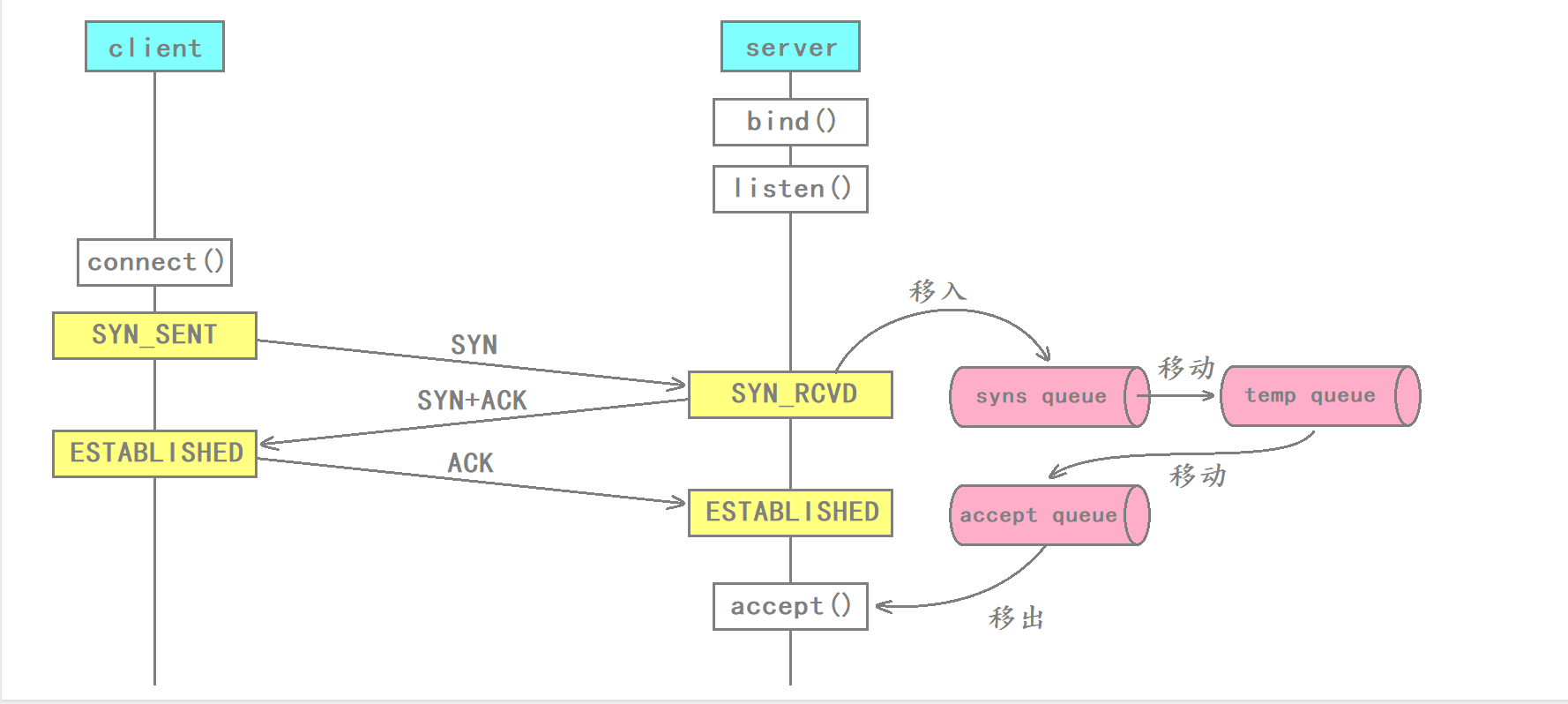
【Hello Network】TCP协议相关理解
作者：小萌新 专栏：网络 作者简介：大二学生 希望能和大家一起进步 本篇博客简介：补充下对于TCP协议的各种理解 TCP协议相关实验 TCP相关试验理解CLOSE_WAIT状态理解TIME_WAIT状态解决TIME_WAIT状态引起的bind失败的方法理解listen的…...
调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候，遇到了一些问题，记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合
强化学习（Reinforcement Learning, RL）是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程，然后使用强化学习的Actor-Critic机制（中文译作“知行互动”机制），逐步迭代求解…...
Cesium1.95中高性能加载1500个点
一、基本方式： 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名（Class Name)2.协议名（Protocol Name)3.方法名（Method Name)4.属性名（Property Name）5.局部变量/实例变量（Local / Instance Variables&…...
django filter 统计数量 按属性去重
在Django中，如果你想要根据某个属性对查询集进行去重并统计数量，你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求： 方法1：使用annotate()和Count 假设你有一个模型Item，并且你想…...
1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件，然后打开终端，进入下载文件夹，键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
C++.OpenGL （10/64）基础光照（Basic Lighting）
基础光照（Basic Lighting） 冯氏光照模型（Phong Lighting Model） #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
C# SqlSugar：依赖注入与仓储模式实践
C# SqlSugar：依赖注入与仓储模式实践 在 C# 的应用开发中，数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护，许多开发者会选择成熟的 ORM（对象关系映射）框架，SqlSugar 就是其中备受…...
是否存在路径（FIFOBB算法）
题目描述 一个具有 n 个顶点e条边的无向图，该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序，确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数，分别表示n 和 e 的值（1…...