转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录
- 1. 转换矩阵、平移矩阵、旋转矩阵之间的关系
- 2. 缩放变换、平移变换和旋转变换
- 2. python实现旋转矩阵、四元数、欧拉角互相转化
由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄明白之后干脆写一篇文章,给人方便同时于己方便,后续如有扩充或变动也方便添加。
1. 转换矩阵、平移矩阵、旋转矩阵之间的关系
假设有两个向量a1=(x1,y1,z1)a_1 = (x_1, y_1, z_1)a1=(x1,y1,z1)和a2=(x2,y2,z2)a_2 = (x_2, y_2, z_2)a2=(x2,y2,z2),它们的转换关系为:
a1=R∗a2+Ta_1 = R * a_2 + T a1=R∗a2+T
这里RRR就是它的旋转矩阵,TTT就是它的平移矩阵。使用齐次方式表示如下:
(a11)=(RT01)∗(a21)\begin{pmatrix} a_1\\ 1 \end{pmatrix}= \begin{pmatrix} R&T\\ 0&1 \end{pmatrix}* \begin{pmatrix} a_2\\1 \end{pmatrix} (a11)=(R0T1)∗(a21)
使用元素值替换后,表示如下:
(x1y1z11)=(r11r12r13t1r21r22r23t2r31r32r33t30001)∗(x2y3z21)\begin{pmatrix} x_1\\y_1\\z_1\\1 \end{pmatrix}= \begin{pmatrix} r_{11}&r_{12}&r_{13}&t_{1}\\ r_{21}&r_{22}&r_{23}&t_{2}\\ r_{31}&r_{32}&r_{33}&t_{3}\\ 0&0&0&1 \end{pmatrix}* \begin{pmatrix} x_2\\y_3\\z_2\\1 \end{pmatrix} x1y1z11=r11r21r310r12r22r320r13r23r330t1t2t31∗x2y3z21
在仿射变换中的转换矩阵表示先线性变换再平移。在这里转换矩阵表示如下:
转换矩阵=(r11r12r13t1r21r22r23t2r31r32r33t30001)转换矩阵= \begin{pmatrix} r_{11}&r_{12}&r_{13}&t_{1}\\ r_{21}&r_{22}&r_{23}&t_{2}\\ r_{31}&r_{32}&r_{33}&t_{3}\\ 0&0&0&1 \end{pmatrix} 转换矩阵=r11r21r310r12r22r320r13r23r330t1t2t31
平移矩阵表示如下:
平移矩阵T=(t1t2t3)平移矩阵T=\begin{pmatrix} t_{1}\\ t_{2}\\ t_{3}\\ \end{pmatrix} 平移矩阵T=t1t2t3
旋转矩阵表示如下:
旋转矩阵R=(r11r12r13r21r22r23r31r32r33)旋转矩阵R=\begin{pmatrix} r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33} \end{pmatrix} 旋转矩阵R=r11r21r31r12r22r32r13r23r33
2. 缩放变换、平移变换和旋转变换
如果理解以上知识点之后,缩放变换、平移变换和旋转变换的特殊情况也迎刃而解。
- 缩放变换
缩放变换只是在尺度上进行改变,所以它的变换形式如下:
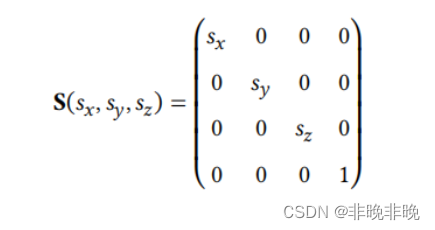
- 平移变换
平移变换的时候,角度不发生改变,也就是旋转矩阵R为单位矩阵,所以它的变换形式如下:
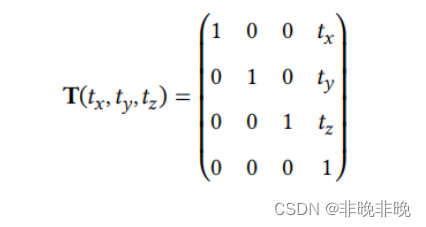
- 旋转变换
当空间内的物体绕着 x 轴,y 轴或者 z 轴旋转的时候,变换矩阵为:

对于一般性的旋转问题,可以用简单的旋转描述复杂的旋转。用 x 轴,y 轴和 z 轴上的旋转来定义旋转:
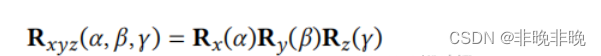
这三个角就被称作欧拉角(Euler angles)。
- 一目了然
- 这个也不错
2. python实现旋转矩阵、四元数、欧拉角互相转化
在应用中,我们往往会遇到旋转矩阵、四元数和欧拉角之间的互相转换,在这里,我们只使用python代码来实现它们之间互相转换。
from scipy.spatial.transform import Rotation as Rdef quaternion2euler(quaternion):r = R.from_quat(quaternion)euler = r.as_euler('xyz', degrees=True)return eulerdef euler2quaternion(euler):r = R.from_euler('xyz', euler, degrees=True)quaternion = r.as_quat()return quaterniondef euler2rotation(euler):r = R.from_euler('xyz', euler, degrees=True)rotation_matrix = r.as_matrix()return rotation_matrixdef quaternion2rotation_matrix(quaternion):r = R.from_quat(quaternion)rotation_matrix = r.as_matrix()return rotation_matrixdef rotation_matrix2euler(rotation_matrix):r = R.from_matrix(rotation_matrix)euler = r.as_euler('xyz', degrees=True)return eulerdef rotation_matrix2quaternion(rotation_matrix):r = R.from_matrix(rotation_matrix)quaternion = r.as_quat()return quaternionif __name__ == '__main__':# 四元数=>欧拉角quaternion = [0.71934025092983234, -1.876085535681999e-06, -3.274841213980097e-08, -0.69465790385533299]euler = quaternion2euler(quaternion) # [-9.20000743e+01 1.52039496e-04 -1.52039496e-04]print(f'euler: {euler}')# 四元数=>旋转矩阵rotation_matrix = quaternion2rotation_matrix(quaternion)print(f'rotation_matrix: {rotation_matrix}')# 欧拉角=>四元数quaternion = euler2quaternion(euler)print(f'quaternion: {quaternion}') # [-7.19340251e-01 1.87608554e-06 3.27484122e-08 6.94657904e-01]# 欧拉角=>旋转矩阵rotation_matrix = euler2rotation(euler)print(f'rotation_matrix: {rotation_matrix}')# 旋转矩阵=>欧拉角euler = rotation_matrix2euler(rotation_matrix)print(f'euler: {euler}')# 旋转矩阵=>四元数quaternion = rotation_matrix2quaternion(rotation_matrix)print(f'quaternion: {quaternion}')
相关文章:
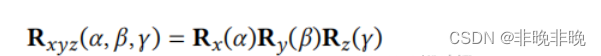
转换矩阵、平移矩阵、旋转矩阵关系以及python实现旋转矩阵、四元数、欧拉角之间转换
文章目录1. 转换矩阵、平移矩阵、旋转矩阵之间的关系2. 缩放变换、平移变换和旋转变换2. python实现旋转矩阵、四元数、欧拉角互相转化由于在平时总是或多或少的遇到平移旋转的问题,每次都是现查资料,然后查了忘,忘了继续查,这次弄…...
中国地图航线图(echarjs)
1、以上为效果图 需要jq、echarjs、china.json三个文件支持。以上 2、具体代码 DOM部分 <!-- 服务范围 GO--> <div class"m-maps"><div id"main" style"width:1400px;height: 800px; margin: 0 auto;"> </div> <!-…...
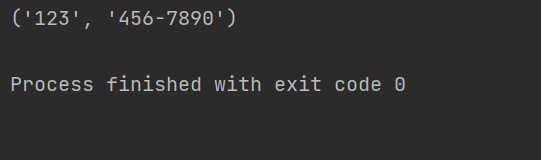
Python正则表达式中group与groups的用法详解
本文主要介绍了Python正则表达式中group与groups的用法详解,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧目录在Python中,正则表达式的group和groups方…...

c++练习题7
1.下列运算符中优先级最高的是 A)> B) C) && D)! 2.以下关于运算符优先级的描述中,正确的是 。 A)!(逻辑非&#x…...

MySQL学习
目录1、数据库定义基本语句(1)数据库操作(2)数据表操作2.数据库操作SQL语句(1)插入数据(2)更新语句(3)删除数据3.数据库查询语句(1)基…...

C语言(强制类型转换)
一.类型转换原则 1.升级:当类型转换出现在表达式时,无论时unsigned还是signed的char和short都会被自动转换成int,如有必要会被转换成unsigned int(如果short与int的大小相同,unsigned short就比int大。这种情况下,uns…...

搭建hadoop高可用集群(二)
搭建hadoop高可用集群(一)配置hadoophadoop-env.shworkerscore-site.xmlhdfs-site.xmlmapred-site.xmlyarn-site.xml/etc/profile拷贝集群首次启动1、先启动zk集群(自动化脚本)2、在hadoop151,hadoop152,hadoop153启动JournalNode…...

CentOS升级内核-- CentOS9 Stream/CentOS8 Stream/CentOS7
官方文档在此 升级原因 当我们安装一些软件(对,我说的就是Kubernetes),可能需要新内核的支持,而CentOS又比较保守,不太升级,所以需要我们手工升级. # 看下目前是什么版本内核 uname -a# 安装公钥 rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org# 添加仓库,如果…...
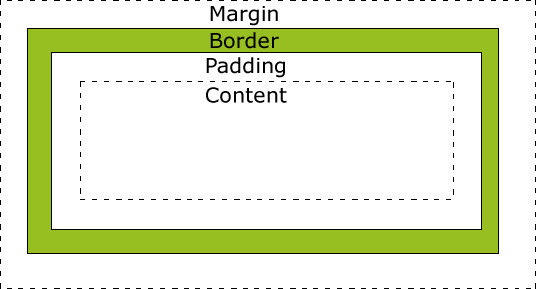
【基础篇】一文掌握css的盒子模型(margin、padding)
1、CSS 盒子模型(Box Model) 所有HTML元素可以看作盒子,在CSS中,"box model"这一术语是用来设计和布局时使用。CSS盒模型本质上是一个盒子,封装周围的HTML元素,它包括:边距,边框,填充,和实际内容。盒模型允许我们在其它元素和周围元素边框之间的空间放置元素…...
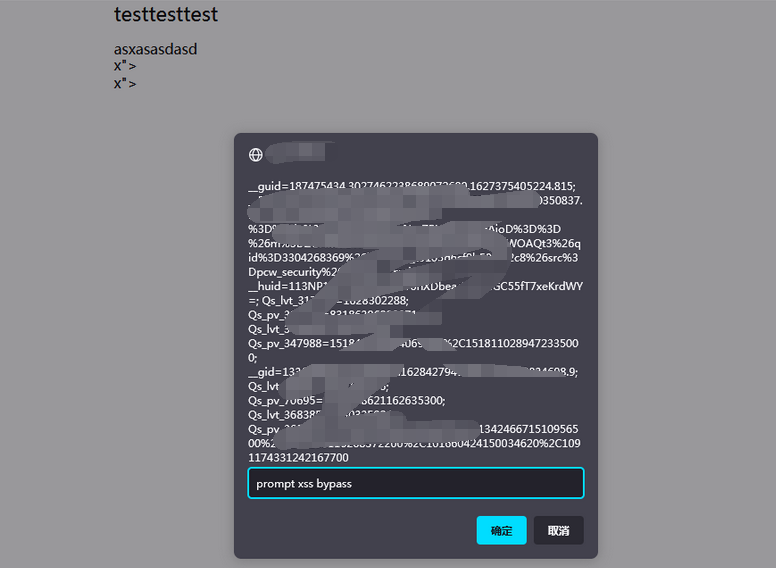
重生之我是赏金猎人-漏洞挖掘(十一)-某SRC储存XSS多次BypassWAF挖掘
0x01:利用编辑器的超链接组件导致存储XSS 鄙人太菜了,没啥高质量的洞呀,随便水一篇文章吧。 在月黑风高的夜晚,某骇客喊我起床挖洞,偷瞄了一下发现平台正好出活动了,想着小牛试刀吧 首先信息收集了一下&a…...

Wails简介
https://wails.io/zh-Hans/docs/introduction 简介 Wails 是一个可让您使用 Go 和 Web 技术编写桌面应用的项目。 将它看作为 Go 的快并且轻量的 Electron 替代品。 您可以使用 Go 的灵活性和强大功能,结合丰富的现代前端,轻松的构建应用程序。 功能…...
)
滑动窗口 AcWing (JAVA)
给定一个大小为 n≤10^6 的数组。 有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。 你只能在窗口中看到 k 个数字。 每次滑动窗口向右移动一个位置。 以下是一个例子: 该数组为 [1 3 -1 -3 5 3 6 7],k 为 33。 窗口位置最小值最大…...
vue小案例
vue小案例 组件化编码流程 1.拆分静态组件,按功能点拆分 2.实现动态组件 3.实现交互 文章目录vue小案例组件化编码流程1.父组件给子组件传值2.通过APP组件给子组件传值。3.案例实现4.项目小细节1.父组件给子组件传值 父组件给子组件传值 1.在父组件中写好要传的值&a…...

阅读笔记3——空洞卷积
空洞卷积 1. 背景 空洞卷积(Dilated Convolution)最初是为解决图像分割的问题而提出的。常见的图像分割算法通常使用池化层来增大感受野,同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图先缩小再放大的过程造成了精…...
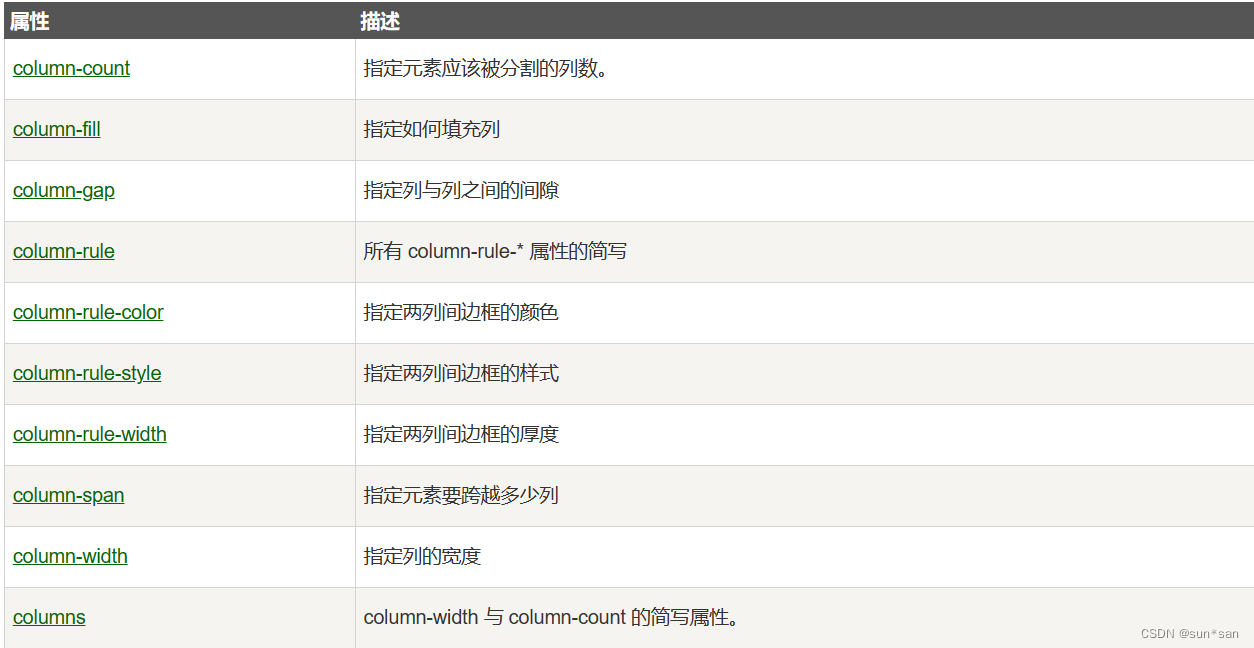
CSS系统学习总结
目录 CSS边框 CSS背景 CSS3渐变 线性渐变(Linear Gradients)- 向下/向上/向左/向右/对角方向 语法 线性渐变(从上到下) 线性渐变(从左到右) 线性渐变(对角) 使用角度 使用多…...

阿里一面:你做过哪些代码优化?来一个人人可以用的极品案例
前言 在尼恩读者50交流群中,尼恩经常指导小伙伴改简历。 改简历所涉及的一个要点是: 在 XXX 项目中,完成了 XXX 模块的代码优化 另外,在面试的过程中,面试官也常常喜欢针对提问,来考察候选人对代码质量的追…...
Android NFC 标签读写Demo与历史漏洞概述
文章目录前言NFC基础1.1 RFID区别1.2 工作模式1.3 日常应用NFC标签2.1 标签应用2.2 应用实践2.3 标签预览2.4 前台调度NFC开发3.1 NDEF数据3.2 标签的调度3.3 读写Demo3.4 Demo演示历史漏洞4.1 中继攻击4.2 预览伪造4.3 篡改卡片4.4 其它漏洞总结前言 NFC 作为 Android 手机一…...

亿级高并发电商项目-- 实战篇 --万达商城项目 六(编写角色管理、用户权限(Spring Security认证授权)、管理员管理等模块)
专栏:高并发---前后端分布式 👏作者简介:大家好,我是小童,Java开发工程师,CSDN博客博主,Java领域新星创作者 📕系列专栏:前端、Java、Java中间件大全、微信小程序、微信…...

博视像元获近5000万元融资,主攻半导体前道及锂电高端部件供应
这两年各大车企与电池厂商都在快速新建产能,尤其上游原材料成本大增,反映到产业链上巨头都在寻求增效,高端制造技术投入也大幅增长。比如这家,高端工业相机提供商「博视像元」近期宣布完成近5000万的天使加轮融资,投资…...

SpringCloud-断路器Hystrix
一、降级使用1、添加依赖<!--hystrix--><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-hystrix</artifactId></dependency>2、启动类添加注解EnableCircuitBreakerSpringBoot…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
