C++虚假唤醒
概念:
虚假唤醒是指在使用条件变量时,线程被唤醒但条件并没有满足,导致线程执行错误的情况,这个过程就是虚假唤醒。
虚假唤醒弊端:
- 虚假唤醒会导致程序的正确性受到影响,因为唤醒的线程并没有满足条件,可能会导致数据的丢失或者重复处理;可能会导致线程陷入死循环或执行错误。
- 虚假唤醒也会导致程序的性能受到影响,因为唤醒的线程会引入额外的开销,浪费了CPU资源。
虚假唤醒的几种场景:
条件变量虚假唤醒指的是在多线程编程中,使用条件变量进行同步时,某个线程在未满足条件的情况下被唤醒的情况。
有几种场景可能导致条件变量虚假唤醒,比如:
- 多个线程在等待同一个条件变量时,其中一个线程被误唤醒,导致其他线程也被唤醒。
- 条件变量在等待之前没有正确的设置条件,导致其他线程没有满足条件就被唤醒。
- 在条件变量的 wait 函数返回之前,其他线程已经修改了满足条件的变量,导致当前线程在检查条件时发现条件已经被满足了。
- 唤醒信号丢失:当一个线程在等待条件变量时,另一个线程发出唤醒信号,但该信号可能会被操作系统丢失。
- 操作系统信号处理:当线程被操作系统中断处理程序唤醒时,可能会发生虚假唤醒。
以上这些情况都可能导致条件变量的虚假唤醒。
解决办法:
为了避免条件变量虚假唤醒,可以使用while循环重新检查等待条件。当线程在等待条件变量时,需要通过while循环来重新检查是否达到等待条件,条件不满足则再次wait。这样可以防止线程在没有满足条件的情况下被误唤醒。
例如,在等待条件变量的代码中,可以使用如下方式来避免虚假唤醒:
unique_lock<mutex> lock(mtx);
while(!condition){
cond_var.wait(lock); }上述代码将条件判断和等待的操作放在一个while循环中,当线程被唤醒后,再次检查条件是否满足,如果不满足,则继续等待。
需要注意的是,虽然使用while循环可以避免虚假唤醒,但也会导致程序性能下降,因为线程需要不断地检查条件。此外,while循环也可能会导致死锁,需要仔细设计条件变量的使用方式。
总之,为了避免条件变量的虚假唤醒,应该使用while循环重新检查等待条件,但也需要注意该方式可能会影响程序性能和出现死锁等问题。
其他:
- 当消费者的数量(CONSUMER_NUM)为1时没有其他线程竞争队列,不会触发虚假唤醒。
- 当生产者的数量(PRODUCTER_NUM)为1时,
- 当使用notify_one通知消费线程时,不会发生虚假唤醒,因为每次只会有一个消费者线程收到信号被唤醒,在产品被消耗掉之前不会有新的信号发出来。
- 当使用notify_all通知消费线程时,会发生虚假唤醒,会有多个消费者线程收到信号被唤醒,当一个线程被唤醒之前,可能其他线程先被唤醒先持有锁,将产品消耗掉。
- 当生产者的数量(PRODUCTER_NUM)大于1时,无论是使用notify_one,或者是notify_all都会发生虚假唤醒,当多个生产者使用notify_one时,多个线程被唤醒,有可能其中一个处理的特别快,将所有的数据都处理完毕,那么接下来被唤醒的线程都无数据可处理。
相关文章:

C++虚假唤醒
概念: 虚假唤醒是指在使用条件变量时,线程被唤醒但条件并没有满足,导致线程执行错误的情况,这个过程就是虚假唤醒。 虚假唤醒弊端: 虚假唤醒会导致程序的正确性受到影响,因为唤醒的线程并没有满足条件&…...

【AI】dragonGPT - 单机部署、极速便捷
dragonGPT 从数据私有化,到prompt向量库匹配,再到查询,一条龙服务,单机部署,极简操作 pre a.需要下载gpt4all model到本地. ggml Model Download Link 然后将存放model的地址写入.env MODEL_PATH your pathb.…...

Uuiapp使用生命周期,路由跳转传参
Uniapp生命周期: 1. beforeCreate:在实例初始化之后,数据观测和事件配置之前被调用。 2. created:在实例创建完成后被立即调用。 3. beforeMount:在挂载开始之前被调用:相关的 render 函数首次被调用。 …...
习题)
定积分的计算(牛顿-莱布尼茨公式)习题
前置知识:定积分的计算(牛顿-莱布尼茨公式) 习题1 计算 ∫ 0 2 ( x 2 − 2 x 3 ) d x \int_0^2(x^2-2x3)dx ∫02(x2−2x3)dx 解: \qquad 原式 ( 1 3 x 3 − x 2 3 x ) ∣ 0 2 ( 8 3 − 4 6 ) − 0 14 3 (\dfrac 13x^3-…...

leak 记录今天的一个小题
先看题, add没有大小限制,这里edit可以溢出8字节,也就是可以改后边的size,可以调用4次free没有调用函数只是把指针置0,show可以用一次. void __fastcall __noreturn main(__int64 a1, char **a2, char **a3) {init_0(a1, a2, a3);while ( 1 ){menu();switch ( read_n() ){cas…...

软考A计划-试题模拟含答案解析-卷二
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...

【C++】pthread
一、pthread简介 pthread是C98接口且只支持Linux,使用时需要包含头文件#include <pthread.h>,编译时需要链接pthread库,其中p是POSIX的缩写,而POSIX是Portable Operating System Interface的缩写,是IEEE为要在各…...
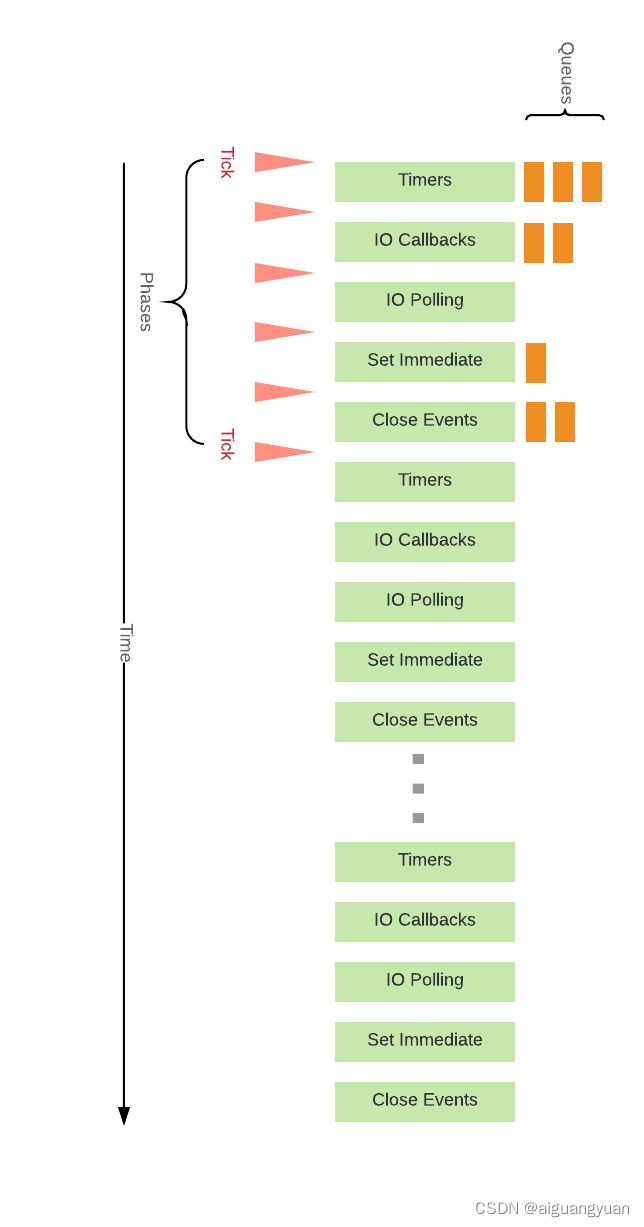
2023年前端面试题汇总-浏览器原理
1. 浏览器安全 1.1. 什么是 XSS 攻击? 1.1. 1. 概念 XSS 攻击指的是跨站脚本攻击,是一种代码注入攻击。攻击者通过在网站注入恶意脚本,使之在用户的浏览器上运行,从而盗取用户的信息如 cookie 等。 XSS 的本质是因为网站没有对…...

react介绍,react语法,react高级特性,react编程技巧
React是一个用于构建用户界面的JavaScript库。它由Facebook开发,于2013年首次发布。React的主要目标是提高应用程序的性能和可维护性。React采用了一种称为“组件”的模式,使开发人员可以将应用程序拆分为小而独立的部分,从而更容易编写和维护…...
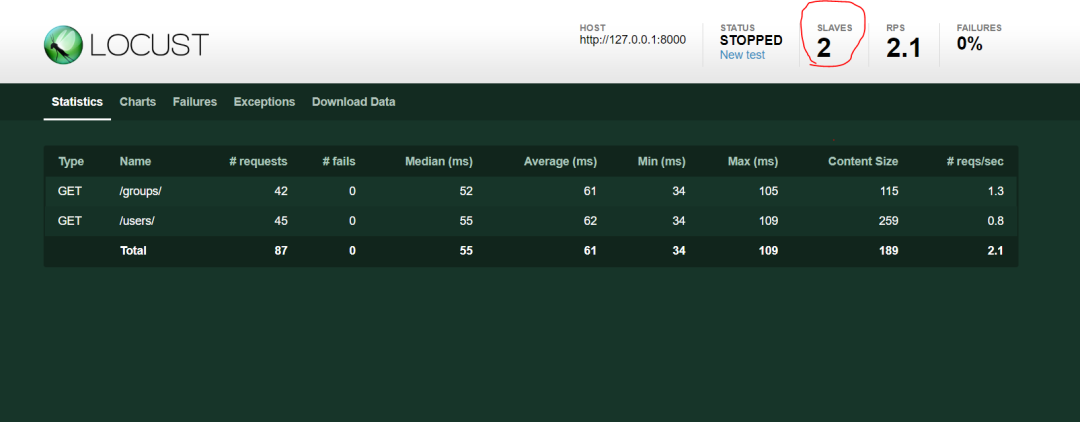
Locust接口性能测试
谈到性能测试工具,我们首先想到的是LoadRunner或JMeter。LoadRunner是非常有名的商业性能测试工具,功能非常强大。但现在一般不推荐使用该工具来进行性能测试,主要是使用也较为复杂,而且该工具体积比较大,需要付费且价…...
)
Python类的特殊方法(通过故事来学习)
在一座森林里,住着三只动物:狼、兔和熊。这三只动物都有不同的特点和能力,但是它们所有的行为都可以被抽象成一个“动物”类。现在,让我们来看看Python中的类和特殊方法如何帮助我们实现这个故事。 首先,我们可以定义…...

Vue.js 中的父子组件通信方式
Vue.js 中的父子组件通信方式 在 Vue.js 中,组件是构建应用程序的基本单元。当我们在应用程序中使用组件时,组件之间的通信是非常重要的。在 Vue.js 中,父子组件通信是最常见的组件通信方式之一。在本文中,我们将讨论 Vue.js 中的…...
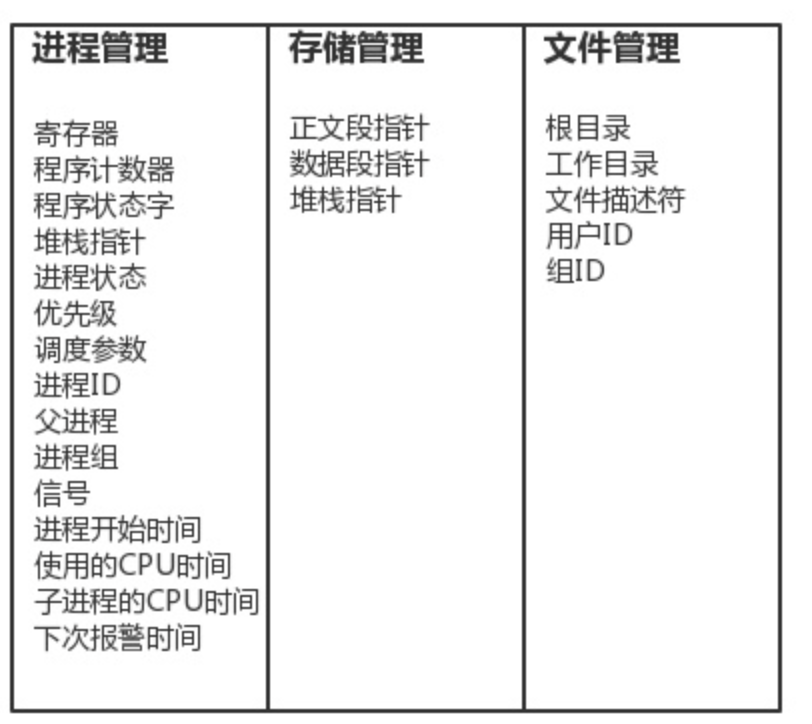
Python之并发编程二多进程理论
一、什么是进程 进程:正在进行的一个过程或者说一个任务。而负责执行任务则是cpu。 二、进程与程序的区别 程序仅仅只是一堆代码而已,而进程指的是程序的运行过程。 三、并发与并行 无论是并行还是并发,在用户看来都是’同时’运行的&am…...
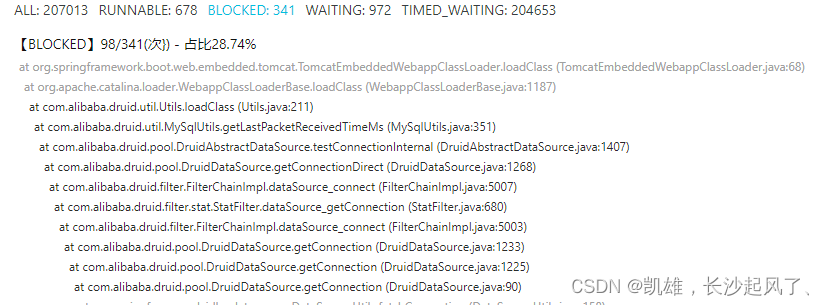
纯干货:数据库连接耗时慢原因排查
背景 最近公司的社区相关的服务需要优化,由于对业务不熟悉,只能借助监控从一些慢接口开始尝试探索慢的原因。由于社区相关的功能务是公司小程序流量入口,所以相应的服务访问量还是比较高的。针对这类高访问的项目,任何不留神的地…...
【OneNet】| stm32+esp8266-01s—— OneNet初体验 | 平台注册及设备创建 | demo使用
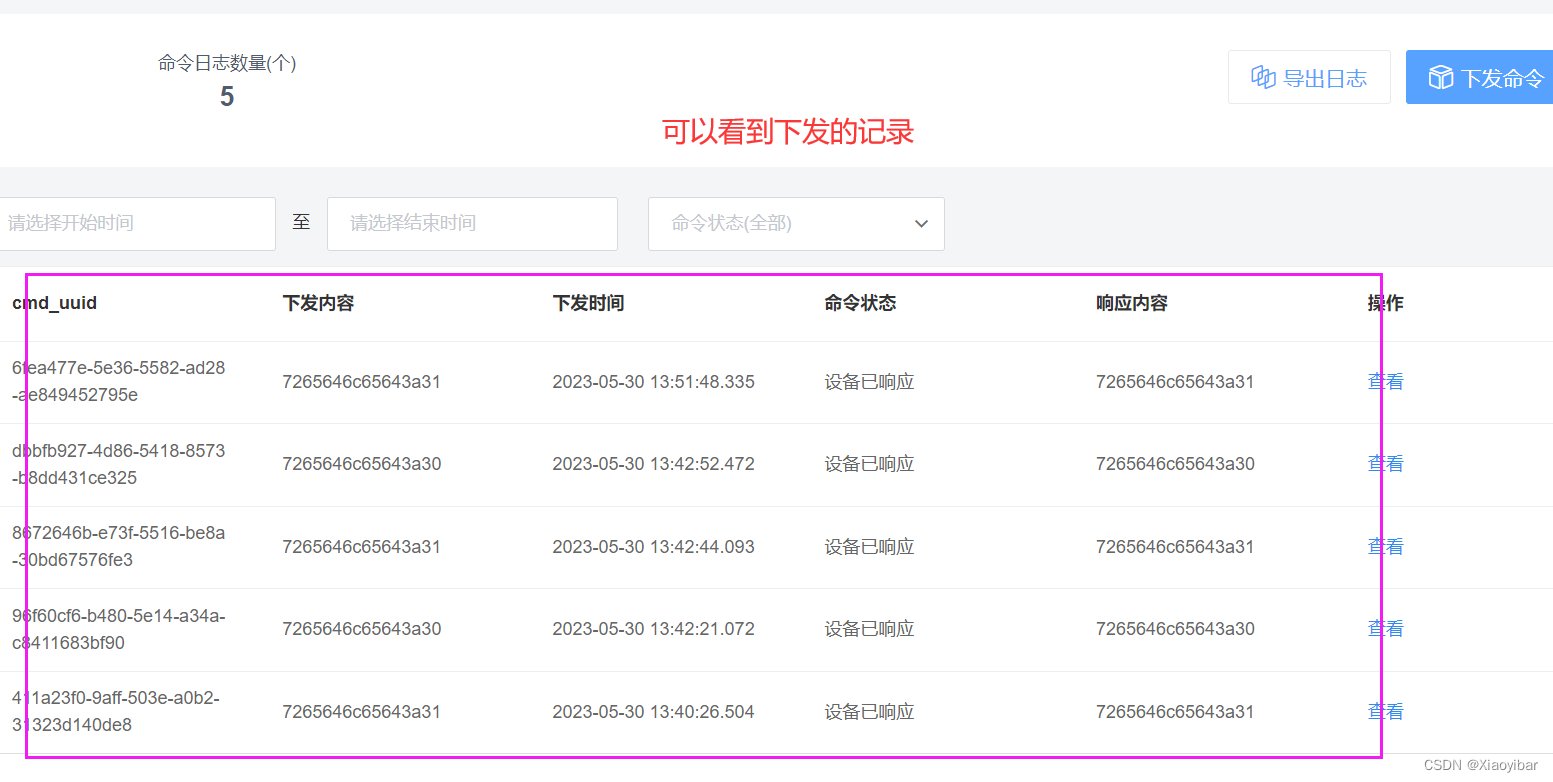
系列文章目录 失败了也挺可爱,成功了就超帅。 文章目录 前言1. OneNet平台注册2. 创建多协议接入设备3. 硬件连接4. 下载并运行Demo4.1 Demo下载4.2 运行Demo本小节结束 前言 最近准备耍下 Onenet平台 。下载了官方demo 遇到几个问题 1、创建接入设备 因为平台网页…...
解决win无法删除多层嵌套文件夹
起因:昨天研究jpackage工具,不小心搞得一个文件夹里嵌套了好几百个文件夹,用win自己的删除删不掉,shiftdel直接删除也不行,直接弹窗删除错误; 后来用电脑管家下载了个“文件粉碎”,添加目录&am…...

用Vue简单开发一个学习界面
文章目录 一.首先创建我们的Vue文件夹二.源代码BodyDemoHearderDemoHomeDemoMarkdownDemoFileManager.jsMain.js(注意绑定)APP源代码 效果图(按钮功能)新增二级菜单(v-for)需要的可以私信 一.首先创建我们的…...

Oracle数据库从入门到精通系列之五:数据文件
Oracle数据库从入门到精通系列之五:数据文件 一、数据文件二、Oracle数据库存储分配单位三、Oracle数据库文件系统机制四、段五、区段六、块七、表空间八、Oracle数据库存储层次体系小结一、数据文件 数据文件和重做文件是数据库中最重要的文件,数据最终会存储在这些文件中。…...
使用MockJS进行前端开发中的数据模拟
在前端开发中,有时我们需要在没有后端接口的情况下进行前端页面的开发和测试。这时,我们可以使用MockJS来模拟数据,以便进行开发和调试。MockJS是一个用于生成随机数据和拦截Ajax请求的JavaScript库,它能够帮助我们快速搭建起一个…...
Ex-ChatGPT本地部署+Azure OpenAI接口配置+docker部署服务
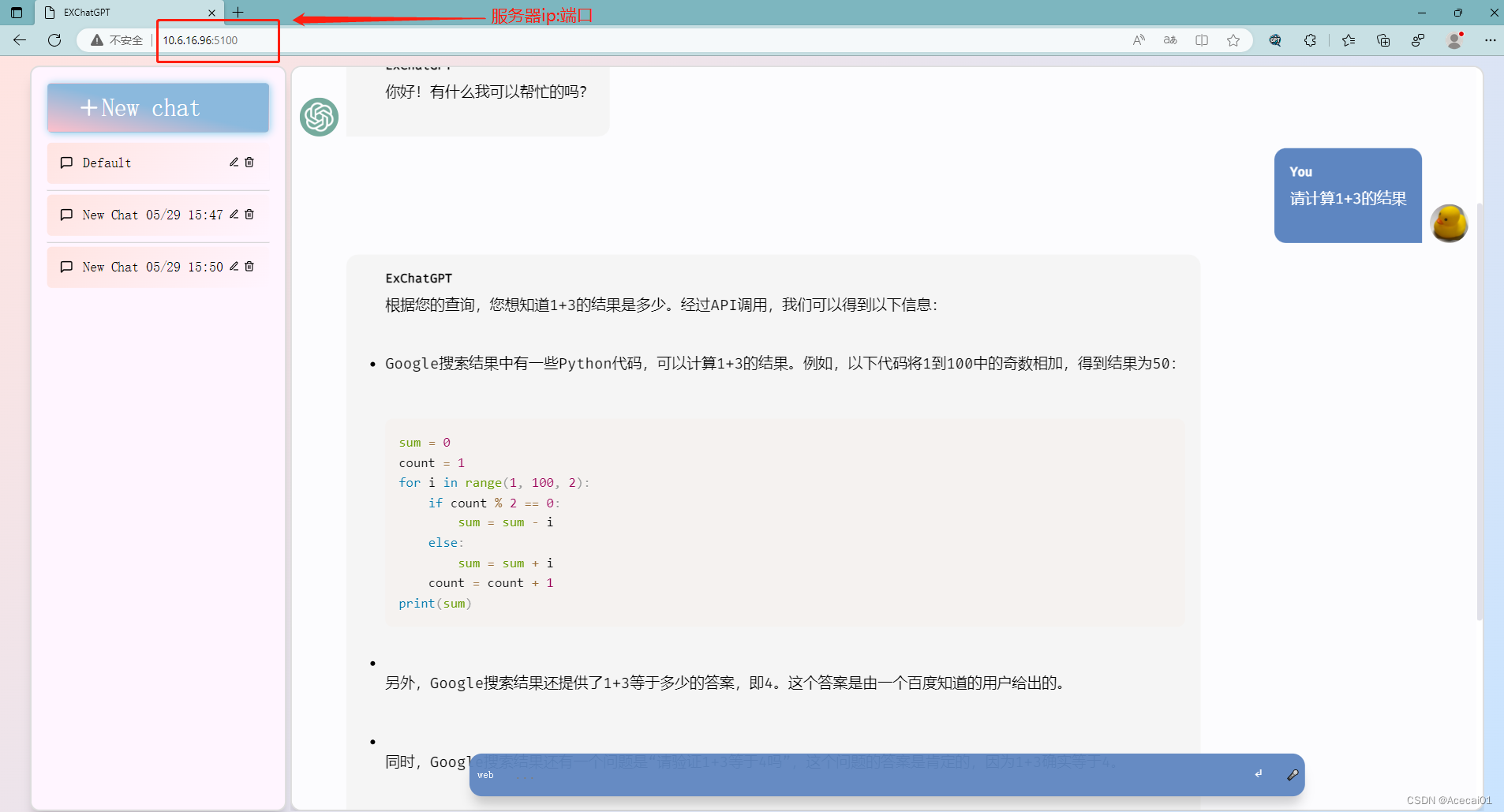
Ex-ChatGPT项目分为 Ex-ChatGPT 和 WebChatGPTEnhance 两部分,Ex-ChatGPT启动后是个web服务,通过访问ip端口体验; WebChatGPTEnhance可编译生成一个浏览器插件,Chrome或者Microsoft edge浏览器可以安装该插件,点击该插…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
