【小呆的力学笔记】非线性有限元的初步认识【三】
文章目录
- 1.2.2 基于最小势能原理的线性有限元一般格式
- 1.2.2.1 离散化
- 1.2.2.2 位移插值
- 1.2.2.3 单元应变
- 1.2.2.4 单元应力
- 1.2.2.5 单元刚度矩阵
- 1.2.2.6 整体刚度矩阵
- 1.2.2.7 处理约束
- 1.2.2.8 求解节点载荷列阵
- 1.2.2.9 求解位移列阵
- 1.2.2.10 计算应力矩阵等
1.2.2 基于最小势能原理的线性有限元一般格式
现在市场上的有限元分析软件普遍都是基于位移法进行求解的,其数学原理就是上节的最小势能原理变分提法。回顾上节推导过程,首先需要根据位移条件确定可能位移的范围,其次根据假设的可能位移代入几何方程和本构方程,得到基于位移的应力应变的表达式,最后代入 δ I I = 0 \delta II=0 δII=0的方程求解相关待定参数。线性有限元求解的一般格式基本上也是一样的,除此之外线性有限元会多一些其他步骤,比如结构的离散化、位移模式假定等。下图为线性有限元求解的一般格式。
(加图)
1.2.2.1 离散化
将结构进行离散化建模,是有限元分析工作中的第一步,某典型的结构如下图所示,其中结构为一个圆盘,将其离散成若干四边形网格单元,如下图所示。结构离散化合适与否一定程度上决定使用有限元分析方法解决工程问题的精度。
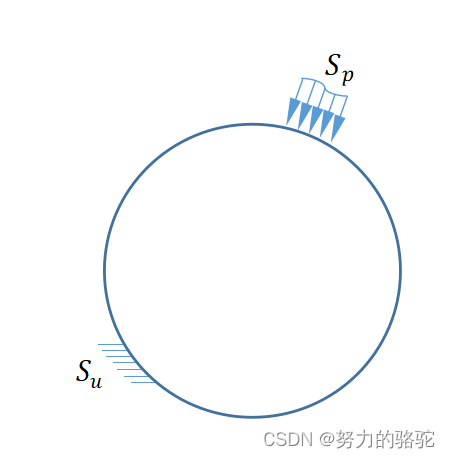

1.2.2.2 位移插值
(a)位移模式
在最小势能原理中首先需要根据位移条件确定可能位移的范围,但是在通常的分析中,我们为了方便处理,往往将可能位移用多项式来逼近,这个过程就是单元的位移模式选择。
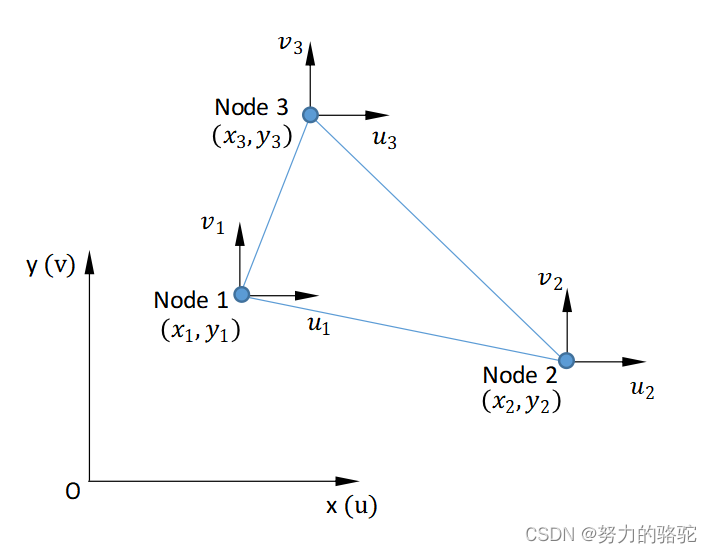
我们以一阶二维三角形单元为例,二维三角形单元有6各位移自由度。用多项式拟合可能位移,如下式所示
u ( x , y ) = a ‾ 0 + a ‾ 1 x + a ‾ 2 y v ( x , y ) = b ‾ 0 + b ‾ 1 x + b ‾ 2 y (1-54) \begin{aligned} u(x,y)=\overline a_{0}+\overline a_{1}x+\overline a_{2}y\\ v(x,y)=\overline b_{0}+\overline b_{1}x+\overline b_{2}y \end{aligned}\tag{1-54} u(x,y)=a0+a1x+a2yv(x,y)=b0+b1x+b2y(1-54)
(b)形函数
多项式位移模式有六个待定参数,二维三角形单元有六个节点位移变量,所以六个待定参数可以表示成六个节点位移变量的形式,如下式,待定系数满足下式。
[ u 1 u 2 u 3 ] = [ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] [ a ‾ 0 a ‾ 1 a ‾ 2 ] , [ v 1 v 2 v 3 ] = [ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] [ b ‾ 0 b ‾ 1 b ‾ 2 ] (1-55) \begin{aligned} \begin{bmatrix} u_1\\ u_2\\ u_3\\ \end{bmatrix}= \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix} \begin{bmatrix} \overline a_0\\ \overline a_1\\ \overline a_2\\ \end{bmatrix}, \begin{bmatrix} v_1\\ v_2\\ v_3\\ \end{bmatrix}= \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix} \begin{bmatrix} \overline b_0\\ \overline b_1\\ \overline b_2\\ \end{bmatrix} \end{aligned}\tag{1-55} u1u2u3 = 111x1x2x3y1y2y3 a0a1a2 , v1v2v3 = 111x1x2x3y1y2y3 b0b1b2 (1-55)
那么系数为
[ a ‾ 0 a ‾ 1 a ‾ 2 ] = [ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] − 1 [ u 1 u 2 u 3 ] , [ b ‾ 0 b ‾ 1 b ‾ 2 ] = [ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] − 1 [ v 1 v 2 v 3 ] (1-56) \begin{aligned} \begin{bmatrix} \overline a_0\\ \overline a_1\\ \overline a_2\\ \end{bmatrix}= \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix}^{-1} \begin{bmatrix} u_1\\u_2\\u_3\\ \end{bmatrix}, \begin{bmatrix} \overline b_0\\ \overline b_1\\ \overline b_2\\ \end{bmatrix}= \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix}^{-1} \begin{bmatrix} v_1\\ v_2\\ v_3\\ \end{bmatrix} \end{aligned}\tag{1-56} a0a1a2 = 111x1x2x3y1y2y3 −1 u1u2u3 , b0b1b2 = 111x1x2x3y1y2y3 −1 v1v2v3 (1-56)
其中逆矩阵的求解如下
[ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] − 1 = [ M i j ⋅ ( − 1 ) i + j ] T A (1-57) \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix}^{-1}=\frac{[M_{ij}\cdot (-1)^{i+j}]^T}{A}\tag{1-57} 111x1x2x3y1y2y3 −1=A[Mij⋅(−1)i+j]T(1-57)
其中 M i j M_{ij} Mij为原矩阵的余子式,典型如下,其乘上 ( − 1 ) i + j (-1)^{i+j} (−1)i+j称为代数余子式,矩阵的逆是其代数余子式组成的伴随矩阵除以该矩阵的行列式。

经过求解,系数矩阵的逆矩阵如下式
[ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ] − 1 = ∣ 1 x 1 y 1 1 x 2 y 2 1 x 3 y 3 ∣ − 1 ⋅ [ ∣ x 2 y 2 x 3 y 3 ∣ − ∣ x 1 y 1 x 3 y 3 ∣ ∣ x 1 y 1 x 2 y 2 ∣ − ∣ 1 y 2 1 y 3 ∣ ∣ 1 y 1 1 y 3 ∣ − ∣ 1 y 1 1 y 2 ∣ ∣ 1 x 2 1 x 3 ∣ − ∣ 1 x 1 1 x 3 ∣ ∣ 1 x 1 1 x 2 ∣ ] = 1 A [ a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ] (1-58) \begin{aligned} \begin{bmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{bmatrix}^{-1}&= \begin{vmatrix} 1 & x_1 & y_1\\ 1 & x_2 & y_2\\ 1 & x_3 & y_3\\ \end{vmatrix}^{-1}\cdot \begin{bmatrix} \begin{vmatrix} x_2 & y_2\\ x_3 & y_3\\ \end{vmatrix} & -\begin{vmatrix} x_1 & y_1\\ x_3 & y_3\\ \end{vmatrix} & \begin{vmatrix} x_1 & y_1\\ x_2 & y_2\\ \end{vmatrix}\\ & & \\ -\begin{vmatrix} 1 & y_2\\ 1 & y_3\\ \end{vmatrix} & \begin{vmatrix} 1 & y_1\\ 1 & y_3\\ \end{vmatrix} & -\begin{vmatrix} 1 & y_1\\ 1 & y_2\\ \end{vmatrix}\\& & \\ \begin{vmatrix} 1 & x_2\\ 1 & x_3\\ \end{vmatrix} & -\begin{vmatrix} 1 & x_1\\ 1 & x_3\\ \end{vmatrix} & \begin{vmatrix} 1 & x_1\\ 1 & x_2\\ \end{vmatrix}\\ \end{bmatrix} \\=\frac{1}{A}\begin{bmatrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3\\ \end{bmatrix} \end{aligned}\tag{1-58} 111x1x2x3y1y2y3 −1=A1 a1b1c1a2b2c2a3b3c3 = 111x1x2x3y1y2y3 −1⋅ x2x3y2y3 − 11y2y3 11x2x3 − x1x3y1y3 11y1y3 − 11x1x3 x1x2y1y2 − 11y1y2 11x1x2 (1-58)
那么,系数可以表达成
a ‾ 0 = 1 A ( a 1 u 1 + a 2 u 2 + a 3 u 3 ) a ‾ 1 = 1 A ( b 1 u 1 + b 2 u 2 + b 3 u 3 ) a ‾ 2 = 1 A ( c 1 u 1 + c 2 u 2 + c 3 u 3 ) (1-59) \begin{aligned} \overline a_0=\frac{1}{A}(a_1u_1+a_2u_2+a_3u_3)\\ \overline a_1=\frac{1}{A}(b_1u_1+b_2u_2+b_3u_3)\\ \overline a_2=\frac{1}{A}(c_1u_1+c_2u_2+c_3u_3) \end{aligned}\tag{1-59} a0=A1(a1u1+a2u2+a3u3)a1=A1(b1u1+b2u2+b3u3)a2=A1(c1u1+c2u2+c3u3)(1-59)
上式代入位移模式,可得
u ( x , y ) = a ‾ 0 + a ‾ 1 x + a ‾ 2 y = 1 A ( a 1 u 1 + a 2 u 2 + a 3 u 3 ) + 1 A ( b 1 u 1 + b 2 u 2 + b 3 u 3 ) x + 1 A ( c 1 u 1 + c 2 u 2 + c 3 u 3 ) y = 1 A ( a 1 + b 1 x + c 1 y ) u 1 + 1 A ( a 2 + b 2 x + c 2 y ) u 2 + 1 A ( a 3 + b 3 x + c 3 y ) u 3 = N 1 ( x , y ) u 1 + N 2 ( x , y ) u 2 + N 3 ( x , y ) u 3 (1-60) \begin{aligned} u(x,y)&=\overline a_{0}+\overline a_{1}x+\overline a_{2}y\\ &=\frac{1}{A}(a_1u_1+a_2u_2+a_3u_3)+\frac{1}{A}(b_1u_1+b_2u_2+b_3u_3)x+\frac{1}{A}(c_1u_1+c_2u_2+c_3u_3)y\\ &=\frac{1}{A}(a_1+b_1x+c_1y)u_1+\frac{1}{A}(a_2+b_2x+c_2y)u_2+\frac{1}{A}(a_3+b_3x+c_3y)u_3\\ &=N_1(x,y)u_1+N_2(x,y)u_2+N_3(x,y)u_3 \end{aligned}\tag{1-60} u(x,y)=a0+a1x+a2y=A1(a1u1+a2u2+a3u3)+A1(b1u1+b2u2+b3u3)x+A1(c1u1+c2u2+c3u3)y=A1(a1+b1x+c1y)u1+A1(a2+b2x+c2y)u2+A1(a3+b3x+c3y)u3=N1(x,y)u1+N2(x,y)u2+N3(x,y)u3(1-60)
同理,可得
v ( x , y ) = a ‾ 0 + a ‾ 1 x + a ‾ 2 y = 1 A ( a 1 v 1 + a 2 v 2 + a 3 v 3 ) + 1 A ( b 1 v 1 + b 2 v 2 + b 3 v 3 ) x + 1 A ( c 1 v 1 + c 2 v 2 + c 3 v 3 ) y = 1 A ( a 1 + b 1 x + c 1 y ) v 1 + 1 A ( a 2 + b 2 x + c 2 y ) v 2 + 1 A ( a 3 + b 3 x + c 3 y ) v 3 = N 1 ( x , y ) v 1 + N 2 ( x , y ) v 2 + N 3 ( x , y ) v 3 (1-61) \begin{aligned} v(x,y)&=\overline a_{0}+\overline a_{1}x+\overline a_{2}y\\ &=\frac{1}{A}(a_1v_1+a_2v_2+a_3v_3)+\frac{1}{A}(b_1v_1+b_2v_2+b_3v_3)x+\frac{1}{A}(c_1v_1+c_2v_2+c_3v_3)y\\ &=\frac{1}{A}(a_1+b_1x+c_1y)v_1+\frac{1}{A}(a_2+b_2x+c_2y)v_2+\frac{1}{A}(a_3+b_3x+c_3y)v_3\\ &=N_1(x,y)v_1+N_2(x,y)v_2+N_3(x,y)v_3 \end{aligned}\tag{1-61} v(x,y)=a0+a1x+a2y=A1(a1v1+a2v2+a3v3)+A1(b1v1+b2v2+b3v3)x+A1(c1v1+c2v2+c3v3)y=A1(a1+b1x+c1y)v1+A1(a2+b2x+c2y)v2+A1(a3+b3x+c3y)v3=N1(x,y)v1+N2(x,y)v2+N3(x,y)v3(1-61)
可以将二维三角形单元内任意一点的位移写成矩阵的形式,如下
u ( x , y ) = [ u ( x , y ) v ( x , y ) ] = [ N 1 ( x , y ) 0 N 2 ( x , y ) 0 N 3 ( x , y ) 0 0 N 1 ( x , y ) 0 N 2 ( x , y ) 0 N 3 ( x , y ) ] [ u 1 v 1 u 2 v 2 u 3 v 3 ] = N ( x , y ) ⋅ q e (1-62) \begin{aligned} \mathbf u(x,y) = \begin{bmatrix} u(x,y)\\ v(x,y)\\ \end{bmatrix}&= \begin{bmatrix} N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y) & 0\\ 0 & N_1(x,y) & 0 & N_2(x,y) & 0 & N_3(x,y)\\ \end{bmatrix} \begin{bmatrix} u_1\\v_1\\u_2\\v_2\\u_3\\v_3 \end{bmatrix}\\&=\mathbf N(x,y)\cdot \mathbf q^e \end{aligned}\tag{1-62} u(x,y)=[u(x,y)v(x,y)]=[N1(x,y)00N1(x,y)N2(x,y)00N2(x,y)N3(x,y)00N3(x,y)] u1v1u2v2u3v3 =N(x,y)⋅qe(1-62)
我们称 N ( x , y ) \mathbf N(x,y) N(x,y)为形状函数矩阵,而 q e \mathbf q^e qe为单元的节点位移列阵。形状函数矩阵作用 就是用节点位移列阵插值得到任意一点位移的插值函数。
1.2.2.3 单元应变
应变和位移的关系由几何方程确定,在本文二维的例子中,应变仅有三个分量,那么应变与位移的关系可以如下式所示。
ε ( x , y ) = [ ε x x ε y y γ x y ] = [ ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y + ∂ v ∂ x ] = [ ∂ ∂ x 0 0 ∂ ∂ y ∂ ∂ y ∂ ∂ x ] ⋅ [ u ( x , y ) v ( x , y ) ] = [ ∂ ∂ x 0 0 ∂ ∂ y ∂ ∂ y ∂ ∂ x ] ⋅ N ( x , y ) ⋅ q e = B ( x , y ) ⋅ q e (1-63) \begin{aligned} \boldsymbol{\varepsilon}(x,y) = \begin{bmatrix} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \gamma_{xy} \end{bmatrix}= \begin{bmatrix} \frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} \end{bmatrix}&= \begin{bmatrix} \frac{\partial }{\partial x} & 0\\ 0 & \frac{\partial }{\partial y}\\ \frac{\partial }{\partial y} & \frac{\partial }{\partial x} \end{bmatrix}\cdot \begin{bmatrix} u(x,y)\\ v(x,y) \end{bmatrix}\\&=\begin{bmatrix} \frac{\partial }{\partial x} & 0\\ 0 & \frac{\partial }{\partial y}\\ \frac{\partial }{\partial y} & \frac{\partial }{\partial x} \end{bmatrix}\cdot\mathbf N(x,y)\cdot \mathbf q^e\\&=\mathbf B(x,y)\cdot \mathbf q^e \end{aligned}\tag{1-63} ε(x,y)= εxxεyyγxy = ∂x∂u∂y∂v∂y∂u+∂x∂v = ∂x∂0∂y∂0∂y∂∂x∂ ⋅[u(x,y)v(x,y)]= ∂x∂0∂y∂0∂y∂∂x∂ ⋅N(x,y)⋅qe=B(x,y)⋅qe(1-63)
1.2.2.4 单元应力
应力应变关系又成本构方程,在线性范围内,应力与应变的关系写成矩阵如下(本例中为二维三角形单元,应力分量只有三个)
σ ( x , y ) = [ σ x x σ y y τ x y ] = E 1 − μ 2 [ 1 μ 0 μ 1 0 0 0 1 − μ 2 ] [ ε x x ε y y γ x y ] = D ( x , y ) ⋅ ε ( x , y ) = D ( x , y ) ⋅ B ( x , y ) ⋅ q e = S ( x , y ) ⋅ q e (1-64) \begin{aligned} \boldsymbol{\sigma}(x,y) = \begin{bmatrix} \sigma_{xx}\\ \sigma_{yy}\\ \tau_{xy} \end{bmatrix}&= \frac{E}{1-\mu^2}\begin{bmatrix} 1 & \mu & 0\\ \mu & 1 & 0\\ 0 & 0 & \frac{1-\mu}{2} \end{bmatrix}\begin{bmatrix} \varepsilon_{xx}\\ \varepsilon_{yy}\\ \gamma_{xy} \end{bmatrix}\\ &=\mathbf D(x,y)\cdot \boldsymbol{\varepsilon}(x,y)\\ &=\mathbf D(x,y)\cdot \mathbf B(x,y)\cdot \mathbf q^e\\ &=\mathbf S(x,y)\cdot \mathbf q^e \end{aligned}\tag{1-64} σ(x,y)= σxxσyyτxy =1−μ2E 1μ0μ100021−μ εxxεyyγxy =D(x,y)⋅ε(x,y)=D(x,y)⋅B(x,y)⋅qe=S(x,y)⋅qe(1-64)
1.2.2.5 单元刚度矩阵
回顾物体的总势能表达式,并将其写成矩阵的形式
I I = 1 2 ∫ Ω σ i j ε i j d Ω − ∫ Ω b i u i d Ω − ∫ A p i u i d A = 1 2 ∫ Ω σ T ε d Ω − ∫ Ω b T u d Ω − ∫ A p T u d A (1-65) \begin{aligned} II&=\frac{1}{2}\int_{\Omega}\sigma_{ij}\varepsilon_{ij}d\Omega-\int_{\Omega} b_{i}u_{i}d\Omega -\int_{A}p_{i}u_{i}dA\\ &=\frac{1}{2}\int_{\Omega}\boldsymbol{\sigma}^T\boldsymbol{\varepsilon}\mathbf d\Omega-\int_{\Omega} \mathbf b^T \mathbf u \mathbf d\Omega -\int_{A}\mathbf p^T\mathbf u \mathbf dA \end{aligned}\tag{1-65} II=21∫ΩσijεijdΩ−∫ΩbiuidΩ−∫ApiuidA=21∫ΩσTεdΩ−∫ΩbTudΩ−∫ApTudA(1-65)
将前述单元的应力、应变矩阵等代入上式,建立单元的总势能表达式,如下所示
I I = 1 2 ∫ Ω σ T ε d Ω − ∫ Ω b T u d Ω − ∫ A p T u d A = 1 2 ∫ Ω q e T B T D T B q e d Ω − ∫ Ω b T N q e d Ω − ∫ A p T N q e d A = 1 2 q e T ( ∫ Ω B T D T B d Ω ) q e − ( ∫ Ω b T N d Ω + ∫ A p T N d A ) q e = 1 2 q e T K e q e − P e T q e (1-66) \begin{aligned} II &=\frac{1}{2}\int_{\Omega}\boldsymbol{\sigma}^T\boldsymbol{\varepsilon}\mathbf d\Omega-\int_{\Omega} \mathbf b^T \mathbf u \mathbf d\Omega -\int_{A}\mathbf p^T\mathbf u \mathbf dA\\ &=\frac{1}{2}\int_{\Omega}\boldsymbol{q^e}^T\boldsymbol{B^TD^TBq^e}\mathbf d\Omega-\int_{\Omega} \mathbf b^T \boldsymbol{ Nq^e d}\Omega -\int_{A}\mathbf p^T\boldsymbol{ Nq^e d}A\\ &=\frac{1}{2}\boldsymbol{q^e}^T(\int_{\Omega}\boldsymbol{B^TD^TB d}\Omega)\boldsymbol{q^e}-(\int_{\Omega} \mathbf b^T \boldsymbol{ Nd}\Omega +\int_{A}\mathbf p^T\boldsymbol{ Nd}A)\boldsymbol{q^e}\\ &=\frac{1}{2}\boldsymbol{q^e}^T\boldsymbol{K^e}\boldsymbol{q^e}-\boldsymbol{P^e}^T\boldsymbol{q^e} \end{aligned}\tag{1-66} II=21∫ΩσTεdΩ−∫ΩbTudΩ−∫ApTudA=21∫ΩqeTBTDTBqedΩ−∫ΩbTNqedΩ−∫ApTNqedA=21qeT(∫ΩBTDTBdΩ)qe−(∫ΩbTNdΩ+∫ApTNdA)qe=21qeTKeqe−PeTqe(1-66)
回顾之前最小势能原理,真实位移是使得势能取得最小值,上式是单元的总势能,那么真实的位移使得势能取到最小值,也就是说总势能一阶变分为零,即
δ I I = ∂ I I ∂ q e δ q e = ( K e q e − P e ) δ q e = 0 (1-67) \delta II = \frac{\partial II}{\partial q^e}\delta q^e=(\boldsymbol{K^e}\boldsymbol{q^e}-\boldsymbol{P^e})\delta q^e=0 \tag{1-67} δII=∂qe∂IIδqe=(Keqe−Pe)δqe=0(1-67)
由于 δ q e \delta q^e δqe的任意性,可以得到
K e q e − P e = 0 (1-68) \boldsymbol{K^e}\boldsymbol{q^e}-\boldsymbol{P^e}=0\tag{1-68} Keqe−Pe=0(1-68)
其中 K e \boldsymbol{K^e} Ke为单元刚度矩阵(由上式中的量纲分析, K e \boldsymbol{K^e} Ke为刚度的量纲), P e \boldsymbol{P^e} Pe为节点等效载荷。
1.2.2.6 整体刚度矩阵
对于物体来说,一般有多个单元,那么就可以建立多个单元平衡方程,如下所示
K ( i ) e q ( i ) e − P ( i ) e = 0 (1-69) \boldsymbol{K^e_{(i)}}\boldsymbol{q^e_{(i)}}-\boldsymbol{P^e_{(i)}}=0\tag{1-69} K(i)eq(i)e−P(i)e=0(1-69)
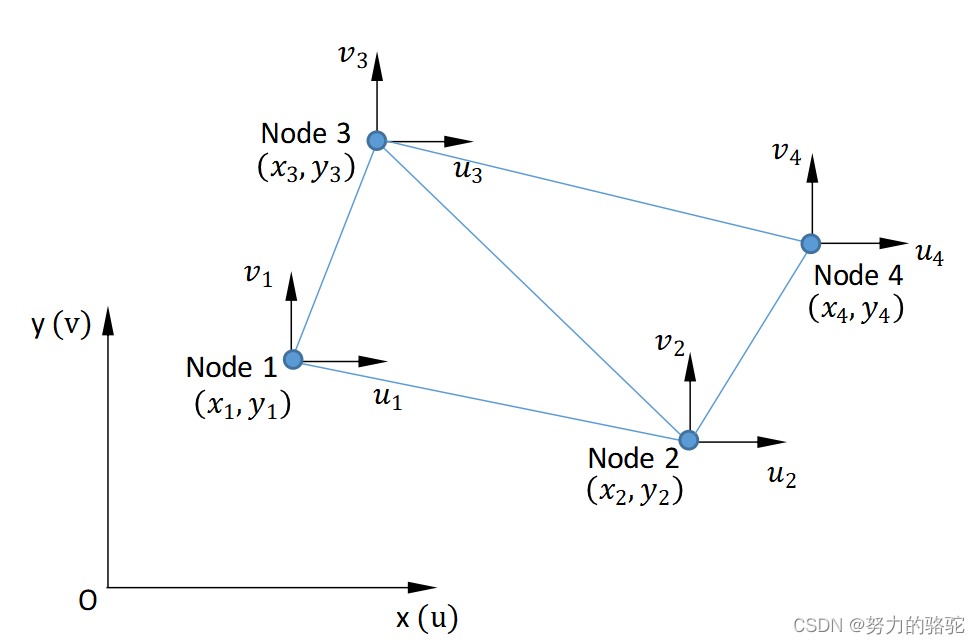
按照顺序将所有的单元的节点位移组成总体节点位移列阵,相应的节点等效载荷和单元刚度矩阵组成总体节点等效载荷列阵和整体刚度矩阵,以下图为例,下图总共有两个单元,得到两个单元平衡方程
[ k 11 1 k 12 1 k 13 1 k 14 1 k 15 1 k 16 1 k 21 1 k 22 1 k 23 1 k 24 1 k 25 1 k 26 1 k 31 1 k 32 1 k 33 1 k 34 1 k 35 1 k 36 1 k 41 1 k 42 1 k 43 1 k 44 1 k 45 1 k 46 1 k 51 1 k 52 1 k 53 1 k 54 1 k 55 1 k 56 1 k 61 1 k 62 1 k 63 1 k 64 1 k 65 1 k 66 1 ] [ u 1 v 1 u 2 v 2 u 3 v 3 ] = [ p x 1 1 p y 1 1 p x 2 1 p y 2 1 p x 3 1 p y 3 1 ] [ k 11 2 k 12 2 k 13 2 k 14 2 k 15 2 k 16 2 k 21 2 k 22 2 k 23 2 k 24 2 k 25 2 k 26 2 k 31 2 k 32 2 k 33 2 k 34 2 k 35 2 k 36 2 k 41 2 k 42 2 k 43 2 k 44 2 k 45 2 k 46 2 k 51 2 k 52 2 k 53 2 k 54 2 k 55 2 k 56 2 k 61 2 k 62 2 k 63 2 k 64 2 k 65 2 k 66 2 ] [ u 2 v 2 u 3 v 3 u 4 v 4 ] = [ p x 2 2 p y 2 2 p x 3 2 p y 3 2 p x 4 2 p y 4 2 ] (1-70) \begin{aligned} \begin{bmatrix} k^1_{11} & k^1_{12} & k^1_{13} & k^1_{14} & k^1_{15} & k^1_{16}\\ k^1_{21} & k^1_{22} & k^1_{23} & k^1_{24} & k^1_{25} & k^1_{26}\\ k^1_{31} & k^1_{32} & k^1_{33} & k^1_{34} & k^1_{35} & k^1_{36}\\ k^1_{41} & k^1_{42} & k^1_{43} & k^1_{44} & k^1_{45} & k^1_{46}\\ k^1_{51} & k^1_{52} & k^1_{53} & k^1_{54} & k^1_{55} & k^1_{56}\\ k^1_{61} & k^1_{62} & k^1_{63} & k^1_{64} & k^1_{65} & k^1_{66} \end{bmatrix}\begin{bmatrix} u_{1}\\ v_{1}\\u_{2}\\ v_{2}\\u_{3}\\ v_{3}\\ \end{bmatrix}=\begin{bmatrix} p^1_{x1}\\ p^1_{y1}\\p^1_{x2}\\ p^1_{y2}\\p^1_{x3}\\ p^1_{y3}\\ \end{bmatrix}\\ \begin{bmatrix} k^2_{11} & k^2_{12} & k^2_{13} & k^2_{14} & k^2_{15} & k^2_{16}\\ k^2_{21} & k^2_{22} & k^2_{23} & k^2_{24} & k^2_{25} & k^2_{26}\\ k^2_{31} & k^2_{32} & k^2_{33} & k^2_{34} & k^2_{35} & k^2_{36}\\ k^2_{41} & k^2_{42} & k^2_{43} & k^2_{44} & k^2_{45} & k^2_{46}\\ k^2_{51} & k^2_{52} & k^2_{53} & k^2_{54} & k^2_{55} & k^2_{56}\\ k^2_{61} & k^2_{62} & k^2_{63} & k^2_{64} & k^2_{65} & k^2_{66} \end{bmatrix}\begin{bmatrix} u_{2}\\ v_{2}\\u_{3}\\ v_{3}\\u_{4}\\ v_{4}\\ \end{bmatrix}=\begin{bmatrix} p^2_{x2}\\ p^2_{y2}\\p^2_{x3}\\ p^2_{y3}\\p^2_{x4}\\ p^2_{y4}\\ \end{bmatrix}\end{aligned}\tag{1-70} k111k211k311k411k511k611k121k221k321k421k521k621k131k231k331k431k531k631k141k241k341k441k541k641k151k251k351k451k551k651k161k261k361k461k561k661 u1v1u2v2u3v3 = px11py11px21py21px31py31 k112k212k312k412k512k612k122k222k322k422k522k622k132k232k332k432k532k632k142k242k342k442k542k642k152k252k352k452k552k652k162k262k362k462k562k662 u2v2u3v3u4v4 = px22py22px32py32px42py42 (1-70)
叠加整理后,整体平衡方程为
[ k 11 1 k 12 1 k 13 1 k 14 1 k 15 1 k 16 1 0 0 k 21 1 k 22 1 k 23 1 k 24 1 k 25 1 k 26 1 0 0 k 31 1 k 32 1 k 33 1 + k 11 2 k 34 1 + k 12 2 k 35 1 + k 13 2 k 36 1 + k 14 2 k 15 2 k 16 2 k 41 1 k 42 1 k 43 1 + k 21 2 k 44 1 + k 22 2 k 45 1 + k 23 2 k 46 1 + k 24 2 k 25 2 k 26 2 k 51 1 k 52 1 k 53 1 + k 31 2 k 54 1 + k 32 2 k 55 1 + k 33 2 k 56 1 + k 34 2 k 35 2 k 36 2 k 61 1 k 62 1 k 63 1 + k 41 2 k 64 1 + k 42 2 k 65 1 + k 43 2 k 66 1 + k 44 2 k 45 2 k 46 2 0 0 k 51 2 k 52 2 k 53 2 k 54 2 k 55 2 k 56 2 0 0 k 61 2 k 62 2 k 63 2 k 64 2 k 65 2 k 66 2 ] [ u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 ] = [ p x 1 1 p y 1 1 p x 2 1 + p x 2 2 p y 2 1 + p y 2 2 p x 3 1 + p x 3 2 p y 3 1 + p y 3 2 p x 4 2 p y 4 2 ] (1-71) \begin{bmatrix} k^1_{11} & k^1_{12} & k^1_{13} & k^1_{14} & k^1_{15} & k^1_{16} & 0 & 0\\ k^1_{21} & k^1_{22} & k^1_{23} & k^1_{24} & k^1_{25} & k^1_{26} & 0 & 0\\ k^1_{31} & k^1_{32} & k^1_{33}+k^2_{11} & k^1_{34}+k^2_{12} & k^1_{35}+k^2_{13} & k^1_{36}+k^2_{14} & k^2_{15} & k^2_{16}\\ k^1_{41}& k^1_{42} & k^1_{43}+k^2_{21}& k^1_{44}+k^2_{22}& k^1_{45} +k^2_{23} & k^1_{46}+k^2_{24} & k^2_{25} & k^2_{26}\\ k^1_{51}& k^1_{52}& k^1_{53}+k^2_{31} & k^1_{54}+k^2_{32} & k^1_{55}+k^2_{33} & k^1_{56}+k^2_{34} & k^2_{35} & k^2_{36}\\ k^1_{61}& k^1_{62}& k^1_{63}+k^2_{41} & k^1_{64}+k^2_{42} & k^1_{65}+k^2_{43} & k^1_{66}+k^2_{44} & k^2_{45} & k^2_{46}\\ 0 & 0 & k^2_{51} & k^2_{52} & k^2_{53} & k^2_{54} & k^2_{55} & k^2_{56}\\ 0 & 0 & k^2_{61} & k^2_{62} & k^2_{63} & k^2_{64} & k^2_{65} & k^2_{66} \end{bmatrix}\begin{bmatrix} u_{1}\\ v_{1}\\u_{2}\\ v_{2}\\u_{3}\\ v_{3}\\u_{4}\\ v_{4}\\ \end{bmatrix}=\begin{bmatrix} p^1_{x1}\\ p^1_{y1}\\p^1_{x2}+p^2_{x2}\\ p^1_{y2}+p^2_{y2}\\p^1_{x3}+p^2_{x3}\\ p^1_{y3}+p^2_{y3}\\p^2_{x4}\\ p^2_{y4}\\ \end{bmatrix}\tag{1-71} k111k211k311k411k511k61100k121k221k321k421k521k62100k131k231k331+k112k431+k212k531+k312k631+k412k512k612k141k241k341+k122k441+k222k541+k322k641+k422k522k622k151k251k351+k132k451+k232k551+k332k651+k432k532k632k161k261k361+k142k461+k242k561+k342k661+k442k542k64200k152k252k352k452k552k65200k162k262k362k462k562k662 u1v1u2v2u3v3u4v4 = px11py11px21+px22py21+py22px31+px32py31+py32px42py42 (1-71)
1.2.2.7 处理约束
如果在上例中,假设节点1为约束,那么 u 1 = v 1 = 0 u_1=v_1=0 u1=v1=0,上式变为
[ k 11 1 k 12 1 k 13 1 k 14 1 k 15 1 k 16 1 0 0 k 21 1 k 22 1 k 23 1 k 24 1 k 25 1 k 26 1 0 0 k 31 1 k 32 1 k 33 1 + k 11 2 k 34 1 + k 12 2 k 35 1 + k 13 2 k 36 1 + k 14 2 k 15 2 k 16 2 k 41 1 k 42 1 k 43 1 + k 21 2 k 44 1 + k 22 2 k 45 1 + k 23 2 k 46 1 + k 24 2 k 25 2 k 26 2 k 51 1 k 52 1 k 53 1 + k 31 2 k 54 1 + k 32 2 k 55 1 + k 33 2 k 56 1 + k 34 2 k 35 2 k 36 2 k 61 1 k 62 1 k 63 1 + k 41 2 k 64 1 + k 42 2 k 65 1 + k 43 2 k 66 1 + k 44 2 k 45 2 k 46 2 0 0 k 51 2 k 52 2 k 53 2 k 54 2 k 55 2 k 56 2 0 0 k 61 2 k 62 2 k 63 2 k 64 2 k 65 2 k 66 2 ] [ 0 0 u 2 v 2 u 3 v 3 u 4 v 4 ] = [ R x 1 R y 1 p x 2 1 + p x 2 2 p y 2 1 + p y 2 2 p x 3 1 + p x 3 2 p y 3 1 + p y 3 2 p x 4 2 p y 4 2 ] (1-72) \begin{bmatrix} k^1_{11} & k^1_{12} & k^1_{13} & k^1_{14} & k^1_{15} & k^1_{16} & 0 & 0\\ k^1_{21} & k^1_{22} & k^1_{23} & k^1_{24} & k^1_{25} & k^1_{26} & 0 & 0\\ k^1_{31} & k^1_{32} & k^1_{33}+k^2_{11} & k^1_{34}+k^2_{12} & k^1_{35}+k^2_{13} & k^1_{36}+k^2_{14} & k^2_{15} & k^2_{16}\\ k^1_{41}& k^1_{42} & k^1_{43}+k^2_{21}& k^1_{44}+k^2_{22}& k^1_{45} +k^2_{23} & k^1_{46}+k^2_{24} & k^2_{25} & k^2_{26}\\ k^1_{51}& k^1_{52}& k^1_{53}+k^2_{31} & k^1_{54}+k^2_{32} & k^1_{55}+k^2_{33} & k^1_{56}+k^2_{34} & k^2_{35} & k^2_{36}\\ k^1_{61}& k^1_{62}& k^1_{63}+k^2_{41} & k^1_{64}+k^2_{42} & k^1_{65}+k^2_{43} & k^1_{66}+k^2_{44} & k^2_{45} & k^2_{46}\\ 0 & 0 & k^2_{51} & k^2_{52} & k^2_{53} & k^2_{54} & k^2_{55} & k^2_{56}\\ 0 & 0 & k^2_{61} & k^2_{62} & k^2_{63} & k^2_{64} & k^2_{65} & k^2_{66} \end{bmatrix}\begin{bmatrix} 0\\ 0\\u_{2}\\ v_{2}\\u_{3}\\ v_{3}\\u_{4}\\ v_{4}\\ \end{bmatrix}=\begin{bmatrix} R_{x1}\\ R_{y1}\\p^1_{x2}+p^2_{x2}\\ p^1_{y2}+p^2_{y2}\\p^1_{x3}+p^2_{x3}\\ p^1_{y3}+p^2_{y3}\\p^2_{x4}\\ p^2_{y4}\\ \end{bmatrix}\tag{1-72} k111k211k311k411k511k61100k121k221k321k421k521k62100k131k231k331+k112k431+k212k531+k312k631+k412k512k612k141k241k341+k122k441+k222k541+k322k641+k422k522k622k151k251k351+k132k451+k232k551+k332k651+k432k532k632k161k261k361+k142k461+k242k561+k342k661+k442k542k64200k152k252k352k452k552k65200k162k262k362k462k562k662 00u2v2u3v3u4v4 = Rx1Ry1px21+px22py21+py22px31+px32py31+py32px42py42 (1-72)
其中 R x 1 、 R y 1 R_{x1}、R_{y1} Rx1、Ry1为支反力,将上式化为两个方程
[ k 33 1 + k 11 2 k 34 1 + k 12 2 k 35 1 + k 13 2 k 36 1 + k 14 2 k 15 2 k 16 2 k 43 1 + k 21 2 k 44 1 + k 22 2 k 45 1 + k 23 2 k 46 1 + k 24 2 k 25 2 k 26 2 k 53 1 + k 31 2 k 54 1 + k 32 2 k 55 1 + k 33 2 k 56 1 + k 34 2 k 35 2 k 36 2 k 63 1 + k 41 2 k 64 1 + k 42 2 k 65 1 + k 43 2 k 66 1 + k 44 2 k 45 2 k 46 2 k 51 2 k 52 2 k 53 2 k 54 2 k 55 2 k 56 2 k 61 2 k 62 2 k 63 2 k 64 2 k 65 2 k 66 2 ] [ u 2 v 2 u 3 v 3 u 4 v 4 ] = [ p x 2 1 + p x 2 2 p y 2 1 + p y 2 2 p x 3 1 + p x 3 2 p y 3 1 + p y 3 2 p x 4 2 p y 4 2 ] K ‾ q ‾ e = P ‾ (1-73) \begin{aligned}\begin{bmatrix} k^1_{33}+k^2_{11} & k^1_{34}+k^2_{12} & k^1_{35}+k^2_{13} & k^1_{36}+k^2_{14} & k^2_{15} & k^2_{16}\\ k^1_{43}+k^2_{21}& k^1_{44}+k^2_{22}& k^1_{45} +k^2_{23} & k^1_{46}+k^2_{24} & k^2_{25} & k^2_{26}\\ k^1_{53}+k^2_{31} & k^1_{54}+k^2_{32} & k^1_{55}+k^2_{33} & k^1_{56}+k^2_{34} & k^2_{35} & k^2_{36}\\ k^1_{63}+k^2_{41} & k^1_{64}+k^2_{42} & k^1_{65}+k^2_{43} & k^1_{66}+k^2_{44} & k^2_{45} & k^2_{46}\\ k^2_{51} & k^2_{52} & k^2_{53} & k^2_{54} & k^2_{55} & k^2_{56}\\ k^2_{61} & k^2_{62} & k^2_{63} & k^2_{64} & k^2_{65} & k^2_{66} \end{bmatrix}\begin{bmatrix} u_{2}\\ v_{2}\\u_{3}\\ v_{3}\\u_{4}\\ v_{4}\\ \end{bmatrix}&=\begin{bmatrix} p^1_{x2}+p^2_{x2}\\ p^1_{y2}+p^2_{y2}\\p^1_{x3}+p^2_{x3}\\ p^1_{y3}+p^2_{y3}\\p^2_{x4}\\ p^2_{y4}\\ \end{bmatrix}\\ \overline K \overline q^e&=\overline P \end{aligned}\tag{1-73} k331+k112k431+k212k531+k312k631+k412k512k612k341+k122k441+k222k541+k322k641+k422k522k622k351+k132k451+k232k551+k332k651+k432k532k632k361+k142k461+k242k561+k342k661+k442k542k642k152k252k352k452k552k652k162k262k362k462k562k662 u2v2u3v3u4v4 Kqe= px21+px22py21+py22px31+px32py31+py32px42py42 =P(1-73)
[ k 13 1 k 14 1 k 15 1 k 16 1 k 23 1 k 24 1 k 25 1 k 26 1 ] [ u 2 v 2 u 3 v 3 ] = [ R x 1 R y 1 ] (1-74) \begin{bmatrix} k^1_{13} & k^1_{14} & k^1_{15} & k^1_{16}\\ k^1_{23} & k^1_{24} & k^1_{25} & k^1_{26}\\ \end{bmatrix}\begin{bmatrix} u_{2}\\ v_{2}\\u_{3}\\ v_{3} \end{bmatrix}=\begin{bmatrix} R_{x1}\\ R_{y1}\\ \end{bmatrix}\tag{1-74} [k131k231k141k241k151k251k161k261] u2v2u3v3 =[Rx1Ry1](1-74)
1.2.2.8 求解节点载荷列阵
1.2.2.9 求解位移列阵
最终通过上式求得位移列阵 q ‾ e = K ‾ − 1 ⋅ P ‾ \overline q^e=\overline K^{-1}\cdot \overline P qe=K−1⋅P,再将与 [ u 1 , v 1 ] T = [ 0 , 0 ] T [u_1,v_1]^T=[0,0]^T [u1,v1]T=[0,0]T组装成最终的节点位移列阵 q e \boldsymbol{q^e} qe。
1.2.2.10 计算应力矩阵等
计算得到最终的节点位移列阵 q e \boldsymbol{q^e} qe后通过一系列的回代得到单元内任意位置的位移、应变、应力矩阵,而式(1-74)用来求解约束支反力。
u ( x , y ) = N ( x , y ) ⋅ q e ε ( x , y ) = B ( x , y ) ⋅ q e σ ( x , y ) = S ( x , y ) ⋅ q e (1-75) \begin{aligned} \mathbf u(x,y) =\mathbf N(x,y)\cdot \mathbf q^e\\ \boldsymbol{\varepsilon}(x,y) = \mathbf B(x,y)\cdot \mathbf q^e\\ \boldsymbol{\sigma}(x,y) = \mathbf S(x,y)\cdot \mathbf q^e \end{aligned}\tag{1-75} u(x,y)=N(x,y)⋅qeε(x,y)=B(x,y)⋅qeσ(x,y)=S(x,y)⋅qe(1-75)
相关文章:

【小呆的力学笔记】非线性有限元的初步认识【三】
文章目录 1.2.2 基于最小势能原理的线性有限元一般格式1.2.2.1 离散化1.2.2.2 位移插值1.2.2.3 单元应变1.2.2.4 单元应力1.2.2.5 单元刚度矩阵1.2.2.6 整体刚度矩阵1.2.2.7 处理约束1.2.2.8 求解节点载荷列阵1.2.2.9 求解位移列阵1.2.2.10 计算应力矩阵等 1.2.2 基于最小势能原…...

python计算闰年
这里说明一下:看到网上很多写python计算闰年的,有很多是不同。 有份省级期刊万年历计算公元1-10000年的闰年 算法如下:4000年停闰一次。区别其他算法,有些是3200年停闰一次。 def division(dividend, divisor) -> bool:"…...

聊聊如何使用Js写一个简单的二级联动和三级联动呢?
前言:咳咳哈,大佬说:"这不是有手就行了?"好吧,这里不做过多罗里吧嗦,真的不过多吹,我们在下面直接上代码上注释。 文章目录: 原Js二级联动实现原Js三级联动实现 一、二级…...

IPv4 和 IPv6 的特点、区别以及在互联网中的应用
在当今互联网时代,IP 地址是连接和通信的基础。IPv4(Internet Protocol version 4)和 IPv6(Internet Protocol version 6)是两种常见的 IP 地址版本。IPv4 是最早广泛使用的 IP 地址协议,而 IPv6 则是 IPv4…...
JavaScript处理移动web交互
touch对象和touchevent touch事件 touch对象 每一次发生touch事件时就会产生一个touch对象,类似事件处理函数中的事件对象。 <div class" "><button class"child" style"height: 400px; width: 400px">我是按钮</b…...

4年测试经验,一问三不知,过于离谱...
公司今年要招人,面倒是面了很多测试,但没有一个合适的。一开始想要的就是中级的水准,也没指望来大牛,当然来了更好,提供的薪资在10-20k,来面试的人有很多,但平均水准真的是让人失望。 看简历时很多都写着3…...
二分查找)
Java 与查找算法(2)二分查找
一、二分查找 二分查找,也称折半查找,是一种常见的查找算法。它的思想是将有序数组分成两部分,取中间位置的值与目标值进行比较,如果相等则返回该位置,如果目标值小于中间值,则在左半部分继续查找…...

Java程序设计入门教程--原始类与包装类
包装类 Java语言是一个面向对象的语言,但是Java中的基本数据类型却是不面向对象的,这在实际使用时存在很多的不便。 为了解决这个不足,在设计类时为每个基本数据类型设计了一个对应的类进行代表,这样八个和基本数据类型对应的类统…...

pip安装python库速度慢、失败及超时报错解决办法
背景: 随着人工智能的不断兴起,python作为最接近人工智能的语言,变得越来越流行,人生苦短,python要学起来。之所以越来用的人喜欢学习python和研究Python,除了python本身便于学些、语法简短、面向对象等特点…...

向量数据库
向量数据库可以做哪些事情 存储和索引向量检索相似向量,还具有过滤功能自动将文档转变成向量,所以会自动化分词、向量化、索引等操作 目前存在的向量数据库: 名称github开源协议chromahttps://github.com/chroma-core/chromaApache 2.0Mil…...
leetcode 11.盛最多水的容器
题目描述 跳转到leetocde题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明ÿ…...

都说00后已经躺平了,但是有一说一,该卷的还是卷啊。
这不,三月份春招我们公司来了个00后,工作没两年,跳槽到我们公司起薪20K,都快接近我了。 后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条件不太好&…...
)
牛客网刷题学习SQL(二)
SQL22 统计每个学校的答过题的用户的平均答题数 描述 运营想要了解每个学校答过题的用户平均答题数量情况,请你取出数据。 用户信息表 user_profile,其中device_id指终端编号(认为每个用户有唯一的一个终端),gender指…...

深蓝学院 C++笔记 先导篇章 - 绪论
一、介绍-老师寄语 为什么选择C? 高性能解决问题 二、C推荐书目 1. 基础 《C Primer》,Stanley B. Lippman 等著,王刚、杨巨峰等译 2. 进阶 《Effective C》,Scott Meyers 著,侯捷译。 《More Effective C》&am…...

R7-19 天梯赛团队总分
“天梯赛”的竞赛题目一共有 15 道,分为 3 个梯级: 基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;题目编号相应为L1-X,X取1,2,3,4,5,6,7,8,分别表示基础级的8道题…...

使用 Kotlin 的 Opt-in (选择加入)功能注解API提示当前非稳定API
前言 之前在给公司项目封装库的时候,领导告诉我封装的漂亮一点,等以后公司发展起来了可能需要把这个库提供给第三方接入使用。 此时,就有这么一个问题:某些功能函数使用条件比较苛刻,直接使用可能会出现意想不到的后…...

webpack配置排除打包
webpack配置排除打包 思路 打包时,不要把类似于element-ui第三方的这些包打进来 从网络上,通过url地址直接引入这些包 操作 (1)先找到 vue.config.js, 添加 externals 项,具体如下: config…...

HNU-操作系统OS-ucoreLab系列-感悟
谨以此片篇,献给熬夜的8个晚上,以及逝去的时光。 感悟: 今天结束了所有的Lab实验(2023.6.3),感慨万千。 喜是这个实验终于结束了,悲是其实有好多地方我都没有理解。 应该指出,由于验收的助教学长学姐们的宽容,HNU实际上在验收这一块的要求还是比较低的。 但是这个…...
MySQL运维篇(三)
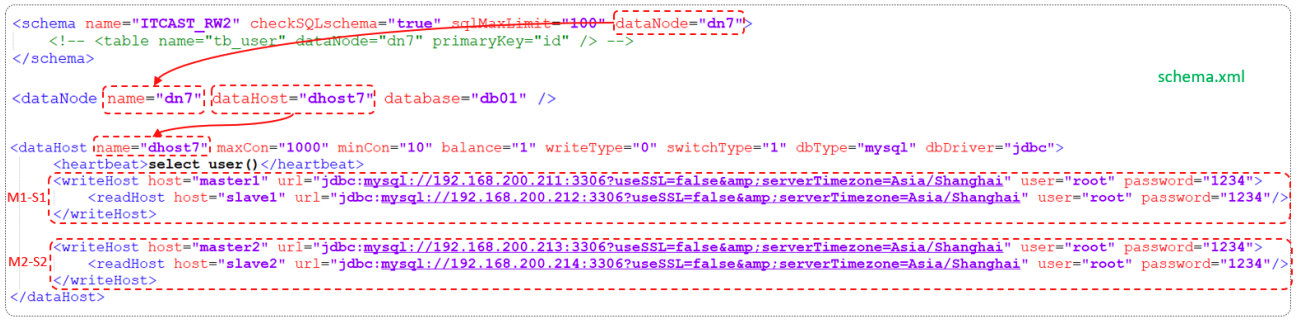
五.读写分离 5.1 介绍 读写分离,简单地说是把对数据库的读和写操作分开,以对应不同的数据库服务器。主数据库提供写操作,从数据库提供读操作,这样能有效地减轻单台数据库的压力。 通过MyCat即可轻易实现上述功能,不仅可以支持MySQL&#x…...

Lecture 2 Text Preprocessing
目录 Some DefinitionsReasons for PreprocessingPreprocessing StepsSentence Segmentation 句子分割Binary Classifier 二元分类器Word Tokenization: English 英文词元标记化Word Tokenization: Chinese 中文词元标记化Word Tokenization: German 德语词元标记化Subword Tok…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
