【枚举算法的Java实现及其应用】
文章目录
- 枚举算法概述
- 枚举算法的实现步骤
- Java实现枚举算法
- 枚举算法的底层工作原理
- 枚举算法的底层代码讲解
- 枚举算法的实际应用场景
- 枚举算法在场景中解决的问题
- 总结
枚举算法概述
枚举算法是一种通过列举所有可能情况来解决问题的方法。这种算法在解决一些特定类型的问题时非常有效,例如素数判断、排列组合等。枚举算法通常具有较低的时间和空间复杂度,但需要较多的计算资源。
枚举算法的实现步骤
- 确定问题:首先明确需要解决的问题是什么,以及问题的输入和输出。
- 列举所有可能情况:根据问题的输入和输出,从所有可能的情况中逐一列举。
- 评估每个可能情况:对于每个列举的情况,评估其解决问题的可行性。
- 选择最优解:根据评估结果,选择最优的可能解。
- 返回结果:将选择的最优解作为问题的解决方案返回。
Java实现枚举算法
以下是一个使用Java实现的素数判断枚举算法示例。
public class PrimeNumber {boolean isPrime(int num) {if (num <= 1) {return false;}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return false;}}return true;}void printPrime(int num) {if (isPrime(num)) {System.out.println(num + " is a prime number");} else {System.out.println(num + " is not a prime number");}}/* Driver method to test above */public static void main(String args[]) {Pri```javaboolean isPrime = isPrime(5);if (isPrime) {printPrime(5);} else {printPrime(6);}}
}
在这个示例中,我们使用了Java的isPrime和printPrime方法来判断一个整数是否为素数。isPrime方法递归地检查整数的因子,直到找到一个小于或等于其平方根的因子。printPrime方法则用于输出判断结果。
枚举算法的底层工作原理
枚举算法的底层原理基于穷举法。穷举法是一种通过遍历所有可能情况来求解问题的方法,它需要逐一检查问题的所有可能解。对于某些问题,枚举算法具有较低的时间和空间复杂度,但在其他问题上可能需要较长的计算时间。
枚举算法的性能取决于问题本身的复杂性。如果问题的解空间较小,枚举算法通常具有较高的时间效率;反之,如果解空间较大,枚举算法可能会消耗大量的计算资源。
枚举算法的底层代码讲解
以下是对上面的isPrime和printPrime方法的Java代码讲解:
// 判断一个整数是否为素数
private boolean isPrime(int num) {if (num <= 1) {return false;}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return false;}}return true;
}
在这个方法中,我们使用一个for循环来遍历所有小于或等于num的因子,并检查它们是否能整除num。如果找到一个因子,则返回false,表示num不是素数;否则,返回true,表示num是素数。
// 输出判断结果
private void printPrime(int num) {if (isPrime(num)) {System.out.println(num + " is a prime number");} else {System.out.println(num + " is not a prime number");}
}
在这个方法中,我们使用isPrime(num)方法的返回值来决定是否输出判断结果。如果isPrime(num)方法返回true,则输出num is a prime number;否则,输出num is not a prime number。
枚举算法的实际应用场景
枚举算法在计算机科学领域的实际应用场景包括:
- 素数判断:判断一个给定的整数是否为素数。
- 组合问题:找出从n个元素中选择m个元素的所有组合。
- 排序算法:在某些特殊情况下,例如对于小规模数据集,可以使用枚举算法实现排序算法。
- 查找算法:查找具有特定属性的元素或特定范围内的元素。
- 图算法:在图中找到从一个顶点到另一个顶点的所有路径。
枚举算法在场景中解决的问题
枚举算法在解决这些实际问题时可以有效地降低问题的复杂性,但在处理大规模数据集时可能会消耗较多的计算资源。枚举算法解决了许多实际问题,例如素数判断、组合问题、排序算法、查找算法和图算法等。在某些特殊情况下,枚举算法可以取得较好的性能,如在处理小规模数据集时。## 枚举算法的优点和缺点
枚举算法具有以下优点:
- 简单易懂:枚举算法的实现相对简单,易于理解和调试。
- 易于调试:由于枚举算法的实现较为直观,因此在调试问题时相对容易找到问题所在。
- 适用于小规模数据集:在处理小规模数据集时,枚举算法通常具有较高的性能,因为计算资源的开销相对较小。
然而,枚举算法也存在以下缺点:
- 时间复杂度较高:对于大规模数据集,枚举算法的时间复杂度较高,可能导致性能下降。
- 空间复杂度较高:在某些情况下,枚举算法可能需要较大的空间来存储计算过程中的中间结果。
- 依赖于输入数据:枚举算法的性能依赖于输入数据的特点。在某些情况下,输入数据的特点可能导致枚举算法的性能较差。
因此,在选择枚举算法时,需要根据问题的规模和输入数据的特点来权衡时间复杂度和空间复杂度。在某些情况下,枚举算法可能是一个可行的解决方案,但在其他情况下,可能需要使用更高效的算法或数据结构。
总结
枚举算法是一种通过列举所有可能情况来解决问题的方法。这种算法在解决一些特定类型的问题时非常有效,例如素数判断、排列组合等。尽管枚举算法在处理大规模数据集时可能具有较高的时间和空间复杂度,但在某些特殊情况下,如处理小规模数据集时,它可能是一个简单易懂且性能较好的解决方案。在实际应用中,需要根据问题的规模和输入数据的特点来权衡枚举算法的优缺点,以确定是否使用这种算法。
相关文章:

【枚举算法的Java实现及其应用】
文章目录 枚举算法概述枚举算法的实现步骤Java实现枚举算法枚举算法的底层工作原理枚举算法的底层代码讲解枚举算法的实际应用场景枚举算法在场景中解决的问题总结 枚举算法概述 枚举算法是一种通过列举所有可能情况来解决问题的方法。这种算法在解决一些特定类型的问题时非常…...

linux led 驱动
前言 今天是儿童节,挣个奖牌给小孩玩玩。 在 linux 驱动大家庭中,LED 驱动算是个儿童,今天就写写他吧。正好之前写过他的婴儿时期《i.MX6ULL 裸机点亮 LED》,记得那时候他还穿着开裆裤呢,裸鸡嘛。 ioremap() 裸机程…...
)
平面最近点对(分治算法)
文章目录 平面最近点对(分治算法)Solution流程完整模板代码 平面最近点对(分治算法) 文章首发于我的个人博客:欢迎大佬们来逛逛 平面最近点对(加强版) - 洛谷 给你一些点,求两点之…...

【基于前后端分离的博客系统】Servlet版本
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一. 项目简介 1. 项目背景 2. 项目用到的技…...

在线Excel绝配:SpreadJS 16.1.1+GcExcel 6.1.1 Crack
前端:SpreadJS 16.1.1 后端: GcExcel 6.1.1 全能 SpreadJS 16.1.1此版本的产品中包含以下功能和增强功能。 添加了各种输入掩码样式选项。 添加了在保护工作表时设置密码以及在取消保护时验证密码的支持。 增强了组合图以将其显示为仪表图。 添加了…...

一个轻量的登录鉴权工具Sa-Token 集成SpringBoot简要步骤
Sa-Token 集成SpringBoot简要步骤 1.1 简单介绍 Sa-Token是一个轻量级Java权限认证框架。 主要解决的问题如下: 登录认证 权限认证 单点登录 OAuth2.0 分布式Session会话 微服务网关鉴权等一系列权限相关问题。 1.2 登录认证 设计思路 对于一些登录之后…...
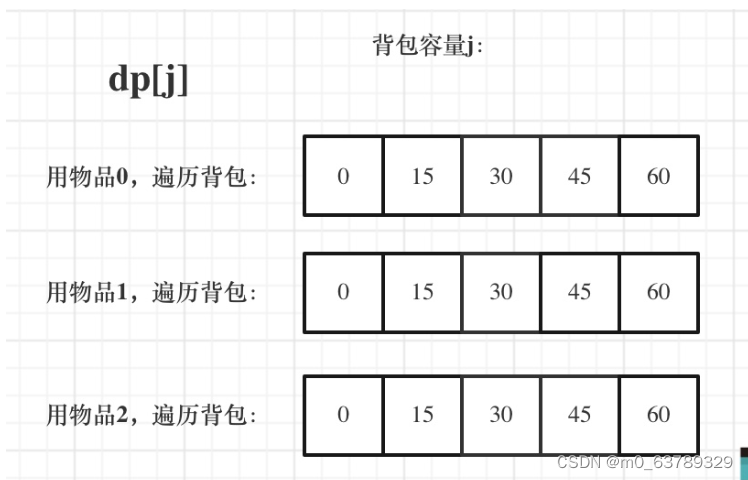
day 44 完全背包:518. 零钱兑换 II;377. 组合总和 Ⅳ
完全背包:物品可以使用多次 完全背包1. 与01背包区别 518. 零钱兑换 II1. dp数组以及下标名义2. 递归公式3. dp数组如何初始化4. 遍历顺序:不能颠倒两个for循环顺序5. 代码 377. 组合总和 Ⅳ:与零钱兑换类似,但是是求组合数1. dp数组以及下标名义2. 递归…...
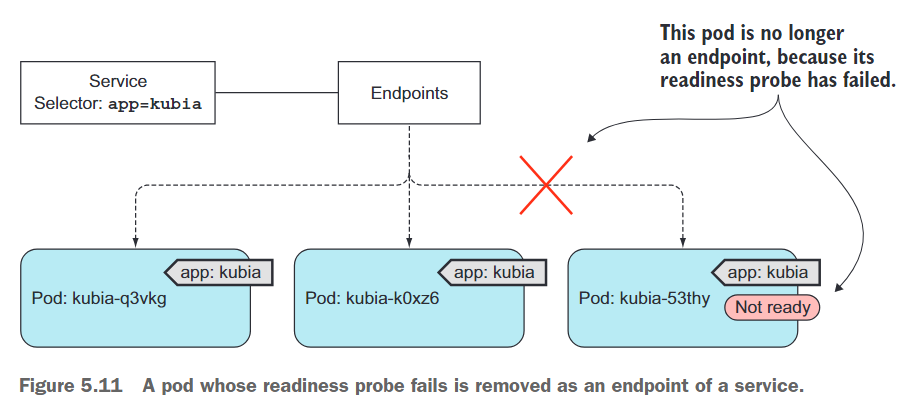
K8s in Action 阅读笔记——【5】Services: enabling clients to discover and talk to pods
K8s in Action 阅读笔记——【5】Services: enabling clients to discover and talk to pods 你已了解Pod以及如何通过ReplicaSets等资源部署它们以确保持续运行。虽然某些Pod可以独立完成工作,但现今许多应用程序需要响应外部请求。例如,在微服务的情况…...

牛客网DAY2(编程题)
圣诞节来啦!请用CSS给你的朋友们制作一颗圣诞树吧~这颗圣诞树描述起来是这样的: 1. "topbranch"是圣诞树的上枝叶,该上枝叶仅通过边框属性、左浮动、左外边距即可实现。边框的属性依次是:宽度为100px、是直线、颜色为gr…...
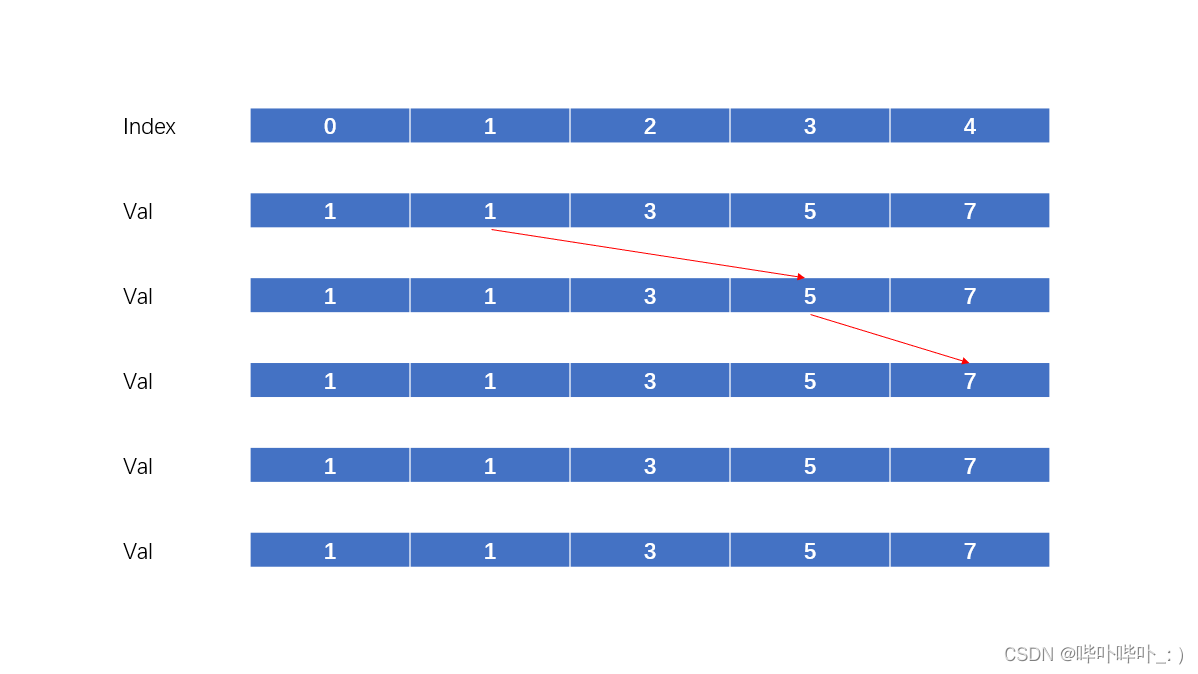
Java经典笔试题—day14
Java经典笔试题—day14 🔎选择题🔎编程题🍭计算日期到天数转换🍭幸运的袋子 🔎结尾 🔎选择题 (1)定义学生、教师和课程的关系模式 S (S#,Sn,Sd,Dc,SA )(其属性分别为学号、姓名、所…...

一个帮助写autoprefixer配置的网站
前端需要用到postcss的工具,用到一个插件叫autoprefixer,这个插件能够给css属性加上前缀,进行一些兼容的工作。 如何安装之类的问题在csdn上搜一下都能找到(注意,vite是包含postcss的,不用在项目中安装pos…...
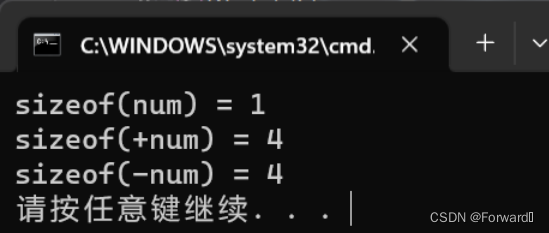
C语言中的类型转换
C语言中的类型转换 隐式类型转换 整型提升 概念: C语言的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的为了获得这个精度,表达式中字符和短整型操作数在使用之前被转换为普通整型,这种转换成为整型提升 如…...
)
String底层详解(包括字符串常量池)
String a “abc”; ,说一下这个过程会创建什么,放在哪里? JVM会使用常量池来管理字符串直接量。在执行这句话时,JVM会先检查常量池中是否已经存有"abc",若没有则将"abc"存入常量池,否…...

C++ 里面lambda和函数指针的转换
问题说明 原始问题,代码如下会编译报错: using DecisionFn bool(*)();class Decide { public:Decide(DecisionFn dec) : _dec{dec} {} private:DecisionFn _dec; };int main() {int x 5;Decide greaterThanThree{ [x](){ return x > 3; } };retur…...

前端Rust开发WebAssembly与Swc插件快速入门
前言 现代前端对速度的追求已经进入二进制工具时代,Rust 开发成为每个人的必修课。 一般我们将常见的前端 Rust 开发分为以下几类,难度由上至下递增: 开发 wasm 。 开发 swc 插件。 开发代码处理工具。 我们将默认读者具备最简单的 Rus…...

【C++ 学习 ⑧】- STL 简介
目录 一、什么是 STL? 二、STL 的版本 三、STL 的 6 大组件和 13 个头文件 四、学习 STL 的 3 个境界 五、STL 的缺陷 参考资料: STL教程:C STL快速入门(非常详细) (biancheng.net)。 C STL是什么,有…...
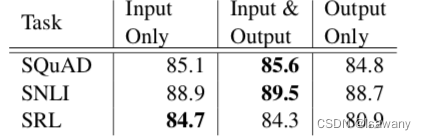
论文笔记--Deep contextualized word representations
论文笔记--Deep contextualized word representations 1. 文章简介2. 文章概括3 文章重点技术3.1 BiLM(Bidirectional Language Model)3.2 ELMo3.3 将ELMo用于NLP监督任务 4. 文章亮点5. 原文传送门 1. 文章简介 标题:Deep contextualized word representations作者…...

【MySQL高级篇笔记-性能分析工具的使用 (中) 】
此笔记为尚硅谷MySQL高级篇部分内容 目录 一、数据库服务器的优化步骤 二、查看系统性能参数 三、统计SQL的查询成本:last_query_cost 四、定位执行慢的 SQL:慢查询日志 1、开启慢查询日志参数 2、查看慢查询数目 3、慢查询日志分析工具…...

大学生数学建模题论文
大学生数学建模题论文篇1 浅论高中数学建模与教学设想 论文关键词:数学建模 数学 应用意识 数学建模教学 论文摘要:为增强学生应用数学的意识,切实培养学生解决实际问题的能力,分析了高中数学建模的必要性,并通过对高中…...

论文阅读 —— 滤波激光SLAM
文章目录 FAST-LIO2FAST-LIOIMUR2LIVER3LIVEEKFLINS退化摘要第一句 FAST-LIO2 摘要: 本文介绍了FAST-LIO2:一种快速、稳健、通用的激光雷达惯性里程计框架。 FAST-LIO2建立在高效紧耦合迭代卡尔曼滤波器的基础上,有两个关键的新颖之处&#…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
