代码随想录二刷day20 | 二叉树之 654.最大二叉树 617.合并二叉树 700.二叉搜索树中的搜索 98.验证二叉搜索树
day20
- 654.最大二叉树
- 617.合并二叉树
- 700.二叉搜索树中的搜索
- 98.验证二叉搜索树
654.最大二叉树
题目链接
解题思路: 本题属于构造二叉树,需要使用前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。
- 确定递归函数的参数和返回值
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针。
代码如下:
TreeNode* constructMaximumBinaryTree(vector<int>& nums)
- 确定终止条件
题目中说了输入的数组大小一定是大于等于1的,所以我们不用考虑小于1的情况,那么当递归遍历的时候,如果传入的数组大小为1,说明遍历到了叶子节点了。
那么应该定义一个新的节点,并把这个数组的数值赋给新的节点,然后返回这个节点。 这表示一个数组大小是1的时候,构造了一个新的节点,并返回。
代码如下:
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {node->val = nums[0];return node;
}
- 确定单层递归的逻辑
这里有三步工作
- 先要找到数组中最大的值和对应的下标, 最大的值构造根节点,下标用来下一步分割数组。
代码如下:
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxValueIndex = i;}
}
TreeNode* node = new TreeNode(0);
node->val = maxValue;
- 最大值所在的下标左区间 构造左子树
这里要判断maxValueIndex > 0,因为要保证左区间至少有一个数值。
代码如下:
if (maxValueIndex > 0) {vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);node->left = constructMaximumBinaryTree(newVec);
}
- 最大值所在的下标右区间 构造右子树
判断maxValueIndex < (nums.size() - 1),确保右区间至少有一个数值。
代码如下:
if (maxValueIndex < (nums.size() - 1)) {vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());node->right = constructMaximumBinaryTree(newVec);
}
整体代码如下:
class Solution {
public:TreeNode* constructMaximumBinaryTree(vector<int>& nums) {TreeNode* node = new TreeNode(0);if (nums.size() == 1) {node->val = nums[0];return node;}// 找到数组中最大的值和对应的下标int maxValue = 0;int maxValueIndex = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] > maxValue) {maxValue = nums[i];maxValueIndex = i;}}node->val = maxValue;// 最大值所在的下标左区间 构造左子树if (maxValueIndex > 0) {vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);node->left = constructMaximumBinaryTree(newVec);}// 最大值所在的下标右区间 构造右子树if (maxValueIndex < (nums.size() - 1)) {vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());node->right = constructMaximumBinaryTree(newVec);}return node;}
};617.合并二叉树
题目链接
解题思路:
递归三部曲来解决:
- 确定递归函数的参数和返回值:
首先要合入两个二叉树,那么参数至少是要传入两个二叉树的根节点,返回值就是合并之后二叉树的根节点。
代码如下:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
- 确定终止条件:
因为是传入了两个树,那么就有两个树遍历的节点t1 和 t2,如果t1 == NULL 了,两个树合并就应该是 t2 了(如果t2也为NULL也无所谓,合并之后就是NULL)。
反过来如果t2 == NULL,那么两个数合并就是t1(如果t1也为NULL也无所谓,合并之后就是NULL)。
代码如下:
if (t1 == NULL) return t2; // 如果t1为空,合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1
- 确定单层递归的逻辑:
单层递归的逻辑就比较好写了,这里我们重复利用一下t1这个树,t1就是合并之后树的根节点(就是修改了原来树的结构)。
那么单层递归中,就要把两棵树的元素加到一起。
t1->val += t2->val;
接下来t1 的左子树是:合并 t1左子树 t2左子树之后的左子树。
t1 的右子树:是 合并 t1右子树 t2右子树之后的右子树。
最终t1就是合并之后的根节点。
代码如下:
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
此时前序遍历,完整代码就写出来了,如下:
整体代码如下:
class Solution {
public:TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2; // 如果t1为空,合并之后就应该是t2if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1// 修改了t1的数值和结构t1->val += t2->val; // 中t1->left = mergeTrees(t1->left, t2->left); // 左t1->right = mergeTrees(t1->right, t2->right); // 右return t1;}
};
700.二叉搜索树中的搜索
题目链接
解题思路:
二叉搜索树是一个有序树:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
1.确定递归函数的参数和返回值
递归函数的参数传入的就是根节点和要搜索的数值,返回的就是以这个搜索数值所在的节点。
代码如下:
TreeNode* searchBST(TreeNode* root, int val)
- 确定终止条件
如果root为空,或者找到这个数值了,就返回root节点。
if (root == NULL || root->val == val) return root;
- 确定单层递归的逻辑
看看二叉搜索树的单层递归逻辑有何不同。
因为二叉搜索树的节点是有序的,所以可以有方向的去搜索。
如果root->val > val,搜索左子树,如果root->val < val,就搜索右子树,最后如果都没有搜索到,就返回NULL。
代码如下:
TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;
很多录友写递归函数的时候 习惯直接写 searchBST(root->left, val),却忘了 递归函数还有返回值。
递归函数的返回值是什么? 是 左子树如果搜索到了val,要将该节点返回。 如果不用一个变量将其接住,那么返回值不就没了。
所以要 result = searchBST(root->left, val)。
整体代码如下:
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == NULL || root->val == val) return root;TreeNode* result = NULL;if (root->val > val) result = searchBST(root->left, val);if (root->val < val) result = searchBST(root->right, val);return result;}
};
98.验证二叉搜索树
相关文章:

代码随想录二刷day20 | 二叉树之 654.最大二叉树 617.合并二叉树 700.二叉搜索树中的搜索 98.验证二叉搜索树
day20 654.最大二叉树617.合并二叉树700.二叉搜索树中的搜索98.验证二叉搜索树 654.最大二叉树 题目链接 解题思路: 本题属于构造二叉树,需要使用前序遍历,因为先构造中间节点,然后递归构造左子树和右子树。 确定递归函数的参数…...

python基础知识(十三):numpy库的基本用法
目录 1. numpy的介绍2. numpy库产生矩阵2.1 numpy将列表转换成矩阵2.2 numpy创建矩阵 3. numpy的基础运算4. numpy的基础运算25. 索引 1. numpy的介绍 numpy库是numpy是python中基于数组对象的科学计算库。 2. numpy库产生矩阵 2.1 numpy将列表转换成矩阵 import numpy as …...
线程函数 tp_recv_thread() 源码分析)
【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread() 源码分析
【【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread 源码分析 一、TP 线程函数:tp_recv_thread()二、处理&上报 坐标数据 cypress_read_touch_data()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码…...
Python3数据分析与挖掘建模(13)复合分析-因子关分析与小结
1.因子分析 1.1 探索性因子分析 探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子,从而帮助简化…...
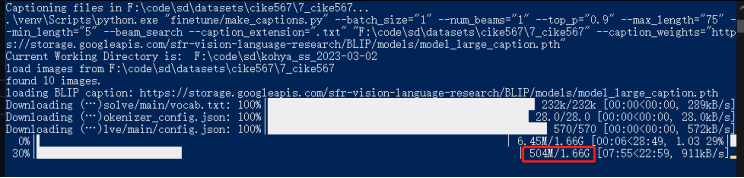
【stable diffusion】图片批量自动打标签、标签批量修改(BLIP、wd14)用于训练SD或者LORA模型
参考: B站教学视频【:AI绘画】新手向!Lora训练!训练集准备、tag心得、批量编辑、正则化准备】官方教程:https://github.com/darkstorm2150/sd-scripts/blob/main/docs/train_README-en.md#automatic-captioning 一、…...

TCP可靠数据传输
TCP的可靠数据传输 1.TCP保证可靠数据传输的方法 TCP主要提供了检验和、序号/确认号、超时重传、最大报文段长度、流量控制等方法实现了可靠数据传输。 检验和 通过检验和的方式,接收端可以检测出来数据是否有差错和异常,假如有差错就会直接丢失该TC…...

Python 私有变量和私有方法介绍
Python 私有变量和私有方法介绍 关于 Python 私有变量和私有方法,通常情况下,开发者可以在方法或属性名称前加上单下划线(_),以表示该方法或属性仅供内部使用,但这只是一种约定,并没有强制执行禁…...
Kotlin Lambda表达式和匿名函数的组合简直太强了
Kotlin Lambda表达式和匿名函数的组合简直太强了 简介 首先,在 Kotlin 中,函数是“第一公民”(First Class Citizen)。因此,它们可以被分配为变量的值,作为其他函数的参数传递或者函数的返回值。同样&…...

uniapp 小程序 获取手机号---通过前段获取
<template><!-- 获取手机号,登录内容 --><view><!-- 首先需要先登录获取code码,然后才可以获取用户唯一标识openid以及会话密钥及用于解密获取手机的加密信息 --><view click"login">登录</view><view…...

面板安全能力持续增强,新增日志审计功能,1Panel开源面板v1.3.0发布
2023年6月12日,现代化、开源的Linux服务器运维管理面板1Panel正式发布v1.3.0版本。 在这一版本中,1Panel进一步增强了安全方面的能力,包括新增SSH配置管理、域名绑定和IP授权支持,以及启用网站防盗链功能。此外,该版本…...
k8s学习-CKS考试必过宝典
目录 CKS考纲集群安装:10%集群强化:15%系统强化:15%微服务漏洞最小化:20%供应链安全:20%监控、日志记录和运行时安全:20% 报名模拟考试考试注意事项考前考中考后 参考 CKS考纲 集群安装:10% 使…...

jmeter如何将上一个请求的结果作为下一个请求的参数
目录 1、简介 2、用途 3、下载、简单应用 4、如何将上一个请求的结果作为下一个请求的参数 1、简介 在JMeter中,可以通过使用变量来将上一个请求的结果作为下一个请求的参数传递。 ApacheJMeter是Apache组织开发的基于Java的压力测试工具。用于对软件做压力测…...

JAVA如何学习爬虫呢?
学习Java爬虫需要掌握以下几个方面: Java基础知识:包括Java语法、面向对象编程、集合框架等。 网络编程:了解HTTP协议、Socket编程等。 HTML、CSS、JavaScript基础:了解网页的基本结构和样式,以及JavaScript的基本语…...

距离保护原理
距离保护是反映故障点至保护安装处的距离,并根据距离的远近确定动作时间的一种保护。故障点距保护安装处越近,保护的动作时间就越短,反之就越长,从而保证动作的选择性。测量故障点至保护安装处的距离,实际上就是用阻抗…...
从微观世界的RST包文视角助力企业网络应用故障排查和优化
1. 前言 随着互联网的普及和发展,各行业的业务和应用越来越依赖于网络。然而,网络环境的不稳定性和复杂性使得出现各种异常现象的概率变得更高了。这些异常现象会导致业务无法正常运行,给用户带来困扰,甚至影响企业的形象和利益。…...

企业微信开发,简单测试。
企业微信开发,参考文档: https://github.com/wechat-group/WxJava/wiki...

element日期选择设置默认时间el-date-picker
<el-date-pickerv-model"rangeDate"style"width:350px"type"daterange"value-format"yyyy-MM-dd"change"dataChange"start-placeholder"开始日期"end-placeholder"结束日期"></el-date-picker…...
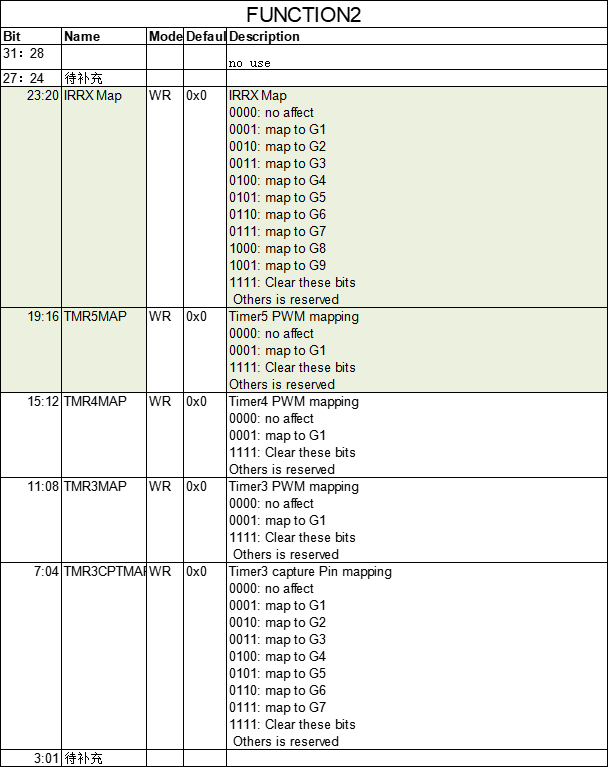
AB32VG:SDK_AB53XX_V061(3)IO口复用功能的补充资料
文章目录 1.IO口功能复用表格2.功能映射寄存器 FUNCTION03.功能映射寄存器 FUNCTION14.功能映射寄存器 FUNCTION2 AB5301A的官方数据手册很不完善,没有开放出来。我通过阅读源码补充了一些关于IO口功能复用寄存器的资料。 官方寄存器文档:《 AB32VG1_Re…...

UnityVR--组件10--UGUI简单介绍
目录 前言 UI基础组件 1. Canvas 2. EventSystem 3. Image 4. Text/TextMeshPro/InputField 5. Button控件 其他 前言 UGUI是Unity推出的新的UI系统,它与Unity引擎结合得更紧密,并拥有强大的屏幕自适应和更简单的深度处理机制,更容易使用和…...
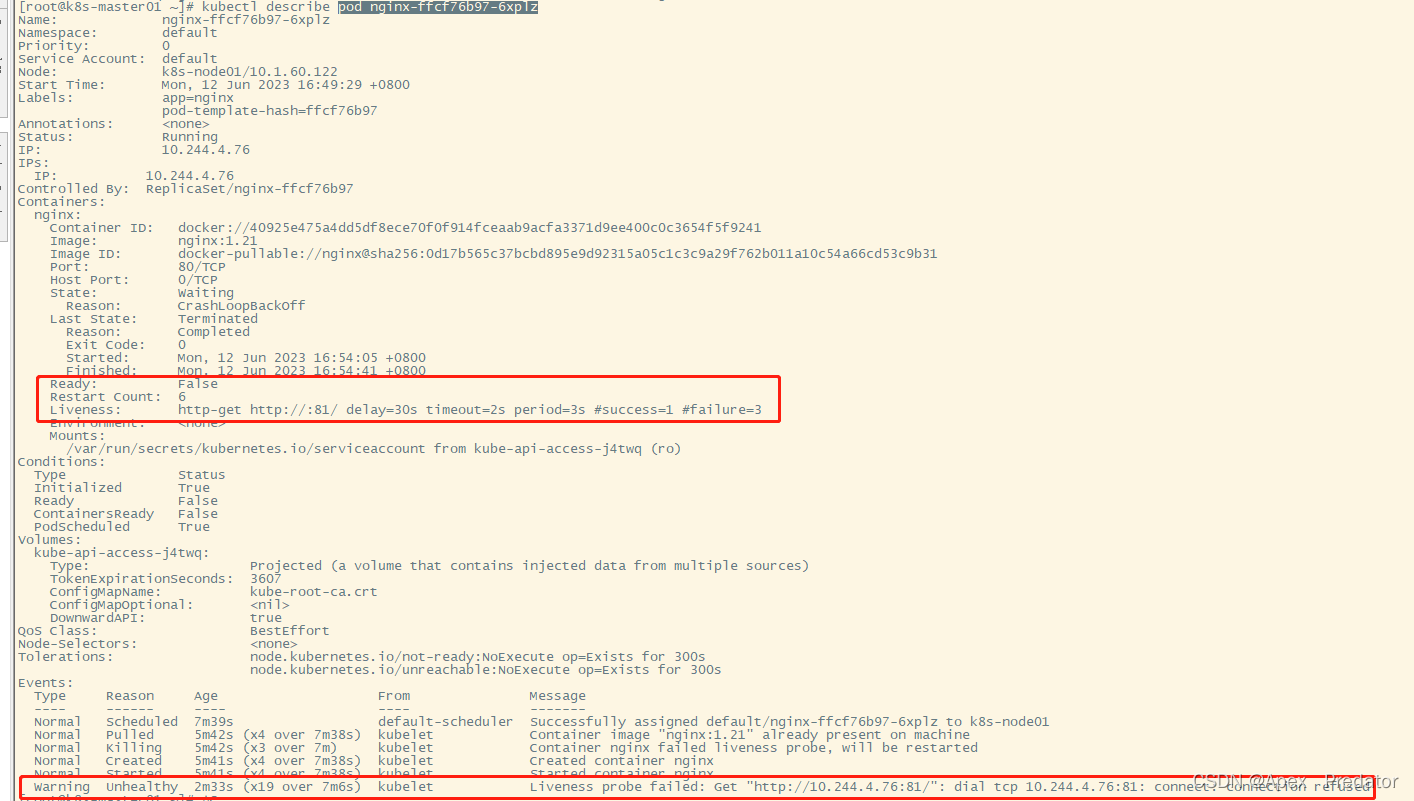
k8s 探针
1.前言 Kubernetes探针(Probe)是用于检查容器运行状况的一种机制。探针可以检查容器是否正在运行,容器是否能够正常响应请求,以及容器内部的应用程序是否正常运行等。在Kubernetes中,探针可以用于确定容器的健康状态,如果容器的健…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
