秋招算法备战第22天 | 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
在一个二叉搜索树中,两个节点 p 和 q 的最近公共祖先可以通过以下的算法找到:
- 从根节点开始。
- 如果当前节点的值大于 p 和 q 的值,那么你需要转向左子树。因为在二叉搜索树中,左子树的所有节点的值都比当前节点的值小。
- 如果当前节点的值小于 p 和 q 的值,那么你需要转向右子树。因为在二叉搜索树中,右子树的所有节点的值都比当前节点的值大。
- 如果以上条件都不满足,那么当前节点就是 p 和 q 的最近公共祖先。
在 Python 中,这个算法可以像这样实现:
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Nonedef lowestCommonAncestor(root, p, q):while root:if root.val > p.val and root.val > q.val:root = root.leftelif root.val < p.val and root.val < q.val:root = root.rightelse:return rootreturn None
在这个代码中,lowestCommonAncestor 函数将接受一个二叉搜索树的根节点 root,和两个需要找最近公共祖先的节点 p 和 q。然后它将返回 p 和 q 的最近公共祖先。如果没有找到,那么它将返回 None。
注意这个算法假设 p 和 q 都在这棵二叉搜索树中。
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
因为是二叉树,直接按照规则遍历,然后在对应叶子结点插入
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if root is None:return TreeNode(val)pre = Nonedef traversal(cur, val, left_child=False):nonlocal preif cur is None:if left_child:pre.left = TreeNode(val)else:pre.right = TreeNode(val)returnpre = curif cur.val > val:traversal(cur.left, val, left_child=True)else:traversal(cur.right, val)traversal(root, val)return root
下面是GPT4对该代码的优化
你的代码已经很好地实现了插入操作。你在遍历树的时候,递归地找到插入节点的位置,然后创建新节点并插入到正确的位置。同时,你用一个外部变量
pre来跟踪上一个节点,以便在正确的位置插入新节点。然而,你的代码可以被优化,使其更简洁和易于理解。在优化后的代码中,你可以使用返回值,而不是外部变量来跟踪插入的位置。这样,你可以避免使用
nonlocal关键字,并使函数的逻辑更加清晰。以下是优化后的代码:# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if root is None:return TreeNode(val)if root.val > val:root.left = self.insertIntoBST(root.left, val)else:root.right = self.insertIntoBST(root.right, val)return root ```在优化后的代码中,插入新节点的逻辑被分配给递归调用的返回值,这使得代码更加简洁并且逻辑更加清晰。这个函数将创建一个新的 `TreeNode` 如果 `root` 是 `None`,否则它将递归地遍历左子树或右子树,根据 `val` 的值决定向哪个方向遍历。然后,递归调用的返回值(即新节点或现有节点)被分配给 `root.left` 或 `root.right`,从而实现插入操作。最后,函数返回 `root`,它现在可能有一个新的子节点。
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
对于二叉搜索树的删除操作,主要分为以下几个步骤:
- 找到需要删除的节点;
- 如果节点是叶子节点,可以直接删除;
- 如果节点只有一个孩子,可以直接将其父节点的相应链接指向它的孩子;
- 如果节点有两个孩子,需要找到其右子树的最小节点(或左子树的最大节点),用这个节点代替要删除的节点,然后删除这个最小(或最大)节点。
以下是一个用Python实现的例子:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = rightclass Solution:def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:if not root:return Noneif key < root.val: # key在左子树root.left = self.deleteNode(root.left, key)elif key > root.val: # key在右子树root.right = self.deleteNode(root.right, key)else: # 找到key,进行删除操作if not root.left: # 左子树为空,直接返回右子树return root.rightif not root.right: # 右子树为空,直接返回左子树return root.leftelse: # 左右子树均不为空min_node = self.findMin(root.right) # 找到右子树的最小节点root.val = min_node.val # 将最小节点的值复制到rootroot.right = self.deleteNode(root.right, min_node.val) # 删除右子树中的最小节点return rootdef findMin(self, node: Optional[TreeNode]) -> Optional[TreeNode]:# 找到树中的最小节点while node.left:node = node.leftreturn node
这个函数的思路主要是使用递归来找到要删除的节点,然后按照上面提到的规则删除。在这个过程中,我们使用了一个辅助函数 findMin 来找到一个树中的最小节点。
总结
今天的题主要是将结点作为返回值,通过遍历过程中更新左右子树来完成对树的操作
相关文章:

秋招算法备战第22天 | 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode) 在一个二叉搜索树中,两个节点 p 和 q 的最近公共祖先可以通过以下的算法找到: 从根节点开始。如果当前节点的值大于 p 和 q 的值,那么你需要转向左子树。因为在二叉…...
小程序之移花宫-自定义底部标签图标---【浅入深出系列005】
浅入深出系列总目录在000集 如何0元学微信小程序–【浅入深出系列000】 不会导入/打开小程序的看这里 让别人的小程序长成自己的样子-更换window上下颜色–【浅入深出系列001】 文章目录 本系列校训学习资源的选择 学习目标图标的注意事项图标资源打开小程序动手实践找到图标最…...
题目1 SQL注入(保姆级教程)
url:http://192.168.154.253:81/ #打开http://XXX:81/,XXX为靶机的ip地址 审题 1、打开题目看到有一个提示,此题目需要通过SQL注入漏洞读取/tmp/360/key文件,key在这个文件中 2、开始答题 发现这里url中有一个id的参数࿰…...
PDF转换成word乱码了怎么办?最实用的方法在这里!
在日常办公中,我们常常需要将PDF文件转换成Word文件,以便于编辑和修改。然而有时候在PDF转Word的过程中可能会遇到乱码的问题,让人感到困扰。在面对这种情况时,我们需要选择正确的方法,避免文件转换后出现乱码。下面我…...

字节跳动后端面试,笔试部分
var code "7022f444-ded0-477c-9afe-26812ca8e7cb" 背景 笔者在刷B站的时候,看到了一个关于面试的实录,前半段是八股文,后半段是笔试部分,感觉笔试部分的题目还是挺有意思的,特此记录一下。 笔试部分 问…...

[JavaScript游戏开发] 2D二维地图绘制、人物移动、障碍检测
系列文章目录 第一章 2D二维地图绘制、人物移动、障碍检测 第二章 跟随人物二维动态地图绘制、自动寻径、小地图显示(人物红点显示) 文章目录 系列文章目录前言一、列计划1.1、目标1.2、步骤 二、使用步骤2.1、准备素材(图片):草坪、人物(熊猫)、障碍(石头)2.2、初…...
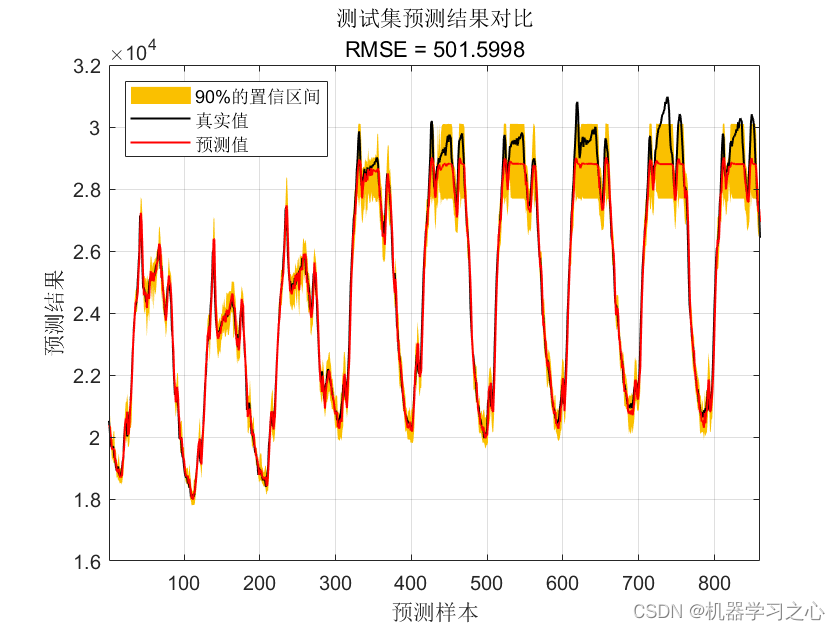
区间预测 | MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型
区间预测 | MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型 目录 区间预测 | MATLAB实现基于QRF随机森林分位数回归时间序列区间预测模型效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于QRF随机森林分位数回归时间序列区间预测模型࿱…...
.NET网络编程——TCP通信
一、网络编程的基本概念 : 1. 网络 就是将不同区域的电脑连接到一起,组成局域网、城域网或广域网。把分部在不同地理区域的计算机于专门的外部设备用通信线路 互联成一个规模大、功能强的网络系统,从而使众多的计算机可以方便地互相传递信息,…...

【Python机器学习】实验01 Numpy以及可视化回顾
文章目录 一、Numpy的基础知识实验1 生成由随机数组成的三通道图片,分别显示每个维度图片,并将三个通道的像素四周进行填充,分别从上下左右各填充若干数据。 二、Numpy的线性代数运算实验2 请准备一张图片,按照上面的过程进行矩阵…...
vue3-组件中的变化
1. 路由 1. 安装指令:npm i vue-routernext 2. 创建路由:createRouter2. 异步组件(defineAsyncComponent) defineAsyncComponent 是用于定义异步组件的函数。defineAsyncComponent 接受一个工厂函数作为参数,这个工厂…...
认识主被动无人机遥感数据、预处理无人机遥感数据、定量估算农林植被关键性状、期刊论文插图精细制作与Appdesigner应用开发
目录 第一章、认识主被动无人机遥感数据 第二章、预处理无人机遥感数据 第三章、定量估算农林植被关键性状 第四章、期刊论文插图精细制作与Appdesigner应用开发 更多推荐 遥感技术作为一种空间大数据手段,能够从多时、多维、多地等角度,获取大量的…...

数学建模的六个步骤
一、模型准备 了解问题的实际背景,明确其实际意义,掌握对象的各种信息,以数学思路来解释问题的精髓,数学思路贯彻问题的全过程,进而用数学语言来描述问题。要求符合数学理论,符合数学习惯,清晰…...
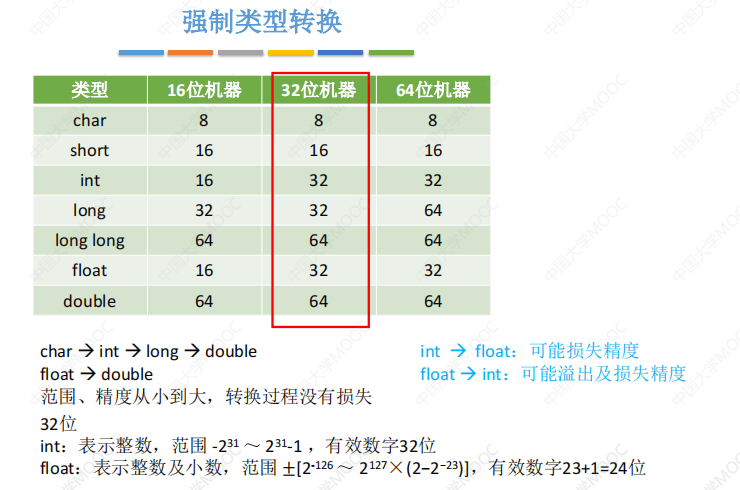
【计算机组成原理】24王道考研笔记——第二章 数据的表示和运算
第二章 数据的表示和运算 一、数值与编码 1.1 进制转换 任意进制->十进制: 二进制<->八进制、十六进制: 各种进制的常见书写方式: 十进制->任意进制:(用拼凑法最快) 真值:符合人…...

JQ-6 Bootstrap入门到实战;Bootstrap的(优缺点、安装、响应式容器原理、网格系统、响应式工具类、Bootstrap组件);小项目实践
目录 1_认识Bootstrap1.1_概念1.2_起源和历史1.3_Bootstrap优缺点 2_Bootstrap4的安装2.1_方式一 CDN2.2_方式二 : 下载源码引入2.3_方式三 : npm安装 3_Bootstrap初体验4_响应式容器原理4.1_屏幕尺寸的分割点(Breakpoints)4.2_响应式容器Containers 5_网…...
如何用3D格式转换工具HOOPS Exchange读取颜色和材料信息?
作为应用程序开发人员,非常希望导入部件的图形表示与它们在创作软件中的外观尽可能接近。外观可以在每个B-Rep面的基础上指定,而且,通过装配层次结构的特定路径可以在视觉外观上赋予父/子覆盖。HOOPS ExchangeHOOPS Exchange可捕获有关来自各…...

[Ubuntu 22.04] 安装docker,并设置镜像加速
for pkg in docker.io docker-doc docker-compose podman-docker containerd runc; do sudo apt-get remove $pkg; doneapt install -y curl vim wget gnupg dpkg apt-transport-https lsb-release ca-certificates# 添加Docker的GPG公钥和apt源 #curl -sSL https://download.d…...
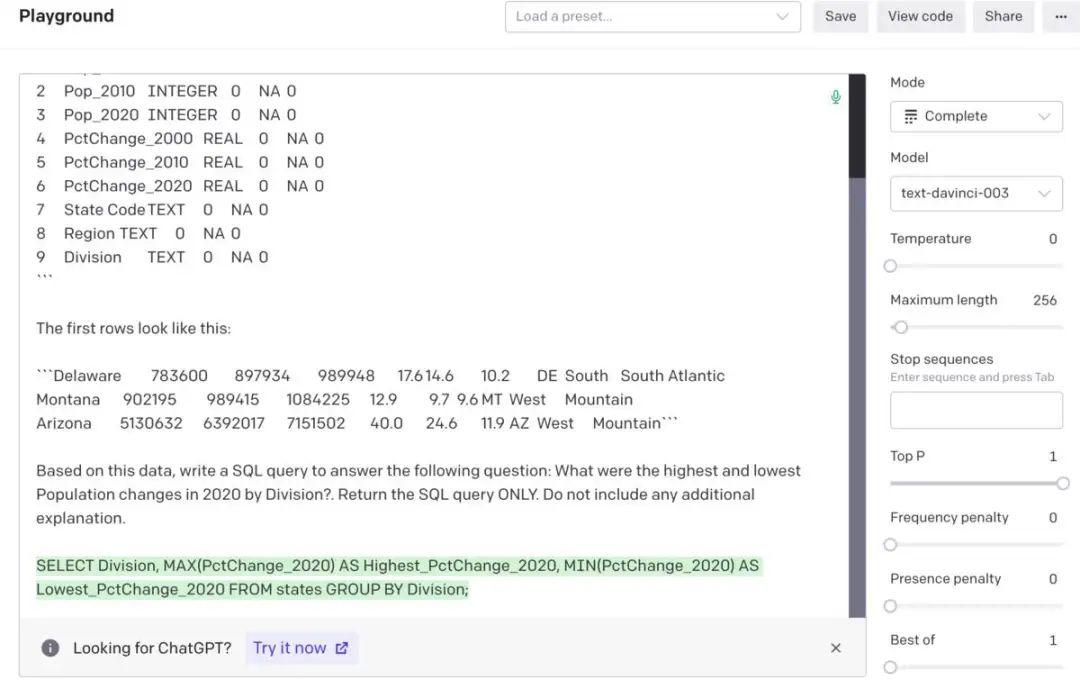
如何使用GPT作为SQL查询引擎的自然语言
生成的AI输出并不总是可靠的,但是下面我会讲述如何改进你的代码和查询的方法,以及防止发送敏感数据的方法。与大多数生成式AI一样,OpenAI的API的结果仍然不完美,这意味着我们不能完全信任它们。幸运的是,现在我们可以…...

Servlet3.0上传文件
页面: <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>文件上传</title> </head> <body> <form action"fileup" enctype"multipart/form-data" method"…...

【ARM Cache 系列文章 6 番外篇 – MMU, MPU, SMMU, PMU 差异与关系】
文章目录 MMU 与 MPU 之间的关系MMU 与 SMMU 之间的关系MMU 与 PMU 之间的关系 上篇文章:ARM Cache 系列文章 5 – 内存屏障ISB/DSB/DMB MMU 与 MPU 之间的关系 MMU(Memory Management Unit)和MPU(Memory Protection Unit&#…...

NetSuite ERP顾问的进阶之路
目录 1.修养篇 1.1“道”是什么?“器”是什么? 1.2 读书这件事儿 1.3 十年计划的力量 1.3.1 一日三省 1.3.2 顾问损益表 1.3.3 阶段课题 2.行为篇 2.1协作 2.2交流 2.3文档管理 2.4时间管理 3.成长篇 3.1概念能力 3.1.1顾问的知识结构 …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
