机器学习笔记【Week2】
一、多变量线性回归(Multivariate Linear Regression)
为什么需要多变量?
现实问题中,一个目标可能受多个因素影响,比如预测房价时:
- x 1 x_1 x1:面积
- x 2 x_2 x2:卧室数量
- x 3 x_3 x3:房龄
- . . . ... ...
假设函数(Hypothesis Function)
在单变量线性回归基础上推广为:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
向量形式更简洁:
h θ ( x ) = θ T x h_\theta(x) = \theta^T x hθ(x)=θTx
其中:
- θ = [ θ 0 , θ 1 , ⋯ , θ n ] T \theta = [\theta_0, \theta_1, \cdots, \theta_n]^T θ=[θ0,θ1,⋯,θn]T(参数向量)
- x = [ 1 , x 1 , x 2 , ⋯ , x n ] T x = [1, x_1, x_2, \cdots, x_n]^T x=[1,x1,x2,⋯,xn]T( x 0 = 1 x_0 = 1 x0=1 以统一偏置项)
模型核心思想:
和单变量回归一样,我们要最小化代价函数:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
然后通过梯度下降法或正规方程法求解。
Python 示例代码(数据模拟)
import numpy as np# 模拟数据:面积、卧室数,房价
X = np.array([[2104, 3],[1600, 3],[2400, 3],[1416, 2],[3000, 4]])
y = np.array([399.9, 329.9, 369.0, 232.0, 539.9]).reshape(-1, 1)m = len(y)# 添加偏置项 x0 = 1
X = np.c_[np.ones((m, 1)), X] # shape = (m, n+1)
theta = np.zeros((X.shape[1], 1)) # 初始参数
二、特征缩放(Feature Scaling)
特征数值差距大时(如面积 [ 50 , 200 ] [50, 200] [50,200] vs 房龄 [ 1 , 30 ] [1, 30] [1,30],梯度下降可能收敛非常慢,因此需要对输入进行缩放。
方法:均值归一化(mean normalization)
x i : = x i − μ i s i x_i := \frac{x_i - \mu_i}{s_i} xi:=sixi−μi
- μ i \mu_i μi:第 i i i 个特征的平均值
- s i s_i si:标准差或最大最小差
使得所有特征都落在类似于 [ − 1 , 1 ] [-1, 1] [−1,1] 范围内
Python 实现:
def feature_normalize(X):mu = np.mean(X, axis=0)sigma = np.std(X, axis=0)X_norm = (X - mu) / sigmareturn X_norm, mu, sigma# 只对 x1~xn 归一化,排除 x0
X[:, 1:], mu, sigma = feature_normalize(X[:, 1:])
三、向量化梯度下降(Vectorized Gradient Descent)
成本函数:
J ( θ ) = 1 2 m ( X θ − y ) T ( X θ − y ) J(\theta) = \frac{1}{2m}(X\theta - y)^T(X\theta - y) J(θ)=2m1(Xθ−y)T(Xθ−y)
梯度公式(向量化):
θ : = θ − α m X T ( X θ − y ) \theta := \theta - \frac{\alpha}{m} X^T(X\theta - y) θ:=θ−mαXT(Xθ−y)
其中:
- X X X 是 m × ( n + 1 ) m \times (n+1) m×(n+1) 的训练样本矩阵
- y y y 是 m × 1 m \times 1 m×1 的目标值列向量
Python 实现:
def compute_cost(X, y, theta):m = len(y)return (1 / (2 * m)) * np.sum((X @ theta - y) ** 2)def gradient_descent(X, y, theta, alpha, num_iters):m = len(y)J_history = []for _ in range(num_iters):error = X @ theta - ygradient = (1 / m) * X.T @ errortheta -= alpha * gradientJ_history.append(compute_cost(X, y, theta))return theta, J_history
四、梯度下降的收敛性分析
如何判断收敛?
- 绘制 J ( θ ) J(\theta) J(θ) 随迭代次数的变化图
- 若代价函数持续下降 → 收敛良好
- 若 震荡 / 上升 → 学习率 α \alpha α 太大,需调小
调整学习率建议:
| 现象 | 原因 | 解决方法 |
|---|---|---|
| 收敛很慢 | 学习率太小 | 增加 α \alpha α |
| 震荡甚至发散 | 学习率太大 | 减小 α \alpha α |
五、正规方程法(Normal Equation)
不使用梯度下降,直接求解析解:
解法公式:
θ = ( X T X ) − 1 X T y \theta = (X^T X)^{-1} X^T y θ=(XTX)−1XTy
Python 实现:
def normal_equation(X, y):return np.linalg.inv(X.T @ X) @ X.T @ ytheta_ne = normal_equation(X, y)
正规方程特点:
| 优点 | 缺点 |
|---|---|
| 不需选择学习率 | 不能用于特征非常多的情况(矩阵求逆开销大) |
| 不需迭代,一次求解 | 对数据量大、特征维度高时效率较低 |
六、可视化训练过程(损失下降)
import matplotlib.pyplot as plttheta, J_history = gradient_descent(X, y, theta, alpha=0.1, num_iters=400)plt.plot(J_history)
plt.xlabel("Iterations")
plt.ylabel("Cost J(θ)")
plt.title("Cost Reduction over Time")
plt.grid(True)
plt.show()
相关文章:

机器学习笔记【Week2】
一、多变量线性回归(Multivariate Linear Regression) 为什么需要多变量? 现实问题中,一个目标可能受多个因素影响,比如预测房价时: x 1 x_1 x1:面积 x 2 x_2 x2:卧室数量 x 3…...
)
饭卡管理系统(接口文档)
一、管理员端口 1、学生列表查询 id(隐藏)姓名性别头像用户名卡号账号余额按钮1小马男http……小马2577293893#C12320.0删除 编辑2小飞男http……小飞#C123 删除 编辑 基本信息 请求路径:/information 请求方式:GET 接口描述&…...

【小白量化智能体】应用2:编写通达信绘图指标及生成Python绘图程序
【小白量化智能体】应用2:编写通达信绘图指标及生成Python绘图程序 【小白量化智能体】是指能够自主或半自主地通过与环境的交互来实现目标或任务的计算实体。智能体技术是一个百科全书,又融合了人工智能、计算机科学、心理学和经济学等多个领域的知识&a…...

C++23 std::start_lifetime_as:用于隐式生存期类型的显式生存期管理函数 (P2590R2)
文章目录 一、C23简介二、std::start_lifetime_as 基本概念函数原型模板参数参数返回值注意事项示例代码 三、std::start_lifetime_as 的作用1. 避免复杂的拷贝操作2. 保持对象表示不变3. 简化代码逻辑 四、std::start_lifetime_as 的使用场景1. 内存池管理2. 类型双关…...

总结:进程和线程的联系和区别
前言:通过学习javaEE初阶中的多线程章节后加上我自己的理解,想来总结一下线程和进程的联系和区别. 一来是能更好地复习知识,二来是为了记录我的学习路程,相信未来的我回首不会忘记这段难忘的经历. 1.进程 先来谈谈进程:进程是操作系统中资源分配的基本单位. 1)进程的执行方…...

Innodb底层原理与Mysql日志机制深入刨析
MySQL的内部组件结构 大体来说,MySQL 可以分为 Server 层和存储引擎层两部分。 Server层 主要包括连接器、查询缓存、分析器、优化器、执行器等,涵盖 MySQL 的大多数核心服务功能,以及所有的内置函数(如日期、时间、数学和加密函数等),所有跨存储引擎的功能都在这一层实…...

JMeter-SSE响应数据自动化
结构图 背景: 需要写一个JMeter脚本来进行自动化测试,主要是通过接口调用一些东西,同时要对响应的数据进行处理,包括不限于错误信息的输出。 1.SSE(摘录) SSE(Server-Sent Events)是一种基于HTTP协议、允许…...

泛型(1)
1.泛型的理解和好处 使用传统方法的问题分析 (1)不能对加入到集合ArrayList中的数据类型进行约束 (2)遍历的时候,需要进行类型装换,如果集合中的数量较大,对效率有影响. 使用泛型的好处 (1)使用泛型添加 (检查元素的类型,提高了安全性.) (2)减少了类型转换的次数,提高效率…...

esp8266 点灯科技远程控制继电器
手机端安装点灯科技app 打开 Arduino IDE 编辑: #define BLINKER_WIFI #include <Blinker.h> char auth[] "点灯科技 key"; char ssid[] "wifi ID"; char pswd[] "WiFi key"; // 新建组件对象 BlinkerButton Button1(&q…...
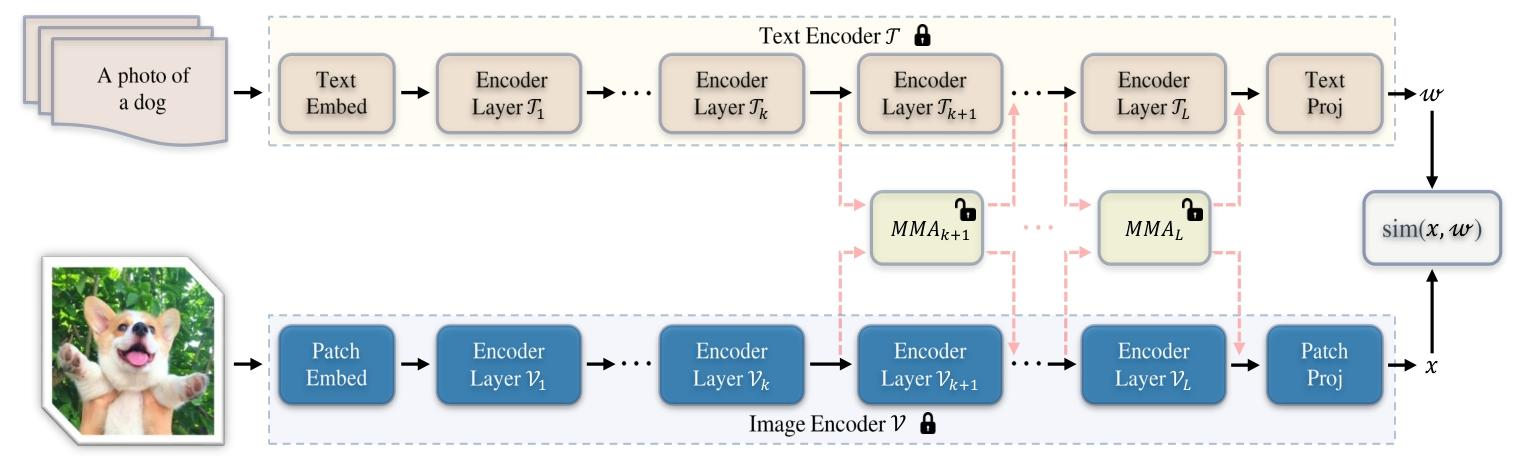
MMA: Multi-Modal Adapter for Vision-Language Models论文解读
abstract 预训练视觉语言模型(VLMs)已成为各种下游任务中迁移学习的优秀基础模型。然而,针对少样本泛化任务对VLMs进行微调时,面临着“判别性—泛化性”困境,即需要保留通用知识,同时对任务特定知识进行微…...

Java中Map集合的遍历方式详解
Java中Map集合的遍历方式详解 一、Map 集合概述二、Map 遍历的基础方式1. **使用 KeySet 迭代器遍历**2. **使用 KeySet 的 for-each 循环** 三、EntrySet 遍历:高效的键值对访问1. **EntrySet 迭代器遍历**2. **EntrySet 的 for-each 循环** 四、Java 8 引入的 Lam…...

使用 Cannonballs 进行实用导体粗糙度建模
在 GB/s 制度下,导体损耗的精确建模是高速串行链路设计成功的前提。未能对粗糙度效果进行建模可能会毁了您的一天。例如,图 1 显示了与测量数据相比,无粗糙度的 40 英寸印刷电路板 (PCB) 走线的模拟总损耗。总损耗是电…...

Spring Boot 注解 @ConditionalOnMissingBean是什么
一句话总结: ConditionalOnMissingBean 是 Spring Boot 提供的一个 条件注解(Conditional Annotation),意思是: 只有当 Spring 容器中 不存在 某个 Bean 时,当前的 Bean 或配置才会被加载。 这是一种典型的…...
)
国外常用支付流程简易说明(无代码)
一、Xendit Xendit 是一家总部位于印度尼西亚的支付解决方案提供商,业务覆盖东南亚多个国家。它允许企业接受信用卡以及多种本地支付方式: 1、如果需要,创建一个 Xendit 帐户并登录Xendit 仪表板。 2、在页面左上角查看您的账户模式。使用…...

(先发再改)测试流程标准文档
Revision Record 修订记录 序号 修改日期 修改章节 修改描述 拟制 审批 修订版本 1 20250520 初稿 v1.0 目录 1. 文档概述... 7 1.1 文档目的... 7 1.1.1 标准化质量保障流程... 7 1.1.2.…...

亚马逊SP-API开发实战:商品数据获取与操作
一、API接入准备 开发者注册: 登录亚马逊开发者中心申请SP-API权限 完成MWS迁移(如适用) 认证配置: # OAuth2.0认证示例 import requests auth_url "https://api.amazon.com/auth/o2/token" params { "…...

行为型:策略模式
目录 1、核心思想 2、实现方式 2.1 模式结构 2.2 实现案例 3、优缺点分析 4、适用场景 5、优化技巧 1、核心思想 目的:将算法(行为)抽象出来作为一系列策略类,使他们可以相互替换,使系统拥有“可插拔”扩展的能…...

知识宇宙-学习篇:开源项目 README 文档该如何写?
名人说:博观而约取,厚积而薄发。——苏轼《稼说送张琥》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、README 文档的重要性1. 项目的第一印象2. 搜索引擎优化的重要载体 二、现代 RE…...

YOLOv12增加map75指标
YOLOv12源码:https://github.com/sunsmarterjie/yolov12 第一步:更改Val.py文件 地址:该文件在yolov12-main\ultralytics\models\yolo\detect下 首先定位到def get_desc(self):这个函数上 代码修正如下: def get_desc(self):&q…...

Avalanche 六期 Workshop 精华合集|Grant 机会、技术深度、项目实战一文回顾!
作为当前区块链技术的前沿代表,Avalanche 以其独特的高吞吐、低延迟、多链架构,为开发者提供了一种颠覆性的 Layer 1 解决方案。不同于传统的 EVM 兼容链,Avalanche 支持开发者自定义执行环境,灵活选择最适合自身业务需求的虚拟机…...

【MySQL】第九弹——索引(下)
文章目录 🌏索引(上)回顾🌏使用索引🪐自动创建索引🪐手动创建索引🚀主键索引🚀普通索引🚀唯一索引🚀复合索引 🪐查看索引🪐删除索引🚀删除主键索引…...

leetcode-295 Find Median from Data Stream
class MaxHeap {private heap: number[];constructor() {this.heap [];}// 插入元素并上浮调整push(num: number): void {this.heap.push(num);this.siftUp(this.heap.length - 1);}// 弹出堆顶元素并下沉调整pop(): number {const top this.heap[0];const last this.heap.p…...

【后端高阶面经:缓存篇】37、高并发系统缓存性能优化:从本地到分布式的全链路设计
一、缓存性能优化的核心价值与分层架构 (一)缓存的多维价值体系 延迟优化 内存访问速度(100ns) vs 磁盘数据库(10ms+),性能提升10万倍+案例:电商详情页通过缓存将响应时间从500ms降至50ms吞吐提升 单机Redis可支撑10万QPS,分担数据库压力案例:秒杀系统通过缓存拦截9…...

西门子 S1500 博途软件舞台威亚 3D 控制方案
西门子 S1500 PLC 是工业自动化领域的主流控制器,适合高精度、高可靠性的舞台威亚控制。下面为你提供基于博途 (TIA Portal) 软件的 3D 控制方案设计。 系统架构设计 舞台威亚 3D 控制系统通常包含以下组件: 硬件层: S1500 PLC 主机伺服驱动…...
)
洛谷 P3374 【模板】树状数组 1(线段树解法)
【题目链接】 洛谷 P3374 【模板】树状数组 1 【题目考点】 1. 线段树 线段树(Segment tree)是一种用来维护区间信息的数据结构。 线段树中每个结点代表一个区间 根结点代表整体区间。 叶子结点代表长为1的单位区间。 对于线段树中的每一个分支结点 [ l , r ] [l, r] [l,r]…...

欣佰特科技| SIL2/PLd 认证 Inxpect毫米波安全雷达:3D 扫描 + 微小运动检测守护工业安全
Inxpect 成立于意大利,专注工业安全技术。自成立起,便致力于借助先进雷达技术提升工业自动化安全标准,解决传统安全设备在复杂环境中的局限,推出获 SIL2/PLd 和 UL 认证的安全雷达产品。 Inxpect 的雷达传感器技术优势明显。相较于…...

大模型量化原理
模型量化的原理是通过降低数值精度来减少模型大小和计算复杂度。让我详细解释其核心原理:我已经为您创建了一个全面的模型量化原理详解文档。总结几个核心要点: 量化的本质 量化的核心是精度换性能的权衡——通过降低数值精度(FP32→INT8&a…...

dify-api的.env配置文件
源码位置:dify\api\.env 本文使用Dify v1.3.1。配置文件中各变量的详细信息表,如下所示: 变量英文名变量中文名默认值变量功能SECRET_KEY秘密密钥XXX用于安全地签署会话cookie的应用秘密密钥。确保在部署时使用强密钥。CONSOLE_API_URL控制…...
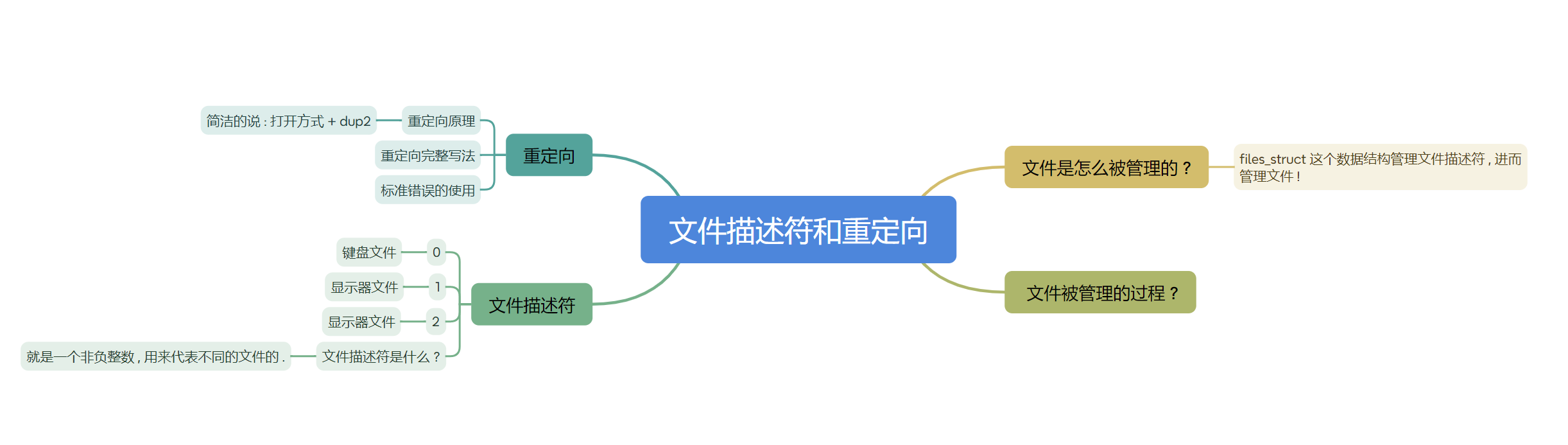
【Linux】Linux 操作系统 - 18 , 重谈文件(二) ~ 文件描述符和重定向原理 , 手把手带你彻底理解 !!!
文章目录 ● 文件描述符一 、Linux 系统对文件的管理(要知道)二 、什么是文件描述符 fd ?三 、再探文件被管理过程(重要)四 、文件描述符 0 、1、21. 文件描述符的分配原则2. 提前认识三个默认打开的文件 ● 重定向原理(重要)一 、重定向现象二 、深入剖析重定向现象(重要)1…...
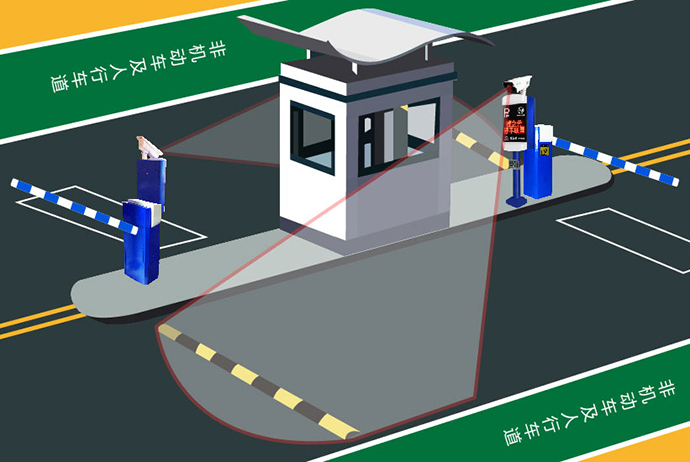
第五十三节:综合项目实践-车牌识别系统
一、项目背景与意义 车牌识别系统(LPR)是智能交通领域的核心技术之一,广泛应用于停车场管理、违章抓拍、高速公路收费等场景。本文将通过Python+OpenCV实现一个完整的车牌识别系统,涵盖图像预处理→车牌定位→字符分割→字符识别四大核心环节。 二、系统架构设计 技术栈组…...
