一起学算法(插入排序篇)
概念:
插入排序(inertion Sort)一般也被称为直接插入排序,是一种简单的直观的排序算法
工作原理:将待排列元素划分为(已排序)和(未排序)两部分,每次从(未排序的)元素选择一个插入到(已排序的)元素中的正确位置,这个位置类似于平时打扑克牌摸牌的操作,右手摸牌,根据牌面的大小放到左手边正确的位置上
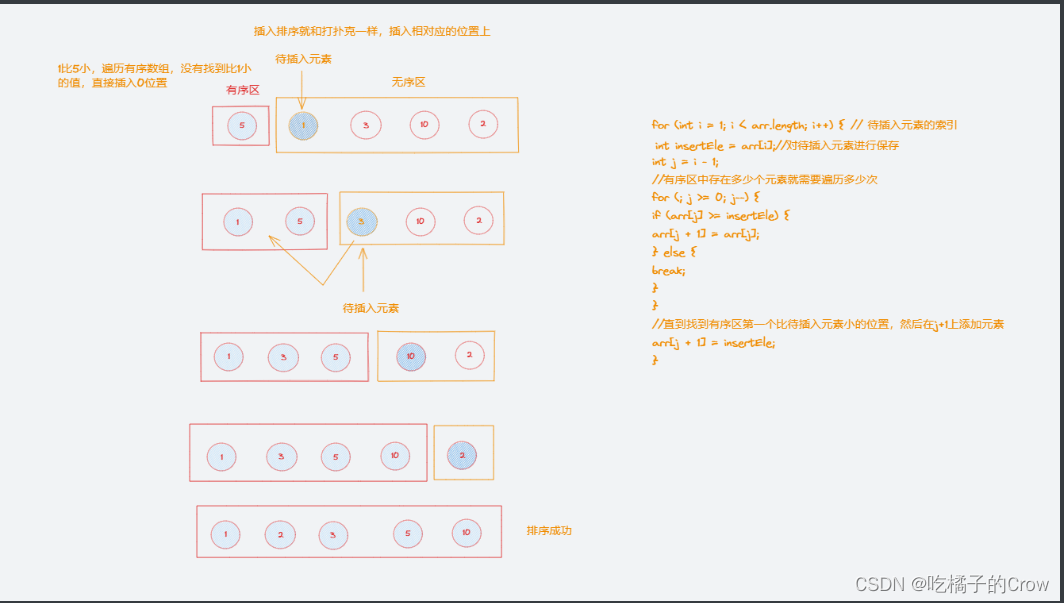
具体实现:使用双层循环,外层循环枚举除了第一个元素之外的所有元素,内层循环遍历当前元素前面的有序表,进行待插入位置查找,并进行移动
public void insertSort(int[] arr) {if (arr == null || arr.length == 0) {return;}for (int i = 1; i < arr.length; i++) { // 待插入元素的索引int insertEle = arr[i];//对待插入元素进行保存int j = i - 1;//有序区中存在多少个元素就需要遍历多少次for (; j >= 0; j--){if (arr[j] >= insertEle) {arr[j + 1] = arr[j];} else {break;}}//直到找到有序区第一个比待插入元素小的位置,然后在j+1上添加元素arr[j + 1] = insertEle;}}leetcode题:
删除某些元素后的数组均值
class Solution {public double trimMean(int[] arr) {if(arr==null||arr.length==0){return 0;}Arrays.sort(arr);int count= arr.length/20;double sum=0;for (int i =count; i < arr.length-count; i++) {sum+=arr[i];}return sum/(arr.length-2*count);}
}去掉最低工资和最高工资后的平均工资
class Solution {public double average(int[] salary) {insertSort(salary);double sum=0;for(int i=1;i<salary.length-1;i++){sum+=salary[i];}return sum/(salary.length-2);}private void insertSort(int[] arr) {if (arr == null || arr.length == 0) {return;}for (int i = 1; i < arr.length; i++) { // 待插入元素的索引int insertEle = arr[i];//对待插入元素进行保存int j = i - 1;//有序区中存在多少个元素就需要遍历多少次for (; j >= 0; j--){if (arr[j] >= insertEle) {arr[j + 1] = arr[j];} else {break;}}//直到找到有序区第一个比待插入元素小的位置,然后在j+1上添加元素arr[j + 1] = insertEle;}}
}学生分数的最小差值
class Solution {//插入排序public void insertSort(int[] nums){if(nums==null||nums.length==0){return;}for (int i =1; i <nums.length; i++) {int insertEle=nums[i];int j=i-1;for(;j>=0;j--){if(nums[j]>=insertEle){nums[j+1]=nums[j];}else{break;}}nums[j+1]=insertEle;}}public int minimumDifference(int[] nums, int k) {if (nums.length == 1) {return 0;}insertSort(nums);int min=nums[k-1]-nums[0];for (int i = 1; i <=nums.length-k; i++) {min=Math.min(min,nums[i+k-1]-nums[i]);}return min;}
}相关文章:

一起学算法(插入排序篇)
概念: 插入排序(inertion Sort)一般也被称为直接插入排序,是一种简单的直观的排序算法 工作原理:将待排列元素划分为(已排序)和(未排序)两部分,每次从&…...
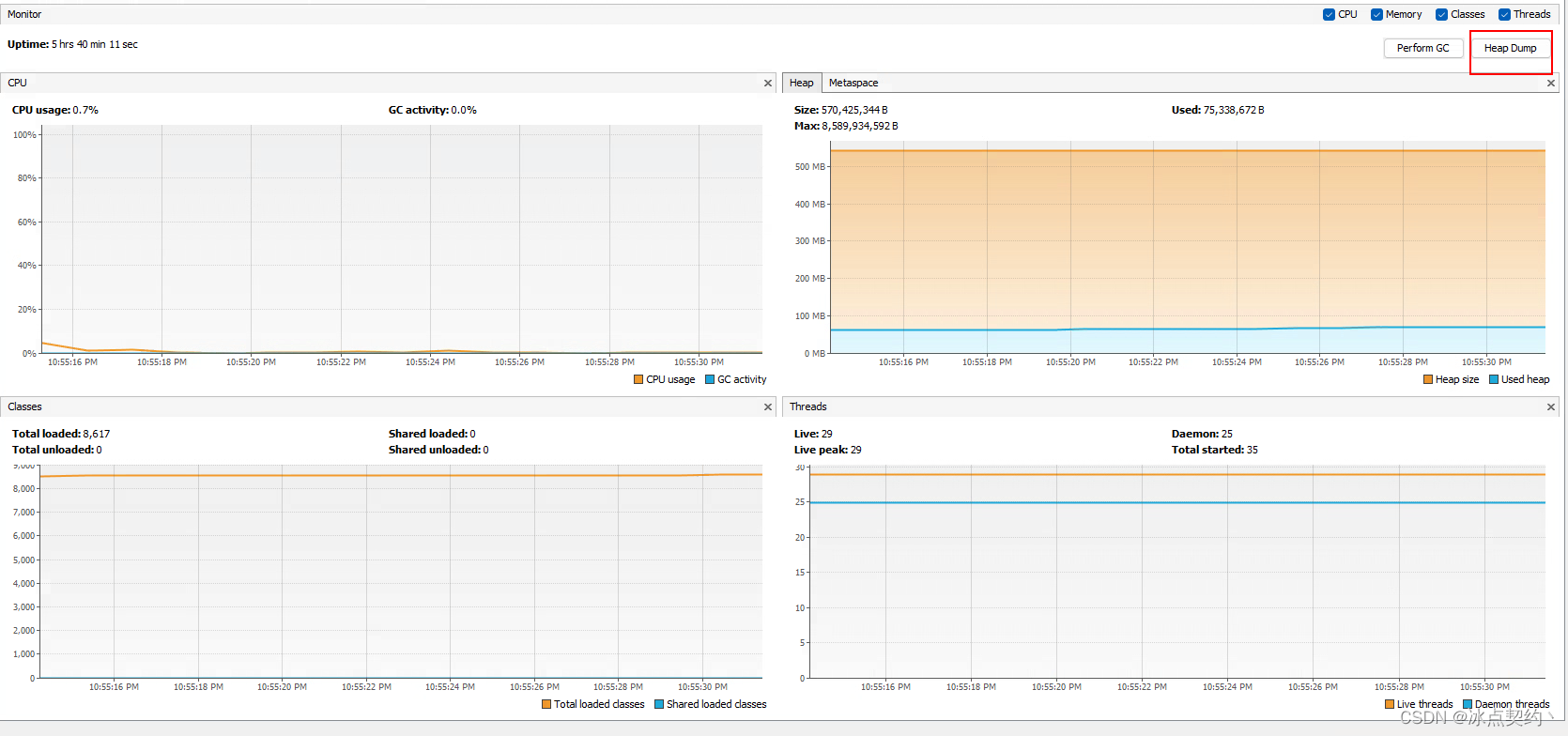
JVM基础篇-本地方法栈与堆
JVM基础篇-本地方法栈与堆 本地方法栈 什么是本地方法? 本地方法即那些不是由java层面实现的方法,而是由c/c实现交给java层面进行调用,这些方法在java中使用native关键字标识 public native int hashCode()本地方法栈的作用? 为本地方法提供内存空…...
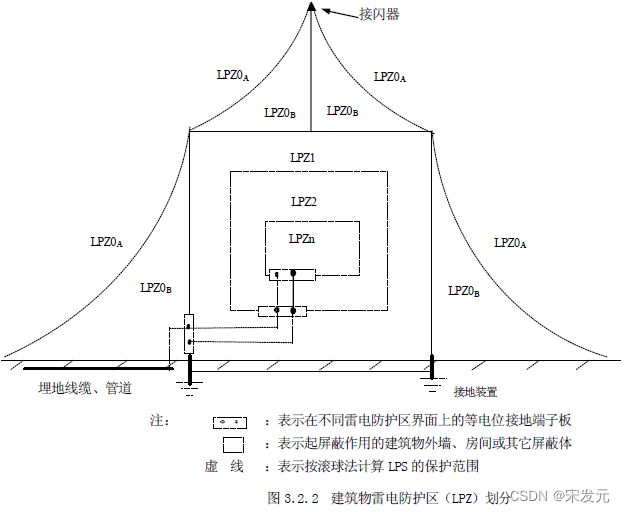
防雷保护区如何划分,防雷分区概念LPZ介绍
在防雷设计中,很重要的一点就是防雷分区的划分,只有先划分好防雷区域等级,才好做出比较好的防雷器设计方案。 因为标准对不同区安装的防雷浪涌保护器要求是不一样的。 那么,防雷保护区是如何划分的呢? 如上图所示&…...

随手笔记——3D−3D:ICP求解
随手笔记——3D−3D:ICP求解 使用 SVD 求解 ICP使用非线性优化来求解 ICP 原理参见 https://blog.csdn.net/jppdss/article/details/131919483 使用 SVD 求解 ICP 使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用 ICP 计算它们的位…...

Python调用各大机器翻译API大全
过去的二三年中,我一直关注的是机器翻译API在自动化翻译过程中的应用,包括采用CAT工具和Python编程语言来调用机器翻译API,然后再进行译后编辑,从而达到快速翻译的目的。 然而,我发现随着人工智能的发展,很…...

重生之我要学C++第六天
这篇文章的主要内容是const以及权限问题、static关键字、友元函数和友元类,希望对大家有所帮助,点赞收藏评论支持一下吧! 更多优质内容跳转: 专栏:重生之C启程(文章平均质量分93) 目录 const以及权限问题 1.const修饰…...

SpringBoot中ErrorPage(错误页面)的使用--【ErrorPage组件】
SpringBoot系列文章目录 SpringBoot知识范围-学习步骤–【思维导图知识范围】 文章目录 SpringBoot系列文章目录本系列校训 SpringBoot技术很多很多环境及工具:必要的知识深层一些的知识 上效果图在Spring Boot里使用ErrorPage还要注意的是 配套资源作业ÿ…...

【Android】APP网络优化学习笔记
网络优化原因 进行网络优化对于移动应用程序而言非常重要,原因如下: 用户体验: 网络连接是移动应用程序的核心功能之一。通过进行网络优化,可以提高应用的加载速度和响应速度,减少用户等待时间,提供更流…...
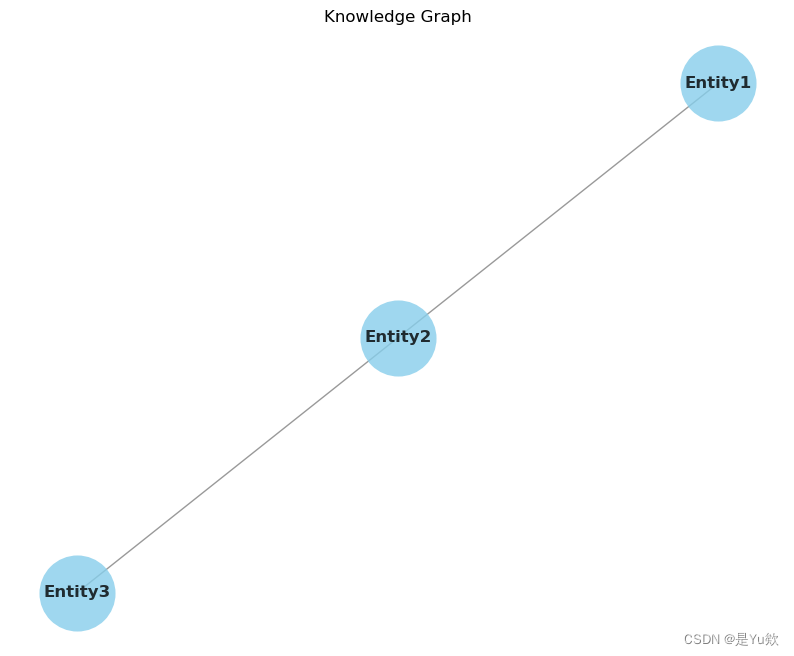
简单的知识图谱可视化+绘制nx.Graph()时报错TypeError: ‘_AxesStack‘ object is not callable
绘制nx.Graph时报错TypeError: _AxesStack object is not callable 写在最前面知识图谱可视化预期报错可能的原因 原代码原因确认解决后的代码解决! 写在最前面 实现一个简单的知识图谱的可视化功能。 使用了NetworkX库来构建知识图谱,并使用matplotlib…...
)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码5.1 fun.m5.2 main.m6.完整代码6.1 fun.m6.2 main.m7.运行结果1.模型原理 基于粒子群优化算法(Particle Swarm Optimization, PSO)优…...
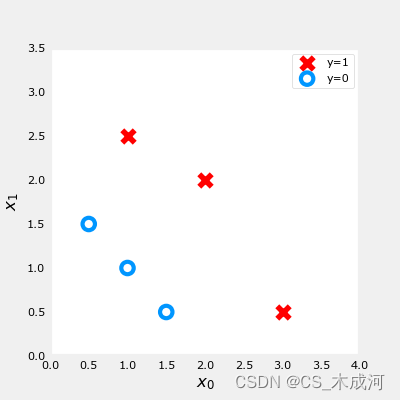
【机器学习】Cost Function for Logistic Regression
Cost Function for Logistic Regression 1. 平方差能否用于逻辑回归?2. 逻辑损失函数loss3. 损失函数cost附录 导入所需的库 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from plt_logistic_loss import plt_logistic_cost, plt_two_…...

【EI/SCOPUS会议征稿】2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)
作为全球科技创新大趋势的引领者,中国一直在为科技创新创造越来越开放的环境,提高学术合作的深度和广度,构建惠及全民的创新共同体。这些努力为全球化和创建共享未来的共同体做出了新的贡献。 为交流近年来国内外在新能源和电气技术领域的最新…...
【计算机网络】10、ethtool
文章目录 一、ethtool1.1 常见操作1.1.1 展示设备属性1.1.2 改变网卡属性1.1.2.1 Auto-negotiation1.1.2.2 Speed 1.1.3 展示网卡驱动设置1.1.4 只展示 Auto-negotiation, RX and TX1.1.5 展示统计1.1.7 排除网络故障1.1.8 通过网口的 LED 区分网卡1.1.9 持久化配置(…...

什么是前端工程化?
工程化介绍 什么是前端工程化? 前端工程化是一种思想,而不是某种技术。主要目的是为了提高效率和降低成本,也就是说在开发的过程中可以提高开发效率,减少不必要的重复性工作等。 tip 现实生活举例 建房子谁不会呢?请…...

【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程
【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程 文章目录 【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程前言确定版本对应关系源码编译安装tiny-cuda-nn总结 前言 本人windows11下使用【Instant Neural Surface Reconstruction】算法时需要…...

Matlab 一种自适应搜索半径的特征提取方法
文章目录 一、简介二、实现代码参考资料一、简介 在之前的博客(C++ ID3决策树)中,提到过一种信息熵的概念,其中它表达的大致意思为:香农认为熵是指“当一件事情有多种可能情况时,这件事情发生某种情况的不确定性”,也就是指如果一个事情的不确定性越大,那么这个信息的熵…...
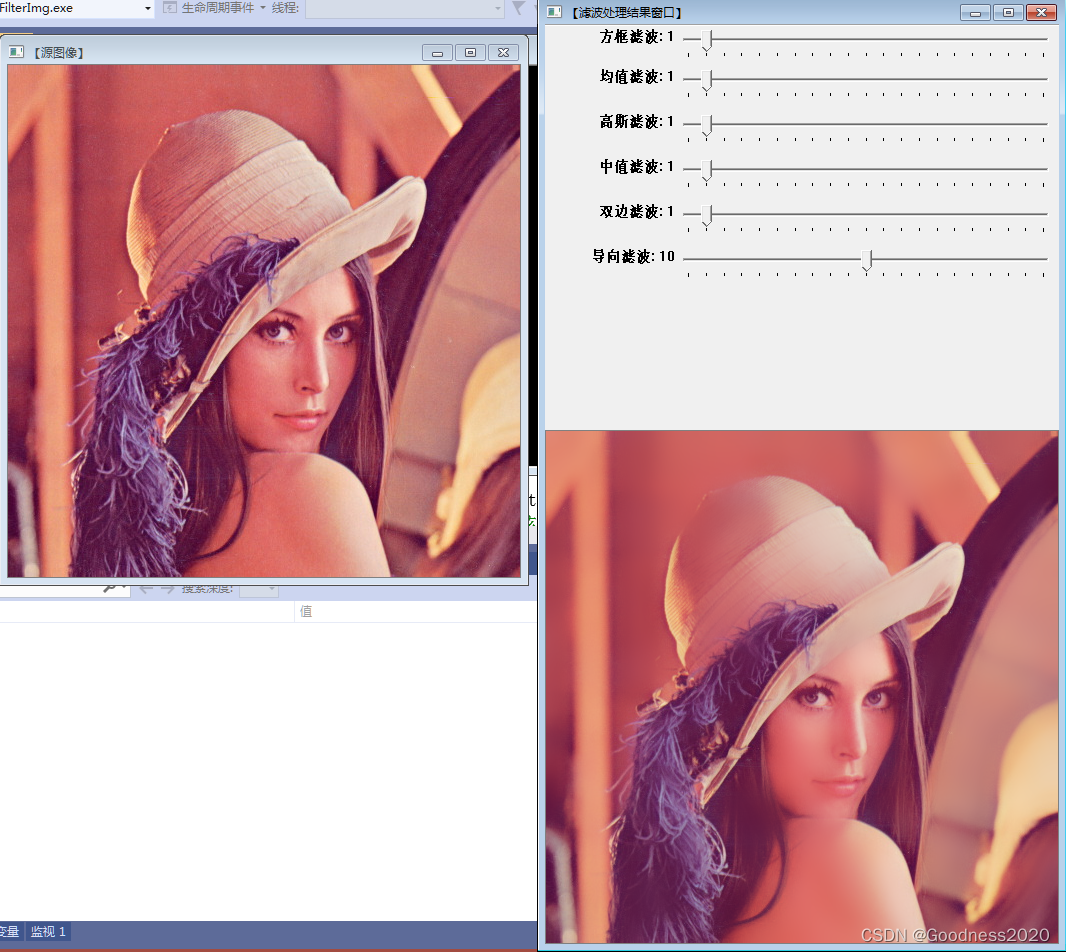
基于opencv的几种图像滤波
一、介绍 盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波、导向滤波。 boxFilter() blur() GaussianBlur() medianBlur() bilateralFilter() 二、代码 #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> …...
puppeteer代理的搭建和配置
puppeteer代理的搭建和配置 本文深入探讨了Puppeteer在网络爬虫和自动化测试中的重要角色,着重介绍了如何搭建和配置代理服务器,以优化Puppeteer的功能和性能。文章首先介绍了Puppeteer作为一个强大的Headless浏览器自动化工具的优势和应用场景…...
【简单认识MySQL的MHA高可用配置】
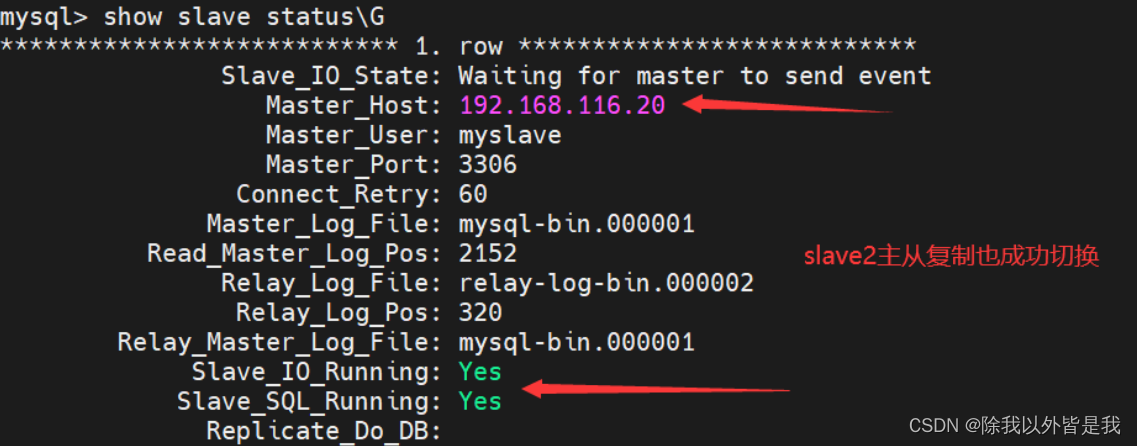
文章目录 一、简介1、概述2、MHA 的组成3.MHA 的特点4、MHA工作原理 二、搭建MHA高可用数据库群集1.主从复制2.MHA配置 三、故障模拟四、故障修复步骤: 一、简介 1、概述 MHA(Master High Availability)是一套优秀的MySQL高可用…...
【云原生】一文学会Docker存储所有特性
目录 1.Volumes 1.Volumes使用场景 2.持久将资源存放 3. 只读挂载 2.Bind mount Bind mounts使用场景 3.tmpfs mounts使用场景 4.Bind mounts和Volumes行为上的差异 5.docker file将存储内置到镜像中 6.volumes管理 1.查看存储卷 2.删除存储卷 3.查看存储卷的详细信息…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
