随手笔记——3D−3D:ICP求解
随手笔记——3D−3D:ICP求解
- 使用 SVD 求解 ICP
- 使用非线性优化来求解 ICP
原理参见 https://blog.csdn.net/jppdss/article/details/131919483
使用 SVD 求解 ICP
使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用 ICP 计算它们的位姿变换。
void pose_estimation_3d3d(const vector<Point3f> &pts1,const vector<Point3f> &pts2,Mat &R, Mat &t) {Point3f p1, p2; // center of massint N = pts1.size();for (int i = 0; i < N; i++) {p1 += pts1[i];p2 += pts2[i];}p1 = Point3f(Vec3f(p1) / N);p2 = Point3f(Vec3f(p2) / N);vector<Point3f> q1(N), q2(N); // remove the centerfor (int i = 0; i < N; i++) {q1[i] = pts1[i] - p1;q2[i] = pts2[i] - p2;}// compute q1*q2^TEigen::Matrix3d W = Eigen::Matrix3d::Zero();for (int i = 0; i < N; i++) {W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();}cout << "W=" << W << endl;// SVD on WEigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);Eigen::Matrix3d U = svd.matrixU();Eigen::Matrix3d V = svd.matrixV();cout << "U=" << U << endl;cout << "V=" << V << endl;Eigen::Matrix3d R_ = U * (V.transpose());if (R_.determinant() < 0) {R_ = -R_;}Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);// convert to cv::MatR = (Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0, 2),R_(1, 0), R_(1, 1), R_(1, 2),R_(2, 0), R_(2, 1), R_(2, 2));t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}
使用非线性优化来求解 ICP
使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用非线性优化计算它们的位姿变换。
/// vertex and edges used in g2o ba
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;virtual void setToOriginImpl() override {_estimate = Sophus::SE3d();}/// left multiplication on SE3virtual void oplusImpl(const double *update) override {Eigen::Matrix<double, 6, 1> update_eigen;update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;}virtual bool read(istream &in) override {}virtual bool write(ostream &out) const override {}
};/// g2o edge
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, VertexPose> {
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}virtual void computeError() override {const VertexPose *pose = static_cast<const VertexPose *> ( _vertices[0] );_error = _measurement - pose->estimate() * _point;}virtual void linearizeOplus() override {VertexPose *pose = static_cast<VertexPose *>(_vertices[0]);Sophus::SE3d T = pose->estimate();Eigen::Vector3d xyz_trans = T * _point;_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);}bool read(istream &in) {}bool write(ostream &out) const {}protected:Eigen::Vector3d _point;
};void bundleAdjustment(const vector<Point3f> &pts1,const vector<Point3f> &pts2,Mat &R, Mat &t) {// 构建图优化,先设定g2otypedef g2o::BlockSolverX BlockSolverType;typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型// 梯度下降方法,可以从GN, LM, DogLeg 中选auto solver = new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));g2o::SparseOptimizer optimizer; // 图模型optimizer.setAlgorithm(solver); // 设置求解器optimizer.setVerbose(true); // 打开调试输出// vertexVertexPose *pose = new VertexPose(); // camera posepose->setId(0);pose->setEstimate(Sophus::SE3d());optimizer.addVertex(pose);// edgesfor (size_t i = 0; i < pts1.size(); i++) {EdgeProjectXYZRGBDPoseOnly *edge = new EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));edge->setVertex(0, pose);edge->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));edge->setInformation(Eigen::Matrix3d::Identity());optimizer.addEdge(edge);}chrono::steady_clock::time_point t1 = chrono::steady_clock::now();optimizer.initializeOptimization();optimizer.optimize(10);chrono::steady_clock::time_point t2 = chrono::steady_clock::now();chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);cout << "optimization costs time: " << time_used.count() << " seconds." << endl;cout << endl << "after optimization:" << endl;cout << "T=\n" << pose->estimate().matrix() << endl;// convert to cv::MatEigen::Matrix3d R_ = pose->estimate().rotationMatrix();Eigen::Vector3d t_ = pose->estimate().translation();R = (Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0, 2),R_(1, 0), R_(1, 1), R_(1, 2),R_(2, 0), R_(2, 1), R_(2, 2));t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}
注:以上仅供个人学习使用,如有侵权,请联系!
相关文章:

随手笔记——3D−3D:ICP求解
随手笔记——3D−3D:ICP求解 使用 SVD 求解 ICP使用非线性优化来求解 ICP 原理参见 https://blog.csdn.net/jppdss/article/details/131919483 使用 SVD 求解 ICP 使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用 ICP 计算它们的位…...

Python调用各大机器翻译API大全
过去的二三年中,我一直关注的是机器翻译API在自动化翻译过程中的应用,包括采用CAT工具和Python编程语言来调用机器翻译API,然后再进行译后编辑,从而达到快速翻译的目的。 然而,我发现随着人工智能的发展,很…...

重生之我要学C++第六天
这篇文章的主要内容是const以及权限问题、static关键字、友元函数和友元类,希望对大家有所帮助,点赞收藏评论支持一下吧! 更多优质内容跳转: 专栏:重生之C启程(文章平均质量分93) 目录 const以及权限问题 1.const修饰…...

SpringBoot中ErrorPage(错误页面)的使用--【ErrorPage组件】
SpringBoot系列文章目录 SpringBoot知识范围-学习步骤–【思维导图知识范围】 文章目录 SpringBoot系列文章目录本系列校训 SpringBoot技术很多很多环境及工具:必要的知识深层一些的知识 上效果图在Spring Boot里使用ErrorPage还要注意的是 配套资源作业ÿ…...

【Android】APP网络优化学习笔记
网络优化原因 进行网络优化对于移动应用程序而言非常重要,原因如下: 用户体验: 网络连接是移动应用程序的核心功能之一。通过进行网络优化,可以提高应用的加载速度和响应速度,减少用户等待时间,提供更流…...
简单的知识图谱可视化+绘制nx.Graph()时报错TypeError: ‘_AxesStack‘ object is not callable
绘制nx.Graph时报错TypeError: _AxesStack object is not callable 写在最前面知识图谱可视化预期报错可能的原因 原代码原因确认解决后的代码解决! 写在最前面 实现一个简单的知识图谱的可视化功能。 使用了NetworkX库来构建知识图谱,并使用matplotlib…...
)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码5.1 fun.m5.2 main.m6.完整代码6.1 fun.m6.2 main.m7.运行结果1.模型原理 基于粒子群优化算法(Particle Swarm Optimization, PSO)优…...
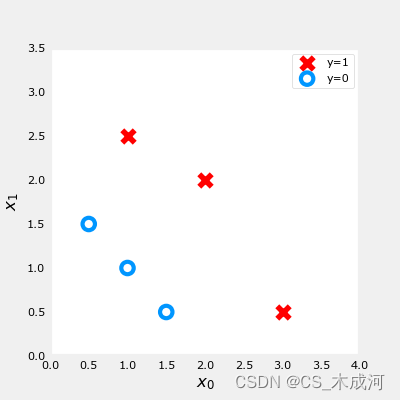
【机器学习】Cost Function for Logistic Regression
Cost Function for Logistic Regression 1. 平方差能否用于逻辑回归?2. 逻辑损失函数loss3. 损失函数cost附录 导入所需的库 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from plt_logistic_loss import plt_logistic_cost, plt_two_…...

【EI/SCOPUS会议征稿】2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)
作为全球科技创新大趋势的引领者,中国一直在为科技创新创造越来越开放的环境,提高学术合作的深度和广度,构建惠及全民的创新共同体。这些努力为全球化和创建共享未来的共同体做出了新的贡献。 为交流近年来国内外在新能源和电气技术领域的最新…...
【计算机网络】10、ethtool
文章目录 一、ethtool1.1 常见操作1.1.1 展示设备属性1.1.2 改变网卡属性1.1.2.1 Auto-negotiation1.1.2.2 Speed 1.1.3 展示网卡驱动设置1.1.4 只展示 Auto-negotiation, RX and TX1.1.5 展示统计1.1.7 排除网络故障1.1.8 通过网口的 LED 区分网卡1.1.9 持久化配置(…...

什么是前端工程化?
工程化介绍 什么是前端工程化? 前端工程化是一种思想,而不是某种技术。主要目的是为了提高效率和降低成本,也就是说在开发的过程中可以提高开发效率,减少不必要的重复性工作等。 tip 现实生活举例 建房子谁不会呢?请…...

【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程
【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程 文章目录 【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程前言确定版本对应关系源码编译安装tiny-cuda-nn总结 前言 本人windows11下使用【Instant Neural Surface Reconstruction】算法时需要…...

Matlab 一种自适应搜索半径的特征提取方法
文章目录 一、简介二、实现代码参考资料一、简介 在之前的博客(C++ ID3决策树)中,提到过一种信息熵的概念,其中它表达的大致意思为:香农认为熵是指“当一件事情有多种可能情况时,这件事情发生某种情况的不确定性”,也就是指如果一个事情的不确定性越大,那么这个信息的熵…...
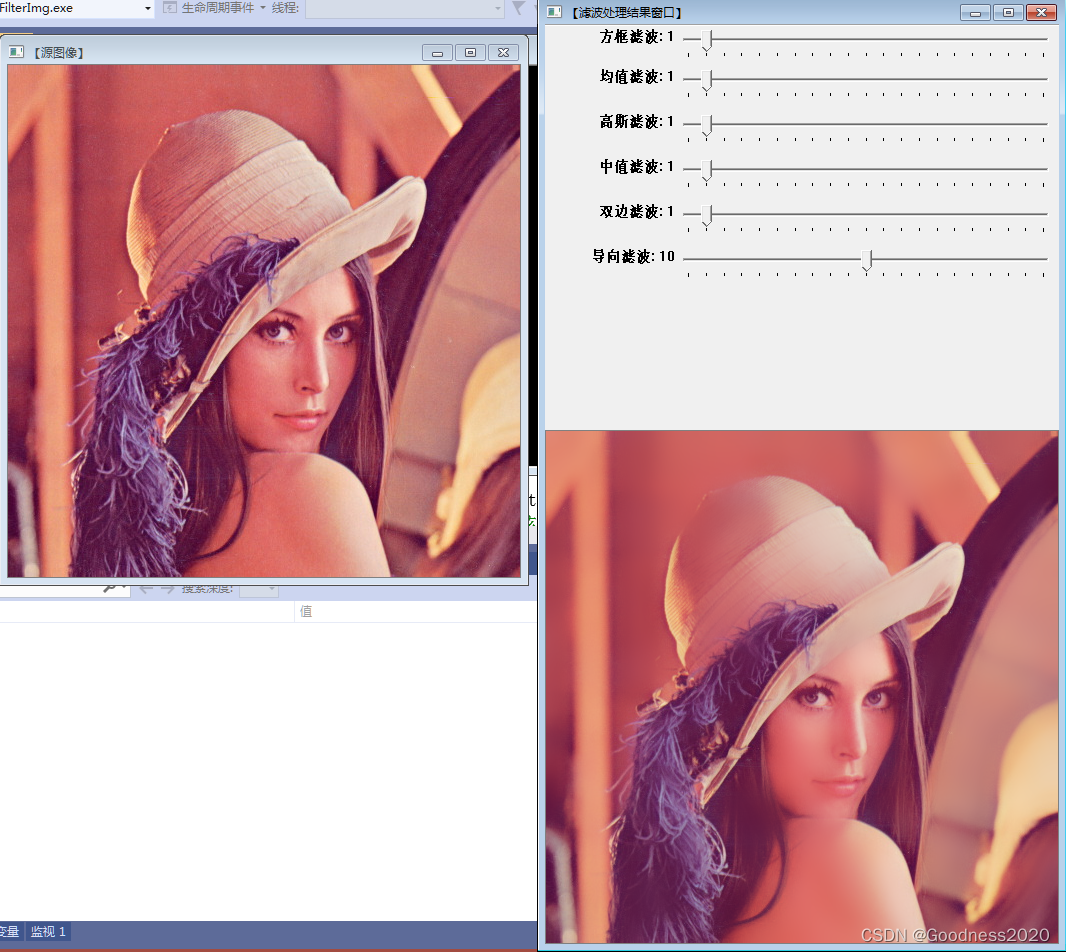
基于opencv的几种图像滤波
一、介绍 盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波、导向滤波。 boxFilter() blur() GaussianBlur() medianBlur() bilateralFilter() 二、代码 #include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> …...
puppeteer代理的搭建和配置
puppeteer代理的搭建和配置 本文深入探讨了Puppeteer在网络爬虫和自动化测试中的重要角色,着重介绍了如何搭建和配置代理服务器,以优化Puppeteer的功能和性能。文章首先介绍了Puppeteer作为一个强大的Headless浏览器自动化工具的优势和应用场景…...
【简单认识MySQL的MHA高可用配置】
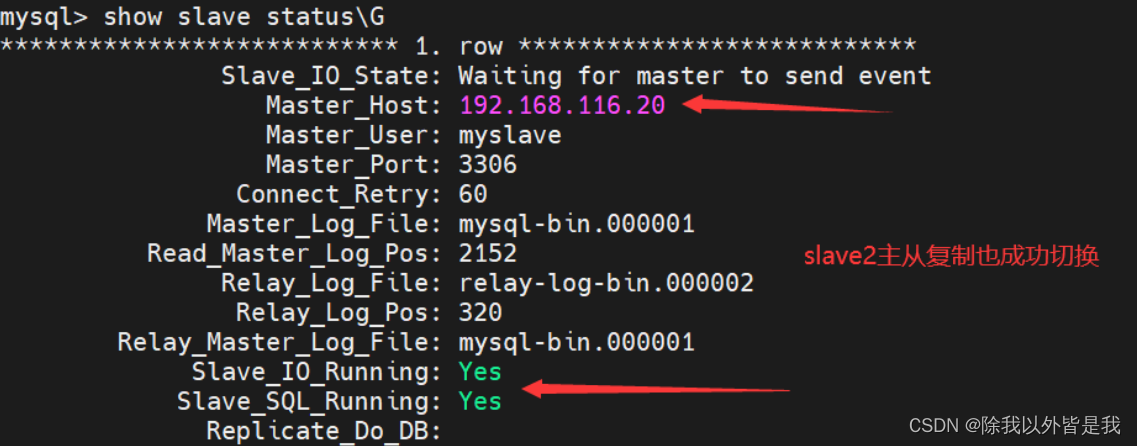
文章目录 一、简介1、概述2、MHA 的组成3.MHA 的特点4、MHA工作原理 二、搭建MHA高可用数据库群集1.主从复制2.MHA配置 三、故障模拟四、故障修复步骤: 一、简介 1、概述 MHA(Master High Availability)是一套优秀的MySQL高可用…...
【云原生】一文学会Docker存储所有特性
目录 1.Volumes 1.Volumes使用场景 2.持久将资源存放 3. 只读挂载 2.Bind mount Bind mounts使用场景 3.tmpfs mounts使用场景 4.Bind mounts和Volumes行为上的差异 5.docker file将存储内置到镜像中 6.volumes管理 1.查看存储卷 2.删除存储卷 3.查看存储卷的详细信息…...

Android Ble蓝牙App(一)扫描
Ble蓝牙App(一)扫描 前言正文一、基本配置二、扫描准备三、扫描页面① 增加UI布局② 点击监听③ 扫描处理④ 广播处理 四、权限处理五、扫描结果① 列表适配器② 扫描结果处理③ 接收结果 六、源码 前言 关于低功耗的蓝牙介绍我已经做过很多了࿰…...
mac pd安装ubuntu并配置远程连接
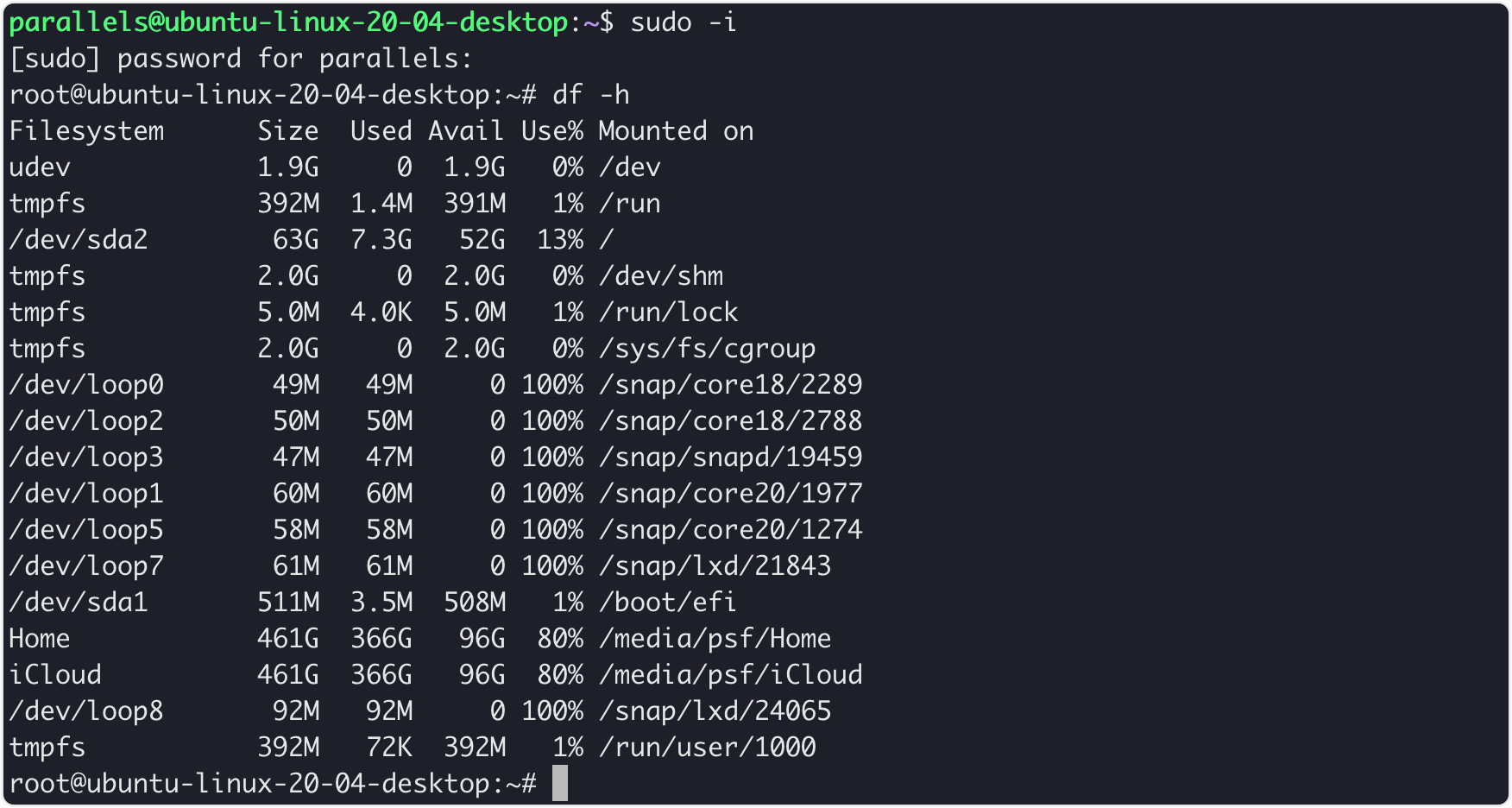
背景 一个安静的下午,我又想去折腾点什么了。准备学习一下k8s的,但是没有服务器。把我给折腾的,在抱怨了:为什么M系列芯片的资源怎么这么少。 好在伙伴说,你可以尝试一下ubantu。于是,我只好在我的mac上安…...
1.3 eureka+ribbon,完成服务注册与调用,负载均衡源码追踪
本篇继先前发布的1.2 eureka注册中心,完成服务注册的内容。 目录 环境搭建 采用eurekaribbon的方式,对多个user服务发送请求,并实现负载均衡 负载均衡原理 负载均衡源码追踪 负载均衡策略 如何选择负载均衡策略? 饥饿加载…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
