二叉树题目:左叶子之和
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:左叶子之和
出处:404. 左叶子之和
难度
3 级
题目描述
要求
给你二叉树的根结点 root \texttt{root} root,返回所有左叶子之和。
示例
示例 1:
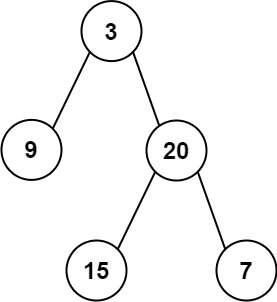
输入: root = [3,9,20,null,null,15,7] \texttt{root = [3,9,20,null,null,15,7]} root = [3,9,20,null,null,15,7]
输出: 24 \texttt{24} 24
解释:二叉树中有两个左叶子,结点值分别是 9 \texttt{9} 9 和 15 \texttt{15} 15。
示例 2:
输入: root = [1] \texttt{root = [1]} root = [1]
输出: 0 \texttt{0} 0
数据范围
- 树中结点数目在范围 [1, 1000] \texttt{[1, 1000]} [1, 1000] 内
- -1000 ≤ Node.val ≤ 1000 \texttt{-1000} \le \texttt{Node.val} \le \texttt{1000} -1000≤Node.val≤1000
解法一
思路和算法
为了计算左叶子之和,需要找到二叉树中的所有是左子结点的叶结点并计算这些结点之和。可以使用深度优先搜索实现。
从根结点开始遍历二叉树,对于每个结点,首先判断其左右子结点是否为空,然后对非空子结点执行如下操作。
-
如果左子结点不为空,当左子结点是叶结点时将左子结点的值加到左叶子之和,当左子结点不是叶结点时在左子树中继续遍历。
-
如果右子结点不为空且不是叶结点,则在右子树中继续遍历。
上述过程是一个递归的过程,递归的终止条件是当前结点为叶结点或者当前结点的非空子结点都为叶结点,其余情况都会调用递归。由于只有在访问到的结点的左子结点是叶结点的情况下才会将左子结点值加到左叶子之和,因此可以确保每个左叶子都被计算一次且其他结点都不会被计算。
代码
class Solution {public int sumOfLeftLeaves(TreeNode root) {int sum = 0;if (root.left != null) {if (isLeaf(root.left)) {sum += root.left.val;} else {sum += sumOfLeftLeaves(root.left);}}if (root.right != null && !isLeaf(root.right)) {sum += sumOfLeftLeaves(root.right);}return sum;}public boolean isLeaf(TreeNode node) {return node.left == null && node.right == null;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
解法二
思路和算法
也可以使用广度优先搜索计算左叶子之和。
广度优先搜索需要使用队列存储待访问的结点,初始时将根结点入队列。每次将一个结点出队列,首先判断其左右子结点是否为空,然后对非空子结点执行如下操作。
-
如果左子结点不为空,当左子结点是叶结点时将左子结点的值加到左叶子之和,当左子结点不是叶结点时将左子结点入队列。
-
如果右子结点不为空且不是叶结点,则将右子结点入队列。
当队列为空时遍历结束,此时即可得到左叶子之和。
由于只有在访问到的结点的左子结点是叶结点的情况下才会将左子结点值加到左叶子之和,因此可以确保每个左叶子都被计算一次且其他结点都不会被计算。
代码
class Solution {public int sumOfLeftLeaves(TreeNode root) {int sum = 0;Queue<TreeNode> queue = new ArrayDeque<TreeNode>();queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();if (node.left != null) {if (isLeaf(node.left)) {sum += node.left.val;} else {queue.offer(node.left);}}if (node.right != null) {if (!isLeaf(node.right)) {queue.offer(node.right);}}}return sum;}public boolean isLeaf(TreeNode node) {return node.left == null && node.right == null;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
相关文章:

二叉树题目:左叶子之和
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:左叶子之和 出处:404. 左叶子之和 难度 3 级 题目描述 要求 给你二叉树的根结点 root \texttt{ro…...

Spark SQL报错: Task failed while writing rows.
错误 今天运行 Spark 任务时报了一个错误,如下所示: WARN scheduler.TaskSetManager: Lost task 9.0 in stage 3.0 (TID 69, xxx.xxx.xxx.com, executor 3): org.apache.spark.SparkException: Task failed while writing rows.at org.apache.spark.sq…...
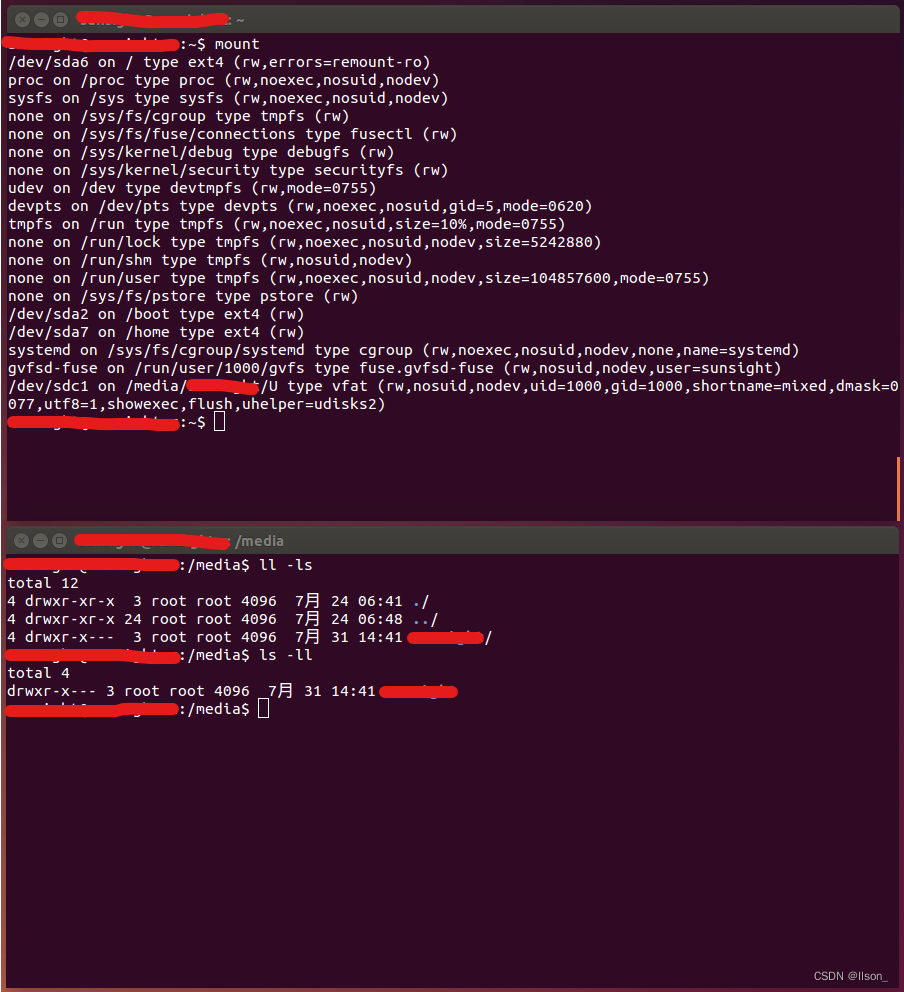
Linux系统下U盘打不开: No application is registered as handling this file
简述 系统是之前就安装好使用的Ubuntu14.04,不过由于某些原因只安装到了机械硬盘中;最近新买了一块固态硬盘,所以打算把Ubuntu系统迁移到新的固态硬盘上; 当成功的迁移了系统之后发现其引导有点问题,导致多个系统启动不…...

07 定时器处理非活动连接(上)
07 定时器处理非活动连接(上) 基础知识 非活跃,是指客户端(这里是浏览器)与服务器端建立连接后,长时间不交换数据,一直占用服务器端的文件描述符,导致连接资源的浪费。 定时事件&a…...
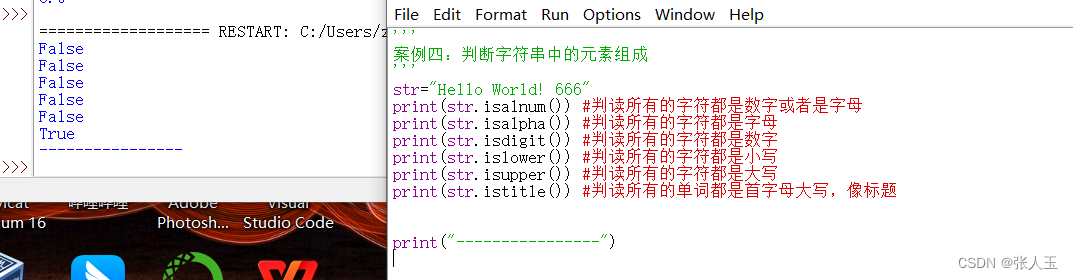
python——案例四:判断字符串中的元素组成
案例四:判断字符串中的元素组成str"Hello World! 666" print(str.isalnum()) #判读所有的字符都是数字或者是字母 print(str.isalpha()) #判读所有的字符都是字母 print(str.isdigit()) #判读所有的字符都是数字 print(str.islower()) #判读所有的字符都是…...
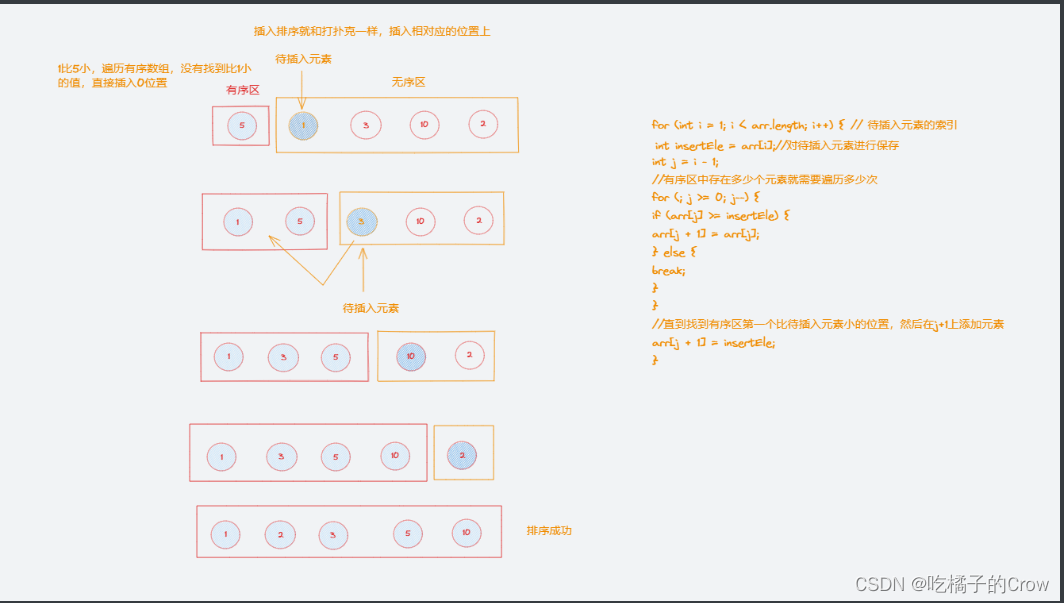
一起学算法(插入排序篇)
概念: 插入排序(inertion Sort)一般也被称为直接插入排序,是一种简单的直观的排序算法 工作原理:将待排列元素划分为(已排序)和(未排序)两部分,每次从&…...
JVM基础篇-本地方法栈与堆
JVM基础篇-本地方法栈与堆 本地方法栈 什么是本地方法? 本地方法即那些不是由java层面实现的方法,而是由c/c实现交给java层面进行调用,这些方法在java中使用native关键字标识 public native int hashCode()本地方法栈的作用? 为本地方法提供内存空…...
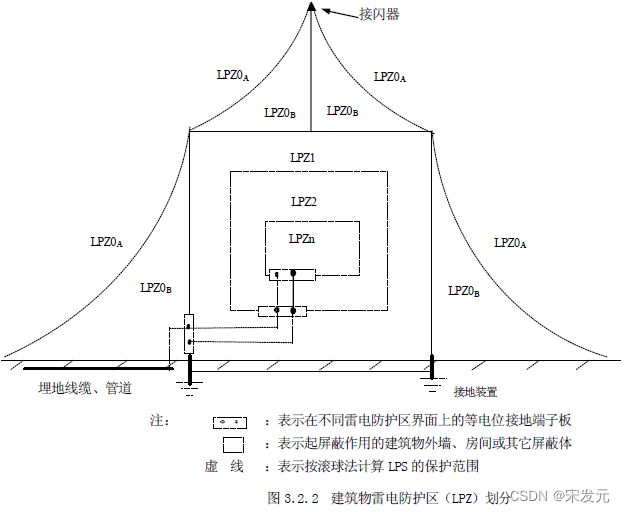
防雷保护区如何划分,防雷分区概念LPZ介绍
在防雷设计中,很重要的一点就是防雷分区的划分,只有先划分好防雷区域等级,才好做出比较好的防雷器设计方案。 因为标准对不同区安装的防雷浪涌保护器要求是不一样的。 那么,防雷保护区是如何划分的呢? 如上图所示&…...

随手笔记——3D−3D:ICP求解
随手笔记——3D−3D:ICP求解 使用 SVD 求解 ICP使用非线性优化来求解 ICP 原理参见 https://blog.csdn.net/jppdss/article/details/131919483 使用 SVD 求解 ICP 使用两幅 RGB-D 图像,通过特征匹配获取两组 3D 点,最后用 ICP 计算它们的位…...

Python调用各大机器翻译API大全
过去的二三年中,我一直关注的是机器翻译API在自动化翻译过程中的应用,包括采用CAT工具和Python编程语言来调用机器翻译API,然后再进行译后编辑,从而达到快速翻译的目的。 然而,我发现随着人工智能的发展,很…...

重生之我要学C++第六天
这篇文章的主要内容是const以及权限问题、static关键字、友元函数和友元类,希望对大家有所帮助,点赞收藏评论支持一下吧! 更多优质内容跳转: 专栏:重生之C启程(文章平均质量分93) 目录 const以及权限问题 1.const修饰…...

SpringBoot中ErrorPage(错误页面)的使用--【ErrorPage组件】
SpringBoot系列文章目录 SpringBoot知识范围-学习步骤–【思维导图知识范围】 文章目录 SpringBoot系列文章目录本系列校训 SpringBoot技术很多很多环境及工具:必要的知识深层一些的知识 上效果图在Spring Boot里使用ErrorPage还要注意的是 配套资源作业ÿ…...

【Android】APP网络优化学习笔记
网络优化原因 进行网络优化对于移动应用程序而言非常重要,原因如下: 用户体验: 网络连接是移动应用程序的核心功能之一。通过进行网络优化,可以提高应用的加载速度和响应速度,减少用户等待时间,提供更流…...
简单的知识图谱可视化+绘制nx.Graph()时报错TypeError: ‘_AxesStack‘ object is not callable
绘制nx.Graph时报错TypeError: _AxesStack object is not callable 写在最前面知识图谱可视化预期报错可能的原因 原代码原因确认解决后的代码解决! 写在最前面 实现一个简单的知识图谱的可视化功能。 使用了NetworkX库来构建知识图谱,并使用matplotlib…...
)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据)
【Matlab】基于粒子群优化算法优化BP神经网络的时间序列预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码5.1 fun.m5.2 main.m6.完整代码6.1 fun.m6.2 main.m7.运行结果1.模型原理 基于粒子群优化算法(Particle Swarm Optimization, PSO)优…...
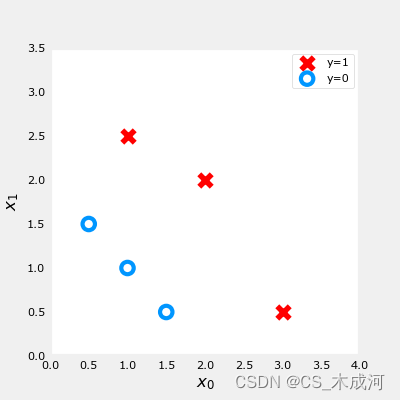
【机器学习】Cost Function for Logistic Regression
Cost Function for Logistic Regression 1. 平方差能否用于逻辑回归?2. 逻辑损失函数loss3. 损失函数cost附录 导入所需的库 import numpy as np %matplotlib widget import matplotlib.pyplot as plt from plt_logistic_loss import plt_logistic_cost, plt_two_…...

【EI/SCOPUS会议征稿】2023年第四届新能源与电气科技国际学术研讨会 (ISNEET 2023)
作为全球科技创新大趋势的引领者,中国一直在为科技创新创造越来越开放的环境,提高学术合作的深度和广度,构建惠及全民的创新共同体。这些努力为全球化和创建共享未来的共同体做出了新的贡献。 为交流近年来国内外在新能源和电气技术领域的最新…...
【计算机网络】10、ethtool
文章目录 一、ethtool1.1 常见操作1.1.1 展示设备属性1.1.2 改变网卡属性1.1.2.1 Auto-negotiation1.1.2.2 Speed 1.1.3 展示网卡驱动设置1.1.4 只展示 Auto-negotiation, RX and TX1.1.5 展示统计1.1.7 排除网络故障1.1.8 通过网口的 LED 区分网卡1.1.9 持久化配置(…...

什么是前端工程化?
工程化介绍 什么是前端工程化? 前端工程化是一种思想,而不是某种技术。主要目的是为了提高效率和降低成本,也就是说在开发的过程中可以提高开发效率,减少不必要的重复性工作等。 tip 现实生活举例 建房子谁不会呢?请…...

【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程
【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程 文章目录 【深度学习】【三维重建】windows11环境配置tiny-cuda-nn详细教程前言确定版本对应关系源码编译安装tiny-cuda-nn总结 前言 本人windows11下使用【Instant Neural Surface Reconstruction】算法时需要…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
