leetcode 912.排序数组
⭐️ 题目描述
🌟 leetcode链接:排序数组
思路: 此题如果使用冒泡插入选择这些时间复杂度 O ( N 2 ) O(N^2) O(N2) 的算法会超时,使用快排 + 优化也过不去,因为里面有一个测试用例全是 2 即使加了三数取中也会是 O ( N 2 ) O(N^2) O(N2) ,以下实现主要使用归并排序。如果需要其他排序的可以看我往期的排序详解✨ 七大经典比较排序算法
代码:
void mergeSort (int * nums , int begin , int end , int* temp) {// 区间不存在if (begin >= end) {return;}int midIndex = (begin + end) >> 1;mergeSort(nums , begin , midIndex , temp);mergeSort(nums , midIndex + 1 , end , temp);int leftBegin = begin;int leftEnd = midIndex;int rightBegin = midIndex + 1;int rightEnd = end;int i = begin;while (leftBegin <= leftEnd && rightBegin <= rightEnd) {if (nums[leftBegin] < nums[rightBegin]) {temp[i++] = nums[leftBegin++];} else {temp[i++] = nums[rightBegin++];}}while (leftBegin <= leftEnd) {temp[i++] = nums[leftBegin++];}while (rightBegin <= rightEnd) {temp[i++] = nums[rightBegin++];}// 拷贝memcpy(nums + begin , temp + begin , sizeof(int) * (end - begin + 1));
}int* sortArray(int* nums, int numsSize, int* returnSize){*returnSize = numsSize;// 直接归并排序秒杀int * temp = (int*)malloc(sizeof(int) * numsSize);mergeSort(nums , 0 , numsSize - 1 , temp);free(temp);return nums;
}
相关文章:

leetcode 912.排序数组
⭐️ 题目描述 🌟 leetcode链接:排序数组 思路: 此题如果使用冒泡插入选择这些时间复杂度 O ( N 2 ) O(N^2) O(N2) 的算法会超时,使用快排 优化也过不去,因为里面有一个测试用例全是 2 即使加了三数取中也会是 O (…...

利用MMPreTrain微调图像分类模型
前言 MMPreTrain是一款基于PyTorch的开源深度学习预工具箱,是OpenMMLab项目的成员之一MMPreTrain的主要特性有: 支持多元化的主干网络与预训练模型支持多种训练策略(有监督学习,无监督学习,多模态学习等)提…...

express学习笔记3 - 三大件
便于统一管理router,创建 router 文件夹,创建 router/index.js: const express require(express)// 注册路由 const router express.Router() router.get(/,function(req,res){res.send(让我们开始express之旅) }) /*** 集中处理404请求的…...
Java课题笔记~Maven基础
2、Maven 基础 2.1 Maven安装与配置 下载安装 配置:修改安装目录/conf/settings.xml 本地仓库:存放的是下载的jar包 中央仓库:要从哪个网站去下载jar包 - 阿里云的仓库 2.2 创建Maven项目...

三步问题(力扣)n种解法 JAVA
目录 题目:1、dfs:2、dfs 备忘录(剪枝):(1)神器 HashMap 备忘录:(2)数组 memo 备忘录: 3、动态规划:4、利用 static 的储存功能:&…...

flask---》登录认证装饰器/配置文件/路由系统
登录认证装饰器 # 0 装饰器的本质原理-# 类装饰器:1 装饰类的装饰器 2 类作为装饰器 # 1 装饰器使用位置,顺序 # 3 flask路由下加装饰器,一定要加endpoint-如果不指定endpoint,反向解析的名字都是函数名,不加装饰器…...
)
Jvm实际运行情况-JVM(十七)
上篇文章说jmap和jstat的命令,如何查看youngGc和FullGc耗时和次数。 Jmap-JVM(十六) Jvm实际运行情况 背景: 机器配置:2核4G JVM内存大小:2G 系统运行天数:7天 期间发生FULL GC次数和耗时…...
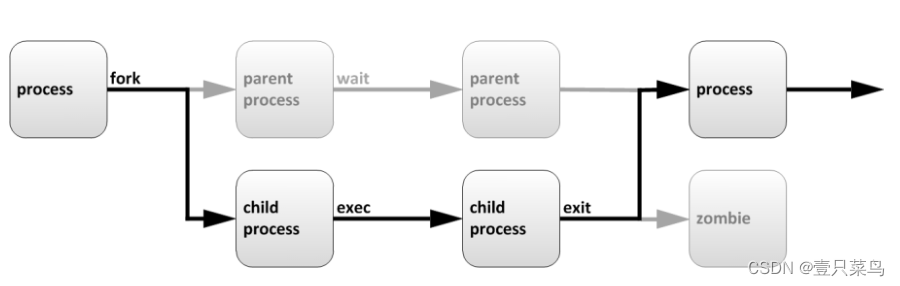
【BASH】回顾与知识点梳理(二)
【BASH】回顾与知识点梳理 二 二. Shell 的变量功能2.1 什么是变量?2.2 变量的取用与设定: echo, 变量设定规则: set/unset2.3 环境变量的功能用 set 观察所有变量 (含环境变量与自定义变量)export: 自定义变量转成环境变量那如何将环境变量转成自定义变…...

【分布式训练】Accelerate 多卡训练,单卡评测,进程卡住的解决办法
最近想把之前的一个模型的改成多卡训练的。我并不懂DDP,DP。一开始打算使用Transformers的Trainer,但是配置的过程踩了很多坑也没有弄成功。【我是自己写的评测方法,但是我找不到能让触发Trainer去用我的方法评测的路劲】,后来偶然…...

时间复杂度为O(nlogn)的两种排序算法
1.归并排序 归并排序的核心思想:如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。 归并排序使用的就是分治思想。分治&#x…...

java调用onnx模型,支持yolov5和yolov7
不点star不给解答问题 可直接运行主文件:ObjectDetection_1_25200_n.java 或者 ObjectDetection_n_7.java 都可以直接运行两个可以运行的主文件是为了支持不用网络结构的模型,即使是onnx模型,输出的结果参数也不一样,支持以下两种…...
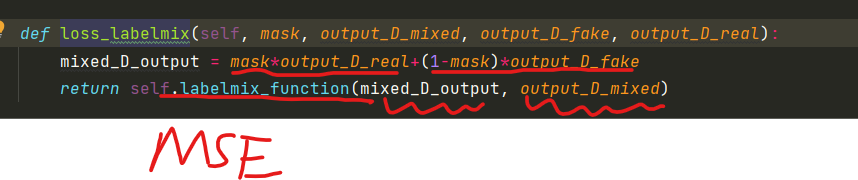
DP-GAN损失
在前面我们看了生成器和判别器的组成。 生成器损失公式: 首先将fake image 和真实的 image输入到判别器中: 接着看第一个损失:参数分别为fake image经过判别器的输出mask,和真实的label进行损失计算。对应于: 其中l…...

自监督去噪:Noise2Void原理和调用(Tensorflow)
文章原文: https://arxiv.org/abs/1811.10980 N2V源代码: https://github.com/juglab/n2v 参考博客: https://zhuanlan.zhihu.com/p/445840211https://zhuanlan.zhihu.com/p/133961768https://zhuanlan.zhihu.com/p/563746026 文章目录 1. 方法原理1.1 Noise2Noise回…...
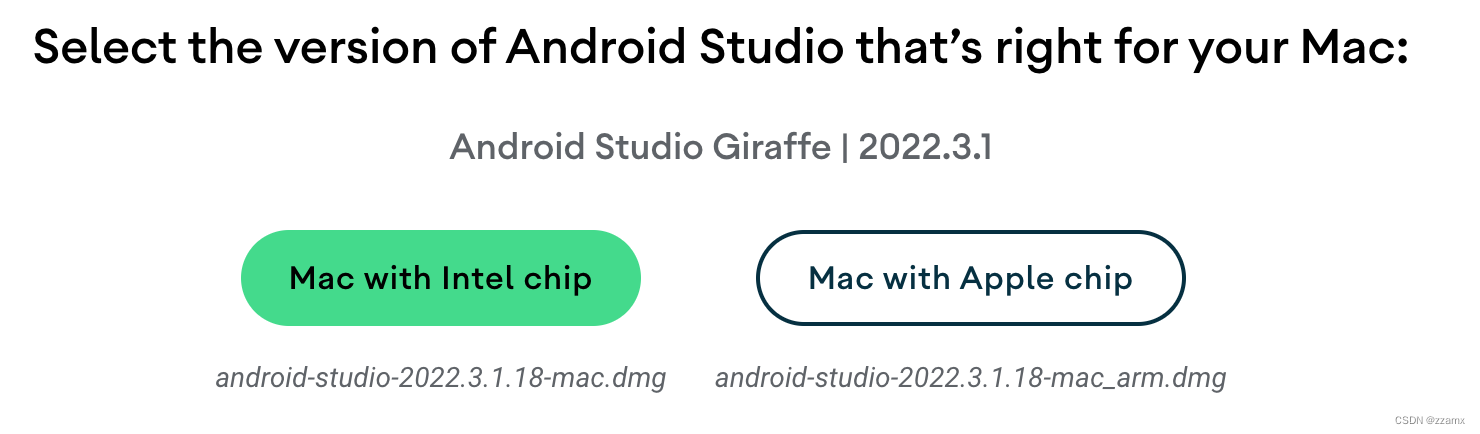
Mac 安装配置adb命令环境(详细步骤)
一、注意:前提要安装java环境。 因为android sdk里边开发的一些包都是依赖java语言的,所以,首先要确保已经配置了java环境。 二、在Mac下配置android adb命令环境,配置方式如下: 1、下载并安装IDE (andr…...
 GDALRasterBand篇 代码示例 翻译 自学)
GDAL C++ API 学习之路 (2) GDALRasterBand篇 代码示例 翻译 自学
GDALRasterBand Class <gdal_priv.h> GDALRasterBand是GDAL中用于表示栅格数据集中一个波段的类。栅格数据集通常由多个波段组成,每个波段包含了特定的数据信息,例如高程、红、绿、蓝色等, 用于表示影像的不同特征。提供了许…...

springboot对静态资源的支持
1、spring boot默认静态路径支持 Spring Boot 默认将 / 所有访问映射到以下目录:** classpath:/static classpath:/public classpath:/resources classpath:/META-INF/resources也就是说什么也不用配置,通过浏览器可以直接访问这几个目录下的文件。 1…...

WPF实战学习笔记27-全局通知
新建消息事件 添加文件:Mytodo.Common.Events.MessageModel.cs using Prism.Events; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Diagnostics;namespace Mytod…...

openSUSE安装虚拟化 qemu kvm
1) 第一种:图形界面yast安装虚拟化 左下角开始菜单搜索yast 点一下就能安装,是不是很简单呢 2)第二种: 命令行安装 网上关于openSUSE安装qemu kvm的教程比较少,可以搜索centos7 安装qemu kvm的教程,然后…...
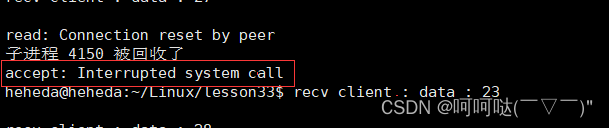
基于linux下的高并发服务器开发(第四章)- 多进程实现并发服务器(回射服务器)
1. socket // 套接字通信分两部分: - 服务器端:被动接受连接,一般不会主动发起连接 - 客户端:主动向服务器发起连接 2.字节序转换函数 当格式化的数据在两台使用不同字节序的主机之间直接传递时,接收端必然错误…...

【程序分析】符号执行
符号执行入门 参考:https://zhuanlan.zhihu.com/p/26927127 给定一个结果,求解对应的程序输入。 经典符号执行与动态符号执行 参考:https://p1kk.github.io/2021/04/04/others/%E7%AC%A6%E5%8F%B7%E6%89%A7%E8%A1%8C&%E6%B1%A1%E7%82…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
