二、搜索与图论6:Dijkstra 模板题+算法模板(Dijkstra求最短路 I, Dijkstra求最短路 II,1003 Emergency)
文章目录
- 算法模板
- Dijkstra题目代码模板
- 朴素dijkstra算法
- 堆优化版dijkstra
- 树与图的存储
- (1) 邻接矩阵:
- (2) 邻接表:
- 关于e[],ne[],h[]的理解
- 关于堆的原理与操作
- 模板题
- Dijkstra求最短路 I
- 原题链接
- 题目
- 思路
- 题解
- Dijkstra求最短路 II
- 原题链接
- 题目
- 思路
- 题解
- 1003 Emergency
- 原题链接
- 题目
- 思路
- 题解
算法模板
Dijkstra题目代码模板
朴素dijkstra算法
对应模板题:Dijkstra求最短路 I
时间复杂是 O(n^2+m):n 表示点数,m 表示边数


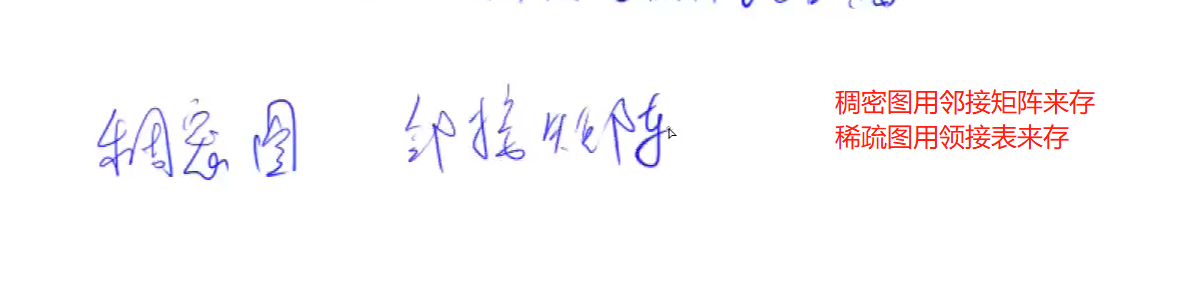
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i ++ ){int t = -1; // 在还未确定最短路的点中,寻找距离最小的点for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;// 用t更新其他点的距离for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
堆优化版dijkstra
对应模板题:Dijkstra求最短路 II
时间复杂度 O(mlogn):n 表示点数,m 表示边数



typedef pair<int, int> PII;int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1}); // first存储距离,second存储节点编号while (heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;if (st[ver]) continue;st[ver] = true;for (int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}
树与图的存储
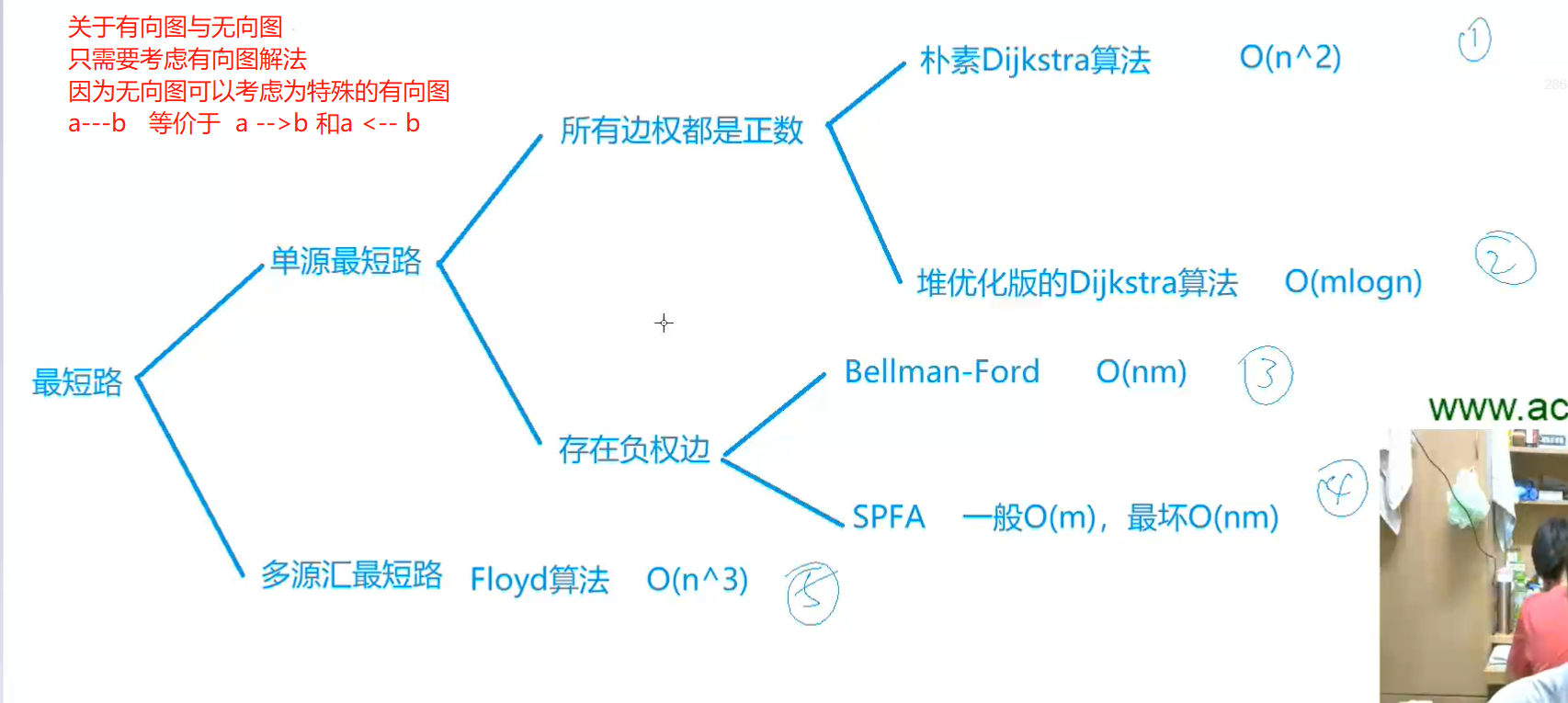
树是一种特殊的图,与图的存储方式相同。
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
(1) 邻接矩阵:
g[a][b] 存储边a->b
(2) 邻接表:
https://www.acwing.com/video/21/
(1:20:00左右)
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
int h[N], e[N], ne[N], idx;// 添加一条边a->b
void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}int main(){...// 初始化idx = 0;memset(h, -1, sizeof h);...
}
有权重时模板:
int h[N],w[N],e[N],ne[N],idx; void add(int a,int b,int c){e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
关于e[],ne[],h[]的理解
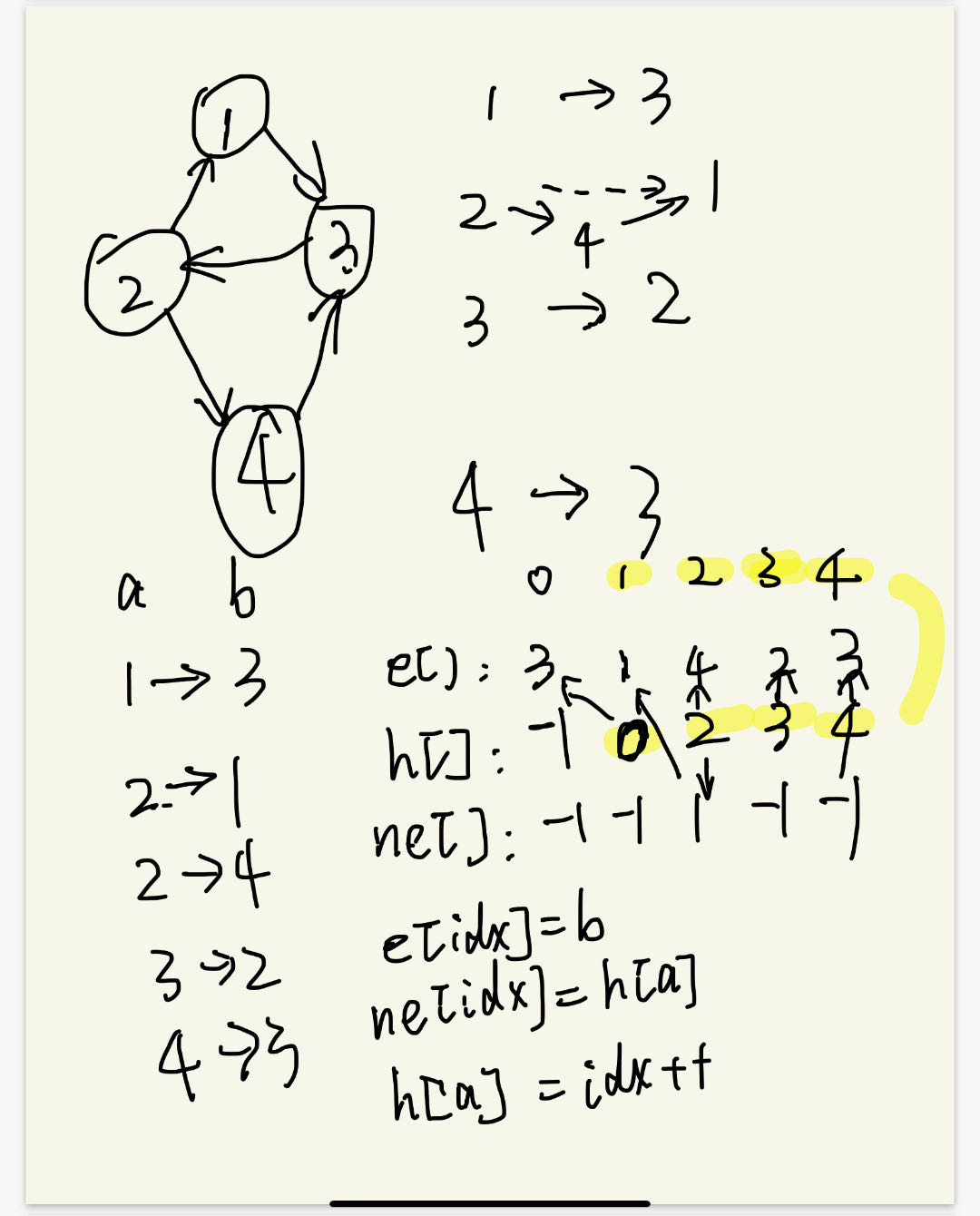
h[N] : 表示 第 i 个节点的 第一条边的 idx
ne[M] : 表示 与 第 idx 条边 同起点 的 下一条边 的 idx
e[M] : 表示 第idx 条边的 终点
N : 节点数量
M:边的数量
i : 节点的下标索引
idx : 边的下标索引
变量初始化定义:
int h[N], e[M], ne[M], idx;
当我们加入一条边的时候:
void add(int a,int b){e[idx] = b; // 记录 加入的边 的终点节点ne[idx] = h[a]; // h[a] 表示 节点 a 为起点的第一条边的下标,ne[idx] = h[a] 表示把 h[a] 这条边接在了 idx 这条边的后面,其实也就是把 a 节点的整条链表 接在了 idx 这条边 后面;目的就是为了下一步 把 idx 这条边 当成 a 节点的单链表的 第一条边,完成把最新的一条边插入到 链表头的操作;h[a] = idx++; // a节点开头的第一条边置为当前边,idx移动到下一条边
}
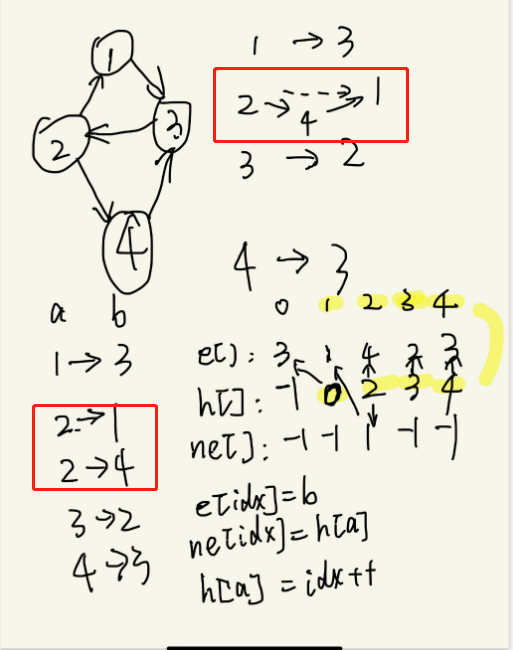
要注意的是邻接表插入新节点时使用的是“头插”,如图中节点2:当插入2 1时此时为2—>1, 而后插入2 4后,此时为 2—> 4 —> 1.
关于堆的原理与操作
二、数据结构10:堆 模板题+算法模板(堆排序,模拟堆)
模板题
Dijkstra求最短路 I
原题链接
https://www.acwing.com/problem/content/851/
题目
给定一个 n
个点 m
条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1
号点到 n
号点的最短距离,如果无法从 1
号点走到 n
号点,则输出 −1
。
输入格式
第一行包含整数 n
和 m
。
接下来 m
行每行包含三个整数 x,y,z
,表示存在一条从点 x
到点 y
的有向边,边长为 z
。
输出格式
输出一个整数,表示 1
号点到 n
号点的最短距离。
如果路径不存在,则输出 −1
。
数据范围
1≤n≤500
,
1≤m≤105
,
图中涉及边长均不超过10000。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路


题解
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
const int M = 1e5 + 10;
int dist[N]; // 存各点与1号点的最短距离
bool st[N]; // 存各点是否已被 处理为最短距离点 判断 (当前已确定最短距离的点)
int g[N][N];
int n,m,t;int dijkstra(){memset(dist,0x3f,sizeof dist);dist[1] = 0;for(int i = 0;i<n;i++){t = -1; // t: 不在 当前已确定最短距离的点 中的距离最短的点 初始化为-1 for(int j = 1;j<=n;j++){if(!st[j] && (t == -1 || dist[t] > dist[j])){t = j;}}st[t] = true;for(int j=1;j<=n;j++){dist[j] = min(dist[j],dist[t] + g[t][j]); //用(1到t+t到j)的长度与(1到j)的长度进行对比更新 }}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
int main(){cin>>n>>m;memset(g,0x3f,sizeof g);for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;g[x][y] = min(g[x][y],z);} int res = dijkstra();printf("%d",res);return 0;}
Dijkstra求最短路 II
原题链接
https://www.acwing.com/problem/content/852/
题目
给定一个 n
个点 m
条边的有向图,图中可能存在重边和自环,所有边权均为非负值。
请你求出 1
号点到 n
号点的最短距离,如果无法从 1
号点走到 n
号点,则输出 −1
。
输入格式
第一行包含整数 n
和 m
。
接下来 m
行每行包含三个整数 x,y,z
,表示存在一条从点 x
到点 y
的有向边,边长为 z
。
输出格式
输出一个整数,表示 1
号点到 n
号点的最短距离。
如果路径不存在,则输出 −1
。
数据范围
1≤n,m≤1.5×105
,
图中涉及边长均不小于 0
,且不超过 10000
。
数据保证:如果最短路存在,则最短路的长度不超过 109
。
输入样例:
3 3
1 2 2
2 3 1
1 3 4
输出样例:
3
思路
使用堆优化,选择用stl中的priority_queue进行操作
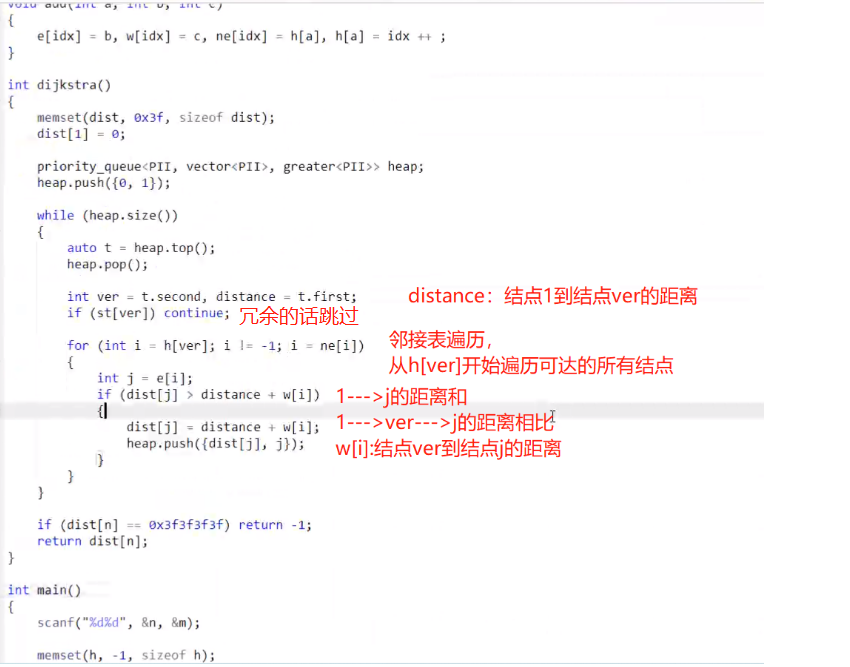
关于st[N]数组 处理冗余部分
https://www.acwing.com/solution/content/167860/
题解
#include <iostream>
#include <algorithm>
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
const int M = 2e5 + 10;
typedef pair<int,int> PII;
int dist[N]; // 存各点与1号点的最短距离
bool st[N]; // 存各点是否已被 处理为最短距离点 判断 (当前已确定最短距离的点)
//int g[N][N];
//堆优化中,由于为稀疏图,因此使用邻接表进行存储
int h[N],w[N],e[N],ne[N],idx; int n,m,t;//邻接表插入处理
void add(int a,int b,int c){e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}int dijkstra(){memset(dist,0x3f,sizeof dist);dist[1] = 0;// 堆优化版dijkstrapriority_queue<PII,vector<PII>,greater<PII>> heap;heap.push({0,1}); // {距离,编号}编号为1的点距离为0,表示1到1的距离为0 while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first; // distance :结点1到结点ver的距离if(st[ver]) continue; // 冗余的话跳过st[ver] = true;for(int i=h[ver]; i!=-1; i=ne[i]){ // 邻接表遍历,从h[ver]开始遍历可达的所有结点int j = e[i];// w[i]:结点ver到结点j的距离if(dist[j]>distance + w[i]){ // 1--->i的距离 和 1--->ver--->i的距离相比dist[j] = distance + w[i]; heap.push({dist[j],j});}} }if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
int main(){cin>>n>>m;
// memset(g,0x3f,sizeof g);memset(h,-1,sizeof h);;for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;add(x,y,z);} int res = dijkstra();printf("%d",res);return 0;}
1003 Emergency
原题链接
原题链接
题目
题目大意:n个城市m条路,每个城市有救援小组,所有的边的边权已知。给定起点和终点,求从起点到终点的最短路径条数以及最短路径上的救援小组数目之和。如果有多条就输出点权(城市救援小组数目)最大的那个
思路
用一遍Dijkstra算法,救援小组个数相当于点权,用Dijkstra求边权最小的最短路径的条数,以及这些最短路径中点权最大的值
dis[i]表示从出发点到i结点最短路径的路径长度,
num[i]表示从出发点到i结点最短路径的条数,
w[i]表示从出发点到i点救援队的数目之和
当判定dis[u] + e[u][v] < dis[v]的时候,
不仅仅要更新dis[v],还要更新num[v] = num[u], w[v] = weight[v] + w[u];
如果dis[u] + e[u][v] == dis[v],还要更新num[v] += num[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u];
题解
基于上述朴素版dijkstra进行改进,
#include <bits/stdc++.h>
using namespace std;
//题目大意:n个城市m条路,每个城市有救援小组,所有的边的边权已知。给定起点和终点,求从起点到终点的最短路径条数以及最短路径上的救援小组数目之和。如果有多条就输出点权(城市救援小组数目)最大的那个~
//
//分析:用一遍Dijkstra算法~救援小组个数相当于点权,用Dijkstra求边权最小的最短路径的条数,以及这些最短路径中点权最大的值~dis[i]表示从出发点到i结点最短路径的路径长度,num[i]表示从出发点到i结点最短路径的条数,w[i]表示从出发点到i点救援队的数目之和~当判定dis[u] + e[u][v] < dis[v]的时候,不仅仅要更新dis[v],还要更新num[v] = num[u], w[v] = weight[v] + w[u]; 如果dis[u] + e[u][v] == dis[v],还要更新num[v] += num[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u]; const int N = 510;
int g[N][N];
int c1,c2;
int dist[N]; //dist[i]表示从出发点到i结点最短路径的路径长度
int weight[N]; //每个城市救援队数量
int w[N]; //w[i]表示从出发点到i点救援队的数目之和
bool st[N];
int num[N]; //num[i]表示从出发点到i结点最短路径的条数int n,m;void dij(){w[c1] = weight[c1];memset(dist,0x3f,sizeof dist);dist[c1] = 0;num[c1] = 1;int t;for(int i=0;i<n;i++){t = -1;for(int j=0;j<n;j++){if(!st[j] && (t==-1 || dist[t] >dist[j]) ){t = j;}}st[t] = true;for(int j=0;j<n;j++){
// dist[j] = min(dist[j],dist[t] + g[t][j]);if(dist[j]>dist[t]+g[t][j]){ //当判定dis[u] + e[u][v] < dis[v]的时候,不仅仅要更新dis[v],还要更新num[v] = num[u], w[v] = weight[v] + w[u]; dist[j] = dist[t]+g[t][j];num[j] = num[t];w[j] = w[t] + weight[j];
// cout<<t<<" "<<w[t]<<endl;
// w[j]+=weight[t];}else if(dist[j]==dist[t]+g[t][j]){ //如果dis[u] + e[u][v] == dis[v],还要更新num[v] += num[u],而且判断一下是否权重w[v]更小,如果更小了就更新w[v] = weight[v] + w[u]; num[j] = num[t]+num[j];if(w[t]+weight[j] > w[j]){w[j] = w[t] + weight[j];}} }}// return w[c2];
}
int main(){cin>>n>>m>>c1>>c2;for(int i=0;i<n;i++){int t;cin>>t;weight[i] = t;}memset(g,0x3f,sizeof g); // 赋值无穷大 for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;g[x][y] = g[y][x] = z; // 无向图!所以存双向信息 }dij();cout<<num[c2]<<" "<<w[c2];
}
参考链接:1003. Emergency (25)-PAT甲级真题(Dijkstra算法)
相关文章:

二、搜索与图论6:Dijkstra 模板题+算法模板(Dijkstra求最短路 I, Dijkstra求最短路 II,1003 Emergency)
文章目录 算法模板Dijkstra题目代码模板朴素dijkstra算法堆优化版dijkstra 树与图的存储(1) 邻接矩阵:(2) 邻接表:关于e[],ne[],h[]的理解 关于堆的原理与操作 模板题Dijkstra求最短路 I原题链接题目思路题解 Dijkstra求最短路 II原题链接题目思路题解 1…...
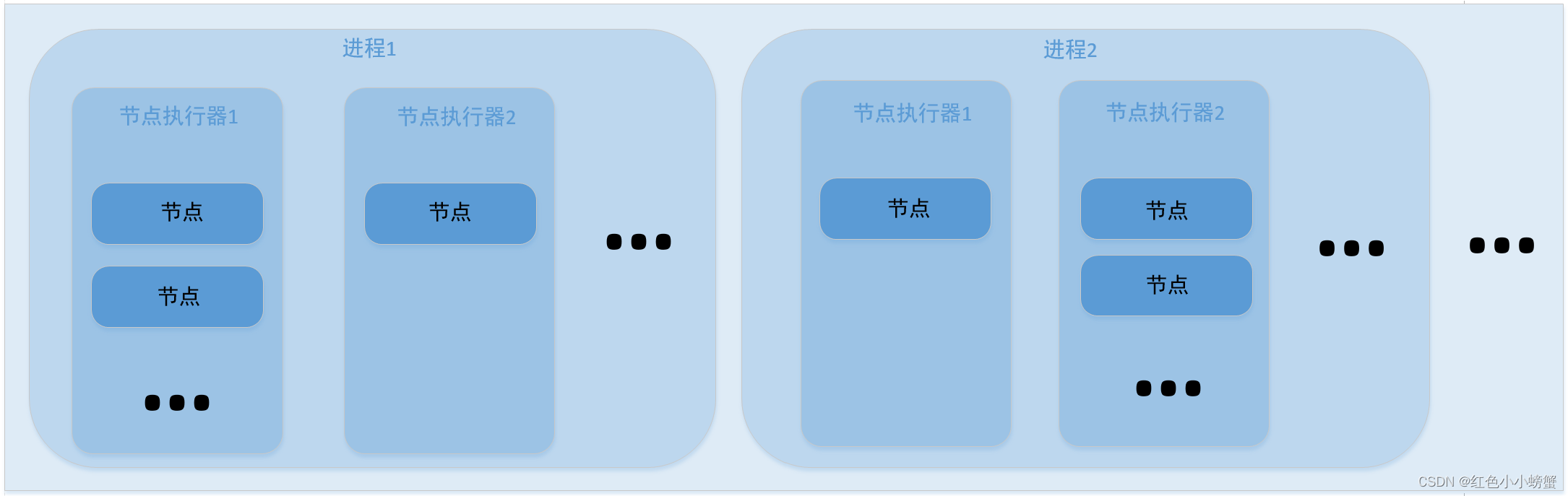
ROS2学习(四)进程,线程与节点的关系
节点与节点执行器 节点,英文是node,在ROS2中,节点是一个抽象的实体,它可以代表某种或某类特定功能的抽象集合体,它可以存在于进程中,也可以存在于线程中。所有ROS2的基础功能最基础的载体是节点,所有的通信…...

【物联网】DMA传输原理与实现详解(超详细)
DMA(Direct Memory Access,直接内存访问)是一种计算机数据传输方式,允许外围设备直接访问系统内存,而无需CPU的干预。 文章目录 Part 1: DMA的工作原理配置阶段:数据传输阶段: Part 2: DMA数据…...
Java类集框架(二)
目录 1.Map(常用子类 HashMap,LinkedHashMap,HashTable,TreeMap) 2.Map的输出(Map.Entry,iterator,foreach) 3.数据结构 - 栈(Stack) 4.数据结构 - 队列(Q…...

爬虫008_流程控制语句_if_if else_elif_for---python工作笔记026
然后我们再来看一下这里的,判断,可以看到 再看一个判断,这里的布尔类型 第二行有4个空格,python的格式 注意这里,输入的age是字符串,需要转一下才行 int可以写到int(intput("阿斯顿法师打发地方")) 这样也可以...

【随笔】五周年创作纪念日
今天收到了 CSDN 的创作五周年提示,正好前几天(7.31)我也成功申请了 CSDN 博客专家,趁这个机会分享一下这几年写博客的感受吧 机缘 关注我比较久的读者应该知道我是从学传统工科半路出家搞计算机的,这里的经历还是比…...
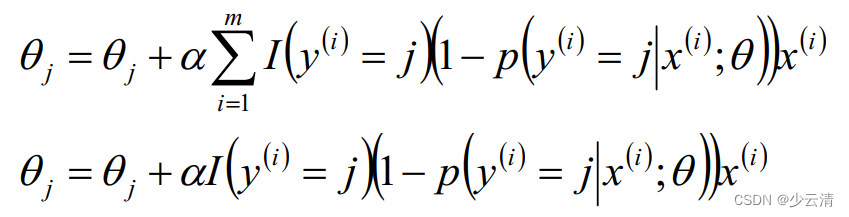
7_分类算法—逻辑回归
文章目录 逻辑回归:1 Logistic回归(二分类问题)1.1 sigmoid函数1.2 Logistic回归及似然函数(求解)1.3 θ参数求解1.4 Logistic回归损失函数1.5 LogisticRegression总结 2 Softmax回归(多分类问题࿰…...
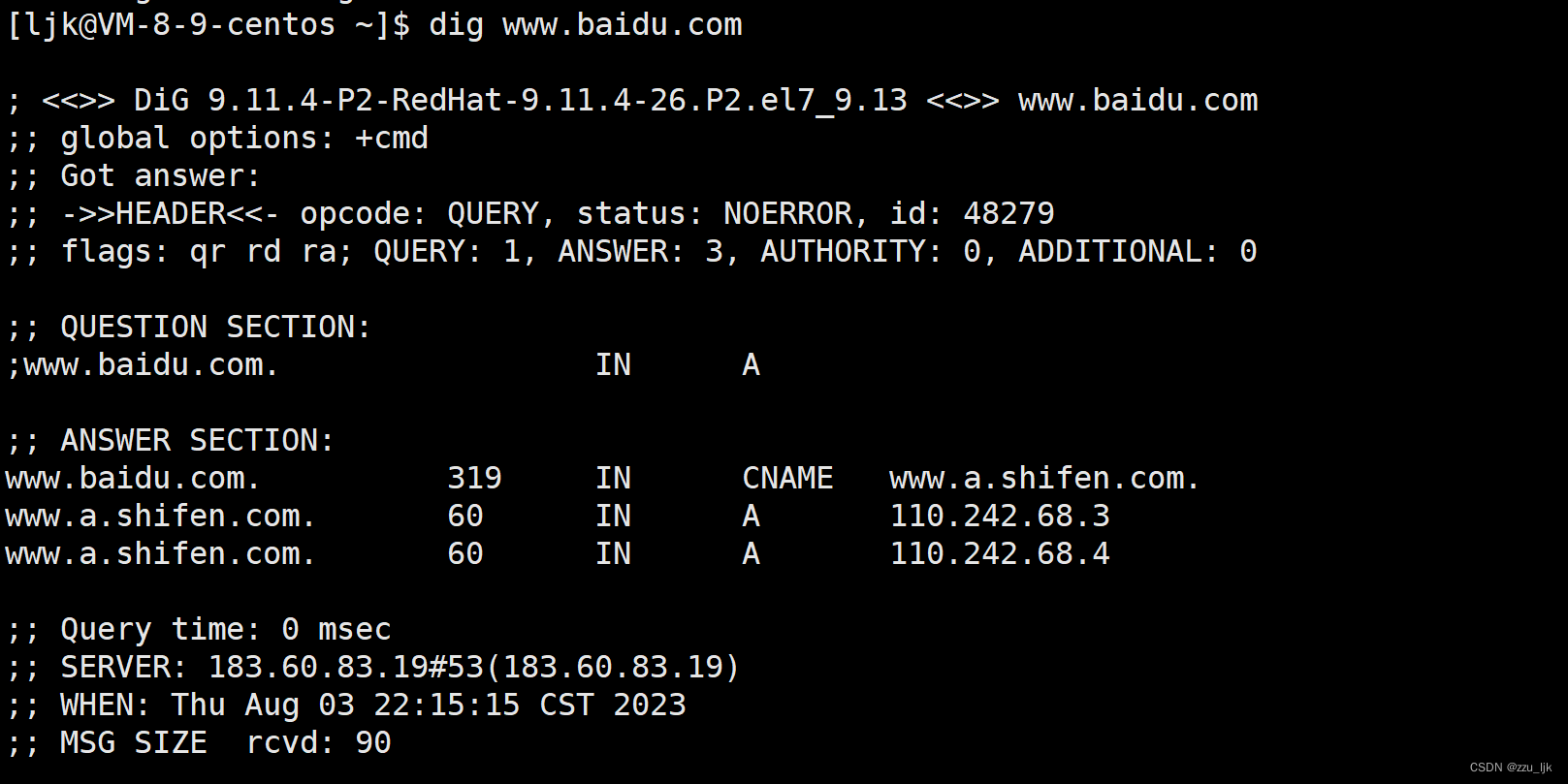
【计算机网络】应用层协议 -- DNS协议
文章目录 1. DNS背景2. 域名简介3. 域名解析过程4. 使用dig查看DNS过程 1. DNS背景 DNS(Domain Name System,域名系统)协议,是一个用来将域名转化为IP地址的应用层协议。 TCP/IP当中通过IP地址和端口号的方式,来确定…...

ES6 - 数组新增的一些常用方法
文章目录 1,Array.from()2,Array.of()3,find(),findIndex(),findLast()和findLastIndex()4,Array.fill()5,keys(),values() 和 entries()6,Array.includes()7,…...
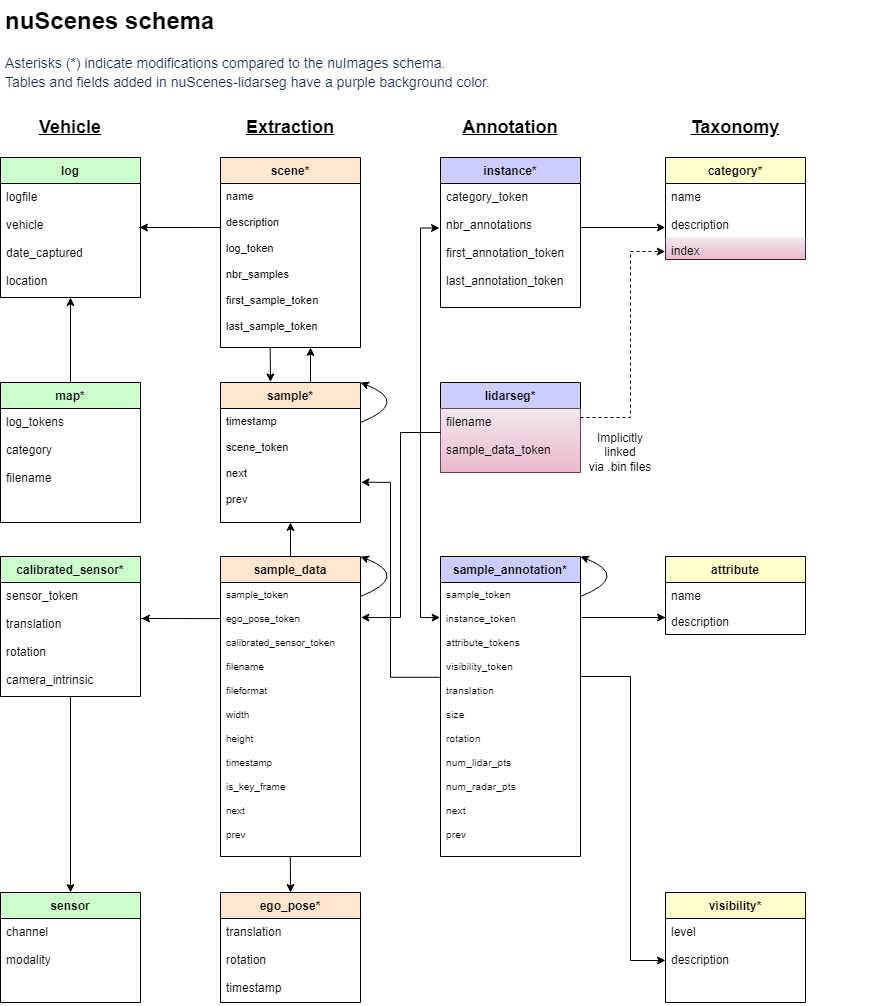
【BEV感知】3-BEV开源数据集
3-BEV开源数据集 1 KITTI1.1 KITTI数据怎么采集?1.2 KITTI数据规模有多大?1.3 KITTI标注了哪些目标?1.4 转换矩阵1.5 标签文件 2 nuScenes2.1 nuScenes Vs KITTI2.2 标注文件 1 KITTI KITTI 1.1 KITTI数据怎么采集? 通过车载相机、激光雷达等传感器采集。 只提供了相机正…...
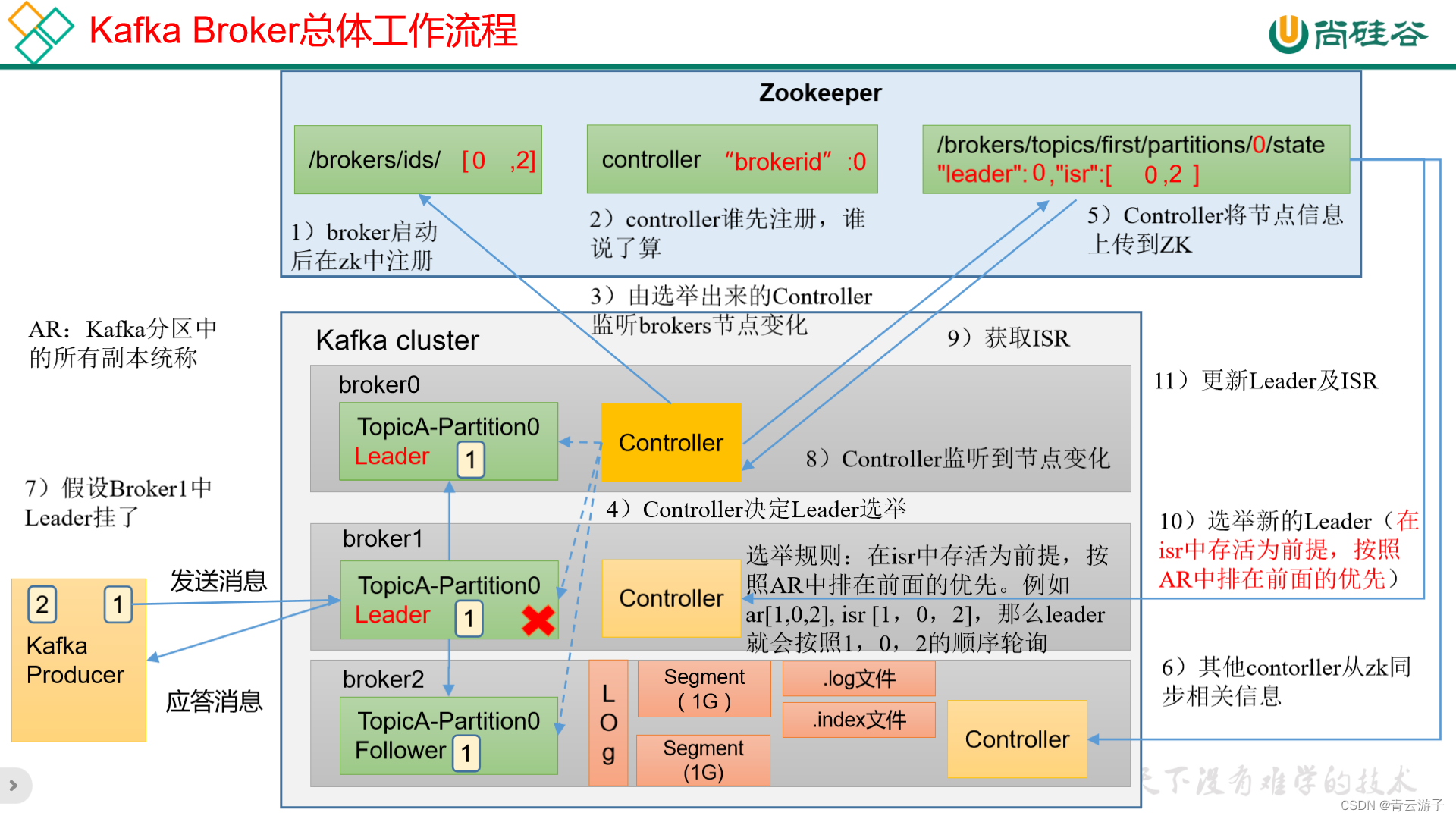
Kafka-Broker工作流程
kafka集群在启动时,会将每个broker节点注册到zookeeper中,每个broker节点都有一个controller,哪个controller先在zookeeper中注册,哪个controller就负责监听brokers节点变化,当有分区的leader挂掉时,contro…...

第八篇-Tesla P40+ChatGLM2+LoRA
部署环境 系统:CentOS-7CPU: 14C28T显卡:Tesla P40 24G驱动: 515CUDA: 11.7cuDNN: 8.9.2.26目的 验证P40部署可行性,只做验证学习lora方式微调创建环境 conda create --name glm-tuning python3.10 conda activate glm-tuning克隆项目 git clone http…...

调用feign返回错误的数据
bug描述: 在一个请求方法中会调用到feign去获取其他的数据。 List<Demo> list aaaFeignApi.getData(personSelectGetParam);在调用的时候,打断点到feign的地方,数据是存在的,并且有15条。但是返回到上面代码的时候数据就…...
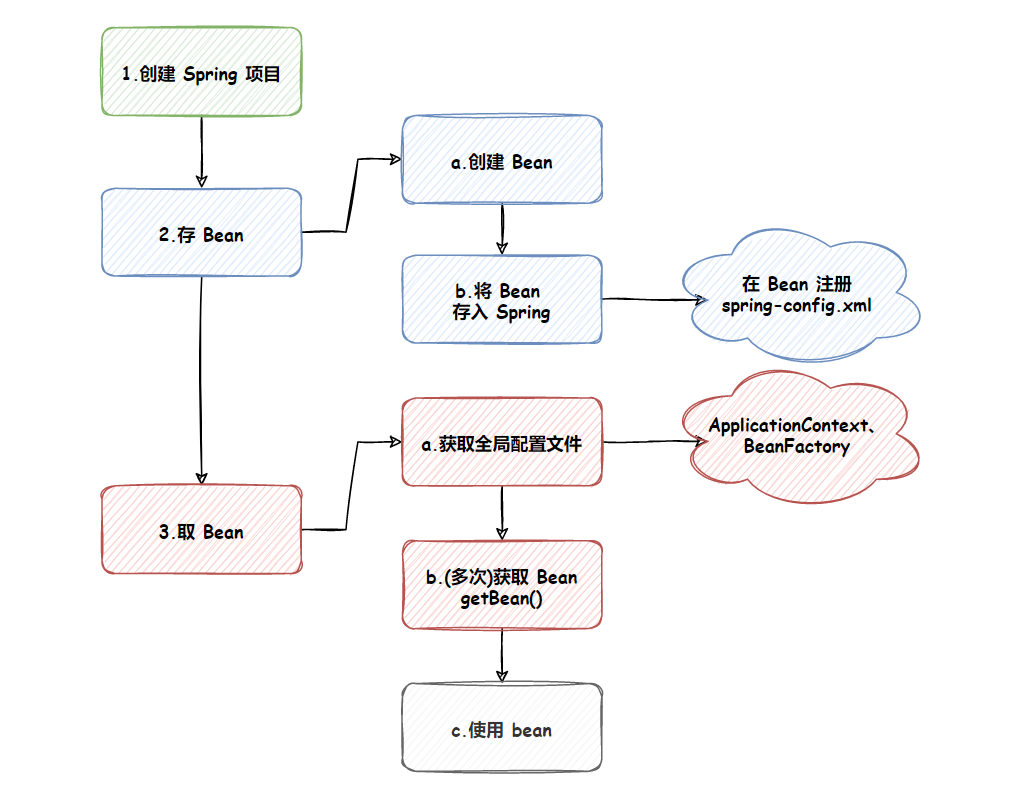
【Spring】(二)从零开始的 Spring 项目搭建与使用
文章目录 前言一、Spring 项目的创建1.1 创建 Maven 项目1.2 添加 Spring 框架支持1.3 添加启动类 二、储存 Bean 对象2.1 创建 Bean2.1 将 Bean 注册到 Spring 容器 三、获取并使用 Bean 对象3.1 获取Spring 上下文3.2 ApplicationContext 和 BeanFactory 的区别3.3 获取指定的…...

redis五种数据类型介绍
、string(字符串) 它师最基本的类型,可以理解为Memcached一模一样的类型,一个key对应一个value。 注意:一个键最大能存储 512MB。 特性:可以包含任何数据,比如jpg图片或者序列化的对象,一个键最大能存储512…...
【JavaEE】Spring Boot - 项目的创建和使用
【JavaEE】Spring Boot 开发要点总结(1) 文章目录 【JavaEE】Spring Boot 开发要点总结(1)1. Spring Boot 的优点2. Spring Boot 项目创建2.1 下载安装插件2.2 创建项目过程2.3 加载项目2.4 启动项目2.5 删除一些没用的文件 3. Sp…...

Git reset、revert用法
reset reset是删除之前的提交记录,所有的提交点都会被清除,我们看下执行前后的git log区别 D:\workspace\android>git log commit 87c1277a57544c53c603b04110e3dde100da8f57 (HEAD -> develop_main) Author: test <test.com> Date: Wed…...

Redis-1
Redis 理论部分 redis 速度快的原因 1、纯内存操作 2、单线程操作,避免了频繁的上下文切换和资源争用问题,多线程需要占用更多的 CPU 资源 3、采用了非阻塞 I/O 多路复用机制 4、提供了非常高效的数据结构,例如双向链表、压缩页表和跳跃…...

【Linux】Linux服务器连接百度网盘:实现上传下载
【Linux】Linux服务器连接百度网盘:实现上传下载 文章目录 【Linux】Linux服务器连接百度网盘:实现上传下载1. 前言2. 具体过程2.1 pip 安装所需包2.2 认证(第一次连接需要认证)2.3 下载所需文件或者目录2.4 其他指令使用2.5 注意…...
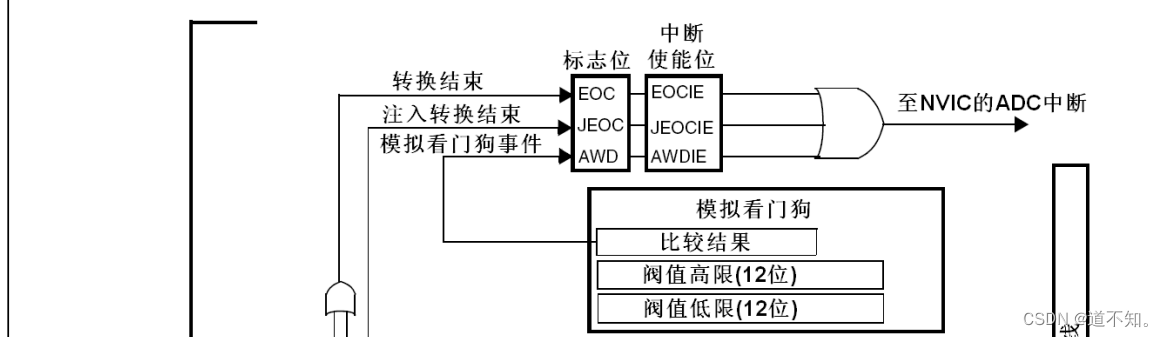
ADC模拟看门狗
如果被ADC转换的模拟电压低于低阀值或高于高阀值,AWD模拟看门狗状态位被设置。阀值位 于ADC_HTR和ADC_LTR寄存器的最低12个有效位中。通过设置ADC_CR1寄存器的AWDIE位 以允许产生相应中断。通过以下函数可以进行配置 void ADC_AnalogWatchdogCmd(ADC_TypeDef* ADCx…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
