缓存友好在实际编程中的重要性
引入
当CPU执行程序时,需要频繁地访问主存储器(RAM)中的数据和指令。然而,主存储器的访问速度相对较慢,与CPU的运算速度相比存在显著差异,每次都从主存中读取数据都会导致相对较长的等待时间,从而降低计算机的整体性能。为了减弱这种速度差异带来的影响,计算机系统引入了高速缓存(cache)作为中间层,用于存储主存储器中CPU经常访问的数据和指令。
所以,高速缓存应该缓存哪些数据以尽可能提高缓存命中率呢?这就涉及到了局部性原理的作用。
局部性原理
局部性原理是指程序访问数据和指令的模式往往具有以下两种特点:
- 时间局部性:如果一个存储位置被访问,在不久的将来它很可能再次被访问。这意味着计算机系统很可能会重复地访问同一个数据或指令。
- 空间局部性:如果一个存储位置被访问,附近的存储位置也很可能在不久的将来被访问。这意味着计算机系统在访问数据或指令时,很可能会顺序地访问附近的数据或指令。
基于局部性原理,高速缓存的设计通常采用了缓存行(Cache Line)的概念。缓存行是高速缓存中最小的存储单元,一般大小为几十字节到几百字节。当CPU访问主存储器的数据时,高速缓存将一整个缓存行的数据加载到缓存中,而不仅仅是所需的单个数据。这样,如果CPU在不久的将来需要附近的数据,它们很可能已经在同一缓存行中了,从而避免了频繁地访问主存储器。
当我们谈论算法或数据结构的“缓存友好”性质时,指的是这些算法或数据结构在计算机的缓存系统中表现良好,从而提高程序的性能。缓存友好性是一个重要的性能指标,以下是三个缓存友好性的测试例子,更深刻体会下缓存友好的重要性。
顺序访问数组
顺序访问数组:顺序访问数组中的元素是缓存友好的操作。当程序连续读取数组的元素时,计算机缓存可以将整个连续的数据块加载到缓存中,从而加快访问速度。相比之下,随机访问数组元素可能导致缓存不命中,需要频繁地从内存中读取数据,降低了访问速度。
通过一个很经典的例子来感受下缓存的存在:假设我们有一个二维矩阵,并且要对它进行某种操作,例如求和或者求积。考虑以下两种遍历方式:
- 行优先遍历:按照行优先遍历矩阵,先访问第一行的所有元素,然后是第二行的所有元素,以此类推。
- 列优先遍历:按照列优先遍历矩阵,先访问第一列的所有元素,然后是第二列的所有元素,以此类推。
因为局部性原理,当我们对矩阵进行遍历时,如果采用行优先遍历方式,那么连续的内存块都是同一行的元素,这样的访问方式在缓存中具有较好的局部性,能够更好地利用缓存,从而提高访问效率。相比之下,如果采用列优先遍历方式,由于矩阵中的元素是按列存储的,访问过程会在内存中跳跃,这会导致缓存不命中,降低访问效率。
import java.util.Random;public class CacheFriendlyTest {public static void main(String[] args) {int rows = 10000;int cols = 10000;int[][] matrix = new int[rows][cols];// Fill the matrix with random valuesRandom random = new Random();for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {matrix[i][j] = random.nextInt(100);}}// Row-wise traversallong startTime = System.currentTimeMillis();long sumRowWise = 0;for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {sumRowWise += matrix[i][j];}}long endTime = System.currentTimeMillis();System.out.println("Row-wise traversal time: " + (endTime - startTime) + " ms");// Column-wise traversalstartTime = System.currentTimeMillis();long sumColWise = 0;for (int j = 0; j < cols; j++) {for (int i = 0; i < rows; i++) {sumColWise += matrix[i][j];}}endTime = System.currentTimeMillis();System.out.println("Column-wise traversal time: " + (endTime - startTime) + " ms");System.out.println("Sum Row-Wise: " + sumRowWise);System.out.println("Sum Col-Wise: " + sumColWise);}
}
因此,虽然两种遍历方式在时间复杂度上是相同的(都是 O ( m ∗ n ) O(m * n) O(m∗n),其中 m 和 n 分别是矩阵的行数和列数),但行优先遍历的实际表现往往比列优先遍历要好得多。
Row-wise traversal time: 45 ms
Column-wise traversal time: 761 ms
Sum Row-Wise: 4949822692
Sum Col-Wise: 4949822692
紧凑数据结构
使用“紧凑”的数据结构可以提高缓存友好性。例如,使用数组而不是链表,因为数组的元素在内存中是连续存储的,而链表的节点分散在内存中,访问链表可能导致缓存不命中。
import java.util.ArrayList;
import java.util.Iterator;
import java.util.LinkedList;public class CompactDataStructureTest {public static void main(String[] args) {int dataSize = 1000000; // 数据规模int repeatCount = 1000;// 使用 ArrayList(数组)实现紧凑的数据结构ArrayList<Integer> arrayList = new ArrayList<>();for (int i = 0; i < dataSize; i++) {arrayList.add(i);}// 使用 LinkedList(链表)实现非紧凑的数据结构LinkedList<Integer> linkedList = new LinkedList<>();for (int i = 0; i < dataSize; i++) {linkedList.add(i);}// 测试 ArrayList 遍历性能long startTime = System.currentTimeMillis();for (int i = 0; i < repeatCount; i++) {Iterator<Integer> arrayIterator = arrayList.iterator();while (arrayIterator.hasNext()) {int value = arrayIterator.next();// 在这里可以对 value 进行一些操作,以避免编译器对循环的优化}}long endTime = System.currentTimeMillis();System.out.println("ArrayList traversal time: " + (endTime - startTime) + " ms");// 测试 LinkedList 遍历性能startTime = System.currentTimeMillis();for (int i = 0; i < repeatCount; i++) {Iterator<Integer> linkedListIterator = linkedList.iterator();while (linkedListIterator.hasNext()) {int value = linkedListIterator.next();// 在这里可以对 value 进行一些操作,以避免编译器对循环的优化}}endTime = System.currentTimeMillis();System.out.println("LinkedList traversal time: " + (endTime - startTime) + " ms");}
}
实际差距并不明显,想来 JDK 对 LinkedList 的存储进行了优化。
ArrayList traversal time: 598 ms
LinkedList traversal time: 2585 ms
矩阵乘法
假设我们有两个 n x n 的矩阵 A 和 B,我们想要计算它们的乘积 C。标准的矩阵乘法算法需要 O ( n 3 ) O(n^3) O(n3) 的时间复杂度,这是一种较高的复杂度,特别是对于大规模的矩阵。
Strassen 算法通过将两个矩阵分解成较小的子矩阵,并使用分治策略来减少乘法次数。在理论上,Strassen 算法的时间复杂度为 O ( n l o g 2 7 ) O(n^{log_27}) O(nlog27),约为 O ( n 2.807 ) O(n^{2.807}) O(n2.807)
但在实际中,并不总是比标准的 O(n^3) 算法表现更好,原因在于 Strassen 算法涉及多次递归,它的计算步骤涉及分解和合并子问题。这种递归的操作可能导致在计算大型矩阵乘法时,多次递归调用可能导致较多的缓存不命中,从而使得 Strassen 算法的实际性能不如预期。
import org.apache.commons.math3.linear.Array2DRowRealMatrix;
import org.apache.commons.math3.linear.RealMatrix;import java.util.Random;public class MatrixMultiplicationTest {public static void main(String[] args) {int n = 1000; // 矩阵大小 n x ndouble[][] A = new double[n][n];double[][] B = new double[n][n];// Fill the matrices with random valuesRandom random = new Random();for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {A[i][j] = random.nextDouble();B[i][j] = random.nextDouble();}}// Test Standard Matrix Multiplicationlong startTime = System.currentTimeMillis();double[][] C = standardMatrixMultiplication(A, B);long endTime = System.currentTimeMillis();System.out.println("Standard Matrix Multiplication time: " + (endTime - startTime) + " ms");// Test Strassen Matrix MultiplicationstartTime = System.currentTimeMillis();double[][] D = strassenMatrixMultiplication(A, B);endTime = System.currentTimeMillis();System.out.println("Strassen Matrix Multiplication time: " + (endTime - startTime) + " ms");}// Standard Matrix Multiplicationpublic static double[][] standardMatrixMultiplication(double[][] A, double[][] B) {int n = A.length;double[][] C = new double[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {for (int k = 0; k < n; k++) {C[i][j] += A[i][k] * B[k][j];}}}return C;}// Strassen Matrix Multiplicationpublic static double[][] strassenMatrixMultiplication(double[][] A, double[][] B) {// Convert input arrays to RealMatrixRealMatrix matrixA = new Array2DRowRealMatrix(A);RealMatrix matrixB = new Array2DRowRealMatrix(B);// Perform Strassen matrix multiplicationRealMatrix matrixC = matrixA.multiply(matrixB);// Convert the result back to 2D arrayreturn matrixC.getData();}
}
需要以下依赖
<dependency><groupId>org.apache.commons</groupId><artifactId>commons-math3</artifactId><version>3.6.1</version> <!-- 版本号可能需要根据您当前使用的版本进行调整 -->
</dependency>
测试结果
Standard Matrix Multiplication time: 11608 ms
Strassen Matrix Multiplication time: 25238 ms
总结
上面几个例子中的代码是非常粗糙,不严谨,有很多因素没有考虑,只是理解下缓存友好的意义,希望在实践中有这个意识。
相关文章:

缓存友好在实际编程中的重要性
引入 当CPU执行程序时,需要频繁地访问主存储器(RAM)中的数据和指令。然而,主存储器的访问速度相对较慢,与CPU的运算速度相比存在显著差异,每次都从主存中读取数据都会导致相对较长的等待时间,从…...
uni-ajax网络请求库使用
uni-ajax网络请求库使用 uni-ajax是什么 uni-ajax是基于 Promise 的轻量级 uni-app 网络请求库,具有开箱即用、轻量高效、灵活开发 特点。 下面是安装和使用教程 安装该请求库到项目中 npm install uni-ajax编辑工具类request.js // ajax.js// 引入 uni-ajax 模块 import ajax…...
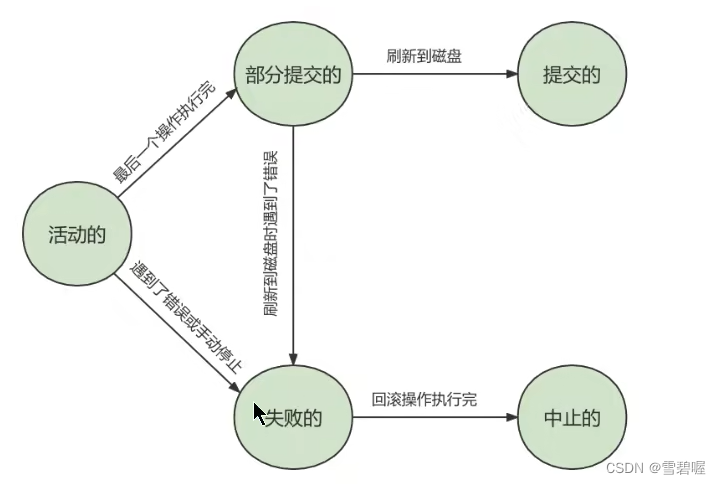
MYSQL进阶-事务
1.什么是数据库事务? 事务是一个不可分割的数据库操作序列,也是数据库并发控制的基本单位,其执 行的结果必须使数据库从一种一致性状态变到另一种一致性状态。事务是逻辑上 的一组操作,要么都执行,要么都不执行。 事务…...

python 常见数据类型和方法
不可变数据类型 不支持直接增删改 只能查 str 字符串 int 整型 bool 布尔值 None None型特殊常量 tuple 元组(,,,)回到顶部 可变数据类型,支持增删改查 list 列表[,,,] dic 字典{"":"","": ,} set 集合("",""…...

a-date-picker报错TypeError: date4.locale is not a function
问题描述 使用日期选择器,数据从后端获得,再赋值给a-date-picker做数据回显,遇到这个报错,排错后定位到a-date-picker组件本身接收数据的问题。 如果使用了dayjs或moment库来处理时间字符串,并且使用.format对时间数据…...
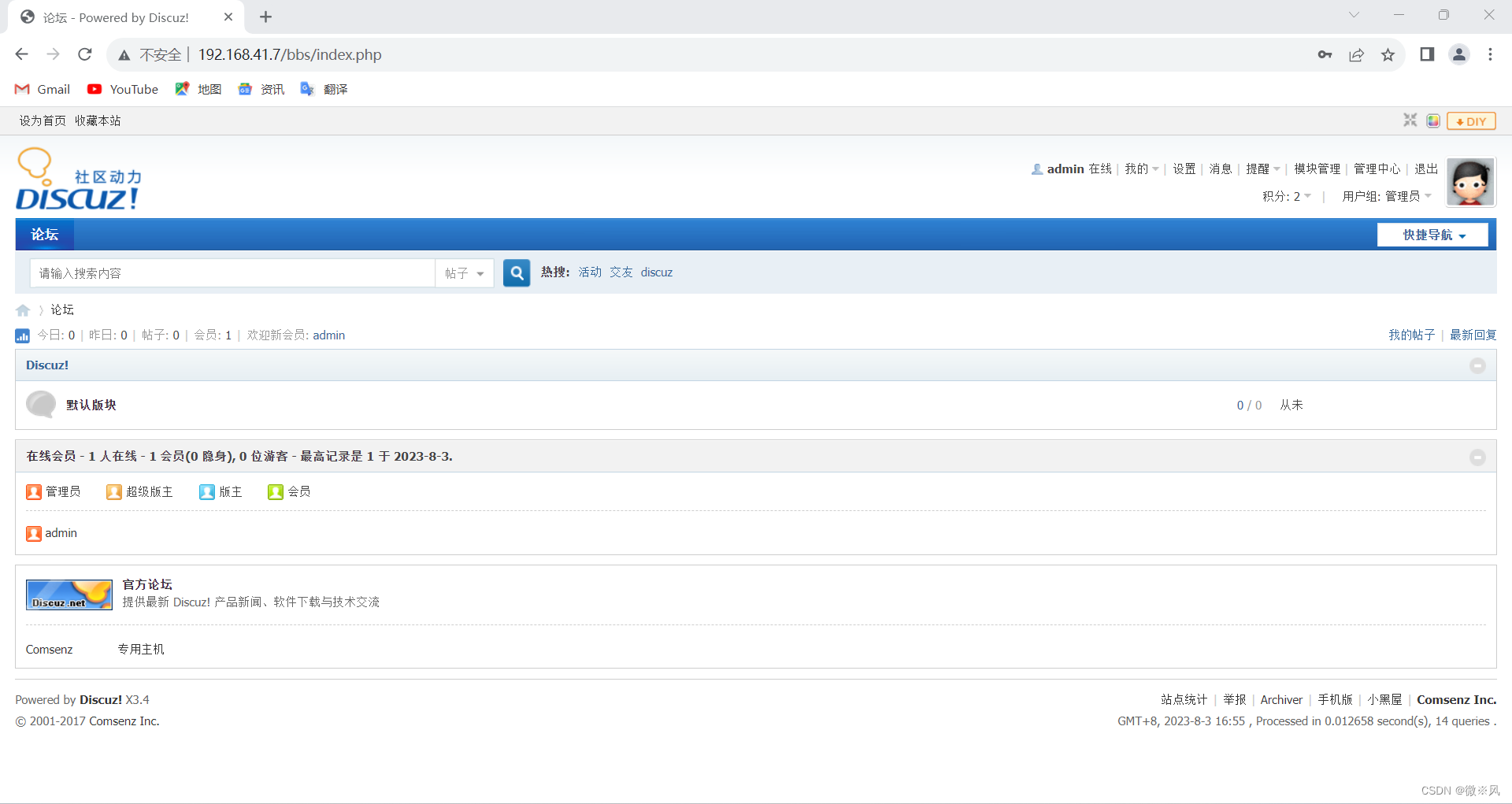
LNMP安装
目录 1、LNMP简述: 1.1、概述 1.2、LNMP是一个缩写词,及每个字母的含义 1.3、编译安装与yum安装差异 1.4、编译安装的优点 2、通过LNMP创建论坛 2.1、 安装nginx服务 2.1.1、关闭防火墙 2.1.2、创建运行用户 2.1.3、 编译安装 2.1.4、 优化路…...
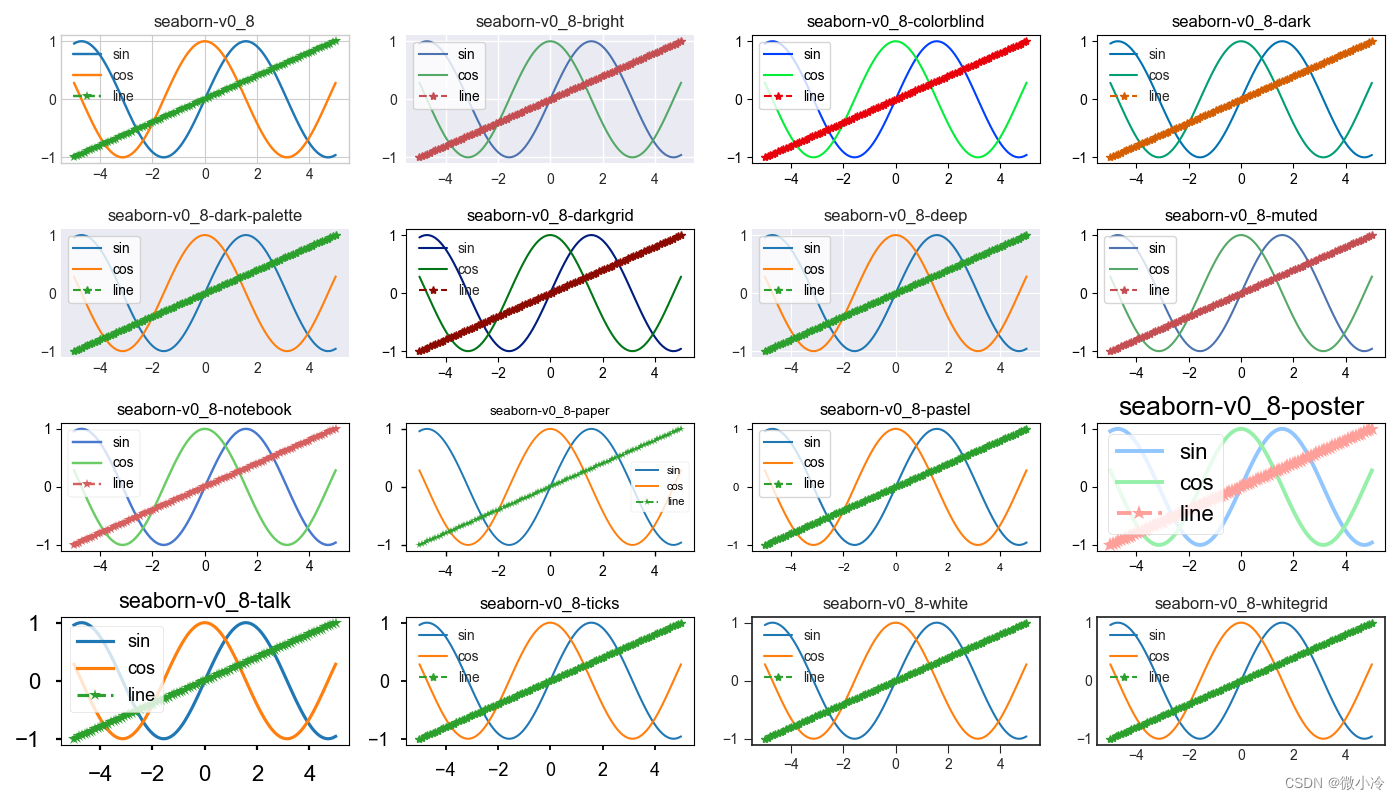
matplotlib绘图风格
文章目录 绘图风格测试代码默认和mpl风格复制风格seaborn风格 绘图风格 matplotlib功能强大,可以定制各种绘图要素,以满足个性化的绘图需求,而更换绘图风格也十分便捷,一个matplotlib.style.use函数轻松搞定,而可用的…...

【初级教程】Appium 启动应用 log 日志分析
刚开始学习 appium 时,老师给我布置了 appium 启动应用 log 分析的作业。由于工作比较忙,再者自己想先动手用 appium 写个公司的 app 的 UI 测试(目前简单的框架基本完成,在不断完善用例管理中)。写这篇文章是为了完成…...

FANUC机器人SRVO-300机械手断裂故障报警原因分析及处理办法
FANUC机器人SRVO-300机械手断裂故障报警原因分析及处理办法 首先,我们查看报警说明书上的介绍: 总结:即在机械手断裂设置为无效时,机器人检测出了机械手断裂信号(不该有的信号,现在检测到了,所以报警) 使机械手断裂设定为无效/有效的具体方法: 按下示教器的MENU菜单…...
MobPush iOS SDK iOS实时活动
开发工具:Xcode 功能需要: SwiftUI实现UI页面,iOS16.1以上系统使用 功能使用: 需应用为启动状态 功能说明 iOS16.1 系统支持实时活动功能,可以在锁定屏幕上实时获知各种事情的进展,MobPushSDK iOS 4.0.3版本已完成适配…...

c++开发模式,组合模式
组合模式,顾名思义,通过组合关系定义类间的关联关系,实现了将对象组合成树形结构,最终实现类的复用。可能是由于设计模式看的多了,初看组合模式的类图,感觉和装饰者模式类图很相似,都是使用继承…...

【GITHUB】FlipIt – Windows的开源翻页时钟
FlipIt 是一款免费开源的翻页时钟应用,专为 Windows 平台设计。该应用灵感来源于备受喜爱的老牌翻页时钟应用 Fliqlo,后者被公认为经典的翻页时钟屏保。然而,由于 Fliqlo 是基于 Flash 技术开发的,随着微软最近正式禁用 Flash&…...
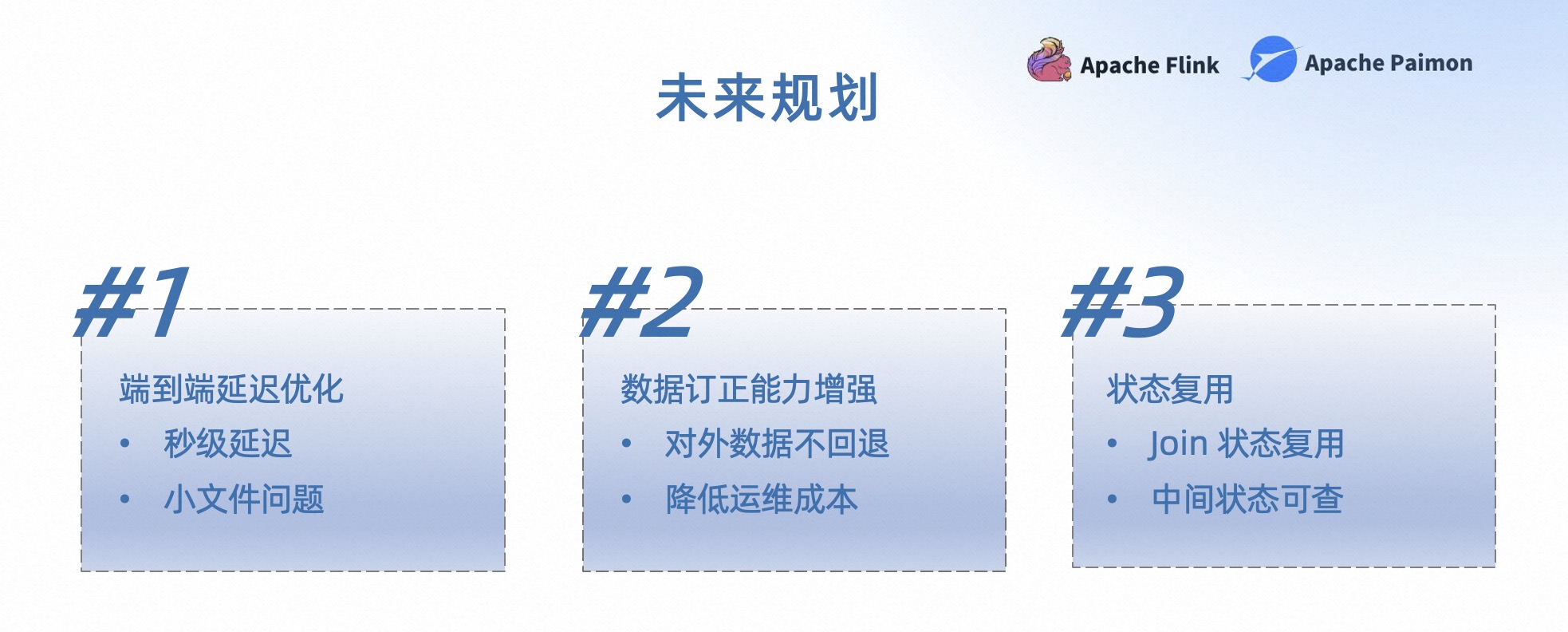
基于 Flink Paimon 实现 Streaming Warehouse 数据一致性管理
摘要:本文整理自字节跳动基础架构工程师李明,在 Apache Paimon Meetup 的分享。本篇内容主要分为四个部分: 背景 方案设计 当前进展 未来规划 点击查看原文视频 & 演讲PPT 一、背景 早期的数仓生产体系主要以离线数仓为主…...

云游戏App简记
注:在安卓手机端使用。其他端不做分析。 App手机游戏PC和主机游戏免费时长(手机游戏)是否排队备注咪咕快游支持。数量一般,和腾讯还有合作,有不少腾讯的游戏支持每日登录签到送30-60分钟,当天失效…...

ChatGPT已打破图灵测试,新的测试方法在路上
生信麻瓜的 ChatGPT 4.0 初体验 偷个懒,用ChatGPT 帮我写段生物信息代码 代码看不懂?ChatGPT 帮你解释,详细到爆! 如果 ChatGPT 给出的的代码不太完善,如何请他一步步改好? 全球最佳的人工智能系统可以通过…...
)
Flask学习笔记_异步CMS(五)
Flask学习笔记_异步CMS(五) 1.环境1.安装nvm2.安装node 2.使用vue-cli创建项目3.安装相关插件4.后台CMS开发1.页面结构1.app.vue搭建结构2.element-icon组件的使用3.iconfont组件的使用 2.使用[Vue-router](https://router.vuejs.org/installation.html)…...

争夺年度智能汽车「中间件」方案提供商TOP10,谁率先入围
进入2023年,整车电子架构升级进入新周期,无论是智能驾驶、智能座舱、车身控制还是信息网络安全,软件赋能仍是行业的主旋律。 作为智能汽车赛道的第三方研究咨询机构,高工智能汽车研究院持续帮助车企、投资机构挖掘具备核心竞争力…...

【Spring Cloud一】微服务基本知识
系列文章目录 微服务基本知识 系列文章目录前言一、系统架构的演变1.1单体架构1.2分层架构1.3分布式架构1.4微服务架构1.5分布式、SOA、微服务的异同点 二、CAP原则三、RESTfulRESTful的核心概念: 四、共识算法 前言 在实际项目开发过程中,目前负责开发…...

swift - 如何在数组大小更改后刷新 ForEach 显示元素的数量(SwiftUI、Xcode 11 Beta 5)
我正在尝试实现一个 View ,该 View 可以在内容数组的大小发生变化时更改显示项目的数量(由 ForEach 循环创建),就像购物应用程序可能会在用户下拉刷新后更改其可用项目的数量一样 这是我到目前为止尝试过的一些代码。如果我没记错的话,这些适…...

编程导航算法村第七关 |二叉树的遍历
编程导航算法村第七关 | 二叉树的遍历 前序遍历(递归) public List<Integer> preorderTraversal(TreeNode root) {ArrayList<Integer> result new ArrayList<Integer>();preorder(root, result);return result;}public void preorde…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
