信息学奥赛一本通——1156:求π的值
文章目录
- 题目
- 【题目描述】
- 【输入】
- 【输出】
- 【输入样例】
- 【输出样例】
- AC代码
题目
【题目描述】
根据公式:
a r c t a n x ( x ) = x − x 3 3 + x 5 5 − x 7 7 + ⋯ arctanx\left ( x \right ) = x- \frac{x^3}{3} + \frac{x^5}{5}-\frac{x^7}{7}+ \cdots arctanx(x)=x−3x3+5x5−7x7+⋯
$arctanx\left ( x \right ) = x- \frac{x^3}{3} + \frac{x^5}{5}-\frac{x^7}{7}+ \cdots$
定义函数 a r c t a n x ( x ) arctanx\left ( x \right ) arctanx(x),,求当最后一项小于 1 0 − 6 10^{-6} 10−6时 π \pi π的值
【输入】
(无)
【输出】
π \pi π的值。保留到小数点后 10 10 10位。
【输入样例】
(无)
【输出样例】
(无)
AC代码
1:
函数
#include<bits/stdc++.h>
using namespace std;
double arctanx(double n){double sum=0,temp=n;int i=1;while(fabs(temp/i)>1e-6){sum+=temp/i;i+=2;temp=-1*n*n*temp;}return sum;
}
int main() {double y=6.0*arctanx(1.0/sqrt(3));cout<<fixed<<setprecision(10)<<y;return 0;
}
2:
直接输出答案
#include<bits/stdc++.h>
using namespace std;
int main() {cout<<"3.1415905109";return 0;
}
相关文章:

信息学奥赛一本通——1156:求π的值
文章目录 题目【题目描述】【输入】【输出】【输入样例】【输出样例】 AC代码 题目 【题目描述】 根据公式: a r c t a n x ( x ) x − x 3 3 x 5 5 − x 7 7 ⋯ arctanx\left ( x \right ) x- \frac{x^3}{3} \frac{x^5}{5}-\frac{x^7}{7} \cdots arctanx(x…...

BI报表工具有哪些作用?奥威BI全面剖析数据
BI报表工具有哪些作用?主要的作用是通过整合多业务来源数据,全面分析挖掘数据,来帮助企业实现数据化运营、支持智能决策、实现数据资产沉淀和增值、进行数据挖掘和预测分析、提高数据可读性和数据可视化程度等,从而提高企业的竞争…...

【云原生K8s】初识Kubernetes的理论基础
K8S由google的Borg系统(博格系统,google内部使用的大规模容器编排工具)作为原型,后经GO语言延用Borg的思路重写并捐献给CNCF基金会开源。 云原生基金会(CNCF)于2015年12月成立,隶属于Linux基金会。CNCF孵化的第一个项目…...
:jdk8之前的日期API)
javaAPI(三):jdk8之前的日期API
jdk 8之前的日期时间API 1、System类中currentTimeMillis()。 2、 java.util.Date和子类java.sql.Date。 3、SimpleDateFormat 4、Calendar System返回时间戳 long time System.currentTimeMillis();System.out.println(time);Date类 java.util.Date类 实例化 构造器一&a…...

驱动开发(中断)
头文件: #ifndef __LED_H__ #define __LED_H__#define PHY_LED1_MODER 0X50006000 #define PHY_LED1_ODR 0X50006014 #define PHY_LED1_RCC 0X50000A28#define PHY_LED2_MODER 0X50007000 #define PHY_LED2_ODR 0X50007014 #define PHY_LED2_RCC 0X50000A28#def…...

TypeScript最新语法总结
注意注意!!!本文介绍的是最新的TypeScript4的重要语法 第一部分:TypeScript的简介 TypeScript 是由微软开发的一款开源的编程语言,TypeScript 是 Javascript 的超集,遵循最新的 ES6、ES5 规范,…...
sentinel组件
目录 定义 4.加SentinelResource,blockHander是超过阈值之后执行的函数 5.设置阈值 6.springboot集成sentinel 定义 1.sentinel知道当前流量大小,在浏览器和后端之间加sentinel控制流量,避免大批量的瞬时请求都达到服务上,将服务压垮 2.…...
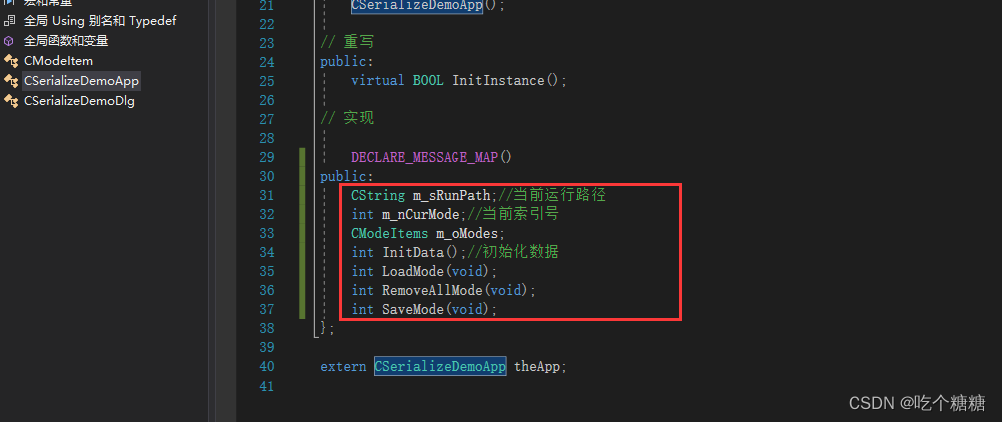
26 MFC序列化函数
文章目录 Serialize对于存储文件的序列化 Serialize Serialize 是一个在 MFC (Microsoft Foundation Classes) 中常用的函数或概念。它用于将对象的数据进行序列化和反序列化,便于在不同的场景中保存、传输和恢复对象的状态。 在 MFC 中,Serialize 函数…...
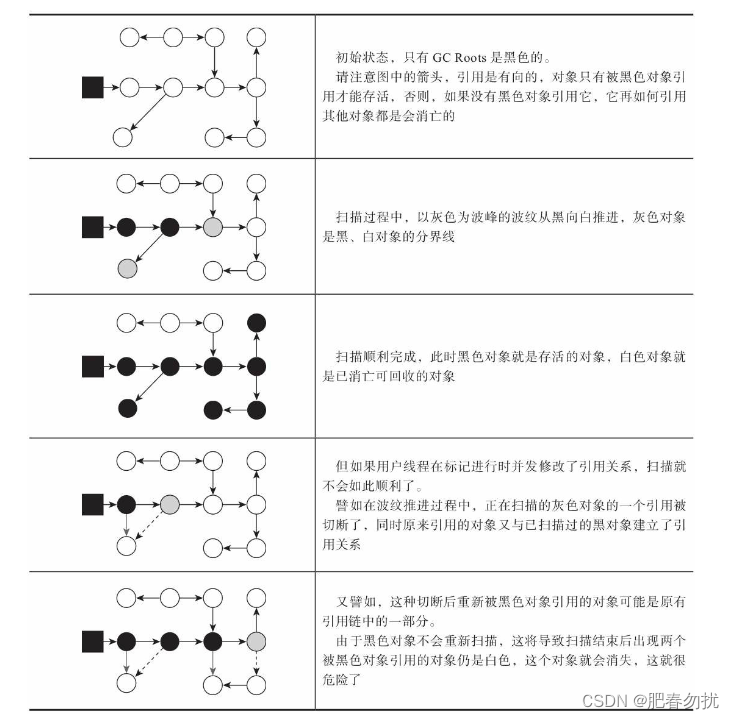
GC 深入(小白,对gc有一个进一步的了解)
垃圾回收器的搭配 一般固定 一般这年轻代垃圾回收器,老年代垃圾回收器,如上图搭配着使用 1.8呢默认就是最后边那哥俩 jvm调优 一个就是增加吞吐量 一个就是减少STW的时间。 三色标记算法(理解根可达算法) 并发的可达性分析 有…...

CSS前端面试
文章目录 rem、em、vh、px各自代表的含义?盒模型poison 定位属性flex属性让元素水平垂直居中页面适配的方法有哪些 rem、em、vh、px各自代表的含义? px:绝对单位,页面按精确像素展示 em:相对单位,基准点为…...

VB+SQL餐饮管理系统设计与实现
第一章 前言 1.1 绪论 当今世界已进入了在计算机信息管理领域中激烈竞争的时代,应用计算机已经变得十分普遍了,如同我们离不开的自行车、汽车一样。我们应该承认,谁掌握的知识多,信息量大,信息处理速度快,批量大,谁的效率就高,谁就能够在各种竞争中立于不败之地。随着…...
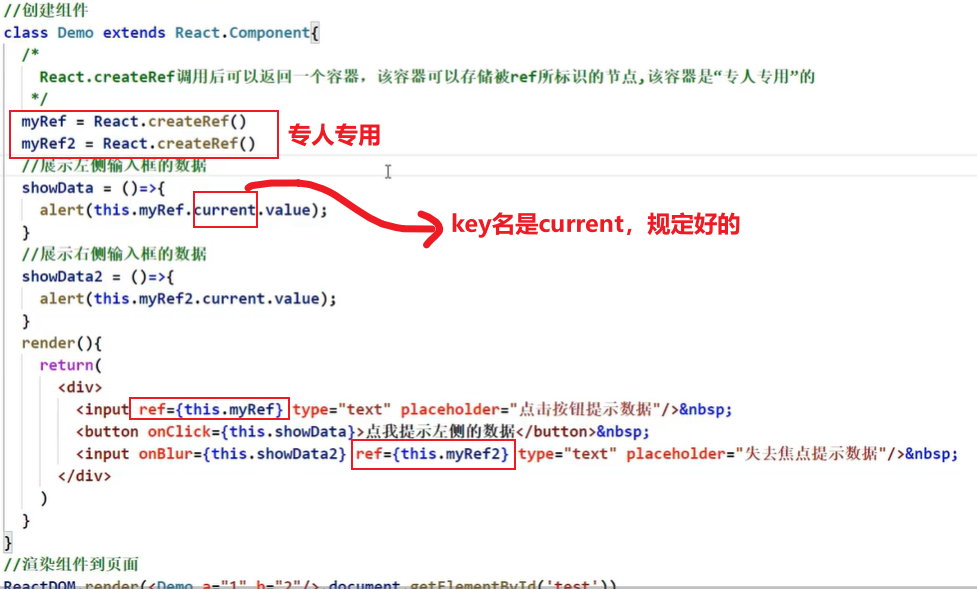
React入门学习笔记2
jsx语法规则 定义虚拟DOM时,不要写引号。标签中混入JS表达式时要用{ }。样式的类名指定不要用class,要用className。内联样式,要用style{{key:value}}的形式去写。只有一个根标签标签必须闭合标签首字母 )若小写字母开头…...

Palo Alto Networks® PA-220R 下一代防火墙 确保恶劣工况下的网络安全
一、主要安全功能 1、每时每刻在各端口对全部应用进行分类 • 将 App-ID 用于工业协议和应用,例如 Modbus、 DNP3、IEC 60870-5-104、Siemens S7、OSIsoft PI 等。 • 不论采用何种端口、SSL/SSH 加密或者其他规避技术,都会识别应用。 • 使用…...

架构训练营学习笔记:5-2 负载均衡架构
多级负载架构 设计关键点 性能需求、维护复杂度之间做取舍。 一可以去掉F5、LVS : F5 是成本较高,LVS 是复杂,对于性能没那么高需求,可以去掉。 二 去掉ng: 服务网关服务 适应于初创公司快速验证,内部的 小系统…...
二叉树的性质、前中后序遍历【详细】
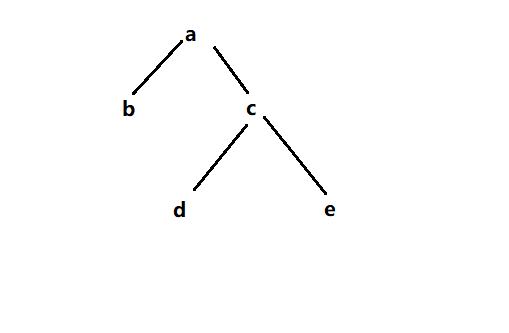
1. 树概念2.二叉树的概念1.2二叉树的性质 3.二叉树遍历3.2前序遍历3.2 中序遍历3.3 后序遍历 1. 树概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合,有二叉树,N叉树等等。 子树…...

涨姿势了,有意思的气泡 Loading 效果
今日,群友提问,如何实现这么一个 Loading 效果: 这个确实有点意思,但是这是 CSS 能够完成的? 没错,这个效果中的核心气泡效果,其实借助 CSS 中的滤镜,能够比较轻松的实现࿰…...
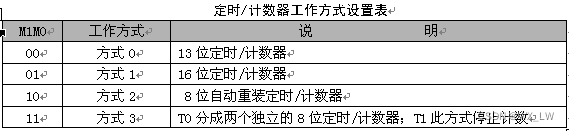
单片机中断系统
单片机中断系统 中断的概念: CPU在处理某一事件A时,发生了另一事件B请求CPU迅速去处理(中断发生);CPU暂时中断当前的工作,转去处理事件B(中断响应和中断服务);待CPU将事…...
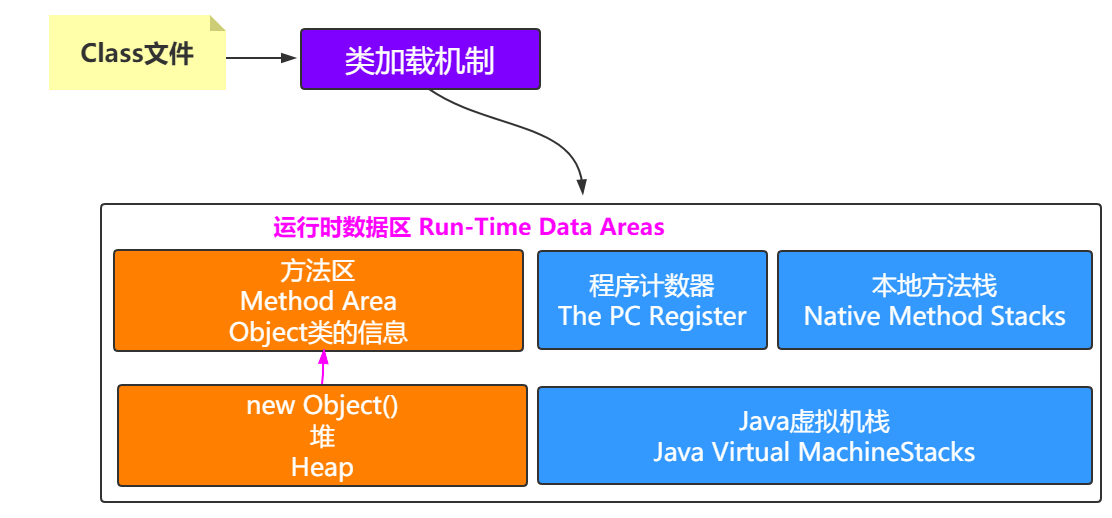
二、JVM-深入运行时数据区
深入运行时数据区 计算机体系结构 JVM的设计实际上遵循了遵循冯诺依曼计算机结构 CPU与内存交互图: 硬件一致性协议: MSI、MESI、MOSI、Synapse、Firely、DragonProtocol 摩尔定律 摩尔定律是由英特尔(Intel)创始人之一戈登摩尔(Gordon Moore)提出来…...

随机验证码vue实现,登录验证码随机验证码数字和字母类型的
1、组件 <!--loginCode登录验证码组件--> <template> <canvas id"canvasCode" :width"contentWidth" :height"contentHeight" /> </template> <script> export default { name: LoginCode, props: { identif…...
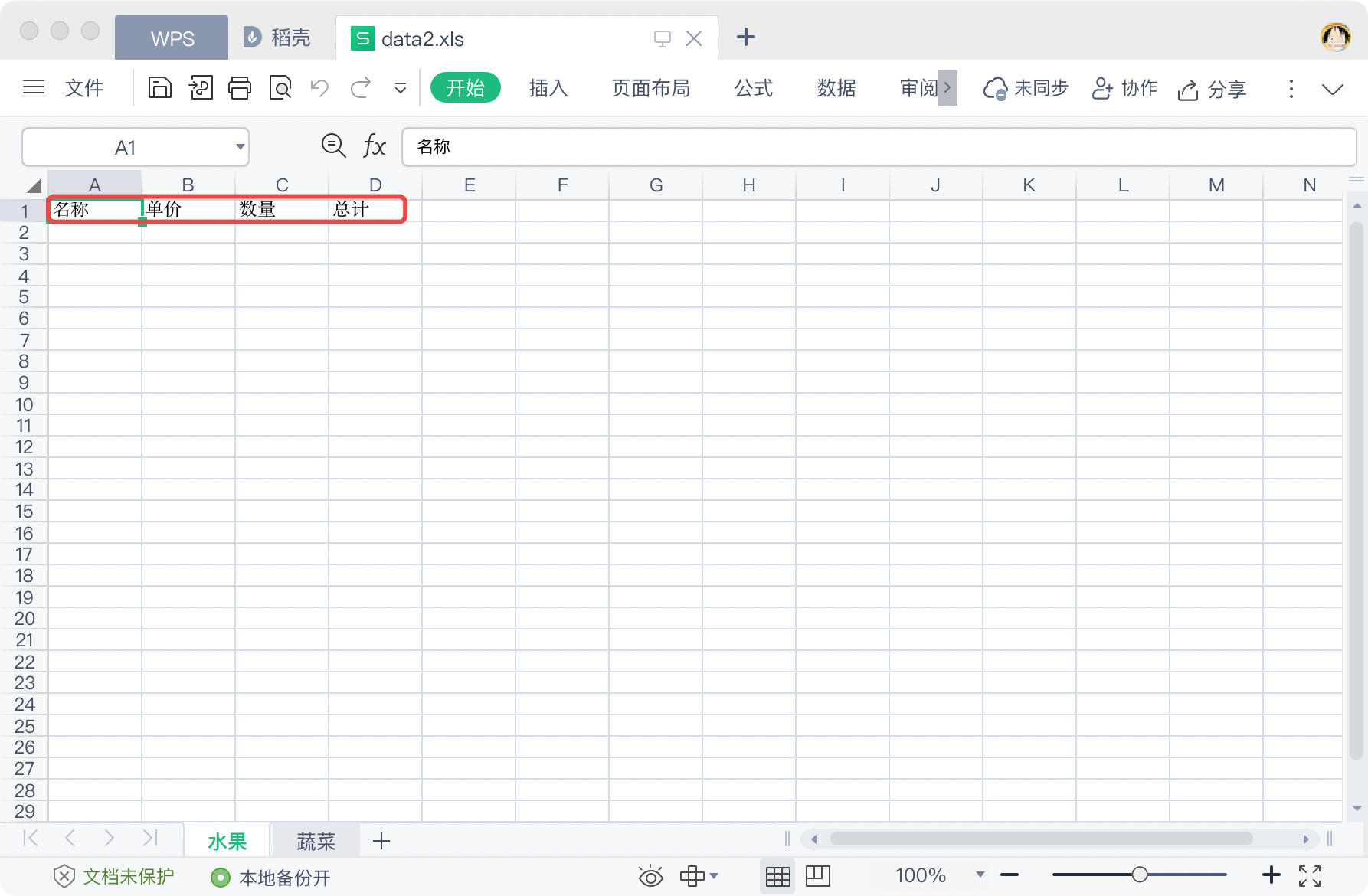
xlrd与xlwt操作Excel文件详解
Python操作Excel的模块有很多,并且各有优劣,不同模块支持的操作和文件类型也有不同。下面是各个模块的支持情况: .xls.xlsx获取文件内容写入数据修改文件内容保存样式调整插入图片xlrd√√√xlwt√√√√√xlutils√√√√xlwings√√√√√…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
