【数据结构OJ题】合并两个有序数组
原题链接:https://leetcode.cn/problems/merge-sorted-array/
目录
1. 题目描述
2. 思路分析
3. 代码实现
1. 题目描述

2. 思路分析
看到这道题,我们注意到nums1[ ]和nums2[ ]两个数组都是非递减的。所以我们很容易想到额外开一个数组tmp[ ],依次比较两个数组的元素,每次取小的尾插到新数组tmp[ ]即可。但是这需要额外再开空间。



也有一种方法是将这两个数组的元素都拷贝到一起,然后使用qsort排序 复杂度为O(NlogN)。
显然这两种方法的复杂度都不够优秀,是否有更好的方法呢?
我们可以倒着比较,取大的依次往前插入。等到有一个数组被遍历完,就结束。
因为两个数组都是非递减的,nums1[ ]数组的长度比nums2[ ]大,所以如果nums1[ ]先被遍历完,就将nums2[ ]没有被遍历的元素直接拷贝到nums1[ ]前面。
如果nums2[ ]先被遍历完,则不用额外操作(因为nums1[ ]整体本身就是非递减的,所以那些没有被遍历到的元素也是按非递减排列的)。
流程演示:


3. 代码实现
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {int end1 = m - 1, end2 = n - 1, end = m + n - 1;while (end1 >= 0 && end2 >= 0){if (nums1[end1] >= nums2[end2])nums1[end--] = nums1[end1--];elsenums1[end--] = nums2[end2--];}while (end2 >= 0)nums1[end--] = nums2[end2--];
}
相关文章:

【数据结构OJ题】合并两个有序数组
原题链接:https://leetcode.cn/problems/merge-sorted-array/ 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 看到这道题,我们注意到nums1[ ]和nums2[ ]两个数组都是非递减的。所以我们很容易想到额外开一个数组tmp[ ]&#x…...
数据结构笔记--归并排序及其拓展题(小和问题、逆序对问题)
目录 1--归并排序 2--小和问题 3--逆序对问题 1--归并排序 归并排序的核心思想:将一个无序的序列归并排序为一个有序的系列;通过递归将无序的序列二分,从底层开始将二分的序列归并排序为有序序列; #include <iostream> #…...

flutter开发实战-实现css线性渐变转换flutter渐变LinearGradient功能
flutter开发实战-实现css线性渐变转换flutter渐变LinearGradient功能 在之前项目开发中,遇到更换样式,由于从服务器端获取的样式均为css属性值,需要将其转换成flutter类对应的属性值。这里只处理线性渐变linear-gradient 比如渐变 “linear-…...

python推理小游戏bagels
python推理小游戏bagels bagels是一个推理小游戏,你的朋友想到一个随机的、没有重复的3位数字,你尝试去猜测它是什么。每次猜测之后,朋友就会给出3中类型的线索: Bagels: 你猜测的3个数都不在神秘数字中;Pico&#x…...

DBSCAN聚类
一、概述 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法,簇集的划定完全由样本的聚集程度决定。聚集程度不足以构成簇落的那些样本视为噪声点,因此DBSCAN聚类的方式也可以用于异常点的检测。 二、算法…...

java+ssm美食推荐交流系统 7jsw7
随着社会的发展,美食推荐系统的管理形势越来越严峻。越来越多的用户利用互联网获得信息,但美食推荐信息鱼龙混杂,真假难以辨别。为了方便用户更好的获得美食推荐信息,因此,设计一款安全高效的美食推荐系统极为重要。 为…...

基于php雪花算法工具类Snowflake -来自chatGPT
<?phpclass Snowflake {// 定义Snowflake算法的各个参数private $workerIdBits 5;private $datacenterIdBits 5;private $sequenceBits 12;private $workerIdShift;private $datacenterIdShift;private $timestampLeftShift;private $maxWorkerId;private $maxDatacente…...

怎么加密文件夹才更安全?安全文件夹加密软件推荐
文件夹加密可以让其中数据更加安全,但并非所有加密方式都能够提高极高的安全强度。那么,怎么加密文件夹才更安全呢?下面我们就来了解一下那些安全的文件夹加密软件。 文件夹加密超级大师 如果要评选最安全的文件夹加密软件,那么文…...

知识分享和Tomcat简单部署press应用
一、简述静态网页和动态网页的区别。 静态网页: 静态网页是指运行于客户端的程序、网页、组件、纯粹HTML格式的网页; 如果有涉及网页内容的修改,就要修改源文件,重新上传到服务器。而且当网站信息量很大的时候,网页制作和维护都非常困…...

回归预测 | MATLAB实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元多输入单输出回归预测
回归预测 | MATLAB实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元多输入单输出回归预测 目录 回归预测 | MATLAB实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元多输入单输出回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SO-CNN-BiGRU蛇群算法…...
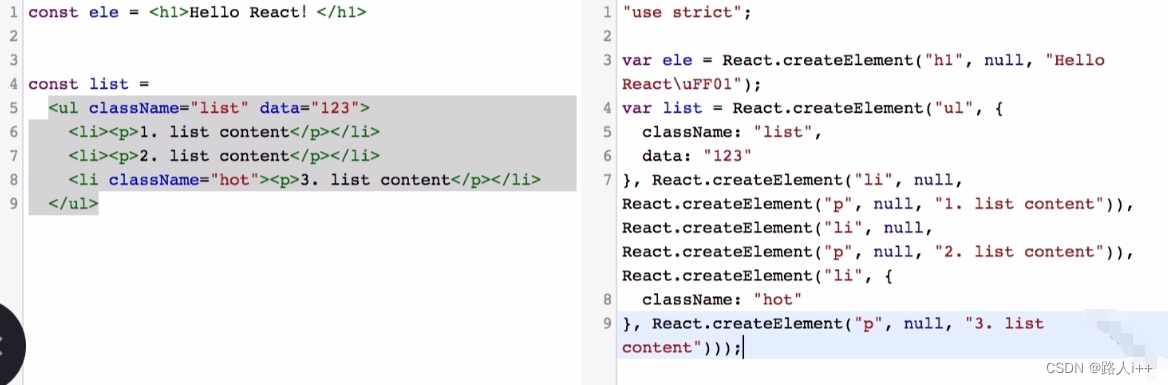
步入React前厅 - 组件和JSX
目录 扩展学习资料 购物车应用 编写React元素 /src/index.js 创建组件 /src/components/listItem.jsx /src/App.js 理解JSX【JavaScriptXML】 JSX是什么 JSX规则 /src/components/listItem.jsx 使用Fragments /src/App.js 为何要使用Fragments 表格中使用Fragme…...
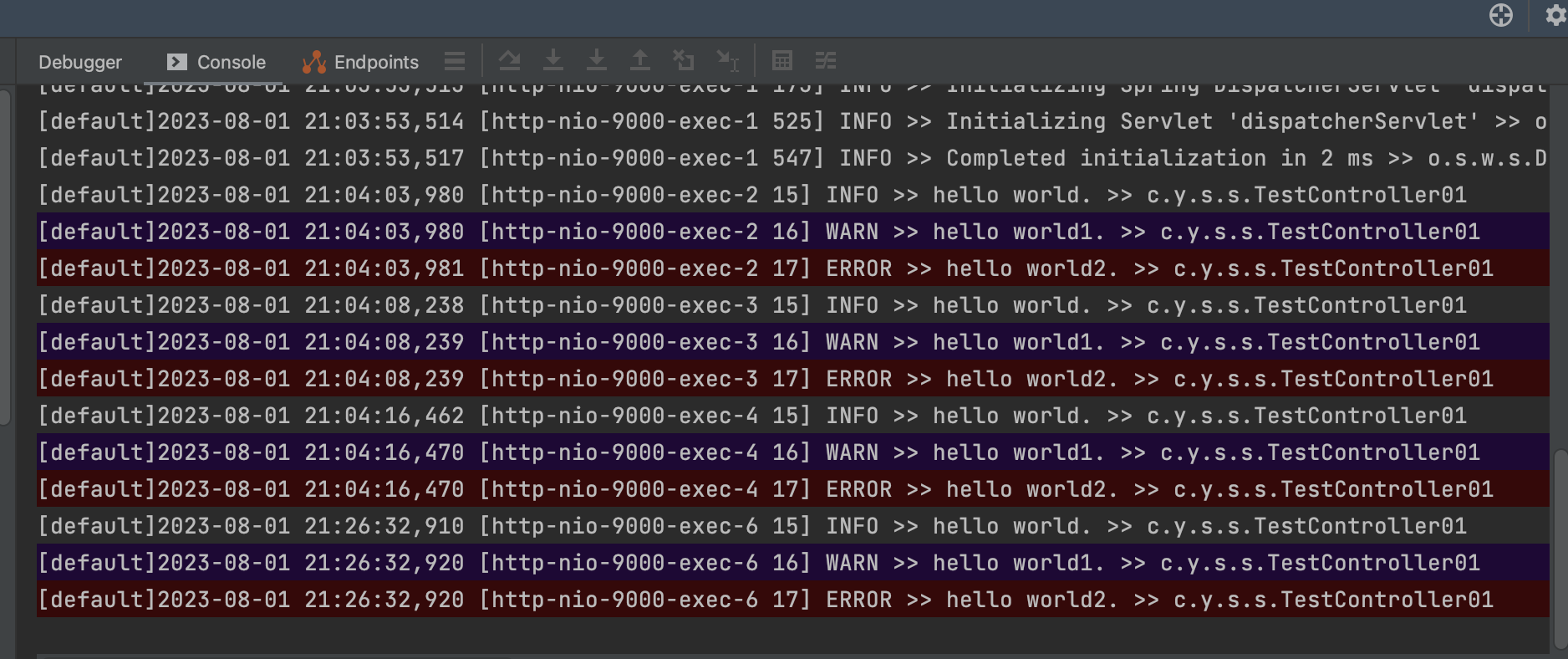
SpringBoot整合Sfl4j+logback的实践
一、概述 对于一个web项目来说,日志框架是必不可少的,日志的记录可以帮助我们在开发以及维护过程中快速的定位错误。slf4j,log4j,logback,JDK Logging等这些日志框架都是我们常见的日志框架,本文主要介绍这些常见的日志框架关系和SpringBoot…...

IT 基础架构自动化
什么是 IT 基础架构自动化 IT 基础架构自动化是通过使用技术来控制和管理构成 IT 基础架构的软件、硬件、存储和其他网络组件来减少人为干预的过程,目标是构建高效、可靠的 IT 环境。 为什么要自动化 IT 基础架构 为客户和员工提供无缝的数字体验已成为企业的当务…...
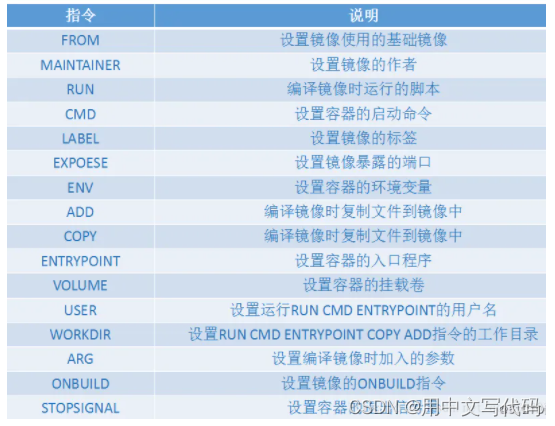
Docker入门——保姆级
Docker概述 —— Notes from WAX through KuangShen 准确来说,这是一篇学习笔记!!! Docker为什么出现 一款产品:开发—上线 两套环境!应用环境如何铜鼓? 开发 – 运维。避免“在我的电脑…...

MONGODB ---- Austindatabases 历年文章合集
开头还是介绍一下群,如果感兴趣polardb ,mongodb ,mysql ,postgresql ,redis 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请联系 liuaustin3 ,在新加的朋友会分到2群(共…...
菠萝头 pinia和vuex对比 pinia比vuex更香 Pinia数据持久化及数据加密
前言 毕竟尤大佬都推荐使用pinia,支持vue2和vue3! 如果熟悉vuex,花个把小时把pinia看一下,就不想用vuex了 支持选项式api和组合式api写法pinia没有mutations,只有:state、getters、actionspinia分模块不…...

机器学习笔记 - 关于GPT-4的一些问题清单
一、简述 据报道,GPT-4 的系统由八个模型组成,每个模型都有 2200 亿个参数。GPT-4 的参数总数估计约为 1.76 万亿个。 近年来,得益于 GPT-4 等高级语言模型的发展,自然语言处理(NLP) 取得了长足的进步。凭借其前所未有的规模和能力,GPT-4为语言 AI设立了新标准,并为机…...

sql 参数自动替换
需求:看日志时,有的sql 非常的长,参数比较多,无法直接在sql 客户端工具执行,如果一个一个的把问号占位符替换为参数太麻烦,因此写个html 小工具,批量替换: 代码: <!…...
Linux——设备树
目录 一、Linux 设备树的由来 二、Linux设备树的目的 1.平台识别 2.实时配置 3.设备植入 三、Linux 设备树的使用 1.基本数据格式 2.设备树实例解析 四、使用设备树的LED 驱动 五、习题 一、Linux 设备树的由来 在 Linux 内核源码的ARM 体系结构引入设备树之前&#x…...
网络:从socket编程的角度说明UDP和TCP的关系,http和tcp的区别
尝试从编程的角度解释各种网络协议。 UDP和TCP的关系 从Python的socket编程角度出发,UDP(User Datagram Protocol)和TCP(Transmission Control Protocol)是两种不同的传输协议。 TCP是一种面向连接的协议,…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
