机器学习深度学习——序列模型(NLP启动!)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——卷积神经网络(LeNet)
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
现在多多少少是打下了一点基础了,因为我的本科毕业论文是NLP方向的,所以现在需要赶忙打好NLP模型所需要的知识,然后实现一些NLP方向的科研项目,用于我的9月份预推免。就剩一个月就要开始预推免了,大家一起加油!
序列模型
- 引入
- 统计工具
- 自回归模型
- 马尔可夫模型
- 因果关系
- 训练
- 预测
- 总结
引入
对于一部电影,随着时间的推移,人们对电影的看法会发生很大的变化。也就是说,因为时间上的连续性,一些事情的发生也是会互相影响的,如果这些序列重排就会失去意义。有几个例子:
1、音乐、语音、文本和视频都是连续的。
2、地震具有很强的相关性,即大地震发生后,很可能会有几次小余震。
3、人类之间的互动也是连续的,比如微博上互相打口水仗。
4、预测明天的股价要比过去的股价更困难(先见之明比时候诸葛亮要更难)。
统计工具
我们可以通过下式来进行预测:
x t 符合 P ( x t ∣ x t − 1 , . . . , x 1 ) x_t符合P(x_t|x_{t-1},...,x_1) xt符合P(xt∣xt−1,...,x1)
其中,x是非独立同分布的,因为时间上具有连续性,导致不同时间上的预测可能也会有相关性
自回归模型
从上面的式子可以看出,数据的数量随着t而变化:输入数据的数量这个数字将会随着我们遇到的数据量的增加而增加。因此我们需要使得这个计算更加简单,有两种策略:
1、自回归模型
假设显示情况下,相当长的序列
x t − 1 , . . . , x 1 x_{t-1},...,x_1 xt−1,...,x1
可能不是必要的,我们只需要满足某个长度τ的时间跨度,即使用观测序列
x t − 1 , . . . , x t − τ x_{t-1},...,x_{t-τ} xt−1,...,xt−τ
这样的好处是参数的数量总是不变的,至少在t>τ的时候是这样的,既然都是固定长度,那么我们就可以训练之前讲过的几乎所有模型了(线性模型,或者多层感知机等等)。这种模型被称为自回归模型,因此总是队自己执行回归。
2、潜变量自回归模型
如下图所示:
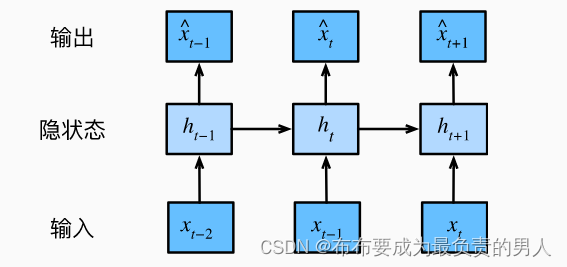
该图体现出,我们需要保留和更新对过去观测的总结:
h t h_t ht
并且同时更新预测
x t ^ \hat{x_t} xt^
这就产生了基于
x t ^ = P ( x t ∣ h t ) \hat{x_t}=P(x_t|h_t) xt^=P(xt∣ht)
的估计,以及公式
h t = g ( h t − 1 , x t − 1 ) h_t=g(h_{t-1},x_{t-1}) ht=g(ht−1,xt−1)
更新的模型。
而由于h从未被观测到,所以这类模型也叫作潜变量自回归模型。
而整个序列的估计值都将通过以下方式获得:
P ( x 1 , . . . , x T ) = ∏ t = 1 T P ( x t ∣ x t − 1 , . . . , x 1 ) P(x1,...,x_T)=\prod_{t=1}^TP(x_t|x_{t-1},...,x_1) P(x1,...,xT)=t=1∏TP(xt∣xt−1,...,x1)
马尔可夫模型
我们之前在估计的时候,选择的是在当前时序的前τ个数,只要和当前时序之前的所有数计算得来的结果近似,就说序列满足马尔可夫条件。特别是当τ=1时,得到一个一阶马尔可夫模型:
P ( x ) = P ( x 1 , . . . , x T ) = ∏ t = 1 T P ( x t ∣ x t − 1 ) 当 P ( x 1 ∣ x 0 ) = P ( x 1 ) P(x)=P(x_1,...,x_T)=\prod_{t=1}^TP(x_t|x_{t-1})当P(x_1|x_0)=P(x_1) P(x)=P(x1,...,xT)=t=1∏TP(xt∣xt−1)当P(x1∣x0)=P(x1)
因果关系
原则上,将P(x)倒序展开也没啥问题,可以基于条件概率公式写成:
P ( x 1 , . . . , x T ) = ∏ t = T 1 P ( x t ∣ x t + 1 , . . . , x T ) P(x_1,...,x_T)=\prod_{t=T}^1P(x_t|x_{t+1},...,x_T) P(x1,...,xT)=t=T∏1P(xt∣xt+1,...,xT)
但是在物理上这并不好实现,毕竟理论上一般没有根据未来的事情推测过去的事情。
训练
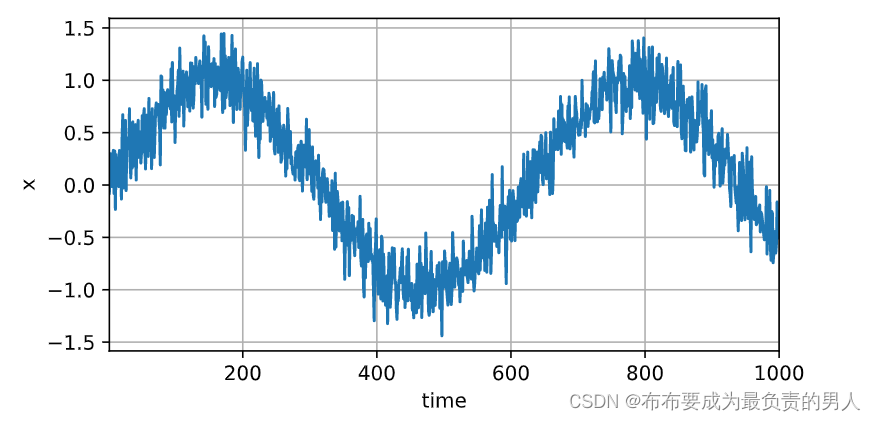
首先生成一些数据,使用正弦函数和一些可加性噪声来生成序列数据。(现在开始用notebook了)
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2lT = 1000 # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))
接下来,将该序列转换为特征-标签对,这里我们使用前600个“特征-标签”对进行训练:
tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),batch_size, is_train=True)
在这里,我们使用一个相当简单的架构训练模型: 一个拥有两个全连接层的多层感知机,ReLU激活函数和平方损失。
# 初始化网络权重的函数
def init_weights(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)# 一个简单的多层感知机
def get_net():net = nn.Sequential(nn.Linear(4, 10),nn.ReLU(),nn.Linear(10, 1))net.apply(init_weights)return net# 平方损失。注意:MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')
下面开始训练模型:
def train(net, train_iter, loss, epochs, lr):trainer = torch.optim.Adam(net.parameters(), lr) # 一种内置的优化器,可自行去了解for epoch in range(epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, 'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')net = get_net()
train(net, train_iter, loss, 5, 0.01)
运行结果:
epoch 1, loss: 0.061968
epoch 2, loss: 0.054118
epoch 3, loss: 0.051940
epoch 4, loss: 0.050062
epoch 5, loss: 0.050939
预测
训练损失看起来不大,那我们可以开始进行单步预测(也就是检查模型预测下一个时间步的能力):
onestep_preds = net(features)
d2l.plot([time, time[tau:]],[x.detach().numpy(), onestep_preds.detach().numpy()], 'time','x', legend=['data', '1-step preds'], xlim=[1, 1000],figsize=(6, 3))
结果:
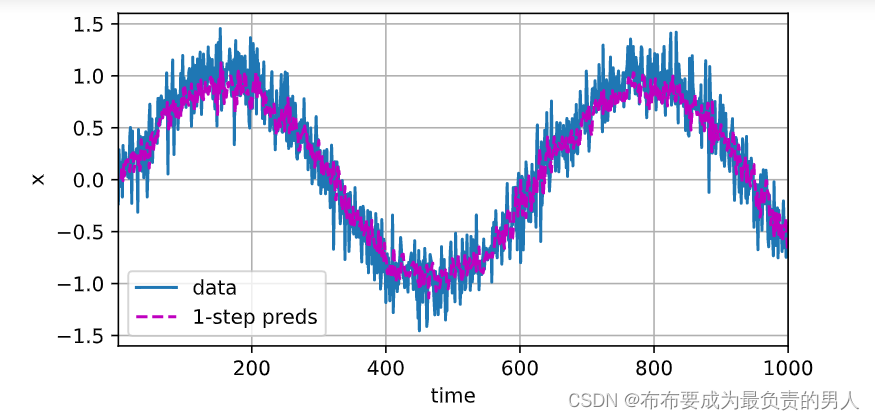
单步预测的效果不错,即便预测的时间步超过了600+4(n_train+tau),结果看起来也还是可以的,但是如果我们继续向前迈进,那么接下来的预测值就要基于之前的预测值和原本值或者完全基于之前的预测值,即:
x ^ 605 = f ( x 601 , x 602 , x 603 , x 604 ) x ^ 606 = f ( x 602 , x 603 , x 604 , x ^ 605 ) x ^ 607 = f ( x 603 , x 604 , x ^ 605 , x ^ 606 ) x ^ 608 = f ( x 604 , x ^ 605 , x ^ 605 , x ^ 607 ) x ^ 609 = f ( x ^ 605 , x ^ 606 , x ^ 607 , x ^ 608 ) \hat{x}_{605}=f(x_{601},x_{602},x_{603},x_{604})\\ \hat{x}_{606}=f(x_{602},x_{603},x_{604},\hat{x}_{605})\\ \hat{x}_{607}=f(x_{603},x_{604},\hat{x}_{605},\hat{x}_{606})\\ \hat{x}_{608}=f(x_{604},\hat{x}_{605},\hat{x}_{605},\hat{x}_{607})\\ \hat{x}_{609}=f(\hat{x}_{605},\hat{x}_{606},\hat{x}_{607},\hat{x}_{608}) x^605=f(x601,x602,x603,x604)x^606=f(x602,x603,x604,x^605)x^607=f(x603,x604,x^605,x^606)x^608=f(x604,x^605,x^605,x^607)x^609=f(x^605,x^606,x^607,x^608)
因此我们必须使用我们自己的预测(而不是原始数据)来进行多步预测:
multistep_preds = torch.zeros(T)
multistep_preds[: n_train + tau] = x[: n_train + tau]
for i in range(n_train + tau, T):multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))d2l.plot([time, time[tau:], time[n_train + tau:]],[x.detach().numpy(), onestep_preds.detach().numpy(),multistep_preds[n_train + tau:].detach().numpy()], 'time','x', legend=['data', '1-step preds', 'multistep preds'],xlim=[1, 1000], figsize=(6, 3))
结果:

预测不理想的原因是:预测误差不断累加。这种现象就像是24小时天气预报,超过24小时以后,精度会迅速下降。
总结
1、时序模型中,当前数据与之前观察到的数据相关
2、自回归模型使用自身过去数据预测未来
3、马尔可夫模型假设当前只跟最近少数数据相关,从而简化模型
4、潜变量模型使用潜变量来概括历史信息
相关文章:

机器学习深度学习——序列模型(NLP启动!)
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——卷积神经网络(LeNet) 📚订阅专栏:机器学习&&深度…...

小白到运维工程师自学之路 第六十四集 (dockerfile构建tomcat、mysql、lnmp、redis镜像)
一、tomcat(更换jdk) mkdir tomcat cd tomcat/ tar xf jdk-8u191-linux-x64.tar.gz tar xf apache-tomcat-8.5.40.tar.gzvim Dockerfile FROM centos:7 MAINTAINER Crushlinux <syh163.com> ADD jdk1.8.0_191 /usr/local/java ENV JAVA_HOME /us…...
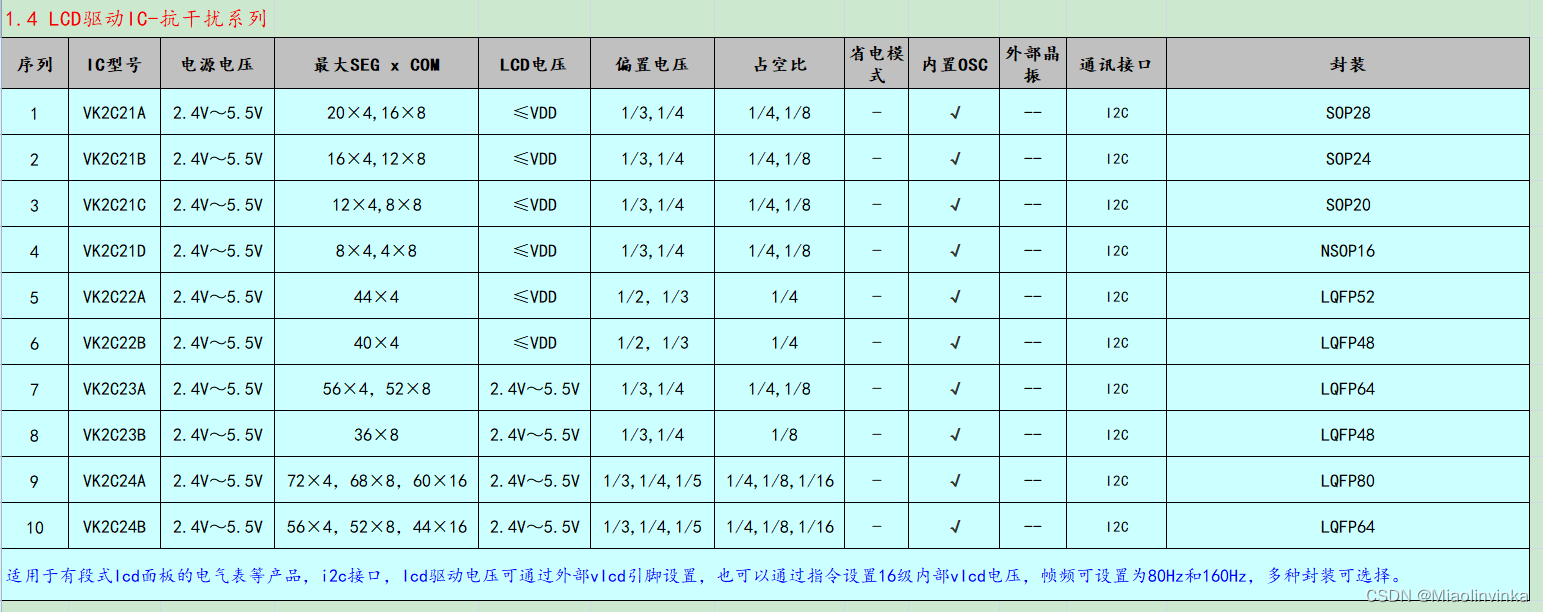
超低功耗水表电器表LCD驱动显示芯片,高抗干扰性能提供LQFP48、LQFP64的封装
VK2C23是一个点阵式存储映射的LCD驱动器,可支持最大224点(56SEGx4COM)或者最大416点(52SEGx8COM)的LCD屏。单片机可通过I2C接口配置显示参数和读写显示数据,也可通过指令进入省电模式。其高抗干扰ÿ…...

SpringBoot3---核心特性---2、Web开发III(模板引擎、国际化、错误处理)
星光下的赶路人star的个人主页 夏天就是吹拂着不可预期的风 文章目录 1、模板引擎1.1 Thymeleaf1.2 基础语法1.3 属性设置1.4 遍历1.5 判断1.6 属性优先级1.7 行内写法1.8 变量选择1.9 模板布局1.10 devtools 2、国家化3、错误处理3.1 默认机制3.2 自定义错误响应3.3 最佳实战 …...
MemFire教程|FastAPI+MemFire Cloud+LangChain开发ChatGPT应用-Part2
基本介绍 上篇文章我们讲解了使用FastAPIMemFire CloudLangChain进行GPT知识库开发的基本原理和关键路径的代码实现。目前完整的实现代码已经上传到了github,感兴趣的可以自己玩一下: https://github.com/MemFire-Cloud/memfirecloud-qa 目前代码主要…...

C# File.Exists与Directory.Exists用法
File.Exists: 用于检查给定文件路径是否存在。如果文件存在,则返回true,否则返回false。 string path“D:\\test\\example.txt” bool exists File.Exists(path); if (exists) {Console.WriteLine("File exists."); } else {Con…...
神经网络修改网络结构如何下手???)
(深度学习,自监督、半监督、无监督!!!)神经网络修改网络结构如何下手???
修改神经网络结构,我们可以根据这个进行添加: 卷积层(Convolutional Layers):标准的卷积层用于提取特征并进行特征映射。 池化层(Pooling Layers):用于减少特征图的空间维度&…...
Codejock Task Panel ActiveX Crack
Codejock Task Panel ActiveX Crack ActiveX COM的Codejock任务面板为Windows开发人员提供了一个复杂的Office任务面板,类似于在Microsoft Office和Windows资源管理器中看到的内容。TaskPanel甚至可以用作Visual Studio风格的工具箱。 功能概述 ActiveX COM的Codejo…...
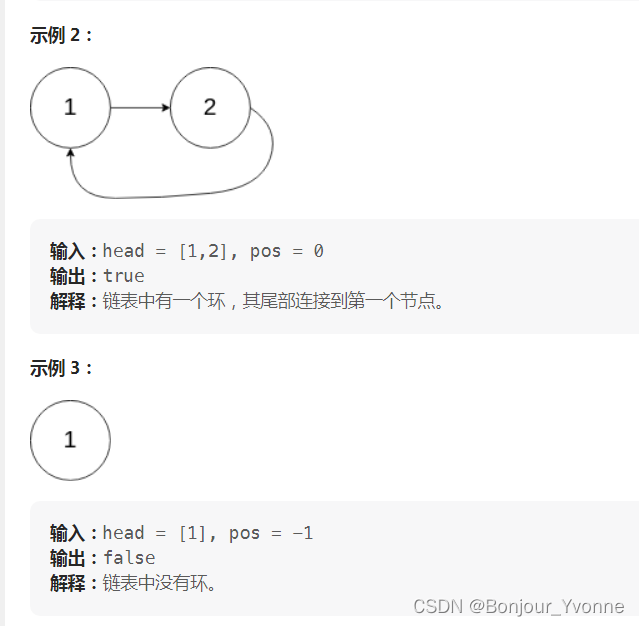
LeetCode 热题 100 JavaScript--141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(…...

文字转语音
键盘获取文字,转化为语音后保存本地 from win32com.client import Dispatch from comtypes.client import CreateObject from comtypes.gen import SpeechLib speakerDispatch(SAPI.SpVoice) speaker.Speak(请输入你想转化的文字) datainput(请输入:)#s…...

让ELK在同一个docker网络下通过名字直接访问
1. docker网络 参考https://blog.csdn.net/lihongbao80/article/details/108019773 https://www.freecodecamp.org/chinese/news/how-to-get-a-docker-container-ip-address-explained-with-examples/ 默认网络有三种,分别是 1、bridge模式,–netbridge(…...

EventBus 开源库学习(一)
一、概念 EventBus是一款在 Android 开发中使用的发布-订阅事件总线框架,基于观察者模式,将事件的接收者和发送者解耦,简化了组件之间的通信,使用简单、效率高、体积小。 一句话:用于Android组件间通信的。 二、原理…...

车载以太网SOME/IP的个人总结
如何实现CAN-SOME/IP通信路由测试 (qq.com) AutoSAR SOMEIP与SOC vsomeip通讯 (qq.com) 利用commonAPI和vSomeip对数据进行序列化 (qq.com) Vector - CANoe - VCDL与SomeIP (qq.com) 使用Wireshark 查看SOMEIP的方法 (qq.com) 基于AutoSAR的车载以太网测试 - SOMEIP之ECU做…...

vue2.29-Vue3跟vue2的区别
1、vue3介绍 更新(和重写)Vue的主要版本时,主要考虑两点因素:首先是新的JavaScript语言特性在主流浏览器中的受支持水平;其次是当前代码库中随时间推移而逐渐暴露出来的一些设计和架构问题。 相较于vue2,vu…...

【深度学习】分类和分割常见损失函数
分类 分类是一种监督机器学习任务,其中训练模型来预测给定输入数据点的类或类别。分类旨在学习从输入特征到特定类或类别的映射。 有不同的分类任务,例如二元分类、多类分类和多标签分类。 二元分类是一项训练模型来预测两个类别之一的任务,…...
Redhat Linux 安装MySQL安装手册
Redhat安装MySQL安装手册 1 下载2 上传服务器、解压并安装3 安装安装过程1:MySQL-shared-5.6.51-1.el7.x86_64.rpm安装过程2:MySQL-shared-compat-5.6.51-1.el7.x86_64.rpm安装过程3:MySQL-server-5.6.51-1.el7.x86_64.rpm安装过程4ÿ…...

题目:2303.计算应缴税款总额
题目来源: leetcode题目,网址:2303. 计算应缴税款总额 - 力扣(LeetCode) 解题思路: 按要求计算即可。注意最多产生 n1 个不同区间内的税款即可。 解题代码: class Solution {public doub…...

Kotlin 1.9.0 发布:带来多项新特性,改进 Multiplatform/Native 支持
新特性 Kotlin 的最新版本引入了许多新的语言特性,包括用于开放范围的…<操作符、扩展正则表达式等。此外,它还改进了 Kotlin Multiplatform 和 Kotlin/Native 支持。 Kotlin 1.9 稳定了与枚举类关联的 entries 属性,它会返回所定义的枚…...

接口测试——认知(一)
目录 引言 环境准备 1. 为什么要进行接口测试 2. 什么是接口 3. 接口测试与功能测试的区别 引言 为什么要做接口自动化测试? 在当前互联网产品迭代频繁的背景下,回归测试的时间越来越少,很难在每个迭代都对所有功能做完整回归。 但接…...

剑指 Offer 10- I. 斐波那契数列
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下: F(0) 0, F(1) 1 F(N) F(N - 1) F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始&am…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...
