数据结构----结构--线性结构--顺序存储--数组
数据结构----结构–线性结构–顺序存储–数组
数组:类型相同,空间连续,长度固定
搜索:
(1)基于索引搜索,时间复杂度O(1)
(2)基于数值搜索:
1.有序的:二分查找
2.无需的:遍历一遍O(n)
增删:
空间不够:扩容 旧数据->新数据 迁移
空间足够:尾增尾删O(1) 其他增删O(n)
关于数组特性的题
第一题
题目:给一个有n个元素的数组,数组内的元素数值范围在0~n-1之间。请检测:数据有无重复出现,如果出现请报错
解决方法:1.暴力 时间复杂度O(n的平方) 空间复杂度 O(1)
2.计数 时间复杂度O(n) 空间复杂度 O(n)
3.排序: 时间复杂度O(看利用哪种排序) 空间复杂度 O(看利用哪种排序)
4.set/map 时间复杂度O(nlog2的n次方) 空间复杂度O(nlog2的n次方)
5.交换 时间复杂度O(n) 空间复杂度 O(1)
这里交换的方法最好 我们用代码实现一下
#include<iostream>
using namespace std;//判断的函数
void PanDuan(int a[],int length) {for (int i = 0; i < length;) {//遍历if (a[i] == i) {//如果下标和数对上了就下一个i++;}else {if (a[i] == a[a[i]]) {//重复cout << "错误" << endl;break;}else {//不重复交换位置int t;t = a[i];a[i] = a[a[i]];a[t] = t;}}
}
int main() {int a[] = { 0,3,2,4,1 };//定义一个数组,进行测试PanDuan(a,(sizeof(a)/sizeof(a[0])));//进入判断的函数return 0;
}
第二题
题目:一组数据,其中有一个元素只出现一次,其他元素均出现两次,请找出只出现一次的元素
解决方法:1.暴力 时间复杂度O(n的平方) 空间复杂度 O(1)
2.计数 (哈希表,map)
哈希表 时间复杂度O(n) 空间复杂度 O(n)
map 时间复杂度O(nlog2的n次方) 空间复杂度 O(n)
3.异或 时间复杂度O(n) 空间复杂度 O(1)
更改题目为:一组数据,其中有两个元素只出现一次,其他元素均出现两次,请找出只出现一次的元素
最优解决方法: 第一步:整体异或
第二步:找到非0位
第三步:根据非0位进行分组,分为两组
第四步:各组异或 就得到了只出现一次的这两个元素
用代码进行实现,如下
#include <iostream>
using namespace std;void Find(int arr[]){int res1 = 0;for (int i : arr) {//全部异或一遍 获得两个只出现一次元素的异或的结果res1 ^= i;}unsigned int res2 = 1;//从右到左找到二进制上第一个为1的while (1) {//与1进行位于if (res1 & res2) {break;}res2 = res2 << 1;}int result1 = 0;int result2 = 0;for (int i : arr) {//遍历分类并对两组数进行异或得到结果if (res2 & i) {result1 ^= i;}else {result2 ^= i;}}cout << result1 << " " << result2 << endl;
}
int main() {int nums[] = { 1,5,5,4,4,3 };//这里是测试样例Find(nums);return 0;
}
相关文章:

数据结构----结构--线性结构--顺序存储--数组
数据结构----结构–线性结构–顺序存储–数组 数组:类型相同,空间连续,长度固定 搜索: (1)基于索引搜索,时间复杂度O(1) (2)基于数值搜索: 1.有序的&…...

docker 启动kitex 的opentelemetry
https://github.com/cloudwego/kitex-examples/blob/main/opentelemetry/docker-compose.yaml 下载两个yaml文件:docker-compose.yaml otel-collector-config.yaml 在该目录下执行 docker-compose up -d...
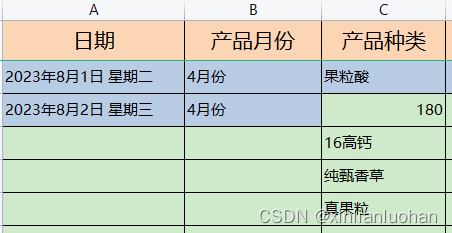
Excel中——日期列后添加星期
需求:在日期列中添加星期几? 第一步:打开需要添加星期的Excel文件,在日期后面添加日期 第二步:选择日期列,点击鼠标右键,在下拉列表中,选择“设置单元格格式” 第三步: 在…...
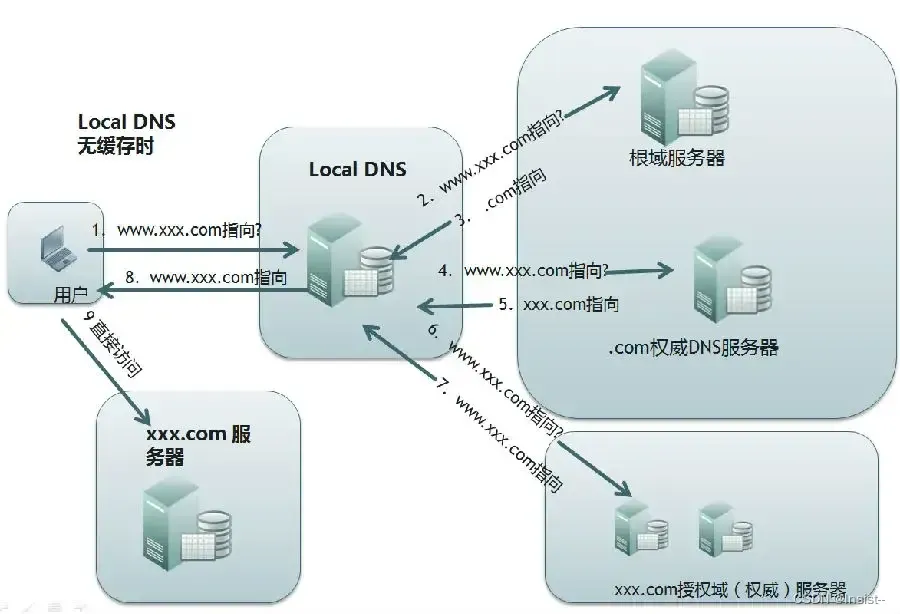
谈谈DNS是什么?它的作用以及工作流程
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 目录 一、DNS是什么? 二、DNS的作用 三、DNS查询流程 1、查看浏览器缓存 2、查看系统缓存 3、查看路由器缓存 4、查看ISP …...

Qt小项目贪吃蛇实线,主要掌握定时器、信号与槽、按键事件、绘制事件、坐标运算、随机数生成等
Qt小项目贪吃蛇实线,主要掌握定时器、信号与槽、按键事件、绘制事件、坐标运算、随机数生成等 Qt 贪吃蛇演示QWidget 绘制界面项目源文件 注释清晰widget.hwidget.cpp 拓展QTimerQKeyEventQRectFQPointFQPainterQIcon Qt 贪吃蛇演示 QWidget 绘制界面 项目源文件 注…...

使用HTTP隧道时如何应对目标网站的反爬虫监测?
在进行网络抓取时,我们常常会遇到目标网站对反爬虫的监测和封禁。为了规避这些风险,使用代理IP成为一种常见的方法。然而,如何应对目标网站的反爬虫监测,既能保证数据的稳定性,又能确保抓取过程的安全性呢?…...
怎么样通过Bootstrap已经编译好(压缩好)的源码去查看符合阅读习惯的源码【通过Source Map(源映射)文件实现】
阅读本篇博文前,建议大家先看看下面这篇博文: https://blog.csdn.net/wenhao_ir/article/details/132089650 Bootstrap经编译(压缩)后的源码百度网盘下载地址: https://pan.baidu.com/s/14BM9gpC3K-LKxhyLGh4J9Q?pwdm02m Bootstrap未经编译…...
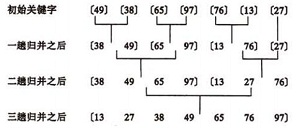
【排序算法】python之冒泡,选择,插入,快速,归并
参考资料: 《Python实现5大排序算法》《六大排序算法:插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序》 --代码似乎是C语言 ———————— 本文介绍5种常见的排序算法和基于Python实现: 冒泡排序(Bubble Sort&am…...

UML—用例图的那些事
目录 背景: 1.用例图的发展史 过程: 1.用例图中的元素和关系 2.应用中的例子 总结: 背景: 1.用例图的发展史 用例图是一种常用的软件工程工具,用于描述系统的功能需求和用户与系统的交互。它在软件开发过程中起到了重要的作用,并且经历了…...
)
迷宫出口问题求解(DFS)
题面 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 nn 的格点组成,每个格点只有 22 种状态, 00 和 11,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只能移动到东南西北…...

基础算法模板
数据结构 单链表的插入删除 const int N=1e6+10; int head,e[N],ne[N],idx; //head 存储头节点的下标 //idx 存储当前已经用到的那个点 void init() {head=-1;idx=0; } void add_to_head(int x)//插入头节点操作 {e[idx]=x;ne[idx]=head;head=idx;idx++; } void add(int k)/…...

react Ref 的基本使用
类组件中使用ref 在类组件中,你可以使用createRef来创建一个ref,并将它附加到DOM元素或类组件实例上。使用ref允许你在类组件中访问和操作特定的DOM元素或类组件实例。 下面是在类组件中使用ref的步骤: 引入React和createRef: …...
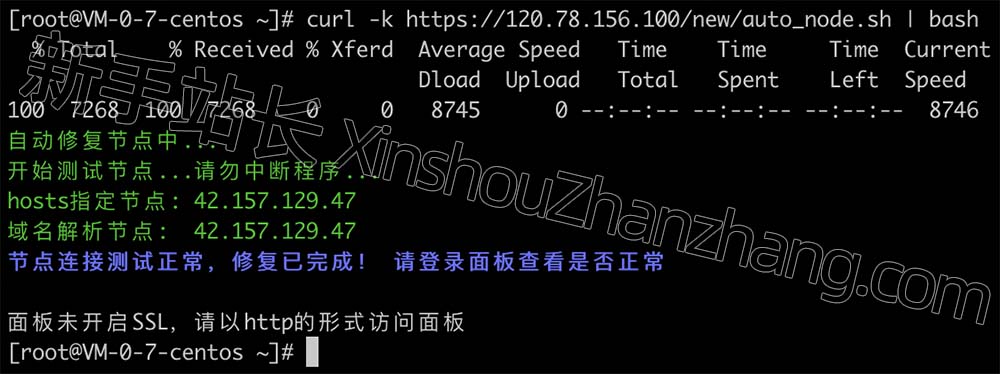
宝塔面板点击SSL闪退打不开怎么解决?
宝塔Linux面板点击SSL证书闪退如何解决?旧版本的宝塔Linux面板确实存在这种情况,如何解决?升级你的宝塔Linux面板即可。新手站长分享宝塔面板SSL闪退的解决方法: 宝塔面板点击SSL证书闪退解决方法 问题:宝塔Linux面板…...

如何将安卓 Gradle 模块打包发布到本地 Maven 仓库
文章目录 具体流程 笔者的运行环境: Android Studio Flamingo | 2022.2.1 Android SDK 33 Gradle 8.0.1 JDK 17 Android 的 Gradle 项目与一般的 Gradle 项目是不同的,因此对将 Gradle 模块打包发布到本地 Maven 仓库来说,对普通 Gradle …...
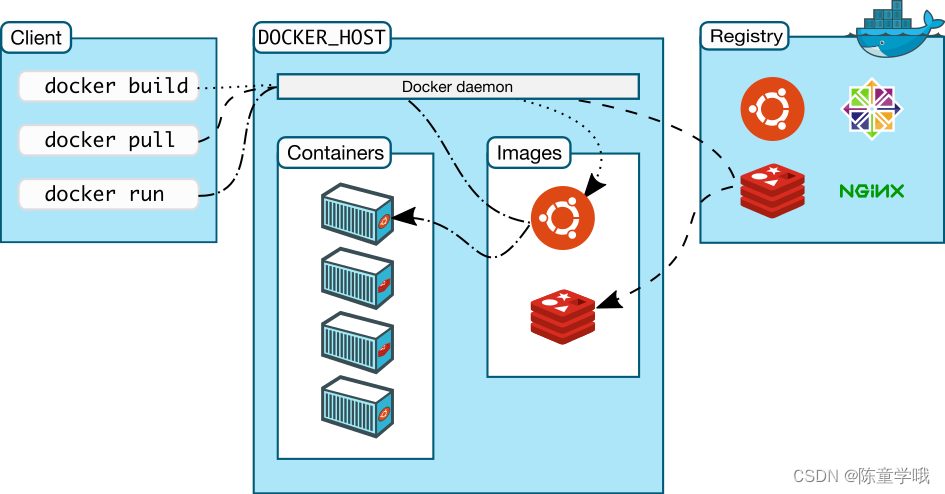
【Docker】Docker比虚拟机快的原因、ubuntu容器、镜像的分层概念和私有库的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...

java.lang.IllegalArgumentException: Invalid character found in methodname
postman请求异常:java.lang.IllegalArgumentException: Invalid character found in method name. HTTP method names must be tokens...
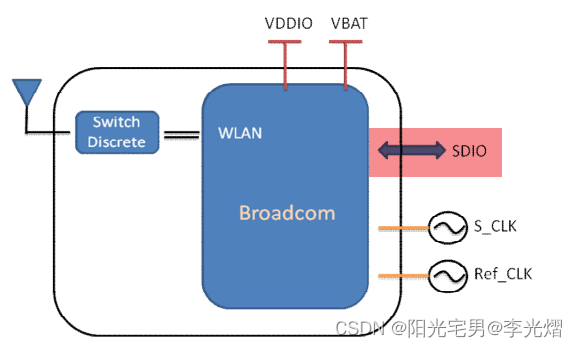
【PCB专题】Allegro高速电路Xnet网络等长约束——SDIO信号为例
高速PCB板布线过程中,经常遇到等长设置问题,例如DDR的一组数据线和地址线等。但是由于数据线和地址线中间有一个电阻(或排阻),这种情况下设置等长就要引入Xnet的概念,通过设置Xnet的等长来确保数据线和地址线的等长。 由无源、分立器件(电阻、电容、电感)连接起来的几段…...
leetcode每日一练-第278题-第一个错误的版本
一、思路 二分查找——因为它可以快速地将版本范围缩小一半,从而更快地找到第一个坏版本。 二、解题方法 维护一个左边界 left 和一个右边界 right,在每一步循环中,我们计算中间版本 mid,然后检查它是否是坏版本。如果是坏版本…...
)
最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树 最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。 换句话说,最小生成树是原图中的一个子图&#…...

4、数据清洗
4、数据清洗 前面我们处理的数据实际上都是已经被处理好的规整数据,但是在大数据整个生产过程中,需要先对数据进行数据清洗,将杂乱无章的数据整理为符合后面处理要求的规整数据。 数据去重 1.删除重复数据groupby().count():可以…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
