基础算法模板
数据结构
单链表的插入删除
const int N=1e6+10;
int head,e[N],ne[N],idx;
//head 存储头节点的下标
//idx 存储当前已经用到的那个点
void init()
{head=-1;idx=0;
}
void add_to_head(int x)//插入头节点操作
{e[idx]=x;ne[idx]=head;head=idx;idx++;
}
void add(int k)//将x插入到下表是k的点后面
{e[idx]=k;ne[idx]=ne[k];ne[k]=idx;idx++;
}//删除操作
//将下标k后面的一个点删掉
void remove(int x)
{ne[k]=ne[ne[k]];
}
模拟栈
const int N=100010;
int n,m;
int stv[N],tt;
int main()
{scanf("%d",&m);while(m--){string op;int x;cin>>op;if(op=="push"){scanf("%d",&x);stv[++tt]=x;}else if(op=="pop")tt--;else if(op=="empty"){if(tt==0)printf("YES\n");else printf("NO\n");}else printf("%d\n",stv[tt]);}return 0;
}模拟队列
const int N = 100010;int m;
int q[N], hh, tt = -1;int main()
{cin >> m;while (m -- ){string op;int x;cin >> op;if (op == "push"){cin >> x;q[ ++ tt] = x;}else if (op == "pop") hh ++ ;else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;else cout << q[hh] << endl;}return 0;
}trie字符串统计
#include<iostream>
using namespace std;
const int N=1e6+10;
int son[N][26],cnt[N],idx;
char str[N];
void insert(char str[])
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';if(!son[p][u])son[p][u]=++idx;p=son[p][u];}cnt[p]++;
}
int query(char str[])
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';if(!son[p][u])return 0;else p=son[p][u];}return cnt[p];
}
int main()
{int n;cin>>n;while(n--){char op[2];cin>>op>>str;if(*op=='I')insert(str);else printf("%d\n",query(str));}return 0;
}
并查集
1.将两个集合合并
2.询问两个元素是否在一个集合中
基本原理:每个集合用一个树来表示,树根的编号就是在整个集合的编号。每个节点存储它的父节点,p[x]表示x的父节点
问题一:如何判断树根if(p[x]==x)
问题二:如何求x的集合编号while(p[x]!=x)x=p[x];
问题三:如何合并两个集合:p[x]是x的集合编号p[y]是y的集合编号,p[x]=y;
优化 路径压缩
#include<iostream>
using namespace std;
const int N=100100;
int p[N];
int n,m;
int find(int x)//返回X的祖宗节点+路径压缩
{if(p[x]!=x)p[x]=find(p[x]);return p[x];
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){p[i]=i;}while(m--){char op[2];int a,b;scanf("%s%d%d",op,&a,&b);if(op[0]=='M')p[find(a)]=find(b);//a的祖宗节点插入到B的父节点else{if(find(a)==find(b))puts("Yes");else puts("No");}}
}
堆
1.插入一个数
2.求集合的最小值
3.删除最小值
4.删除任意一个元素
5.修改任意一个元素
堆的一个基本结构:一棵二叉树(完全(除了最后一层节点,上面所有节点都是满的,最后一层从左到右排列))
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6+10;
int n,m;
int h[N],cnt;
void down(int u)
{int t=u;if(u*2<=cnt && h[u*2]<h[t])t=u*2;if(u*2+1<=cnt&&h[u*2+1]<h[t])t=u*2+1;if(u!=t){swap(h[u],h[t]);down(t);}
}
void up(int u)
{while(u/2&&h[u/2]>h[u]){swap(h[u],h[u/2]);u/=2;}
}
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>h[i];cnt=n;for(int i=n/2;i>=1;i--){down(i);}while(m--){printf("%d ",h[1]);h[1]=h[cnt];cnt--;down(1);}return 0;
}
hash表 哈希表
存储结构和字符串哈希的方式
存储结构:开放寻值法 拉链法
作用:把一个庞大的空间映射到比较小的空间
(1)拉链法,开一个一维数组
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100003;
int h[N],e[N],ne[N],idx;
void insert(int x)
{int k=(x%N+N)%N;e[idx]=x;ne[idx]=h[k];h[k]=idx++;}
bool find(int x)
{int k=(x%N+N)%N;for(int i=h[k];i!=-1;i=ne[i])if(e[i]==x)return true;return false;
}
int main()
{int n;cin>>n;memset(h, -1, sizeof h);while(n--){char op[2];int x;scanf("%s%d",op,&x);if(*op=='I')insert(x);else {if(find(x))printf("Yes\n");else printf("No\n");}}return 0;
}
2.开放寻值法
#include <cstring>
#include <iostream>using namespace std;const int N = 200003, null = 0x3f3f3f3f;int h[N];int find(int x)
{int t = (x % N + N) % N;while (h[t] != null && h[t] != x){t ++ ;if (t == N) t = 0;}return t;
}int main()
{memset(h, 0x3f, sizeof h);int n;scanf("%d", &n);while (n -- ){char op[2];int x;scanf("%s%d", op, &x);if (*op == 'I') h[find(x)] = x;else{if (h[find(x)] == null) puts("No");else puts("Yes");}}return 0;
}
3.字符串哈希
#include <iostream>
#include <algorithm>using namespace std;typedef unsigned long long ULL;const int N = 100010, P = 131;int n, m;
char str[N];
ULL h[N], p[N];ULL get(int l, int r)
{return h[r] - h[l - 1] * p[r - l + 1];
}int main()
{scanf("%d%d", &n, &m);scanf("%s", str + 1);p[0] = 1;for (int i = 1; i <= n; i ++ ){h[i] = h[i - 1] * P + str[i];p[i] = p[i - 1] * P;}while (m -- ){int l1, r1, l2, r2;scanf("%d%d%d%d", &l1, &r1, &l2, &r2);if (get(l1, r1) == get(l2, r2)) puts("Yes");else puts("No");}return 0;
}C++STL
vector, 变长数组,倍增的思想size() 返回元素个数empty() 返回是否为空clear() 清空 front()/back()push_back()/pop_back()begin()/end()[] 支持比较运算,按字典序pair<int, int>first, 第一个元素second, 第二个元素支持比相关文章:

基础算法模板
数据结构 单链表的插入删除 const int N=1e6+10; int head,e[N],ne[N],idx; //head 存储头节点的下标 //idx 存储当前已经用到的那个点 void init() {head=-1;idx=0; } void add_to_head(int x)//插入头节点操作 {e[idx]=x;ne[idx]=head;head=idx;idx++; } void add(int k)/…...

react Ref 的基本使用
类组件中使用ref 在类组件中,你可以使用createRef来创建一个ref,并将它附加到DOM元素或类组件实例上。使用ref允许你在类组件中访问和操作特定的DOM元素或类组件实例。 下面是在类组件中使用ref的步骤: 引入React和createRef: …...
宝塔面板点击SSL闪退打不开怎么解决?
宝塔Linux面板点击SSL证书闪退如何解决?旧版本的宝塔Linux面板确实存在这种情况,如何解决?升级你的宝塔Linux面板即可。新手站长分享宝塔面板SSL闪退的解决方法: 宝塔面板点击SSL证书闪退解决方法 问题:宝塔Linux面板…...

如何将安卓 Gradle 模块打包发布到本地 Maven 仓库
文章目录 具体流程 笔者的运行环境: Android Studio Flamingo | 2022.2.1 Android SDK 33 Gradle 8.0.1 JDK 17 Android 的 Gradle 项目与一般的 Gradle 项目是不同的,因此对将 Gradle 模块打包发布到本地 Maven 仓库来说,对普通 Gradle …...
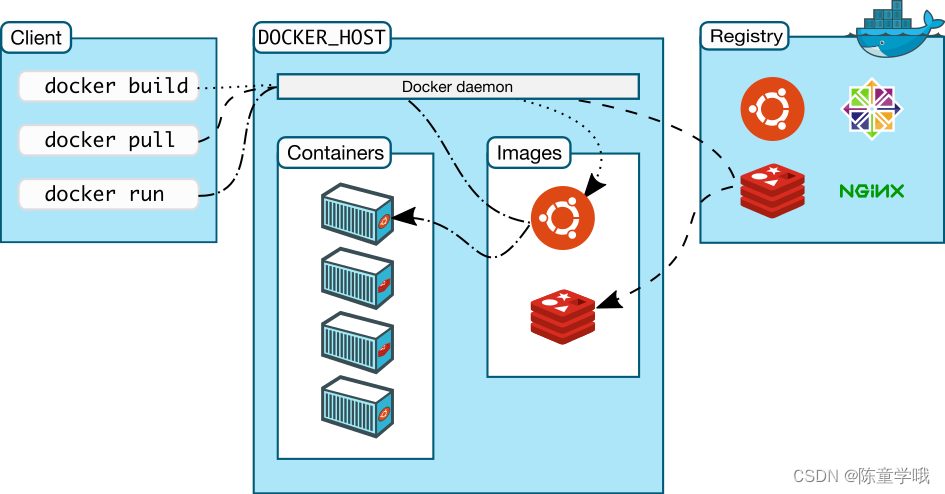
【Docker】Docker比虚拟机快的原因、ubuntu容器、镜像的分层概念和私有库的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...

java.lang.IllegalArgumentException: Invalid character found in methodname
postman请求异常:java.lang.IllegalArgumentException: Invalid character found in method name. HTTP method names must be tokens...
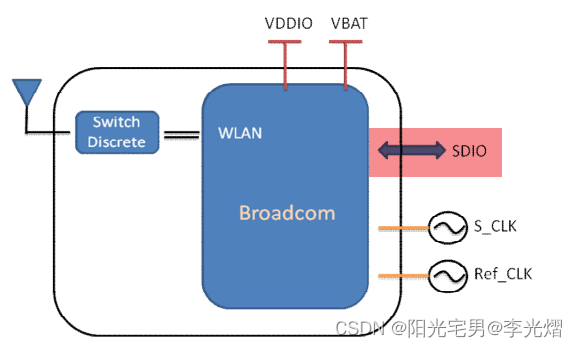
【PCB专题】Allegro高速电路Xnet网络等长约束——SDIO信号为例
高速PCB板布线过程中,经常遇到等长设置问题,例如DDR的一组数据线和地址线等。但是由于数据线和地址线中间有一个电阻(或排阻),这种情况下设置等长就要引入Xnet的概念,通过设置Xnet的等长来确保数据线和地址线的等长。 由无源、分立器件(电阻、电容、电感)连接起来的几段…...
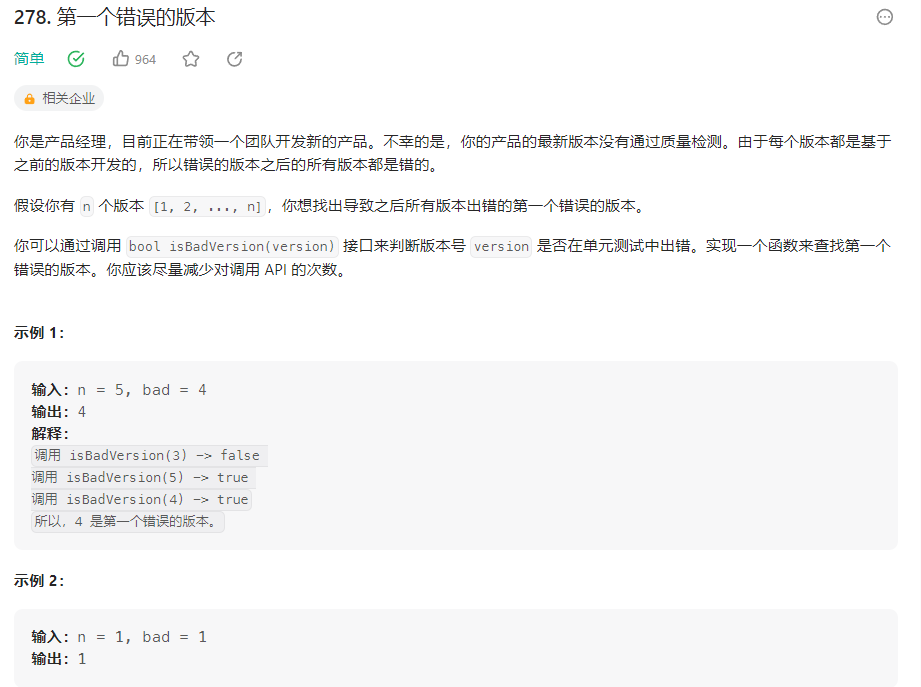
leetcode每日一练-第278题-第一个错误的版本
一、思路 二分查找——因为它可以快速地将版本范围缩小一半,从而更快地找到第一个坏版本。 二、解题方法 维护一个左边界 left 和一个右边界 right,在每一步循环中,我们计算中间版本 mid,然后检查它是否是坏版本。如果是坏版本…...
)
最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树 最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。 换句话说,最小生成树是原图中的一个子图&#…...

4、数据清洗
4、数据清洗 前面我们处理的数据实际上都是已经被处理好的规整数据,但是在大数据整个生产过程中,需要先对数据进行数据清洗,将杂乱无章的数据整理为符合后面处理要求的规整数据。 数据去重 1.删除重复数据groupby().count():可以…...

Python-OpenCV 图像的基础操作
图像的基础操作 获取图像的像素值并修改获取图像的属性信息图像的ROI区域图像通道的拆分及合并图像扩边填充图像上的算术运算图像的加法图像的混合图像的位运算 获取图像的像素值并修改 首先读入一副图像: import numpy as np import cv2# 1.获取并修改像素值 # 读…...

test111
step3:多线程task 首先,实现两个UserService和AsyncUserService两个服务接口: package com.example.demospringboot.service;public interface UserService {void checkUserStatus(); }package com.example.demospringboot.service.impl;im…...
17. Spring 事务
目录 1. 事务定义 2. MySQL 中的事务使用 3. 没有事务时的插入 4. Spring 编程式事务 5. Spring 声明式事务 5.1 Transactional 作用范围 5.2 Transactional 参数说明 5.3 Transactional 工作原理 1. 事务定义 将⼀组操作封装成一个执行单元(封装到一起…...

【C# 基础精讲】运算符和表达式
在C#编程中,运算符和表达式是构建复杂逻辑的关键元素。运算符用于执行各种数学、逻辑和其他操作,而表达式则由运算符、变量、常量和函数组成,用于生成计算结果。本文将详细介绍C#中常见的运算符和表达式的概念,以及它们在程序中的…...

【搜索】DFS连通性模型
算法提高课笔记 目录 迷宫题意思路代码 红与黑题意思路代码 DFS 的搜索分为两大部分: 内部搜索:一个图中从一个点搜到另一个点外部搜索:从一张图(状态)搜到另一张图(状态) 在第一个部分里是图…...

项目优化后续 ,手撸一个精简版VUE项目框架!
之前说过项目之前用的vben框架,在优化完性能后打包效果由原来的纯代码96M变成了56M,后续来啦,通过更换框架,代码压缩到了36M撒花~ 现在就来详细说说是怎么手撸一个框架的! 方案: 搭建一套 vite vue3 a…...
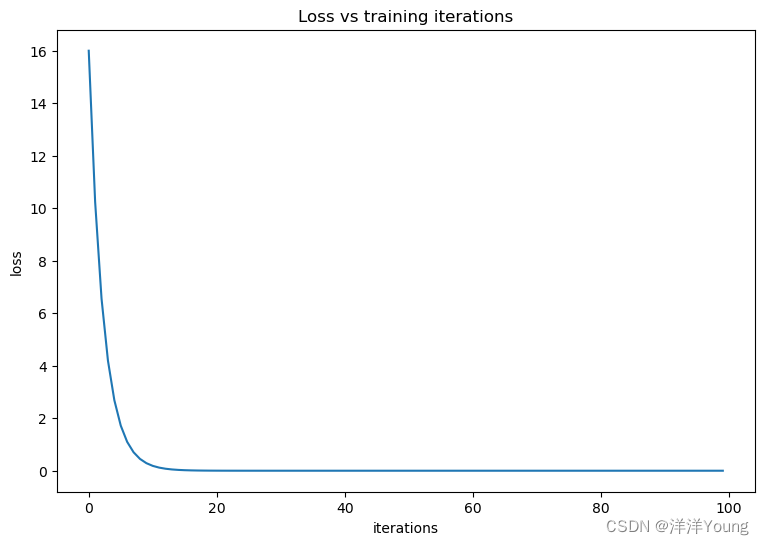
【深度学习笔记】TensorFlow 基础
在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。…...

面试题-springcloud中的负载均衡是如何实现的?
一句话导读 Springcloud中的负载均衡是通过Ribbon实现的,自带有很多负载均衡策略,如:包括轮询(Round Robin)、随机(Random)、加权轮询(Weighted Round Robin)、加权随机&…...

flink的ProcessWindowFunction函数的三种状态
背景 在处理窗口函数时,ProcessWindowFunction处理函数可以定义三个状态: 富函数getRuntimeContext.getState, 每个key每个窗口的状态context.windowState(),每个key的状态context.globalState,那么这几个状态之间有什么关系呢? …...
day50-springboot+ajax分页
分页依赖: <dependency> <groupId>com.github.pagehelper</groupId> <artifactId>pagehelper-spring-boot-starter</artifactId> <version>1.0.0</version> </dependency> 配置: …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

day51 python CBAM注意力
目录 一、CBAM 模块简介 二、CBAM 模块的实现 (一)通道注意力模块 (二)空间注意力模块 (三)CBAM 模块的组合 三、CBAM 模块的特性 四、CBAM 模块在 CNN 中的应用 一、CBAM 模块简介 在之前的探索中…...
