【排序算法】python之冒泡,选择,插入,快速,归并
参考资料:
- 《Python实现5大排序算法》
- 《六大排序算法:插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序》 --代码似乎是C语言
————————
本文介绍5种常见的排序算法和基于Python实现:
冒泡排序(Bubble Sort):通过不断交换相邻元素,将较大的元素逐渐“冒泡”到数组的尾部,较小的元素逐渐沉到数组的头部。
选择排序(Selection Sort):每次从未排序的部分中选择最小(或最大)的元素,然后放到已排序部分的末尾(或开头)。
插入排序(Insertion Sort):将数组分为已排序和未排序两部分,逐个将未排序元素插入到已排序部分的适当位置,使其保持有序。
快速排序(Quick Sort):通过递归地选择一个基准元素,并将数组划分为小于基准和大于基准的两部分,然后对两部分继续进行快速排序。
归并排序(Merge Sort):将数组拆分成两个子数组,对每个子数组进行排序,然后再将两个有序子数组合并成一个有序数组。
不同的排序算法在时间复杂度、空间复杂度以及稳定性等方面有所不同,选择适合具体情况的排序算法可以提高排序效率。
一、冒泡排序
冒泡排序是一种简单的排序算法,它的思想是重复地走访过要排序的元素列,依次比较相邻的两个元素,如果它们的顺序错误就交换它们,直到没有任何再需要交换的元素,排序完成。

案例
我们以升序为实例。【34,,64,,11,,12,,22,,25,,90】长度为7.
第一次循环,要判断交换n-1次=6.两两交换,要将最大值90沉到末尾。结果为:【34,,11,,12,,22,,25,,64,,90】

第二次循环,要判断n-2次=5.两两交换,要将次最大值64沉到尾部(90之前)。结果为:
【11,,12,,22,,25,,34,,64,,90】
第三次循环,要判断n-3次=4. 值得注意的是,在这次循环中,没有一次交换行为。
第四次循环,要判断n-4次=3.值得注意的是,在这次循环中,没有一次交换行为。
第五次循环,要判断n-5次=2.值得注意的是,在这次循环中,没有一次交换行为。
第六次循环,要判断n-6次=1.值得注意的是,在这次循环中,没有一次交换行为。
因此,设置一个“标志位”,用于优化。若某次循环中没有交换元素,说明数组已经有序,可以提前结束排序。即在第三次循环中,判断没有交换,则可以提前结束优化了。
1.1 代码
def bubble_sort(arr):n = len(arr)for i in range(n - 1):# 标志位,用于优化:若某次循环中没有交换元素,说明数组已经有序,可以提前结束排序swapped = Falsefor j in range(n - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]swapped = Trueif not swapped:break测试
# 使用示例
arr = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(arr)
print(arr) # 输出:[11, 12, 22, 25, 34, 64, 90]在冒泡排序中,外层循环控制需要比较的次数,内层循环实际进行相邻元素的比较和交换。通过标志位swapped的引入,可以优化冒泡排序,当某次循环没有发生交换时,说明数组已经有序,可以提前结束排序。这样在数组近乎有序的情况下,冒泡排序的性能会有所提升。
改进
“swapped”是优化的循环次数,提前截止循环。当序列的长度足够大的时候,在循环的某次的内部是否可以提前截止交换呢?
【22,,12,,11,25, 34,,64 ,90】

假设,如果我们用last_swap_index记录当前轮次最后交换的位置。在下一轮的循环的时候,提前结束判断交换。则在每个循环轮次中节省很多判断和步骤。因此,优化后的代码为:
1.2 优化后的代码
def bubble_sort(arr):n = len(arr)for i in range(n - 1):swapped = False# 记录当前轮循环最后一次交换的位置,初始值为未排序部分的末尾last_swap_index = n - 1for j in range(n - i - 1):if arr[j] > arr[j + 1]:arr[j], arr[j + 1] = arr[j + 1], arr[j]swapped = Truelast_swap_index = j # 更新最后一次交换的位置if not swapped:break# 更新下一轮未排序部分的边界n = last_swap_index + 1
1.3 复杂度
时间复杂度:最坏情况:O(N^2)
最好情况:O(N)
空间复杂度:O(1)
二、选择排序
选择排序(Selection Sort)是一种简单直观的排序算法,其思想是在未排序部分找到最小(或最大)元素,然后与未排序部分的第一个元素交换位置。重复这个过程直到所有元素都有序。

2.1 代码
def selection_sort(arr):n = len(arr)for i in range(n - 1):# 假设当前未排序部分的第一个元素是最小的min_idx = i# 在未排序部分中找到最小元素的索引for j in range(i + 1, n):if arr[j] < arr[min_idx]:min_idx = j# 将找到的最小元素与未排序部分的第一个元素交换位置arr[i], arr[min_idx] = arr[min_idx], arr[i]
测试
arr = [64, 34, 25, 12, 22, 11, 90]
selection_sort(arr)
print(arr) # 输出:[11, 12, 22, 25, 34, 64, 90]
在选择排序中,外层循环控制需要排序的次数,内层循环在未排序部分中找到最小元素的索引。然后将找到的最小元素与未排序部分的第一个元素交换位置。这样每一轮循环会将未排序部分的最小元素放到已排序部分的末尾,从而实现排序。选择排序的时间复杂度是O(n^2),它是一个不稳定的排序算法。
改进
换个角度看,外层循环指示了已排序部分的末尾,要求所有的元素都必须经历排序,因此,外层循环是不可能像冒泡排序一样提前截止的。在每次循环的内部选择最小元素的时候,我们也必须在所有未排序的元素中选择,也不可以提前截止。因此,我们只能将优化的注意力放在“交换”上。
例如:【11,,12,,22,,25,,34,,90,,64】
第一次循环,位置arr[0], 选择最小的arr[0]–>交换
第二次循环,位置arr[1], 选择最小的arr[1]–>交换
第二次循环,位置arr[2], 选择最小的arr[2]–>交换
。。。
可以看到,出现了很多不必要的交换。因此,添加一个判断因素,从而停止交换。—提醒的是,计算机做判断的消耗的运行时间远远小于数组的位置交换所消耗的时间。
2.2 优化的代码
def selection_sort(arr):n = len(arr)for i in range(n - 1):min_idx = ifor j in range(i + 1, n):if arr[j] < arr[min_idx]:min_idx = j# 如果最小元素的索引不是当前的第一个元素,才进行交换if min_idx != i:arr[i], arr[min_idx] = arr[min_idx], arr[i]
通过增加一个条件判断,只有当最小元素的索引不等于当前的第一个元素的索引时,才进行交换操作。这样就可以减少不必要的交换,进而优化选择排序的性能。这个优化对于已经近乎有序的数组尤为有效,因为这些情况下交换次数较少。尽管选择排序的时间复杂度仍然是O(n^2),但这样的优化可以提高它的效率。
2.3 复杂度
时间复杂度:最坏情况:O(N^2)
最好情况:O(N^2)
空间复杂度:O(1)
三、插入排序
插入排序(Insertion Sort)是一种简单的排序算法,其基本思想是将数组分为已排序和未排序两个部分,逐个将未排序元素插入到已排序部分的适当位置,使其保持有序。

在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。

案例

3.1 代码
def insertion_sort(arr):n = len(arr)for i in range(1, n):key = arr[i] # 当前要插入的元素j = i - 1 # 已排序部分的最后一个元素的索引# 逐个将已排序部分中比key大的元素后移,为key找到合适的插入位置while j >= 0 and key < arr[j]:arr[j + 1] = arr[j]j -= 1# 插入key到合适的位置arr[j + 1] = key
在插入排序中,外层循环控制需要插入的次数,从第2个元素开始(索引为1),依次向已排序部分插入未排序部分的元素。内层循环用于将已排序部分中比当前元素key大的元素后移,为key找到合适的插入位置。最后,将key插入到合适的位置,完成一次插入操作。
改进
在外层循环控制的插入次数,所有的元素都要被插入,因此无法提前截止。内层循环控制的是插入位置,一一倒序比较插入的位置是否合适。为了更快的找到插入位置,可以使用二分法判断插入位置。
3.2 优化的代码
def insertion_sort(arr):n = len(arr)for i in range(1, n):key = arr[i]left, right = 0, i - 1# 使用二分查找找到key应该插入的位置while left <= right:mid = (left + right) // 2if arr[mid] > key:right = mid - 1else:left = mid + 1# 将已排序部分中大于key的元素都后移一位for j in range(i, left, -1):arr[j] = arr[j - 1]arr[left] = key# 使用示例
arr = [64, 34, 25, 12, 22, 11, 90]
insertion_sort(arr)
print(arr) # 输出:[11, 12, 22, 25, 34, 64, 90]
3.3 复杂度
时间复杂度
最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序
最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
四、快速排序
快速排序(Quick Sort)是一种高效的排序算法,它使用分治法来对数组进行排序。快速排序的基本思想是选择一个基准元素(pivot),然后将数组中小于等于基准的元素放在左边,大于基准的元素放在右边,然后分别对左右两部分递归地进行快速排序,直到整个数组有序为止。
案例
以【34,,25,,11,,22,,12,,64,,90】为例。
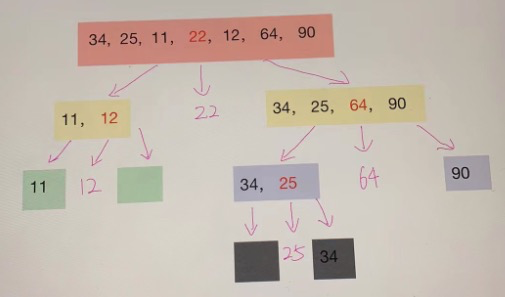
4.1 代码
def quick_sort(arr):if len(arr) <= 1:return arrpivot = arr[len(arr) // 2] # 选择中间的元素作为基准left = [x for x in arr if x < pivot]middle = [x for x in arr if x == pivot]right = [x for x in arr if x > pivot]return quick_sort(left) + middle + quick_sort(right)
改进
在优化快速排序的代码中,主要关注减少递归调用的次数和减少额外空间的使用。以下是针对这两方面的优化方法:
- 优化递归调用次数:对于小规模的子数组,可以切换到其他排序算法,例如插入排序。这是因为在小规模数据下,插入排序的常数项较小,比快速排序的递归开销更小。
- 减少额外空间的使用:原始的快速排序需要额外的数组空间用于存放左右子数组,但我们可以通过就地分区的方式来减少空间使用。
或者说是用挖坑法 减少额外空间的使用。注意,在减少空间使用的的快速排序算法有很多,下面这个动态图比较形象,所以放在这里的。这与我们 下面使用的partition的代码不一致。

4.2 优化的代码
对于小规模的子数组,切换到插入排序
def insertion_sort(arr, low, high):for i in range(low + 1, high + 1):key = arr[i]j = i - 1while j >= low and key < arr[j]:arr[j + 1] = arr[j]j -= 1arr[j + 1] = keydef partition(arr, low, high):pivot = arr[high] ##注意这里的坑位与前面的动态图相反,选择的是最后一个位置而不是首位置i = low - 1for j in range(low, high):if arr[j] <= pivot:i += 1arr[i], arr[j] = arr[j], arr[i]arr[i + 1], arr[high] = arr[high], arr[i + 1]return i + 1def quick_sort(arr, low, high):if low < high:# 对于小规模的子数组,切换到插入排序if high - low + 1 <= 10:insertion_sort(arr, low, high)else:pivot_index = partition(arr, low, high)quick_sort(arr, low, pivot_index - 1)quick_sort(arr, pivot_index + 1, high)
测试
arr = [64, 34, 25, 12, 22, 11, 90]
quick_sort(arr, 0, len(arr) - 1)
print(arr) # 输出:[11, 12, 22, 25, 34, 64, 90]
在优化后的代码中,我们引入了insertion_sort函数用于对小规模子数组进行插入排序。当子数组大小不超过10个元素时,切换到插入排序。同时,在quick_sort函数中采用就地分区的方法,减少了额外的空间使用。
这些优化方法可以提高快速排序在小规模数据和近乎有序数组的性能。但需要注意的是,优化的效果也依赖于具体的数据情况
4.3 案例讲解–partition的应用
以【72,,64,,34,,25,,12,,22,,90,,17,,45,,58】为例。当子数组规模小于3的时候,切换到“插入排序”。以其中一轮为例。

递归调用的树状图

五、 归并算法
归并排序(Merge Sort)是一种高效稳定的排序算法,它使用分治法将数组分为两个子数组,递归地对子数组进行排序,然后将排好序的子数组合并成一个有序数组。
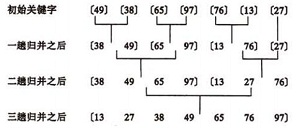
5.1 代码
def merge_sort(arr):if len(arr) <= 1:return arr# 将数组一分为二mid = len(arr) // 2left = arr[:mid]right = arr[mid:]# 递归对左右两部分进行归并排序left = merge_sort(left)right = merge_sort(right)# 合并已排序的左右两部分return merge(left, right)def merge(left, right):merged = []left_idx, right_idx = 0, 0while left_idx < len(left) and right_idx < len(right):if left[left_idx] < right[right_idx]:merged.append(left[left_idx])left_idx += 1else:merged.append(right[right_idx])right_idx += 1# 将剩余的元素加入合并后的数组merged.extend(left[left_idx:])merged.extend(right[right_idx:])return merged相关文章:

【排序算法】python之冒泡,选择,插入,快速,归并
参考资料: 《Python实现5大排序算法》《六大排序算法:插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序》 --代码似乎是C语言 ———————— 本文介绍5种常见的排序算法和基于Python实现: 冒泡排序(Bubble Sort&am…...

UML—用例图的那些事
目录 背景: 1.用例图的发展史 过程: 1.用例图中的元素和关系 2.应用中的例子 总结: 背景: 1.用例图的发展史 用例图是一种常用的软件工程工具,用于描述系统的功能需求和用户与系统的交互。它在软件开发过程中起到了重要的作用,并且经历了…...
)
迷宫出口问题求解(DFS)
题面 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 nn 的格点组成,每个格点只有 22 种状态, 00 和 11,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只能移动到东南西北…...

基础算法模板
数据结构 单链表的插入删除 const int N=1e6+10; int head,e[N],ne[N],idx; //head 存储头节点的下标 //idx 存储当前已经用到的那个点 void init() {head=-1;idx=0; } void add_to_head(int x)//插入头节点操作 {e[idx]=x;ne[idx]=head;head=idx;idx++; } void add(int k)/…...

react Ref 的基本使用
类组件中使用ref 在类组件中,你可以使用createRef来创建一个ref,并将它附加到DOM元素或类组件实例上。使用ref允许你在类组件中访问和操作特定的DOM元素或类组件实例。 下面是在类组件中使用ref的步骤: 引入React和createRef: …...
宝塔面板点击SSL闪退打不开怎么解决?
宝塔Linux面板点击SSL证书闪退如何解决?旧版本的宝塔Linux面板确实存在这种情况,如何解决?升级你的宝塔Linux面板即可。新手站长分享宝塔面板SSL闪退的解决方法: 宝塔面板点击SSL证书闪退解决方法 问题:宝塔Linux面板…...

如何将安卓 Gradle 模块打包发布到本地 Maven 仓库
文章目录 具体流程 笔者的运行环境: Android Studio Flamingo | 2022.2.1 Android SDK 33 Gradle 8.0.1 JDK 17 Android 的 Gradle 项目与一般的 Gradle 项目是不同的,因此对将 Gradle 模块打包发布到本地 Maven 仓库来说,对普通 Gradle …...
【Docker】Docker比虚拟机快的原因、ubuntu容器、镜像的分层概念和私有库的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...

java.lang.IllegalArgumentException: Invalid character found in methodname
postman请求异常:java.lang.IllegalArgumentException: Invalid character found in method name. HTTP method names must be tokens...
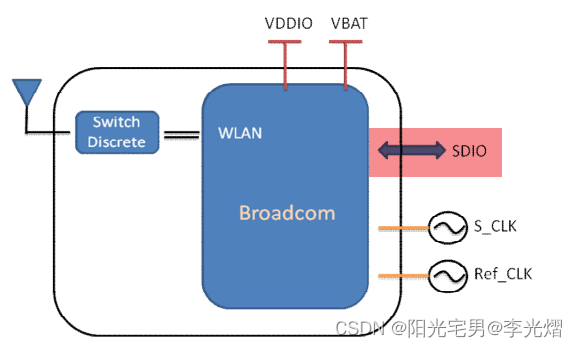
【PCB专题】Allegro高速电路Xnet网络等长约束——SDIO信号为例
高速PCB板布线过程中,经常遇到等长设置问题,例如DDR的一组数据线和地址线等。但是由于数据线和地址线中间有一个电阻(或排阻),这种情况下设置等长就要引入Xnet的概念,通过设置Xnet的等长来确保数据线和地址线的等长。 由无源、分立器件(电阻、电容、电感)连接起来的几段…...
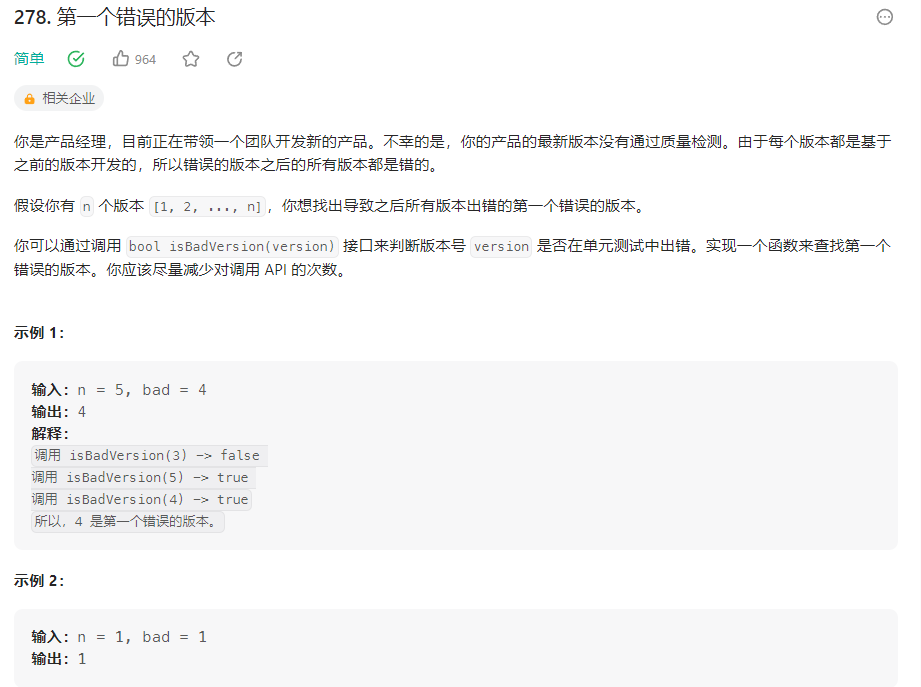
leetcode每日一练-第278题-第一个错误的版本
一、思路 二分查找——因为它可以快速地将版本范围缩小一半,从而更快地找到第一个坏版本。 二、解题方法 维护一个左边界 left 和一个右边界 right,在每一步循环中,我们计算中间版本 mid,然后检查它是否是坏版本。如果是坏版本…...
)
最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树 最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。 换句话说,最小生成树是原图中的一个子图&#…...

4、数据清洗
4、数据清洗 前面我们处理的数据实际上都是已经被处理好的规整数据,但是在大数据整个生产过程中,需要先对数据进行数据清洗,将杂乱无章的数据整理为符合后面处理要求的规整数据。 数据去重 1.删除重复数据groupby().count():可以…...

Python-OpenCV 图像的基础操作
图像的基础操作 获取图像的像素值并修改获取图像的属性信息图像的ROI区域图像通道的拆分及合并图像扩边填充图像上的算术运算图像的加法图像的混合图像的位运算 获取图像的像素值并修改 首先读入一副图像: import numpy as np import cv2# 1.获取并修改像素值 # 读…...

test111
step3:多线程task 首先,实现两个UserService和AsyncUserService两个服务接口: package com.example.demospringboot.service;public interface UserService {void checkUserStatus(); }package com.example.demospringboot.service.impl;im…...
17. Spring 事务
目录 1. 事务定义 2. MySQL 中的事务使用 3. 没有事务时的插入 4. Spring 编程式事务 5. Spring 声明式事务 5.1 Transactional 作用范围 5.2 Transactional 参数说明 5.3 Transactional 工作原理 1. 事务定义 将⼀组操作封装成一个执行单元(封装到一起…...

【C# 基础精讲】运算符和表达式
在C#编程中,运算符和表达式是构建复杂逻辑的关键元素。运算符用于执行各种数学、逻辑和其他操作,而表达式则由运算符、变量、常量和函数组成,用于生成计算结果。本文将详细介绍C#中常见的运算符和表达式的概念,以及它们在程序中的…...

【搜索】DFS连通性模型
算法提高课笔记 目录 迷宫题意思路代码 红与黑题意思路代码 DFS 的搜索分为两大部分: 内部搜索:一个图中从一个点搜到另一个点外部搜索:从一张图(状态)搜到另一张图(状态) 在第一个部分里是图…...

项目优化后续 ,手撸一个精简版VUE项目框架!
之前说过项目之前用的vben框架,在优化完性能后打包效果由原来的纯代码96M变成了56M,后续来啦,通过更换框架,代码压缩到了36M撒花~ 现在就来详细说说是怎么手撸一个框架的! 方案: 搭建一套 vite vue3 a…...
【深度学习笔记】TensorFlow 基础
在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
