迷宫出口问题求解(DFS)
题面
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n×n 的格点组成,每个格点只有 22 种状态, 00 和 11,前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点 A 走到点 B ,问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为 1),则看成无法办到。
输入
第 1 行是一个正整数 n (1≤n≤100),表示迷宫的规模是 n×n 的。
接下来是一个 n×n 的矩阵,矩阵中的元素为 0 或者 1。
再接下来一行是 4 个整数 ha la hb lb,描述 A 处在第ha 行 第 la 列,B 处在第hb 行 第 lb 列。
输出
能办到则输出
YES,否则输出NO。样例
输入
3
0 1 1
0 0 1
1 0 0
1 1 3 3输出
YES
链接:Link.
典中典中典的dfs或bfs题,用dfs做的话要注意边界和到没到达终点。
解法一:到了终点用一个f来标记,true就是到了,false就反之
#include <bits/stdc++.h>
using namespace std;
int a[110][110];
int n , s1 , s2 , e1 , e2;
bool f = false;
int fx[5] = {0 , 0 , 1 , 0 , -1};
int fy[5] = {0 , 1 , 0 , -1 , 0};
void dfs(int x , int y){a[x][y] = 1;int tx , ty;for ( int i = 1 ; i <= 4 ; i++ ){tx = x + fx[i];ty = y + fy[i];if(tx >= 1 && tx <= n && ty >= 1 && ty <= n && a[tx][ty] == 0 ){if(tx == e1 && ty == e2) f = true;else dfs(tx , ty);}}
}
int main(){scanf("%d" , &n);for ( int i = 1 ; i <= n ; i++ )for ( int j = 1 ; j <= n ; j++ )scanf("%d" , &a[i][j]);scanf("%d%d%d%d" , &s1 , &s2 , &e1 , &e2);if ( a[s1][s2] == 1 || a[e1][e2] == 1 )printf("NO");else{dfs(s1 , s2);if ( f == true )printf("YES");elseprintf("NO");}return 0;
}解法二:多加了一个判断条件f==false,这能防止无效递归
#include <bits/stdc++.h>
using namespace std;
int a[110][110];
int n , s1 , s2 , e1 , e2;
bool f = false;
int fx[5] = {0 , 0 , 1 , 0 , -1};
int fy[5] = {0 , 1 , 0 , -1 , 0};
void dfs(int x , int y){a[x][y] = 1;int tx , ty;for ( int i = 1 ; i <= 4 ; i++ ){tx = x + fx[i];ty = y + fy[i];if(tx >= 1 && tx <= n && ty >= 1 && ty <= n && a[tx][ty] == 0 && f == false){if(tx == e1 && ty == e2) f = true;else dfs(tx , ty);}}
}
int main(){scanf("%d" , &n);for ( int i = 1 ; i <= n ; i++ )for ( int j = 1 ; j <= n ; j++ )scanf("%d" , &a[i][j]);scanf("%d%d%d%d" , &s1 , &s2 , &e1 , &e2);if ( a[s1][s2] == 1 || a[e1][e2] == 1 )printf("NO");else{dfs(s1 , s2);if ( f == true )printf("YES\n");elseprintf("NO");}return 0;
} 解法三:到了终点直接输出YES,然后结束整个程序
#include <bits/stdc++.h>
using namespace std;
int a[110][110];
int n , s1 , s2 , e1 , e2;
int fx[5] = {0 , 0 , 1 , 0 , -1};
int fy[5] = {0 , 1 , 0 , -1 , 0};
void dfs(int x , int y){a[x][y] = 1;int tx , ty;for ( int i = 1 ; i <= 4 ; i++ ){tx = x + fx[i];ty = y + fy[i];if(tx >= 1 && tx <= n && ty >= 1 && ty <= n && a[tx][ty] == 0 ){if(tx == e1 && ty == e2) {printf("YES");exit(0); //Í£Ö¹³ÌÐò }else dfs(tx , ty);}}
}
int main(){scanf("%d" , &n);for ( int i = 1 ; i <= n ; i++ )for ( int j = 1 ; j <= n ; j++ )scanf("%d" , &a[i][j]);scanf("%d%d%d%d" , &s1 , &s2 , &e1 , &e2);if ( a[s1][s2] == 1 || a[e1][e2] == 1 )printf("NO");else{dfs(s1 , s2);printf("NO");}return 0;
} 相关文章:
)
迷宫出口问题求解(DFS)
题面 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 nn 的格点组成,每个格点只有 22 种状态, 00 和 11,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只能移动到东南西北…...

基础算法模板
数据结构 单链表的插入删除 const int N=1e6+10; int head,e[N],ne[N],idx; //head 存储头节点的下标 //idx 存储当前已经用到的那个点 void init() {head=-1;idx=0; } void add_to_head(int x)//插入头节点操作 {e[idx]=x;ne[idx]=head;head=idx;idx++; } void add(int k)/…...

react Ref 的基本使用
类组件中使用ref 在类组件中,你可以使用createRef来创建一个ref,并将它附加到DOM元素或类组件实例上。使用ref允许你在类组件中访问和操作特定的DOM元素或类组件实例。 下面是在类组件中使用ref的步骤: 引入React和createRef: …...
宝塔面板点击SSL闪退打不开怎么解决?
宝塔Linux面板点击SSL证书闪退如何解决?旧版本的宝塔Linux面板确实存在这种情况,如何解决?升级你的宝塔Linux面板即可。新手站长分享宝塔面板SSL闪退的解决方法: 宝塔面板点击SSL证书闪退解决方法 问题:宝塔Linux面板…...

如何将安卓 Gradle 模块打包发布到本地 Maven 仓库
文章目录 具体流程 笔者的运行环境: Android Studio Flamingo | 2022.2.1 Android SDK 33 Gradle 8.0.1 JDK 17 Android 的 Gradle 项目与一般的 Gradle 项目是不同的,因此对将 Gradle 模块打包发布到本地 Maven 仓库来说,对普通 Gradle …...
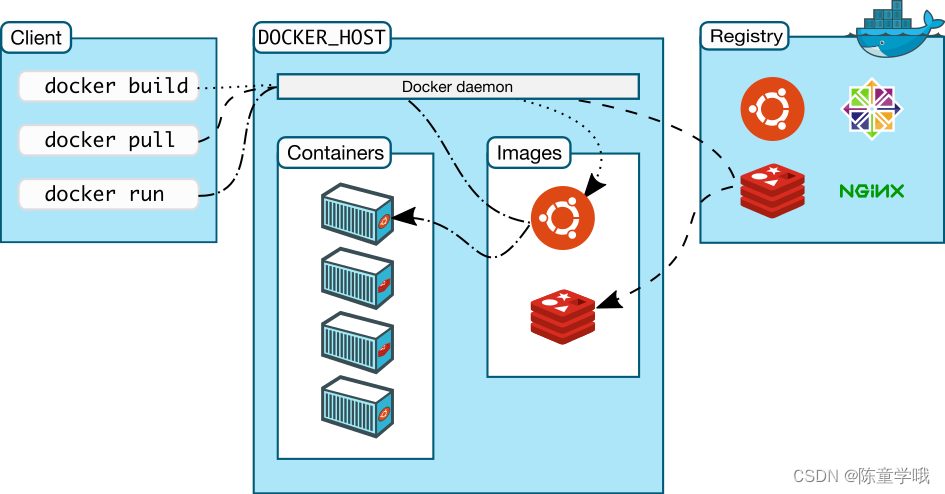
【Docker】Docker比虚拟机快的原因、ubuntu容器、镜像的分层概念和私有库的详细讲解
🚀欢迎来到本文🚀 🍉个人简介:陈童学哦,目前学习C/C、算法、Python、Java等方向,一个正在慢慢前行的普通人。 🏀系列专栏:陈童学的日记 💡其他专栏:CSTL&…...

java.lang.IllegalArgumentException: Invalid character found in methodname
postman请求异常:java.lang.IllegalArgumentException: Invalid character found in method name. HTTP method names must be tokens...
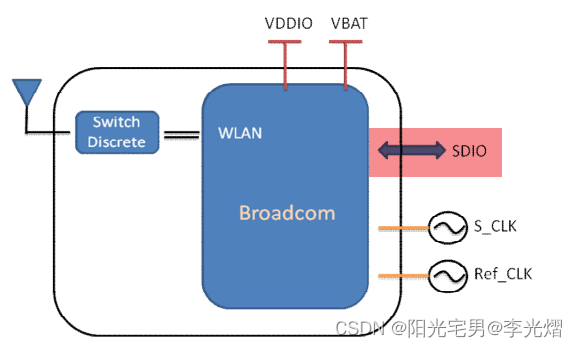
【PCB专题】Allegro高速电路Xnet网络等长约束——SDIO信号为例
高速PCB板布线过程中,经常遇到等长设置问题,例如DDR的一组数据线和地址线等。但是由于数据线和地址线中间有一个电阻(或排阻),这种情况下设置等长就要引入Xnet的概念,通过设置Xnet的等长来确保数据线和地址线的等长。 由无源、分立器件(电阻、电容、电感)连接起来的几段…...
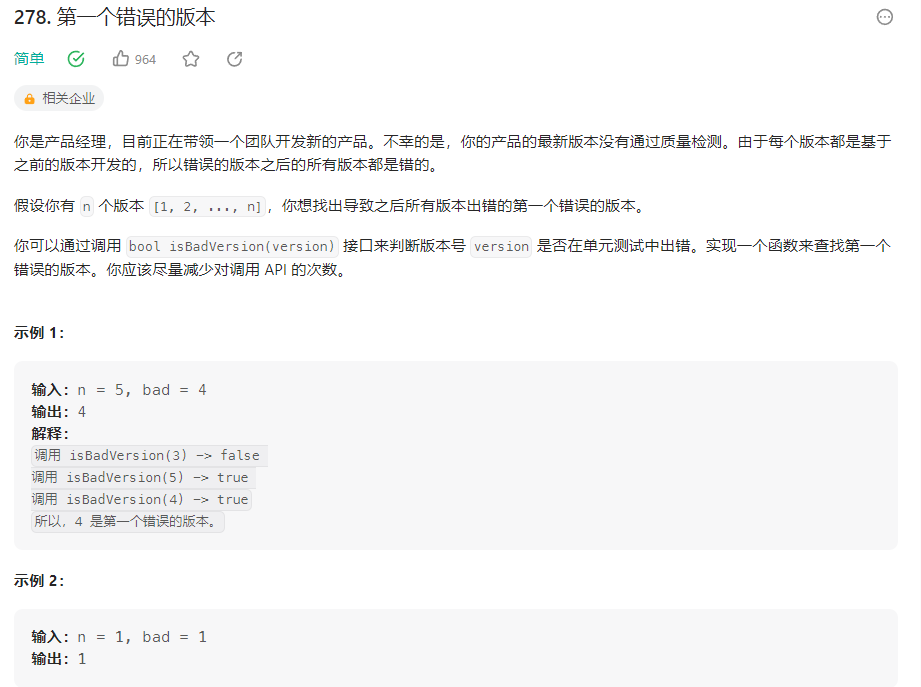
leetcode每日一练-第278题-第一个错误的版本
一、思路 二分查找——因为它可以快速地将版本范围缩小一半,从而更快地找到第一个坏版本。 二、解题方法 维护一个左边界 left 和一个右边界 right,在每一步循环中,我们计算中间版本 mid,然后检查它是否是坏版本。如果是坏版本…...
)
最小生成树笔记(Prim算法Kruskal算法)
1.最小生成树 最小生成树(Minimum Spanning Tree,简称MST)是指:在一个连通无向图中,找到一个包含所有顶点的树,且该树的所有边的权重之和最小。 换句话说,最小生成树是原图中的一个子图&#…...

4、数据清洗
4、数据清洗 前面我们处理的数据实际上都是已经被处理好的规整数据,但是在大数据整个生产过程中,需要先对数据进行数据清洗,将杂乱无章的数据整理为符合后面处理要求的规整数据。 数据去重 1.删除重复数据groupby().count():可以…...

Python-OpenCV 图像的基础操作
图像的基础操作 获取图像的像素值并修改获取图像的属性信息图像的ROI区域图像通道的拆分及合并图像扩边填充图像上的算术运算图像的加法图像的混合图像的位运算 获取图像的像素值并修改 首先读入一副图像: import numpy as np import cv2# 1.获取并修改像素值 # 读…...

test111
step3:多线程task 首先,实现两个UserService和AsyncUserService两个服务接口: package com.example.demospringboot.service;public interface UserService {void checkUserStatus(); }package com.example.demospringboot.service.impl;im…...
17. Spring 事务
目录 1. 事务定义 2. MySQL 中的事务使用 3. 没有事务时的插入 4. Spring 编程式事务 5. Spring 声明式事务 5.1 Transactional 作用范围 5.2 Transactional 参数说明 5.3 Transactional 工作原理 1. 事务定义 将⼀组操作封装成一个执行单元(封装到一起…...

【C# 基础精讲】运算符和表达式
在C#编程中,运算符和表达式是构建复杂逻辑的关键元素。运算符用于执行各种数学、逻辑和其他操作,而表达式则由运算符、变量、常量和函数组成,用于生成计算结果。本文将详细介绍C#中常见的运算符和表达式的概念,以及它们在程序中的…...

【搜索】DFS连通性模型
算法提高课笔记 目录 迷宫题意思路代码 红与黑题意思路代码 DFS 的搜索分为两大部分: 内部搜索:一个图中从一个点搜到另一个点外部搜索:从一张图(状态)搜到另一张图(状态) 在第一个部分里是图…...

项目优化后续 ,手撸一个精简版VUE项目框架!
之前说过项目之前用的vben框架,在优化完性能后打包效果由原来的纯代码96M变成了56M,后续来啦,通过更换框架,代码压缩到了36M撒花~ 现在就来详细说说是怎么手撸一个框架的! 方案: 搭建一套 vite vue3 a…...
【深度学习笔记】TensorFlow 基础
在 TensorFlow 2.0 及之后的版本中,默认采用 Eager Execution 的方式,不再使用 1.0 版本的 Session 创建会话。Eager Execution 使用更自然地方式组织代码,无需构建计算图,可以立即进行数学计算,简化了代码调试的过程。…...

面试题-springcloud中的负载均衡是如何实现的?
一句话导读 Springcloud中的负载均衡是通过Ribbon实现的,自带有很多负载均衡策略,如:包括轮询(Round Robin)、随机(Random)、加权轮询(Weighted Round Robin)、加权随机&…...

flink的ProcessWindowFunction函数的三种状态
背景 在处理窗口函数时,ProcessWindowFunction处理函数可以定义三个状态: 富函数getRuntimeContext.getState, 每个key每个窗口的状态context.windowState(),每个key的状态context.globalState,那么这几个状态之间有什么关系呢? …...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
