矩阵定理复习记录
矩阵复习
矩阵导数定理
若A是一个如下矩阵:
A = [ a 11 a 12 a 21 a 22 ] A= \begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} A=[a11a21a12a22]
y是一个向量矩阵:
y ⃗ = [ y 1 y 2 ] \vec{y}=\begin{bmatrix}y_1\\y_2\end{bmatrix} y=[y1y2]
则可得 text 定理:
δ A ∗ y ⃗ δ y ⃗ = A T \frac{δA*\vec{y}}{δ\vec{y}} = A^T δyδA∗y=AT
δ y ⃗ T ∗ A δ y ⃗ = δ A T ∗ y ⃗ δ y ⃗ = A \frac{δ\vec{y}^T*A}{δ\vec{y}} = \frac{δA^T*\vec{y}}{δ\vec{y}} = A δyδyT∗A=δyδAT∗y=A
也就是对A*y的矩阵,求偏导y,结果为A的转置矩阵;
还可得另一个定理:
δ y ⃗ T ∗ A y ⃗ δ y ⃗ = A y ⃗ + A T y ⃗ \frac{δ\vec{y}^T*A\vec{y}}{δ\vec{y}} = A\vec{y}+ A^T\vec{y} δyδyT∗Ay=Ay+ATy
若A是一个对称矩阵,也就是 A T = A A^T=A AT=A,则上面的还会等于
2 A y ⃗ 2A\vec{y} 2Ay
δ符号表示求导, y ⃗ 表示一个向量 \vec{y}表示一个向量 y表示一个向量
这部分的推导过程可参考此篇视频
矩阵平方定理
若矩阵A满足相乘原则,则有定理:
A 2 = A T ∗ A A^2 = A^T*A A2=AT∗A
单位矩阵
是一种恒等矩阵,对角线上全为1,其余全为0,如下:
I = [ 1 0 0 0 1 0 0 0 1 ] I = \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix} I= 100010001
任何矩阵与单位矩阵相乘等于本身:
A ∗ I = I ∗ A = A A*I = I * A = A A∗I=I∗A=A
逆矩阵
注意逆矩阵不是转置矩阵,若两个矩阵A和B,n*n的方阵,且满足:
A ∗ B = I A*B=I A∗B=I
也就是矩阵相乘等于单位矩阵,也说明A就是B的逆矩阵,A是可逆的,记:B=A^-1
最小二乘法
若输入量为 x 1 , x 2 . . . x n x_1,x_2...x_n x1,x2...xn,输出量为 y 1 , y 2 . . . y n y_1,y_2...y_n y1,y2...yn,为了你和一条函数曲线,是的输入为 x i x_i xi,输出为 y i y_i yi,我们假定它是一个多项式函数如 y i = a x i 2 + b x i + c y_i = ax_i^2 + bx_i + c yi=axi2+bxi+c,x和y都有观察数据,求 a , b , c a,b,c a,b,c,因为数据又多组,带入矩阵中运算:
[ x 1 2 x 1 1 x 2 2 x 2 1 . . . . . . . . . x n 2 x n 2 1 ] [ a b c ] = [ y 1 y 2 . . . y n ] \begin{bmatrix}x_1^2 & x_1&1\\x_2^2&x_2&1\\...&...&...\\x_n^2&x_n^2&1\end{bmatrix}\begin{bmatrix}a\\b\\c\end{bmatrix}= \begin{bmatrix}y_1\\y_2\\...\\y_n\end{bmatrix} x12x22...xn2x1x2...xn211...1 abc = y1y2...yn
进而用X,A,Y替换:
X ∗ A = Y X*A=Y X∗A=Y
A矩阵就是我们要求取的未知参数,往往信号观察是在由噪声的环境中的,假设噪声为V,且噪声的均值为0,也就是正和负噪声,则推导公式:
X ∗ A = Y + V X*A=Y+V X∗A=Y+V
为了使误差最小,使用最小二乘法,二乘差值平方,也就是:
( Y − X ∗ A ) 2 = ( Y − X ∗ A ) T ( Y − X ∗ A ) (Y-X*A)^2 = (Y-X*A)^T(Y-X*A) (Y−X∗A)2=(Y−X∗A)T(Y−X∗A)
对上面的式子A求偏导:
δ ( Y − X ∗ A ) T ( Y − X ∗ A ) δ A \frac{δ(Y-X*A)^T(Y-X*A)}{δA} δAδ(Y−X∗A)T(Y−X∗A)
推导过程可参考此视频最小二乘法讲解,求出后领偏导函数等于0求极值,也就是误差最小值,得到定理:
A = ( X T X ) − 1 X T Y A = (X^TX)^{-1}X^TY A=(XTX)−1XTY
相关文章:

矩阵定理复习记录
矩阵复习 矩阵导数定理 若A是一个如下矩阵: A [ a 11 a 12 a 21 a 22 ] A \begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} A[a11a21a12a22] y是一个向量矩阵: y ⃗ [ y 1 y 2 ] \vec{y}\begin{bmatrix}y_1\\y_2\e…...
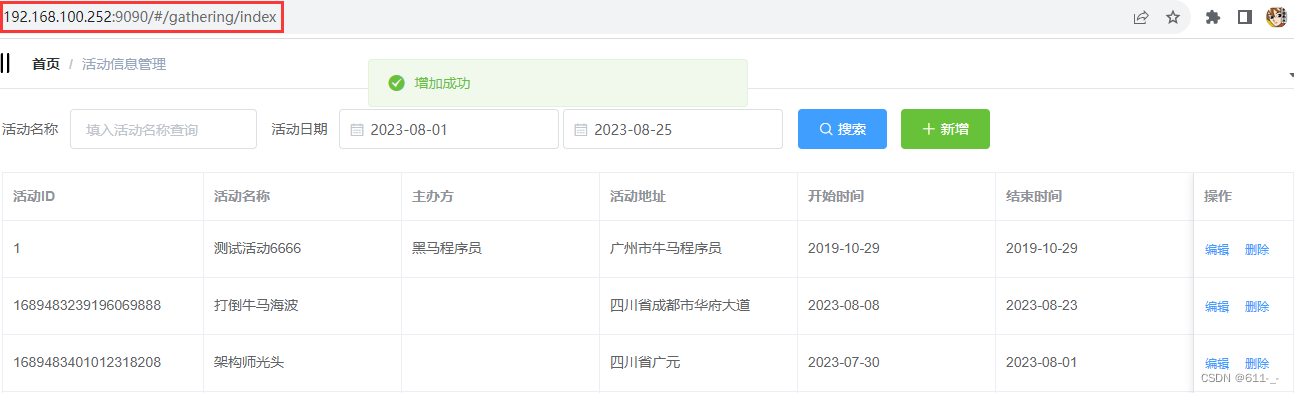
Jenkins+Docker+SpringCloud微服务持续集成项目优化和微服务集群
JenkinsDockerSpringCloud微服务持续集成项目优化和微服务集群 JenkinsDockerSpringCloud部署方案优化JenkinsDockerSpringCloud集群部署流程说明修改所有微服务配置 设计Jenkins集群项目的构建参数编写多选项遍历脚本多项目提交进行代码审查多个项目打包及构建上传镜像把Eurek…...
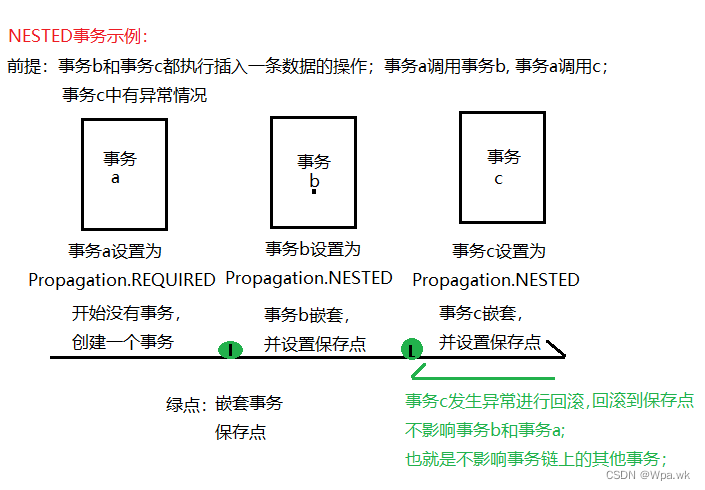
认识 spring 中的事务 与 事务的传播机制
前言 本篇介绍spring中事务的实现方式,如何实现声明式事务,对事物进行参数的设置,了解事务的隔离级别和事务的传播机制;如有错误,请在评论区指正,让我们一起交流,共同进步! 文章目录…...

PHP中的16个危险函数
php中内置了许许多多的函数,在它们的帮助下可以使我们更加快速的进行开发和维护,但是这个函数中依然有许多的函数伴有高风险的,比如说一下的16个函数不到万不得已不尽量不要使用,因为许多“高手”可以通过这些函数抓取你的漏洞。 …...

11、Nvidia显卡驱动、CUDA、cuDNN、Anaconda及Tensorflow Pytorch版本
Nvidia显卡驱动、CUDA、cuDNN、Anaconda及Tensorflow-GPU版本 一、确定版本关系二、安装过程1.安装显卡驱动2、安装CUDA3、安装cudnn4、安装TensorFlow5、安装pytorch 三、卸载 一、确定版本关系 TensorFlow Pytorch推出cuda和cudnn的版本,cuda版本推出驱动可选版本…...

将数据库文件压缩并上传到文件服务器
1.引入上传工具和压缩包工具 <dependency><groupId>org.springframework</groupId><artifactId>spring-test</artifactId> </dependency> <dependency><groupId>com.zlpay</groupId><artifactId>zl-util-fastdfs…...
docker — 容器网络
一、概述 Docker容器每次重启后容器ip是会发生变化的。 这也意味着如果容器间使用ip地址来进行通信的话,一旦有容器重启,重启的容器将不再能被访问到。 而Docker 网络就能够解决这个问题。 Docker 网络主要有以下两个作用: 容器间的互联…...

腾讯面试题:使用Redis分布式锁可能会出现哪些问题?
嗨大家好,我是你们的小米!今天要和大家聊一个有趣的话题,那就是“腾讯面试题:使用Redis做分布式锁可能会出现哪些问题?”没错,就是腾讯大佬们在面试时经常会问到的一个问题,我们来一起深入了解一…...
直接在html中引入Vue.js的cdn来实现Vue3的组合式API
Vue3的组合式API是使用setup函数来编写组件逻辑的。setup函数是Vue3中用于替代Vue2的选项API(如data、methods等)的一种方式。在setup函数中,你可以访问到一些特殊的响应式对象,并且可以返回一些可以在模板中使用的数据、方法等。…...
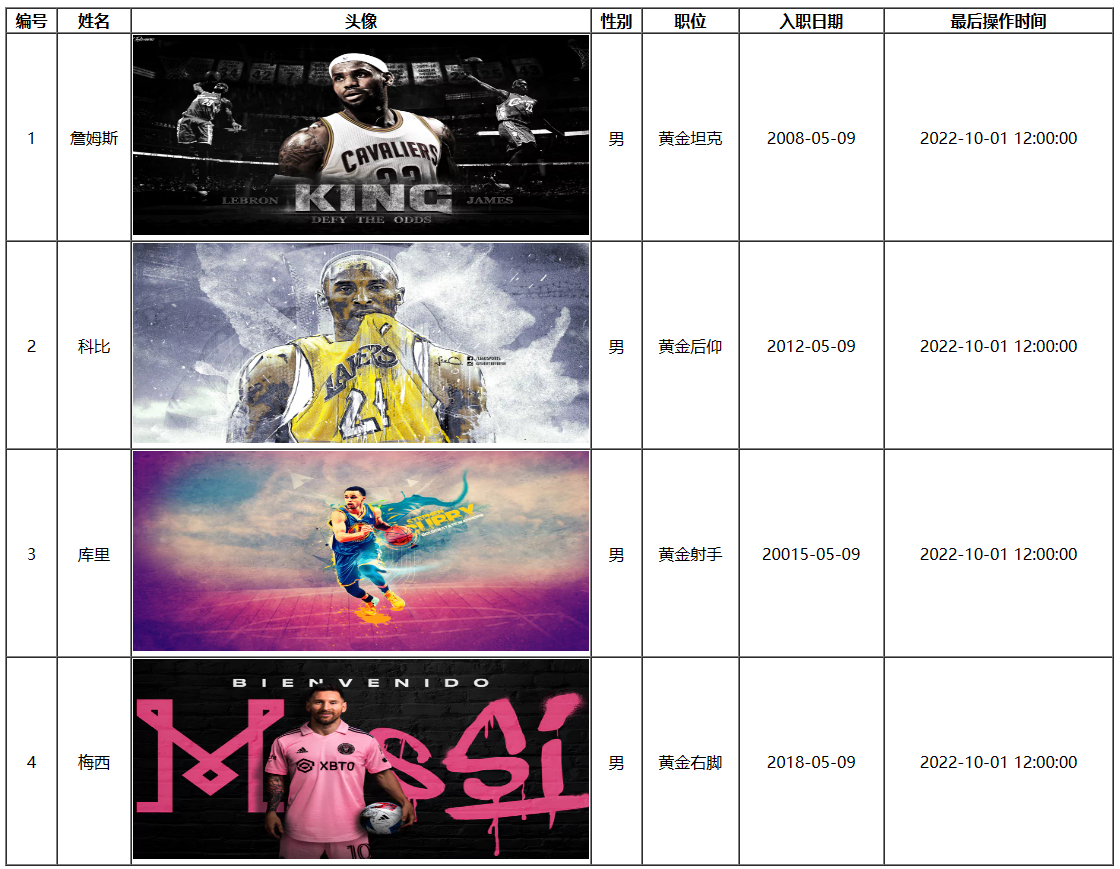
YAPi在线接口文档简单案例(结合Vue前端Demo)
在前后端分离开发中,我们都是基于文档进行开发,那前端人员有时候无法马上拿到后端的数据,该怎么办?我们一般采用mock模拟伪造数据直接进行测试,本篇文章主要介绍YApi在线接口文档的简单使用,并结合Vue的小d…...

Java基础篇--Runtime类
介绍 Runtime类用于表示虚拟机运行时的状态,它用于封装JVM虚拟机进程。每次使用java命令启动虚拟机都对应一个Runtime实例,并且只有一个实例。 因此在Runtime类定义的时候,它的构造方法已经被私有化了(单例设计模式的应用),对象…...

数字后端笔试题(1)DCG后congestion问题
我正在「拾陆楼」和朋友们讨论有趣的话题,你⼀起来吧? 拾陆楼知识星球入口 已知某模块的DCG结果显示存在congestion,有congestion部分逻辑结构如下图: 问题1: 如何分析该电路有congestion问题的原因? 答:data selecti…...

数据结构:交换排序
冒泡排序 起泡排序,别名“冒泡排序”,该算法的核心思想是将无序表中的所有记录,通过两两比较关键字,得出升序序列或者降序序列。 算法步骤 比较相邻的元素。如果第一个元素大于第二个元素,就交换它们。对每一对相邻…...
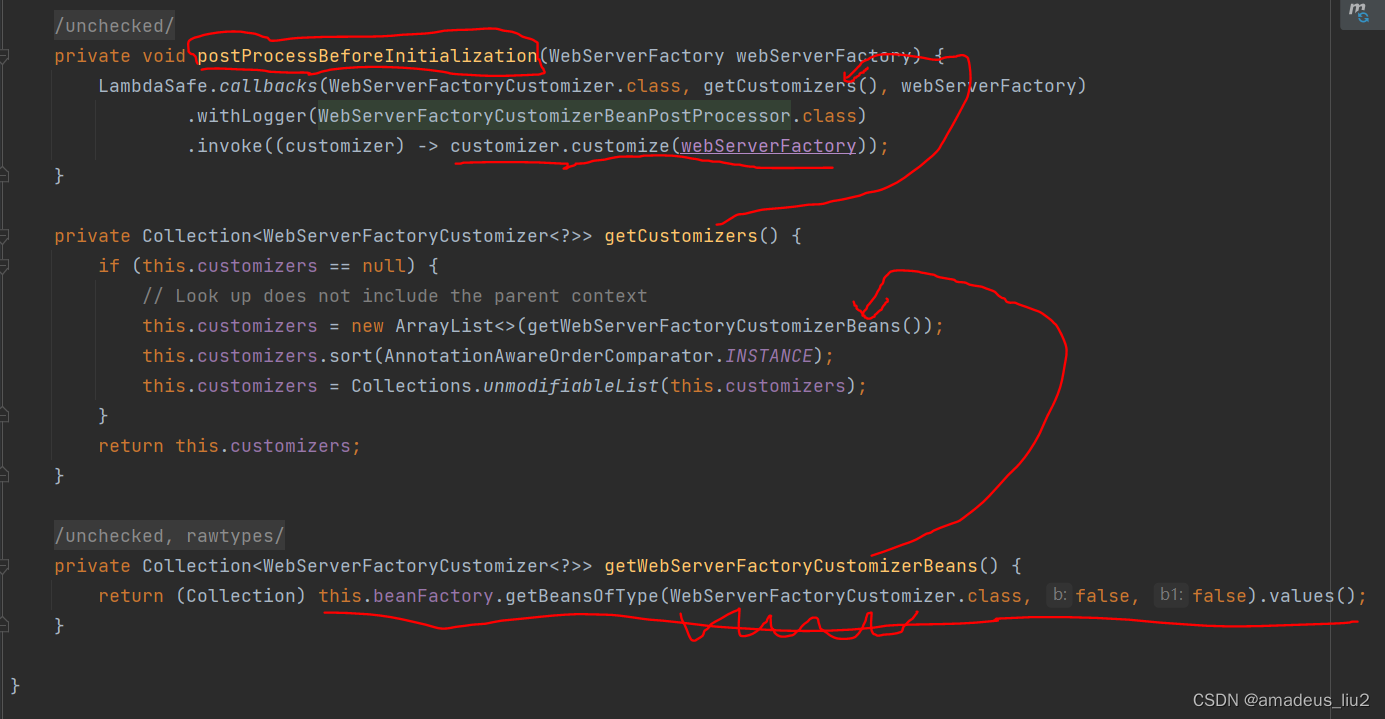
SpringBoot复习:(42)WebServerCustomizer的customize方法是在哪里被调用的?
ServletWebServletAutoConfiguration类定义如下: 可以看到其中通过Import注解导入了其内部类BeanPostProcessorRegister。 BeanPostProcessor中定义的registerBeanDefinition方法会被Spring容器调用。 registerBeanDefinitions方法调用了RegistrySyntheticBeanIf…...

年至年的选择仿elementui的样式
组件:<!--* Author: liuyu liuyuxizhengtech.com* Date: 2023-02-01 16:57:27* LastEditors: wangping wangpingxizhengtech.com* LastEditTime: 2023-06-30 17:25:14* Description: 时间选择年 - 年 --> <template><div class"yearPicker"…...
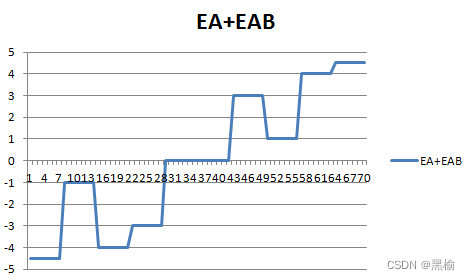
分类过程中的一种遮挡现象
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 让网络的输入只有3个节点,AB训练集各由6张二值化的图片组成,让A,B中各有3个点,且不重合,统计迭代次数并排序。 其中有10组数据 差值结构 迭代次数 构造平均列A 构造平均列AB…...

下一代服务架构:单体架构-->分布式架构-->微服务(DDD)-->软件定义架构(SDF with GraphEngine)
参考:自己实现一个SQL解析引擎_曾经的学渣的博客-CSDN博客...
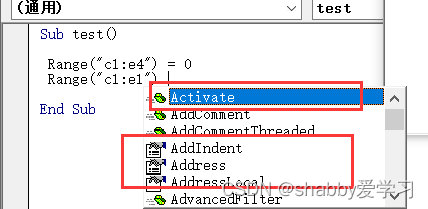
excel 之 VBA
1、excel和VBA 高效办公,把重复性的工作写成VBA代码(VB代码的衍生物,语法和VBA相同)。 首先打开开发工具模式,如果没有选显卡,需要手动打开 打开程序编辑界面 快捷键 altF11一般操作 程序调试…...
【数学建模】--聚类模型
聚类模型的定义: “物以类聚,人以群分”,所谓的聚类,就是将样本划分为由类似的对象组成的多个类的过程。聚类后,我们可以更加准确的在每个类中单独使用统计模型进行估计,分析或预测;也可以探究不…...

css3新增选择器总结
目录 一、属性选择器 二、结构伪类选择器 三、伪元素选择器 四、UI状态伪类选择器 五、反选伪类选择器 六、target选择器 七、父亲选择器、后代选择器 八、相邻兄弟选择器、兄弟们选择器 一、属性选择器 (除IE6外的大部分浏览器支持) E&#…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...
