深度学习Batch Normalization
批标准化(Batch Normalization,简称BN)是一种用于深度神经网络的技术,它的主要目的是解决深度学习模型训练过程中的内部协变量偏移问题。简单来说,当我们在训练深度神经网络时,每一层的输入分布都可能会随着前一层参数的更新而发生变化,这种变化会导致训练过程变得不稳定。BN通过对每一层的输入进行标准化,使其均值为0,方差为1,从而使得网络在每一层都能接收到相对稳定的数据分布。
BatchNorm1d
对2d或3d数据进行批标准化(Batch Normlization)操作:
class torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True):
参数:
1.num_features:特征的维度 ( N , L ) − > L ; ( N , C , L ) − > C (N,L) -> L ;(N,C,L) -> C (N,L)−>L;(N,C,L)−>C
2.eps:在分母上添加一个定值,不能趋近于0
3.momentum:动态均值和动态方差所使用的动量,这里的momentum是对均值和方差进行的滑动平均。即 μ 1 = ( 1 − m o m e n t u m ) ∗ μ l a s t + m o m e n t u m ∗ μ μ_1 = (1 - momentum)* μ_{last} + momentum * μ μ1=(1−momentum)∗μlast+momentum∗μ,这里μ1为输出值,μ_last为上一次的计算值,μ为真实计算的值
4.affine:布尔变量,是否为该层添加可学习的仿设变换,仿射变换的系数即为下式的gamma和beta
原理:
计算各个维度的均值和标准差: y = x − mean [ x ] Var [ x ] + ϵ ∗ g a m m a + beta y=\frac{x-\operatorname{mean}[x]}{\sqrt{\operatorname{Var}[x]}+\epsilon} * g a m m a+\text { beta } y=Var[x]+ϵx−mean[x]∗gamma+ beta
m = nn.BatchNorm1d(5, affine=False)
m1 = nn.BatchNorm1d(5, affine=True)
input = autograd.Variable(torch.randn(5, 5))
output = m(input)
output1 = m1(input)
print(input, '\n',output,'\n',output1)tensor([[-0.6046, -0.8939, 1.3246, 0.2621, 1.0777],[ 0.9088, -0.6219, 0.9589, 0.7307, 0.5221],[ 1.7435, 0.6662, -0.5827, 0.3325, -0.8179],[-0.2250, 0.9930, 0.0504, -0.4509, 1.6605],[-0.5742, 1.6543, 0.6083, 0.5746, -0.3208]]) tensor([[-0.9212, -1.2920, 1.2648, -0.0680, 0.7249],[ 0.7107, -1.0117, 0.7224, 1.0842, 0.1085],[ 1.6108, 0.3161, -1.5642, 0.1049, -1.3780],[-0.5119, 0.6530, -0.6252, -1.8215, 1.3713],[-0.8885, 1.3345, 0.2022, 0.7005, -0.8266]]) tensor([[-0.9212, -1.2920, 1.2648, -0.0680, 0.7249],[ 0.7107, -1.0117, 0.7224, 1.0842, 0.1085],[ 1.6108, 0.3161, -1.5642, 0.1049, -1.3780],[-0.5119, 0.6530, -0.6252, -1.8215, 1.3713],[-0.8885, 1.3345, 0.2022, 0.7005, -0.8266]],grad_fn=<NativeBatchNormBackward>)BatchNorm2d
对小批量(mini-batch)3d数据组成的4d输入进行批标准化(Batch Normalization)操作
class torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True):
1.num_features: 来自期望输入的特征数,C from an expected input of size (N,C,H,W)
2.eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5.
3.momentum: 动态均值和动态方差所使用的动量。默认为0.1.
4.affine: 一个布尔值,当设为true,给该层添加可学习的仿射变换参数。
原理:
计算各个维度的均值和标准差: y = x − mean [ x ] Var [ x ] + ϵ ∗ g a m m a + beta y=\frac{x-\operatorname{mean}[x]}{\sqrt{\operatorname{Var}[x]}+\epsilon} * g a m m a+\text { beta } y=Var[x]+ϵx−mean[x]∗gamma+ beta
m = nn.BatchNorm2d(2, affine=False)
m1 = nn.BatchNorm2d(2, affine=True)
input = autograd.Variable(torch.randn(1,2,5, 5))
output = m(input)
output1 = m1(input)
print(input, '\n',output,'\n',output1)tensor([[[[-0.2606, -0.8874, 0.8364, 0.0184, 0.8040],[ 1.0593, -0.6811, 1.3497, -0.6840, -2.0859],[-0.5399, 1.3321, -0.6281, -0.9044, 1.7491],[ 0.7559, 0.5607, -0.0447, -0.3868, 1.2404],[ 1.2078, -0.9642, 0.3980, 0.2087, -1.3940]],[[ 0.0493, 0.7372, 1.1964, 0.3862, 0.9900],[ 0.3544, 0.1767, -1.5780, 0.1642, -2.1586],[-0.4891, -0.7272, 1.6860, -1.6091, 0.9730],[-2.4161, -2.2096, 0.4617, -0.2965, -0.5663],[-0.0222, -0.7628, 0.6404, -1.4428, 0.5750]]]]) tensor([[[[-0.3522, -0.9959, 0.7743, -0.0657, 0.7410],[ 1.0032, -0.7840, 1.3015, -0.7870, -2.2266],[-0.6390, 1.2833, -0.7296, -1.0134, 1.7116],[ 0.6917, 0.4912, -0.1305, -0.4818, 1.1892],[ 1.1557, -1.0748, 0.3242, 0.1298, -1.5161]],[[ 0.2560, 0.8743, 1.2870, 0.5588, 1.1015],[ 0.5302, 0.3705, -1.2066, 0.3593, -1.7285],[-0.2280, -0.4420, 1.7271, -1.2346, 1.0862],[-1.9599, -1.7743, 0.6266, -0.0549, -0.2974],[ 0.1917, -0.4739, 0.7873, -1.0852, 0.7285]]]]) tensor([[[[-0.3522, -0.9959, 0.7743, -0.0657, 0.7410],[ 1.0032, -0.7840, 1.3015, -0.7870, -2.2266],[-0.6390, 1.2833, -0.7296, -1.0134, 1.7116],[ 0.6917, 0.4912, -0.1305, -0.4818, 1.1892],[ 1.1557, -1.0748, 0.3242, 0.1298, -1.5161]],[[ 0.2560, 0.8743, 1.2870, 0.5588, 1.1015],[ 0.5302, 0.3705, -1.2066, 0.3593, -1.7285],[-0.2280, -0.4420, 1.7271, -1.2346, 1.0862],[-1.9599, -1.7743, 0.6266, -0.0549, -0.2974],[ 0.1917, -0.4739, 0.7873, -1.0852, 0.7285]]]],grad_fn=<NativeBatchNormBackward>)
使用
用的地方通常在一个全连接或者卷积层与激活函数中间,即 (全连接/卷积)—- BatchNorm —- 激活函数。但也有人说把 BatchNorm 放在激活函数后面效果更好,可以都试一下。
BN的作用:
- 加速训练:BN可以使得网络的训练速度更快。因为经过标准化后,权重的更新方向更加明确,可以使用更大的学习率进行训练。
- 正则化效果:BN具有轻微的正则化效果,可以在一定程度上防止模型过拟合。
- 允许使用各种激活函数:在没有BN之前,某些激活函数(如sigmoid和tanh)在深层网络中容易导致梯度消失或梯度爆炸。但使用BN后,这些问题得到了缓解,因为数据分布被标准化了。
为什么要用
BN的作用:
- 加速训练:BN可以使得网络的训练速度更快。因为经过标准化后,权重的更新方向更加明确,可以使用更大的学习率进行训练。
- 正则化效果:BN具有轻微的正则化效果,可以在一定程度上防止模型过拟合。
- 允许使用各种激活函数:在没有BN之前,某些激活函数(如sigmoid和tanh)在深层网络中容易导致梯度消失或梯度爆炸。但使用BN后,这些问题得到了缓解,因为数据分布被标准化了。
参考
(31条消息) BatchNorm2d原理、作用及其pytorch中BatchNorm2d函数的参数讲解_LS_learner的博客-CSDN博客_batchnorm2d
(31条消息) pytorch中批量归一化BatchNorm1d和BatchNorm2d函数_小白827的博客-CSDN博客_batchnorm1d 2d
BatchNorm 到底应该怎么用? - 项脊轩的琵琶树 (gitee.io)
相关文章:

深度学习Batch Normalization
批标准化(Batch Normalization,简称BN)是一种用于深度神经网络的技术,它的主要目的是解决深度学习模型训练过程中的内部协变量偏移问题。简单来说,当我们在训练深度神经网络时,每一层的输入分布都可能会随着…...

el-table实现懒加载(el-table-infinite-scroll)
2023.8.15今天我学习了用el-table对大量的数据进行懒加载。 效果如下: 1.首先安装: npm install --save el-table-infinite-scroll2 2.全局引入: import ElTableInfiniteScroll from "el-table-infinite-scroll";// 懒加载 V…...

vueRouter回顾
关于vueRouter的两种路由模式 “history” 模式使用正常的 URL 格式,例如 https://example.com/path。“hash” 模式将路由信息添加到 URL 的哈希部分(#)后面,例如 https://example.com/#/path。 1、history模式:没有…...

大规模无人机集群算法flocking(蜂群)
matlab2016b正常运行...
【第三阶段】kotlin语言的split
const val INFO"kotlin,java,c,c#" fun main() {//list自动类型推断成listList<String>val listINFO.split(",")//直接输出list集合,不解构println("直接输出list的集合元素:$list")//类比c有解构,ktoli…...
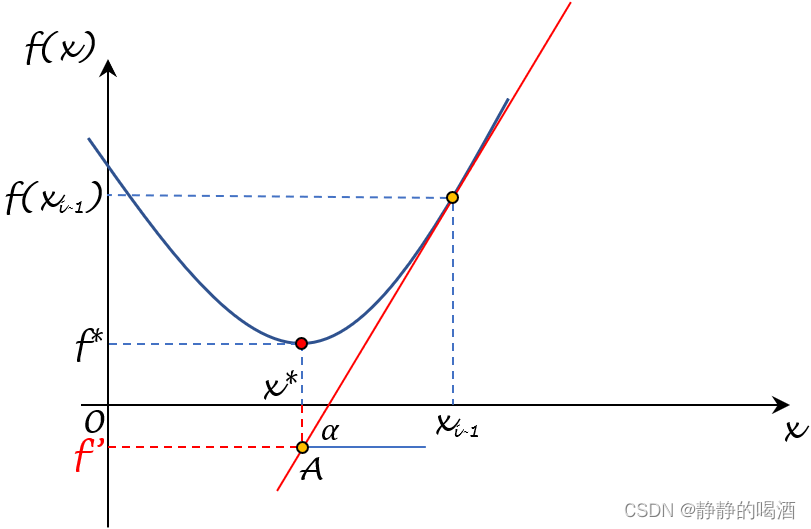
机器学习笔记值优化算法(十四)梯度下降法在凸函数上的收敛性
机器学习笔记之优化算法——梯度下降法在凸函数上的收敛性 引言回顾:收敛速度:次线性收敛二次上界引理 梯度下降法在凸函数上的收敛性收敛性定理介绍证明过程 引言 本节将介绍梯度下降法在凸函数上的收敛性。 回顾: 收敛速度:次…...
iphone拷贝照片中间带E自动去重软件,以及java程序如何打包成jar和exe
文章目录 一、前提二、问题描述三、原始处理方式四、程序处理4.1 java程序如何打包exe4.1.1 首先打包jar4.1.2 开始生成exe4.1.3 软件使用方式 4.2 更换图标4.2.1 更换swing的打包jar图标4.2.2 更换exe图标 4.3 如何使生成的exe在没有java环境的电脑上运行4.3.1 Inno Setup打包…...

不同分类器对数据的处理
"""基于鸢尾花的不同分类器的效果比对:step1:准备数据;提取数据的特征向量X,Y将Y数据采用LabelEncoder转化为数值型数据;step2:将提取的特征向量X,Y进行拆分(训练集与测试集)step3:构建不同分类器并设置参数,例如:…...

十面骰子、
十面骰子(一): v 有一个十面的骰子,每一面分别为1-10,不断投掷骰子,投10000次,统计每一面1-10出现的次数或概率. v 提示:可用rand()产生1-10之间的随机数,再统计1-10出现的机会,存放于数组里,…...
IDE的下载和使用
IDE 文章目录 IDEJETBRAIN JETBRAIN 官网下载对应的ide 激活方式 dxm的电脑已经把这个脚本下载下来了,脚本是macjihuo 以后就不用买了...

华为OD机试真题【字母组合】
1、题目描述 【字母组合】 数字0、1、2、3、4、5、6、7、8、9分别关联 a~z 26个英文字母。 0 关联 “a”,”b”,”c” 1 关联 “d”,”e”,”f” 2 关联 “g”,”h”,”i” 3 关联 “j”,”k”,”l” 4 关联 “m”,”n”,”o” 5 关联 “p”,”q”,”r” 6 关联 “s”,”t” 7…...
Midjourney Prompt 提示词速查表 v5.2
Midjourney 最新的版本更新正不断推出令人兴奋的新功能。这虽然不断扩展了我们的AI绘图工具箱,但有时也会让我们难以掌握所有实际可以使用的功能和参数。 针对此问题, 小编整理了 "Midjourney Prompt 提示词速查表",这是一个非常方便的 Midjo…...

自动驾驶——驶向未来的革命性技术
自动驾驶——驶向未来的革命性技术 自动驾驶的组件自动驾驶的优势自动驾驶的应用自动驾驶的未来中国的自动驾驶 自动驾驶是一种技术,它允许车辆在没有人类驾驶员的情况下自主地进行行驶。它利用各种传感器、计算机视觉、人工智能和机器学习算法来感知和理解周围环境…...
 甲级 1004 Counting Leaves)
PAT (Advanced Level) 甲级 1004 Counting Leaves
点此查看所有题目集 A family hierarchy is usually presented by a pedigree tree. Your job is to count those family members who have no child. Input Specification: Each input file contains one test case. Each case starts with a line containing 0<N<100, …...
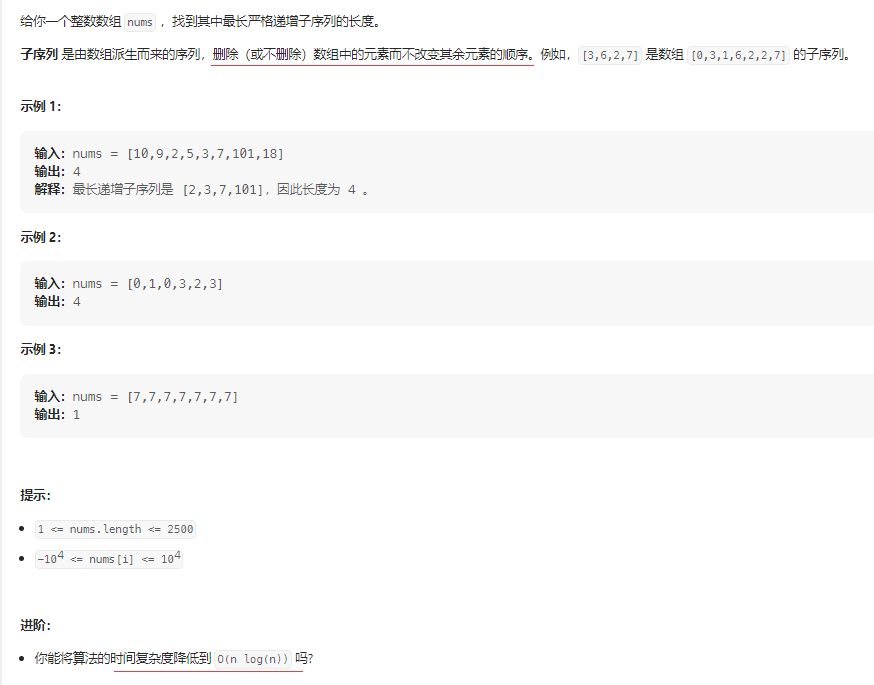
最长递增子序列——力扣300
int lengthOfLIS(vector<int>& nums) {int len=1, n=nums.size();if...

邮递员送信 单源最短路+反向建边
有一个邮递员要送东西,邮局在节点 1 1 1。他总共要送 n − 1 n−1 n−1样东西,其目的地分别是节点 2 2 2到节点 n n n。所有的道路都是单行的,共有 m m m条道路。邮递员每次只能带一样东西,运送每件物品过后必须返回邮局。求送完东…...

git的常用操作
1. git查看dev分支与master分支的情况 要查看特定分支(如dev和master)的情况,您可以使用以下命令: git log --oneline master..dev 这将显示在dev分支上存在但不在master分支上的提交记录的简要信息。每条记录都包括提交的哈希…...
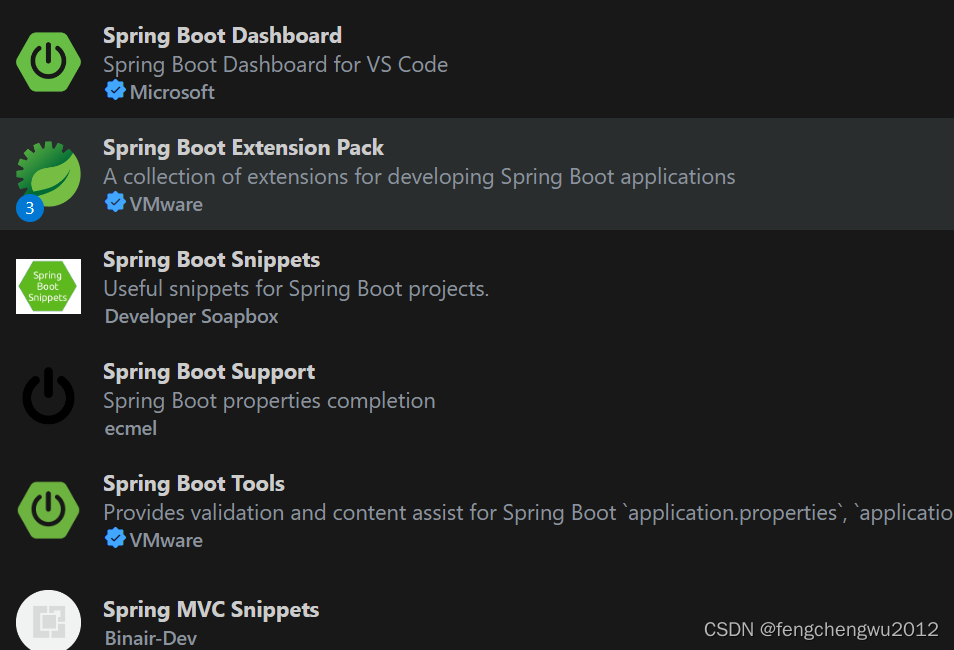
vscode搭建java开发环境
一、配置extensions环境变量VSCODE_EXTENSIONS, 该环境变量路径下的存放安装组件: 二、setting配置文件 {"java.jdt.ls.java.home": "e:\\software\\jdk\\jdk17",// java运行环境"java.configuration.runtimes": [{"…...

01 qt快速入门
一 qt介绍 1.基本概念 1991年由Qt Company(奇趣)开发的跨平台C++图形用户界面应用程序开发框架,GUI程序和非GUI程序。优点:一套源码在不同的平台通过不同的编译器进行编译,就可以运行到该平台上目标机。面向对象的封装机制来对其接口封装。 GUI —图形用户界面(Graphic…...

嵌入式开发中常用且杂散的命令
1、mount命令 # 挂载linux系统 mkdir /tmp/share mount -t nfs 10.77.66.88:/share/ /tmp/share -o nolock,tcp cd /tmp/share# 挂载Windows系统 mkdir /tmp/windows mount -t nfs 10.66.77.88:/c/public /tmp/windows -o nolock,tcp cd /tmp/windows# 挂载vfat格式的U盘 mkdi…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...
