一元三次方程的解
一元三次方程的解法,点击跳转知乎原文地址
(一)一元三次方程降阶
一元三次方程原型:
a x 3 + b x 2 + c x + d = 0 a x^3 + b x^2 + cx + d = 0 ax3+bx2+cx+d=0
代换削元。最简单的方法是线性变化削元。假设x = my + n, 带入后可以削去未知数y的平方项:
a ( m y + n ) 3 + b ( m y + n ) 2 + c ( m y + n ) + d = a m 3 y 3 + 3 a m 2 y 2 n + 3 a m y n 2 + a n 3 + b m 2 y 2 + 2 b m n y + b n 2 + c m y + c n + d = 0 a (my+n) ^3 + b (my+n) ^ 2 + c(my+n) + d = \\ am^3y^3 + 3am^2y^2 n + 3amyn^2 + an^3 +\\ bm^2y^2 + 2bmny+bn^2 +\\ cmy+cn +\\ d = 0 a(my+n)3+b(my+n)2+c(my+n)+d=am3y3+3am2y2n+3amyn2+an3+bm2y2+2bmny+bn2+cmy+cn+d=0
即此时必须满足二次项系数值之和为0,也就是 3 a m 2 n + b m 2 = 0 3am^2n + bm^2 = 0 3am2n+bm2=0,从而可以得出结论: n = − b 3 a , m 为任意值 n = - \frac {b}{3a},m为任意值 n=−3ab,m为任意值
由此证明:若将 x = y − b 3 a x = y - \frac {b}{3a} x=y−3ab带入原式,则可以讲方程变为如下形式:
x 3 + p x + q = 0 (1.0) x ^ 3 + p x + q = 0 \tag{1.0} x3+px+q=0(1.0)
(二)一元三次方程解的原理
上一片博文是我学习接触一元三次方程的起点,但是原文中有几句话一直不是很明白,为什么x = a + b带入后的限制条件为什么是:
- − 3 a b = p -3ab = p −3ab=p
- q = − ( a 3 + b 3 ) q = - (a^3 + b^3) q=−(a3+b3)
- x = a + b x = a+ b x=a+b
看了另外一篇文章,加上自己的思索终于弄明白了。手动推导一下。
其中要解的方程如下:
x 3 + p x + q = 0 (1.0) x ^ 3 + p x + q = 0 \tag{1.0} x3+px+q=0(1.0)
假设 x = a + b x = a+b x=a+b ,那么
x 3 = ( a + b ) 3 = a 3 + 3 a b ( a + b ) + b 3 = a 3 + b 3 + 3 a b x x^3 = (a+b)^3 = a^3 + 3ab(a+b) + b^3 = a^3 + b^3 + 3ab x x3=(a+b)3=a3+3ab(a+b)+b3=a3+b3+3abx
因此 x 3 − 3 a b x − ( a 3 + b 3 ) = 0 (1.1) x ^ 3 - 3abx - (a^3 + b^3 ) = 0 \tag{1.1} x3−3abx−(a3+b3)=0(1.1)
仔细观察上面的(1.0)和 (1.1),因为两个式子差别仅仅是一个代换问题,如果代换成立的话(必然可以成立),两者是等价的;也可以认为,未知数的次数和系数形式是一样的,由此得到如下结论:
- − 3 a b = p -3ab = p −3ab=p
- q = − ( a 3 + b 3 ) q = - (a^3 + b^3) q=−(a3+b3)
- x = a + b x = a+ b x=a+b
如此一来,我们假设 x = a + b, 带入要解的方程中可得:
( a + b ) 3 + p ( a + b ) + q = 0 = = > (a + b) ^ 3 + p(a+b) + q = 0 ==> (a+b)3+p(a+b)+q=0==>
a 3 + b 3 + 3 a 2 b + 3 a b 2 + p ( a + b ) + a = 0 = = > a^3 + b^3 + 3 a^2b + 3ab^2 + p(a+b) + a = 0 ==> a3+b3+3a2b+3ab2+p(a+b)+a=0==>
a 3 + b 3 + ( a + b ) ( 3 a b + p ) + q = 0 (1.2) a^3 + b^3 + (a+b)(3ab + p) + q = 0 \tag{1.2} a3+b3+(a+b)(3ab+p)+q=0(1.2)
此时,上述三个条件依然是满足的。未知数变为a 和 b,其满足的关系为:
- a 3 b 3 = − p 3 27 a^3b^3 = - \frac{p^3}{27} a3b3=−27p3
- a 3 + b 3 = − q a^3 + b^3 = -q a3+b3=−q
到现在为止,就可以讲三次方程转化为2次方程来求解了。
再次假设: a 3 = m , b 3 = n a^3 = m, b^3 = n a3=m,b3=n,带入后可得: m ( − q − m ) = − p 3 27 m(-q - m) = -\frac{p^3}{27} m(−q−m)=−27p3
即 m 2 + m q − p 3 / 27 = 0 m^2 + mq - p^3/27 = 0 m2+mq−p3/27=0
m = − q + − q 2 + 4 p 3 27 2 = − q / 2 + − ( q 2 ) 2 + ( p 3 ) 3 m = \frac{-q+-\sqrt{q^2+\frac{4p^3}{27}}}{2} = -q/2 +- \sqrt{ (\frac{q}{2})^2 + (\frac{p}{3})^3} m=2−q+−q2+274p3=−q/2+−(2q)2+(3p)3
n = − q / 2 − + ( q 2 ) 2 + ( p 3 ) 3 n = -q/2 -+ \sqrt{ (\frac{q}{2})^2 + (\frac{p}{3})^3} n=−q/2−+(2q)2+(3p)3
将上面两个变量开三次方可得方程的一个根:
a = − q / 2 + − ( q 2 ) 2 + ( p 3 ) 3 3 a= \sqrt[3]{ -q/2 +- \sqrt{ (\frac{q}{2})^2 + (\frac{p}{3})^3}} a=3−q/2+−(2q)2+(3p)3
b = − q / 2 − + ( q 2 ) 2 + ( p 3 ) 3 3 b = \sqrt[3] { -q/2 -+ \sqrt{ (\frac{q}{2})^2 + (\frac{p}{3})^3} } b=3−q/2−+(2q)2+(3p)3
(三)其他的根
在获取了方程的一个根后,利用等式 a 3 + b 3 = − q a^3 + b^3 = -q a3+b3=−q和 a b = − p 3 ab = - \frac {p}{3} ab=−3p可以得到其他的两个根。
a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) = − q a^3 + b^3 = (a + b)(a ^2 - ab + b^2) = -q a3+b3=(a+b)(a2−ab+b2)=−q
a 2 − a b + b 2 = − q a + b a ^2 - ab + b^2= \frac {-q}{a + b} a2−ab+b2=a+b−q
a b = − p 3 ab = - \frac {p}{3} ab=−3p
相关文章:

一元三次方程的解
一元三次方程的解法,点击跳转知乎原文地址 (一)一元三次方程降阶 一元三次方程原型: a x 3 b x 2 c x d 0 a x^3 b x^2 cx d 0 ax3bx2cxd0 代换削元。最简单的方法是线性变化削元。假设x my n, 带入后可以削去未知数…...
aardio开发语言Excel数据表读取修改保存实例练习
import win.ui; /*DSG{{*/ var winform win.form(text"aardio form";right759;bottom479) winform.add( buttonEnd{cls"button";text"末页";left572;top442;right643;bottom473;z6}; buttonExcelRead{cls"button";text"读取Exce…...
webshell绕过
文章目录 webshell前置知识进阶绕过 webshell 前置知识 <?phpecho "A"^""; ?>运行结果 可以看到出来的结果是字符“!”。 为什么会得到这个结果?是因为代码的“A”字符与“”字符产生了异或。 php中,两个变…...
Spring Boot 统一功能处理
目录 1.用户登录权限效验 1.1 Spring AOP 用户统一登录验证的问题 1.2 Spring 拦截器 1.2.1 自定义拦截器 1.2.2 将自定义拦截器加入到系统配置 1.3 拦截器实现原理 1.3.1 实现原理源码分析 2. 统一异常处理 2.1 创建一个异常处理类 2.2 创建异常检测的类和处理业务方法 3. 统一…...
图像处理常见的两种拉流方式
传统算法或者深度学习在进行图像处理之前,总是会首先进行图像的采集,也就是所谓的拉流。解决拉流的方式有两种,一个是直接使用opencv进行取流,另一个是使用ffmpeg进行取流,如下分别介绍这两种方式进行拉流处理。 1、o…...

数据可视化数据调用浅析
数据可视化是现代数据分析和决策支持中不可或缺的一环。它将数据转化为图形、图表和可视化工具,以便更直观地理解和解释数据。在数据可视化的过程中,数据的调用和准备是关键的一步。本文将探讨数据可视化中的数据调用过程,并介绍一些常用的数…...
恒运资本:CPO概念发力走高,兆龙互联涨超10%,华是科技再创新高
CPO概念15日盘中发力走高,截至发稿,华是科技涨超15%再创新高,兆龙互联涨逾11%,中贝通讯涨停,永鼎股份、太辰光涨超5%,天孚通讯涨逾4%。 消息面上,光通讯闻名咨询机构LightCounting近日发布的202…...
【蓝桥杯】[递归]母牛的故事
原题链接:https://www.dotcpp.com/oj/problem1004.html 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 我们列一个年份和母牛数量的表格: 通过观察,找规律,我们发现: 当年份小于等于4时&…...
使用RDP可视化远程桌面连接Linux系统
使用RDP可视化远程桌面连接Linux系统 远程桌面连接Linux安装安装包准备服务器安装xrdp远程连接 远程桌面连接Linux 通常使用SSH来连接服务器,进行命令行操作,但是这次需要远程调试生产环境的内网服务器,进行浏览器访问内网网站,至…...
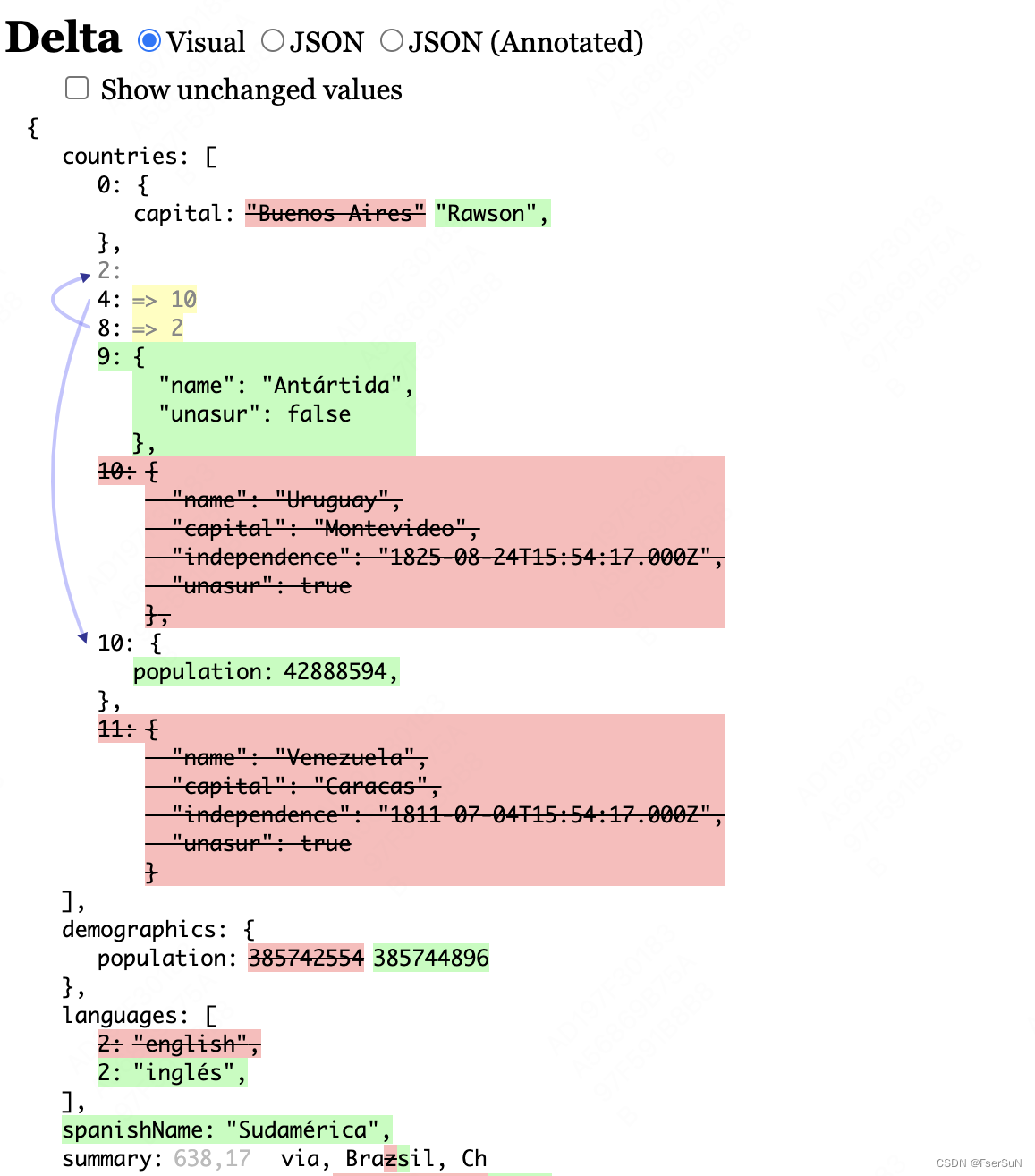
数据可视化diff工具jsondiffpatch使用学习
1.jsondiffpatch 简介 jsondiffpatch 是一个用于比较和生成 JSON 数据差异的 JavaScript 库。它可以将两个 JSON 对象进行比较,并生成一个描述它们之间差异的 JSON 对象。这个差异对象可以用于多种用途,例如: 生成可视化的差异报告应用差异…...
pdf 转 word
pdf 转 word 一、思路 直接调用LibreOffice 命令进行文档转换的命令行工具 使用的前系统中必须已经安装了 libreofficelibreoffice已翻译的用户界面语言包: 中文 (简体)libreoffice离线帮助文档: 中文 (简体)上传字体 重点:重点:重点: 亲…...
【数据结构OJ题】设计循环队列
原题链接:https://leetcode.cn/problems/design-circular-queue/ 1. 题目描述 2. 循环队列的概念和结构 为充分利用向量空间,克服"假溢出"现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。…...

Java 中创建对象有哪些方式?
目录 面试回答 使用 new 关键字 使用反射机制 使用 Class 类的 newInstance() 方法 使用 Constructor 类的 newInstance 方法 使用 clone 方法 使用反序列化 使用方法句柄 使用 Unsafe 分配内存 面试回答 使用 new 关键字 这是我们最常用的、也是最简单的创建对象的方…...

Kafka 消息发送和消费流程
发送消息 流程如下: Producer 端直接将消息发送到 Broker 中的 Leader 分区中Broker 对应的 Leader 分区收到消息会先写入 Page Cache,定时刷盘进行持久化(顺序写入磁盘)Follower 分区拉取 Leader 分区的消息,并保持…...
)
UVa10048 Audiophobia(floyd)
题意 给出一个图,图中的边表示从点u到点v路径上的噪音。给出q个查询,问从u到v所经路径上的最小噪音 思路 在使用floyd计算点对之间的路径时, D u , v k m i n { D u , v k − 1 , m a x { D u , k k − 1 , D k , v k − 1 } } D_{u, v}^…...
Redis概述
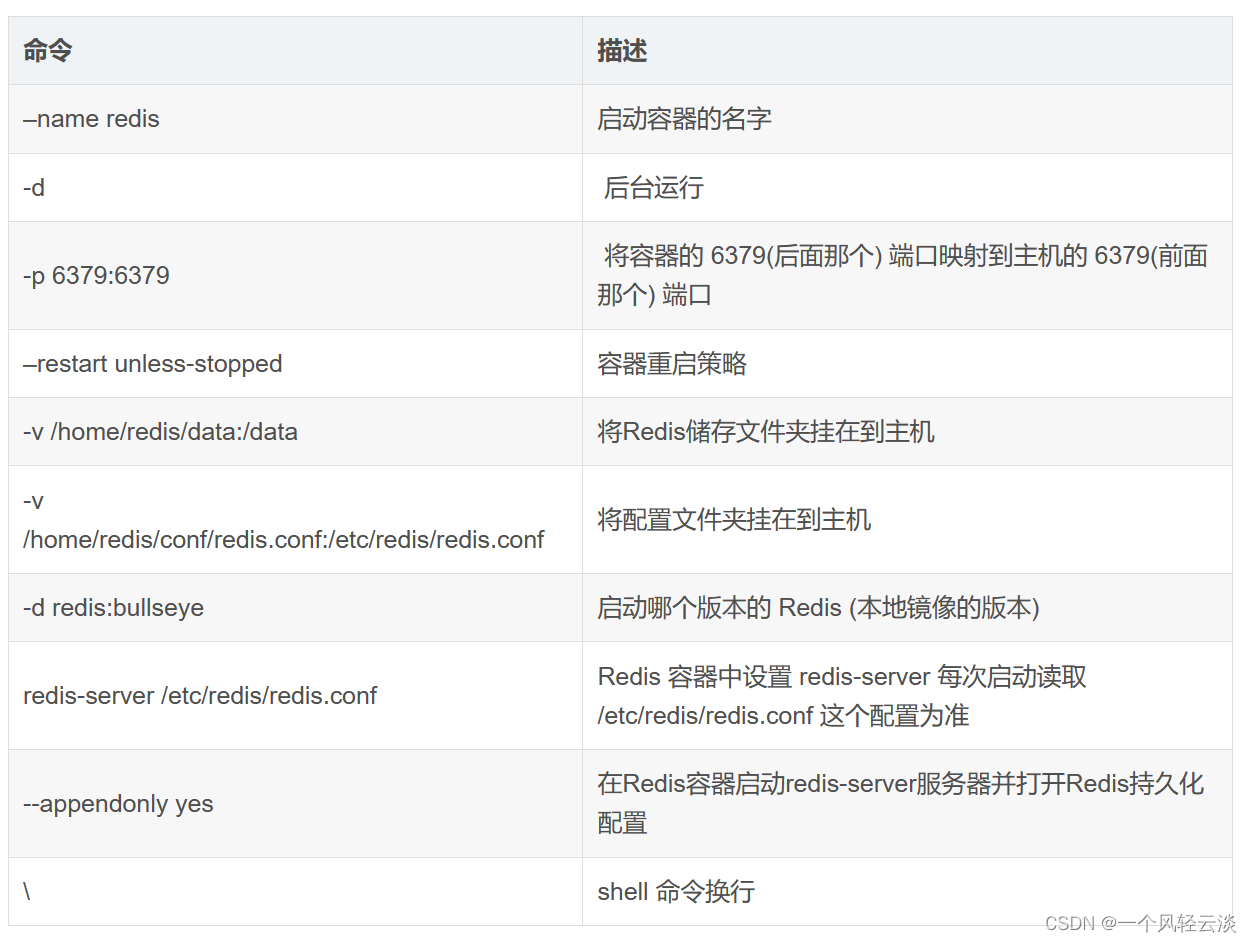
目录 Redis - 概述 使用场景 如何安装 Window 下安装 Linux 下安装 docker直接进行安装 下载Redis镜像 Redis启动检查常用命令 Redis - 概述 redis是一款高性能的开源NOSQL系列的非关系型数据库,Redis是用C语言开发的一个开源的高键值对(key value)数据库,官方提供测试…...

MsrayPlus多功能搜索引擎采集软件
MsrayPlus多功能搜索引擎采集软件 摘要: 本文介绍了一款多功能搜索引擎软件-MsrayPlus,该软件能够根据关键词从搜索引擎中检索相关数据,并提供搜索引擎任务、爬虫引擎任务和联系信息采集三大功能。我们将分析该软件在不同领域的应用…...

机器学习之概率论
最近,在了解机器学习相关的数学知识,包括线性代数和概率论的知识,今天,回顾了概率论的知识,贴上几张其他博客的关于概率论的图片,记录学习过程。...

【深度学习 | 数据可视化】 视觉展示分类边界: Perceptron模型可视化iris数据集的决策边界
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
【计算机视觉】相机基本知识(还在更新)
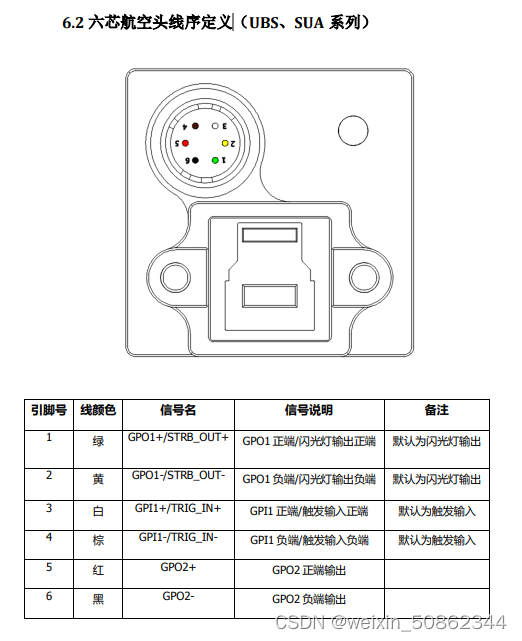
1.面阵工业相机与线阵工业相机 1.1 基本概念区别 面阵相机则主要采用的连续的、面状扫描光线来实现产品的检测; 线阵相机即利用单束扫描光来进行物体扫描的工作的。 1.2 优缺点 (1)面阵CCD工业相机: 优点:应用面…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
