问题记录：mac系统偏好设置不展示mysql
Mac新系统升级（10.14.5）后未从appstore下载的软件在安装时会提示安装包已损坏之类的东东，这是因为没有打开“设置”—“安全与隐私”中的“任何来源”造成的，可是升级后的10.14.5却没有这个选项。
那么macOS 10.14.5以上允许任何来源没有了怎么办？macOS 10.14.5允许任何来源没了怎么开启？
打开终端输入：sudo spctl --master-disable
安装流程：
在Mac上安装mysql数据库_Pansanday的博客-CSDN博客
相关文章：
问题记录：mac系统偏好设置不展示mysql
Mac新系统升级（10.14.5）后未从appstore下载的软件在安装时会提示安装包已损坏之类的东东，这是因为没有打开“设置”—“安全与隐私”中的“任何来源”造成的，可是升级后的10.14.5却没有这个选项。 那么macOS 10.14.5以上允许任何…...
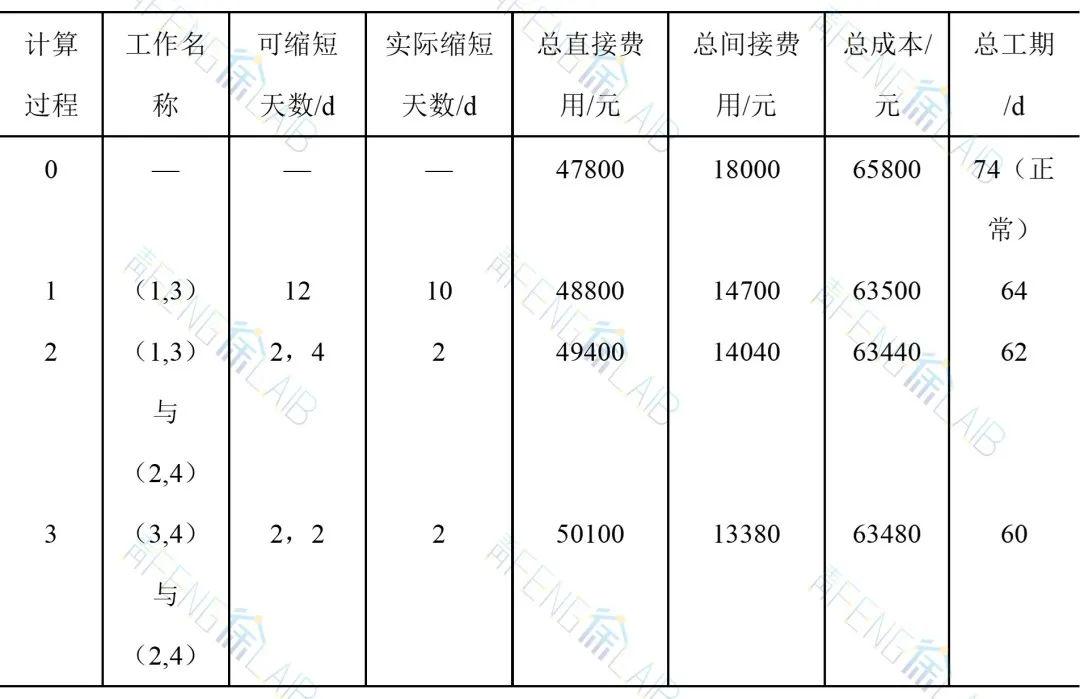
网络计划--时间参数的计算和优化
根据网络图的基本概念和原则绘制出网络图之后，我们可以计算网络图中有关的时间参数，主要目的是找出关键路线，为网络计划的优化、调整和执行提供明确的时间概念。如下图中从始点①到终点⑧共有4条路线，可以分别计算出每条路线所需的…...
1.2.7存储结构-磁盘管理：磁盘移臂调度算法、先来先服务（FCFS）、最短寻道时间优先（SSTF）、扫描算法（SCAN）、循环扫描（CSCAN）
1.2.7存储结构-磁盘管理：磁盘移臂调度算法、先来先服务（FCFS）、最短寻道时间优先（SSTF）、扫描算法（SCAN）、循环扫描（CSCAN）先来先服务（FCFS）最短寻…...
2022年AI顶级论文 —生成模型之年（上）
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 过去十年来，人工智能技术在持续提高和飞速发展，并不断冲击着人类的认知。 2012年，在ImageNet图像识别挑战赛中，一种神经网络模型（AlexNet&…...
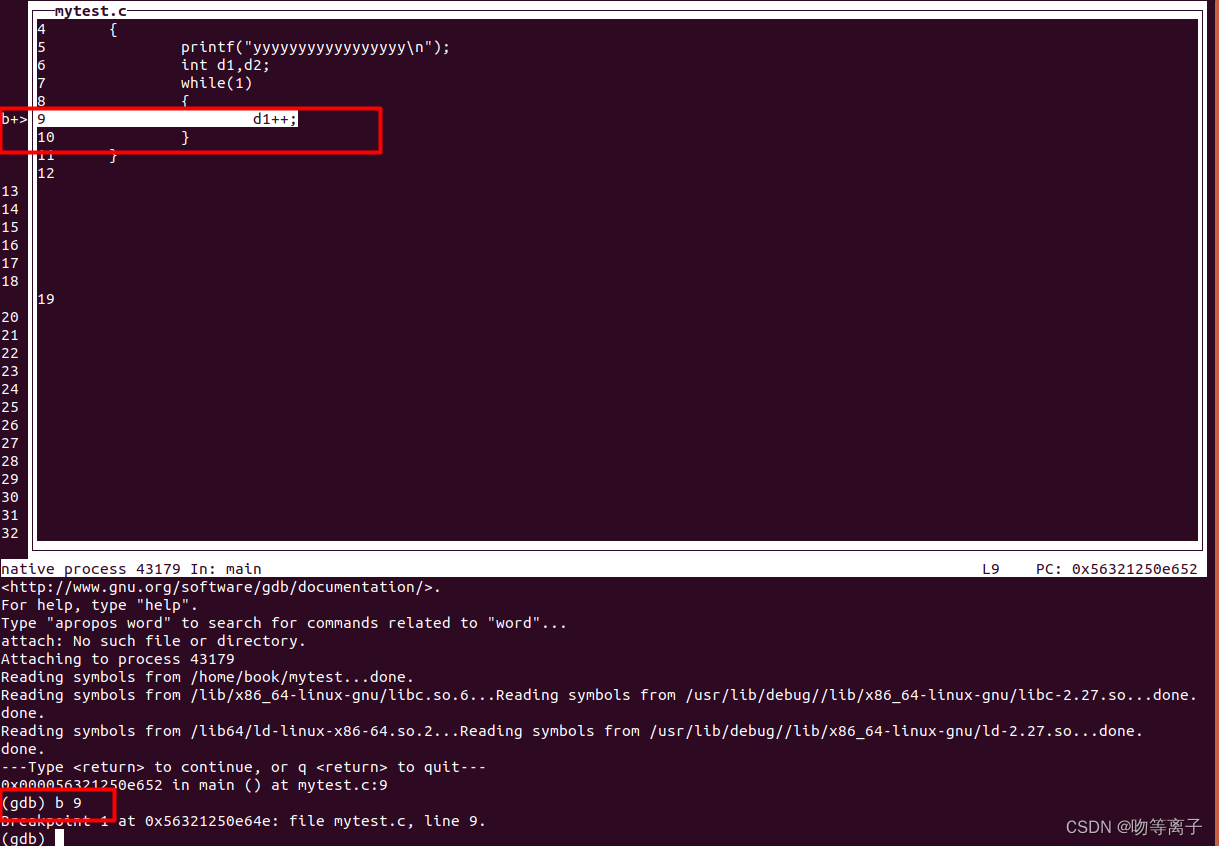
Linux下程序调试的方法【GDB】GDB相关命令和基础操作（命令收藏）
目录 1、编译 2、启动gdb调试 2.1 直接运行 2.2 运行gdb后使用run命令 2.3 调试已运行的程序 3、图形界面提示 4、调试命令 1、查看源码 2、运⾏程序/查看运⾏信息 3、设置断点 5、单步/跳步执⾏ 6、分割窗口 7、其他命令 8、相关参数 1、编译 在编译时要加上-g选…...
使用frp配置内网机器访问
frp简介 frp 是一个开源、简洁易用、高性能的内网穿透和反向代理软件，支持 tcp, udp, http, https等协议。frp 项目官网是 https://github.com/fatedier/frp，软件下载地址为https://github.com/fatedier/frp/releases frp工作原理 服务端运行…...
简述7个流行的强化学习算法及代码实现！
目前流行的强化学习算法包括 Q-learning、SARSA、DDPG、A2C、PPO、DQN 和 TRPO。这些算法已被用于在游戏、机器人和决策制定等各种应用中，并且这些流行的算法还在不断发展和改进，本文我们将对其做一个简单的介绍。1、Q-learningQ-learning：Q-…...
朗润国际期货招商：地方政府工作报告中对于促进消费
地方政府工作报告中对于促进消费 北京：把恢复和扩大消费摆在优先位置。加紧推进国际消费中心城市建设、深化商圈改造提升行动、统筹推进物流基地规划建设，强化新消费地标载体建设、试点建设80个“一刻钟便民生活圈”，提高生活性服务重品质。…...
前端性能优化的一些技巧(90% chatGpt生成)
终于弄好了chatGpt的账号，赶紧来体验一波。先来一波结论，这篇文章的主要内容来源，90%是用chatGpt生成的。先上chatGpt的生成的结果：作为一名懒惰的程序员，chatGpt会帮助我变得更懒...，好了下面开始文章的正…...
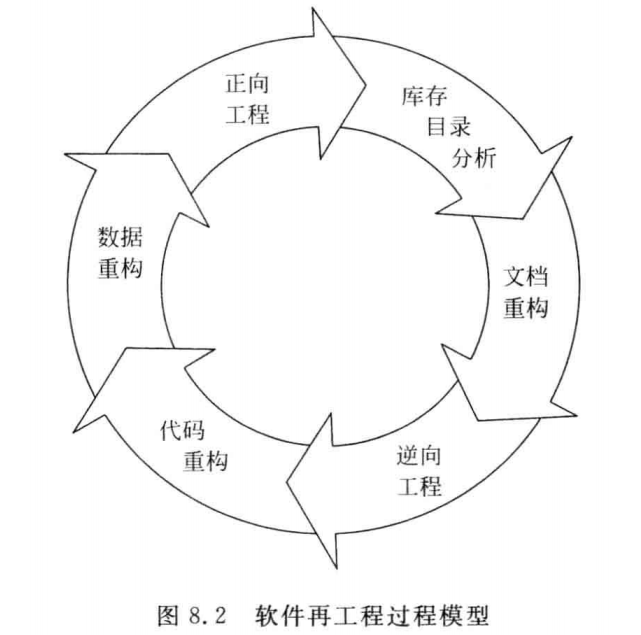
[软件工程导论(第六版)]第8章 维护（复习笔记）
文章目录8.1 软件维护的定义8.2 软件维护的特点8.3 软件维护过程8.4 软件的可维护性8.5 预防性维护8.6 软件再工程过程维护的基本任务：保证软件在一个相当长的时期能够正常运行软件工程的主要目的就是要提高软件的可维护性，减少软件维护所需要的工作量&a…...
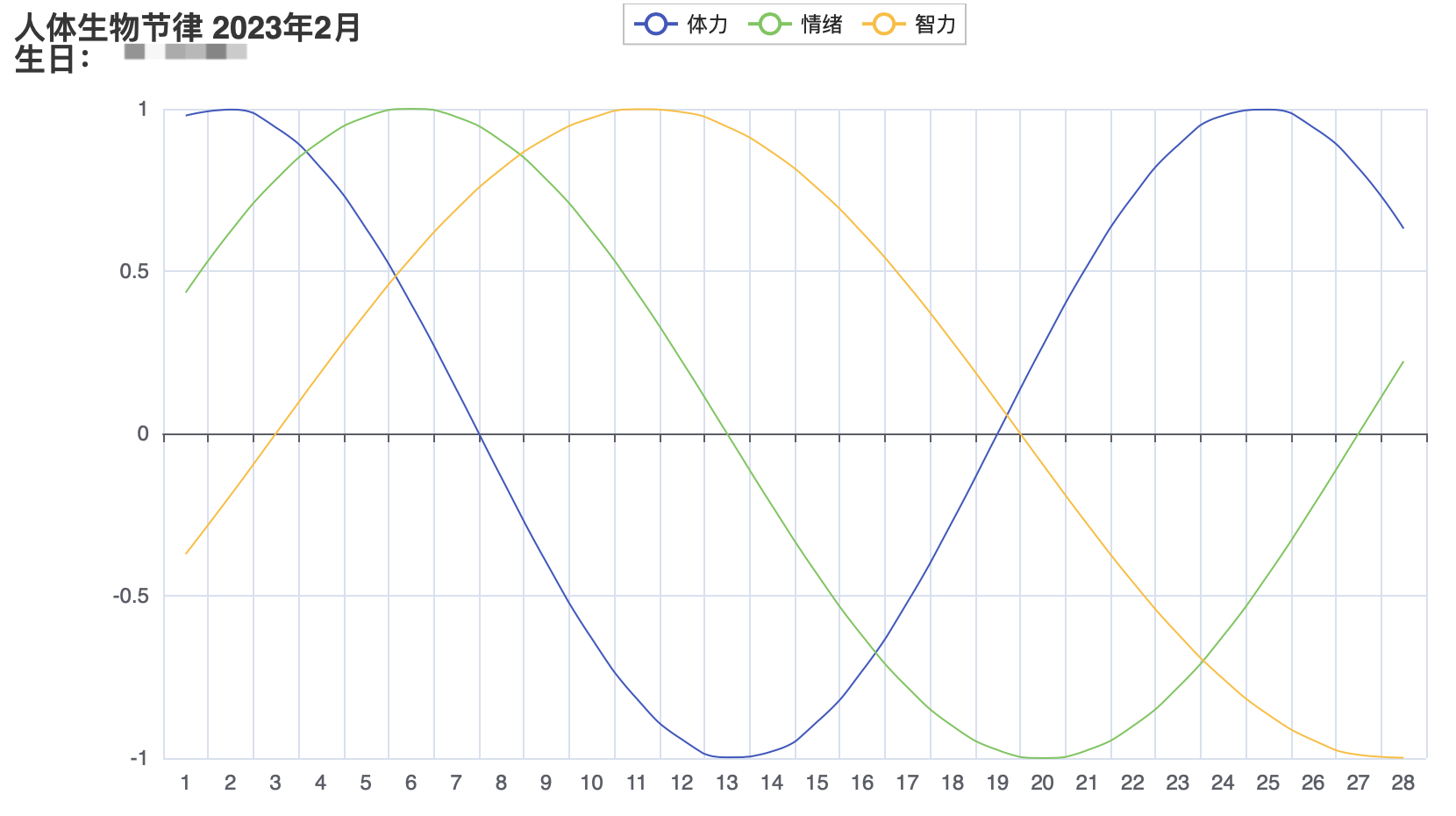
Python - 绘制人体生物节律
文章目录项目说明关于人体生物节律用到的技术代码实现获取每月有多少天计算每天到生日过了多少天计算节律绘图结果项目说明 这里仿照 http://www.4qx.net/The_Human_Body_Clock.php 做一个人体生物节律的计算和展示 关于人体生物节律 百度/维基百科 解释 https://zh.wikiped…...
【NVMEM子系统】二、NVMEM驱动框架
个人主页：董哥聊技术我是董哥，嵌入式领域新星创作者创作理念：专注分享高质量嵌入式文章，让大家读有所得！文章目录1、前言2、驱动框架3、源码目录结构4、用户空间下的目录结构1、前言 NVMEM SUBSYSTEM，该子系…...
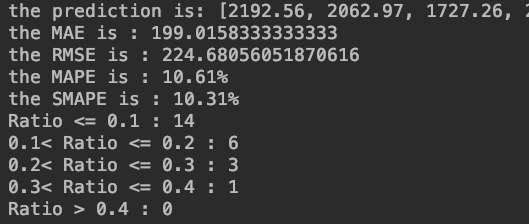
小波神经网络（WNN）的实现（Python，附源码及数据集）
文章目录一、理论基础1、小波神经网络结构2、前向传播过程3、反向传播过程4、建模步骤二、小波神经网络的实现1、训练过程（WNN.py）2、测试过程（test.py）3、测试结果4、参考源码及实验数据集一、理论基础 小波神经网络（…...
商标干货！所有企业都值得收藏！
商标，是用于识别和区分不同商品或服务来源的标志，代表了企业的产品质量和服务保证，可以说，商标承载了一个企业的信誉，是企业参与市场竞争的重要工具，对于企业及其产品的重要性不言而喻。 根据《商标法》四十…...
4次迭代，让我的 Client 优化 100倍！泄漏一个 人人可用的极品方案！
4次迭代，让我的HttpClient提速100倍 在大家的生产项目中，经常需要通过Client组件（HttpClient/OkHttp/JDK Connection)调用第三方接口。 尼恩的一个生产项目也不例外。 在一个高并发的中台生产项目中。有一个比较特殊的请求，一次…...
并查集(高级数据结构)-蓝桥杯
一、并查集并查集(Disioint Set)：一种非常精巧而实用的数据结构用于处理不相交集合的合并问题。用于处理不相交集合的合并问题。经典应用：连通子图。最小生成树Kruskal算法。最近公共祖先。二、应用场景有n个人，他们属于不同的帮派。 已知这些…...
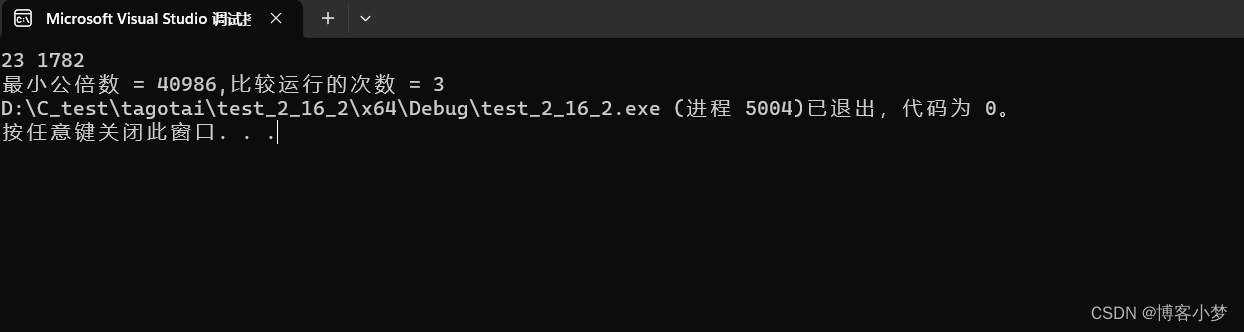
你是真的“C”——C语言详解求两个正数最小公倍数的3种境界
C语言详解求两个正数最小公倍数的3种境界~😎前言🙌必备小知识~😘求最小公倍数境界1~ 😊求最小公倍数境界2~ 😊求最小公倍数境界3~ 😊总结撒花💞博客昵称：博客小梦😊 最喜…...
【java】Spring Cloud --Feign Client超时时间配置以及单独给某接口设置超时时间方法
文章目录feign配置（最常用）ribbon配置hystrix配置单独给某接口设置超时时间FeignClient面对服务级有三种超时时间配置feign配置（最常用） feign:sentinel:enabled: trueclient:config:default://全部服务配置connectTimeout: 5000…...
spark代码
RDD Tom,DataBase,80 Tom,Algorithm,50 Tom,DataStructure,60 Jim,DataBase,90 Jim,Algorithm,60 Jim,DataStructure,80 该系总共有多少学生； val lines sc.textFile("file:///usr/local/spark/sparksqldata/Data01.txt") val par lines.map(ro…...
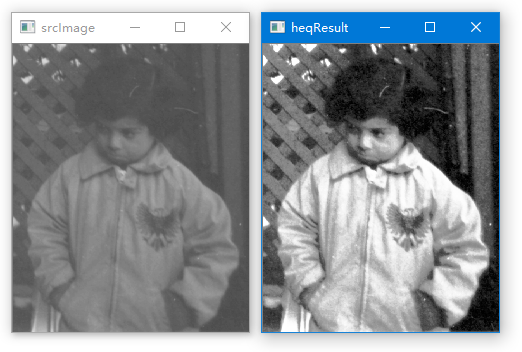
利用OpenCV的函数equalizeHist()对图像作直方图均衡化处理
如果一幅图像的灰度值集中在某个比较窄的区域，则图像的对比度会显得比较小，不便于对图像的分析和处理。 图像的直方图均衡化可以实现将原图像的灰度值范围扩大，这样图像的对比度就得到了提高，从而方便对图像进行后续的分析和处理…...
利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
[特殊字符] 智能合约中的数据是如何在区块链中保持一致的？
🧠 智能合约中的数据是如何在区块链中保持一致的？ 为什么所有区块链节点都能得出相同结果？合约调用这么复杂，状态真能保持一致吗？本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...
iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘
美国西海岸的夏天，再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至，这不仅是开发者的盛宴，更是全球数亿苹果用户翘首以盼的科技春晚。今年，苹果依旧为我们带来了全家桶式的系统更新，包括 iOS 26、iPadOS 26…...
【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU：如何让RNN变得更聪明？ 在深度学习的世界里，循环神经网络（RNN）以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而，传统RNN存在的一个严重问题——梯度消失&#…...
今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售，主打更强图形性能与沉浸式体验，支持多模态交互，受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
如何理解 IP 数据报中的 TTL？
目录 前言理解 前言 面试灵魂一问：说说对 IP 数据报中 TTL 的理解？我们都知道，IP 数据报由首部和数据两部分组成，首部又分为两部分：固定部分和可变部分，共占 20 字节，而即将讨论的 TTL 就位于首…...
Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中，CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时，通常会导致应用响应缓慢，甚至服务不可用，严重影响用户体验和业务运行。因此，掌握一套科学有效的CPU飙高问题排查方法&…...
保姆级教程：在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama（有网络的电脑）2.2.3 安装Ollama（无网络的电脑）2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...