固定值电阻的检测方法总结
相关文章：
固定值电阻的检测方法总结
🏡《总目录》 目录 1，概述2，测量方法3，检测方法3.1，读值3.2，测量3.3，排故4，总结1，概述 本文简单总结固定值电阻的测量与检查方法要点和注意事项。 2，测量方法 对于固定值电阻的测量来讲，直接将万用表红黑表笔分别插入到如下图所示的红色和黑色接线端。然后将万用表…...
打印机相关
打印机相关 打印机协议 ipp，printer-job-language，lpd协议。他们的默认端口分别是631，9100和515. printer-job-language（RAW协议） 9100端口的printer-job-language，又称为RAW协议。目前遇到的问题是，此端口发送数据，打印机直接打印，除非发送正确的printer-job-lan…...
入门力扣自学笔记235 C++ （题目编号：2347）
2347. 最好的扑克手牌 题目： 给你一个整数数组 ranks 和一个字符数组 suit 。你有 5 张扑克牌，第 i 张牌大小为 ranks[i] ，花色为 suits[i] 。 下述是从好到坏你可能持有的 手牌类型 ： "Flush"：同花&…...
k8s-二进制部署
文章目录一、环境二、步骤1、安装cfssl工具2、部署etcd集群3、在node节点安装docker组件4、安装flannel组件部署master节点组件部署node节点部署kube-proxy组件三、测试一、环境 角色服务器地址组件master192.168.174.140kube-apiserver，kube-controller-manager&a…...
前缀和差分（C/C++）
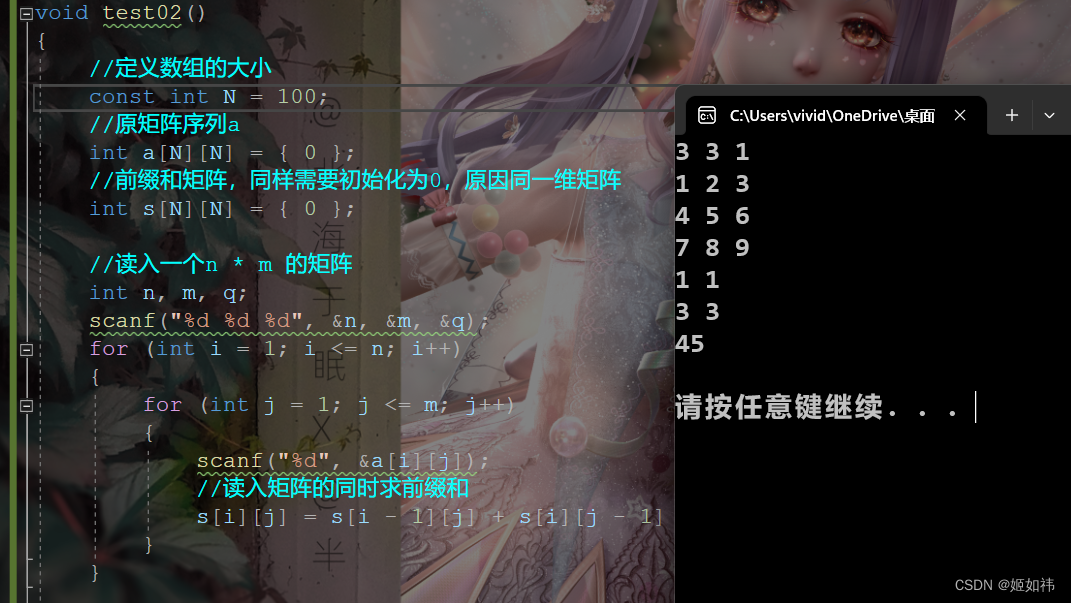
目录 1. 前缀和的定义 2. 一维前缀和 2.1 计算公式 2.2 用途 2.3 小试牛刀 3. 二维前缀和 3.1 用途 1. 前缀和的定义 对于一个给定的数列A，他的前缀和数中 S 中 S[ i ] 表示从第一个元素到第 i 个元素的总和。 如下图：绿色区域的和就是前缀和数组…...
回文子串的数量[寻找回文子串的完整思路过程]
寻找回文子串的完整思路过程前言一、回文串的数量二、动态规划1、完整思考过程2、go总结参考文献前言 回文字符串，就是从左遍历和从右遍历的字符是相同顺序的，转换一下，就是该字符串是对称的。寻找回文子串面临两个直接的问题，1-…...
CCNP350-401学习笔记（301-350题）
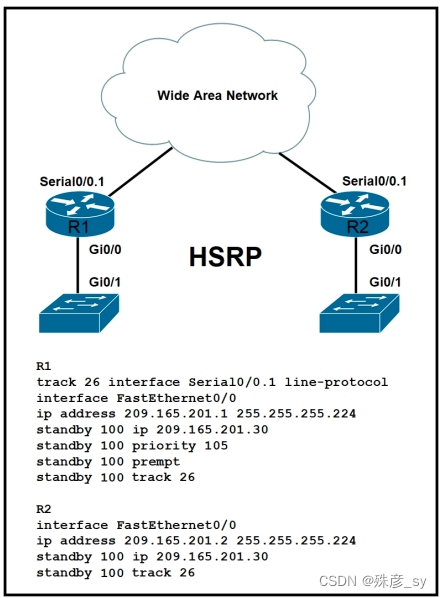
301、Drag and drop the virtual component from the left onto their descriptions on the right. 302、Which two actions, when applied in the LAN network segment, will facilitate Layer 3 CAPWAP discovery for lightweight AP? (Choose two.)A. Utilize DHCP option …...
【LeetCode】No.225. 用队列实现栈 -- Java Version
题目链接：https://leetcode.cn/problems/implement-stack-using-queues/ 1. 题目介绍（225. 用队列实现栈） 请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、t…...
45个写规范代码的小技巧
目录 1、规范命名 2、规范代码格式 3、写好代码注释 4、try catch 内部代码抽成一个方法 5、方法别太长 6、抽取重复代码 7、多用return 8、if条件表达式不要太复杂 9、优雅地参数校验 10、统一返回值 11、统一异常处理 12、尽量不传递null值 13、尽量不返回null值…...
MindFusion Diagramming for Java, 最新版 Crack
Diagramming for Java, V4.6.1 A unique Java Swing library for any type of flowchart.您需要的每一个图表功能 图表、方案、图形、网络、算法、树、图表 - 所有这些都是使用 MindFusion Diagramming for Java 工具快速轻松地构建的。结果令人着迷。 Java Dagram 库ÿ…...
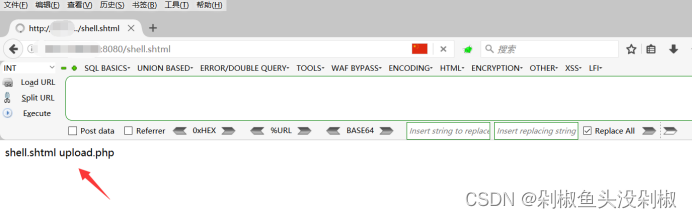
中间件安全—Apache常见漏洞
中间件安全—Apache常见漏洞1.Apache常见漏洞1.1.Apache介绍1.2.Apache HTTPD 换行解析漏洞（CVE-2017-15715）1.2.1.漏洞介绍1.2.2.漏洞环境1.2.2.1.运行漏洞环境1.2.2.2.访问漏洞环境1.2.3.漏洞复现1.2.3.1.拦截1.2.3.2.添加换行1.2.3.3.访问文件1.3.Apa…...
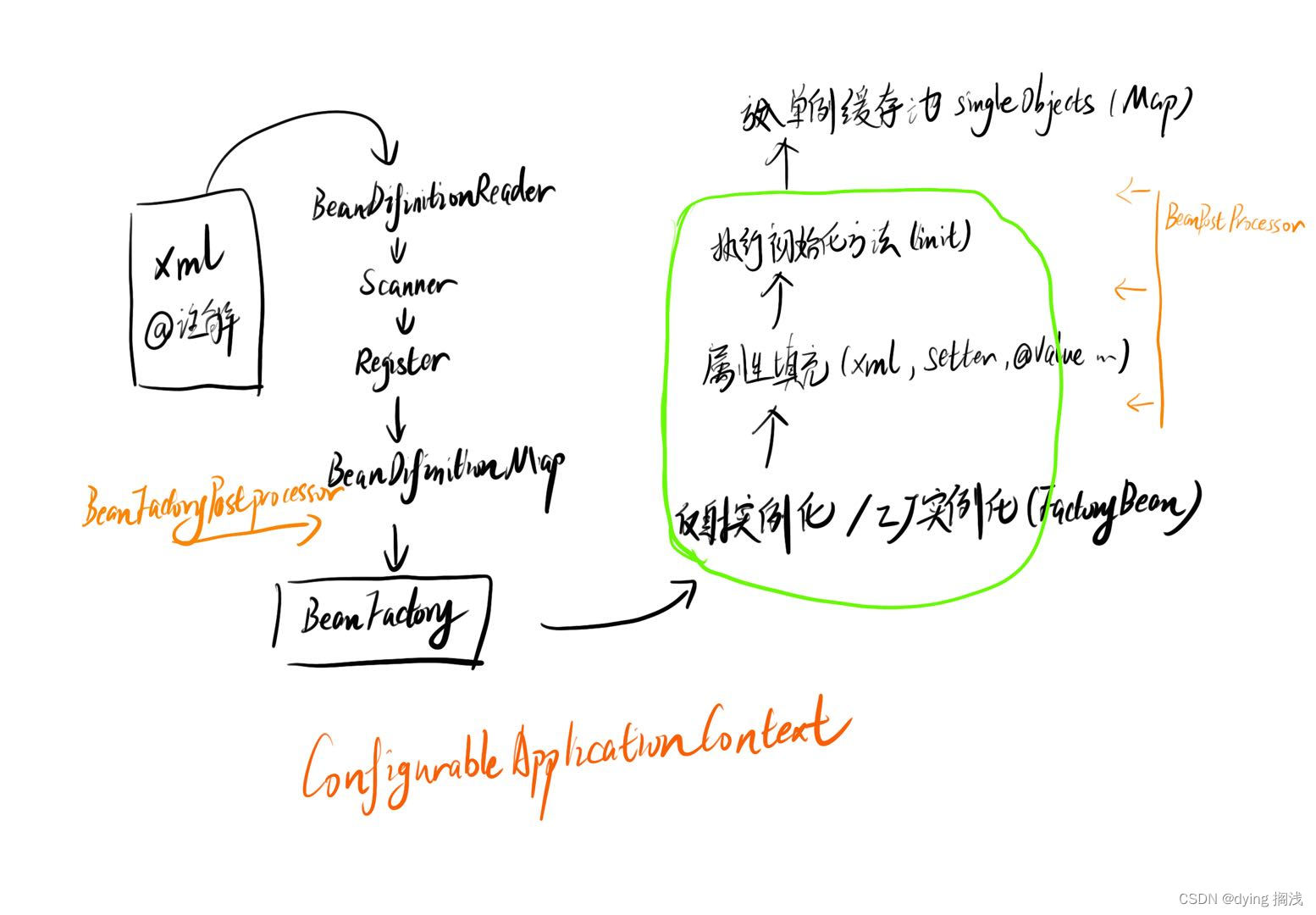
Spring IOC 容器 Bean 加载过程
Spring IOC 容器 Bean 加载过程 Spring 对于我们所有的类对象进行了统一抽象，抽象为 BeanDefinition ，即 Bean 的定义，其中定义了类的全限定类名、加载机制、初始化方式、作用域等信息，用于对我们要自动装配的类进行生成。 Sprin…...
【DRF】Django Rest Framework（5.DRF中的通用视图类-GenericAPIView方法说明与使用说明）
1. GenericAPIView [通用视图类]，概述 继承自 APIView增加了操作序列化器和数据库查询的方法，作用是为下面Mixin扩展类的执行提供方法支持。通常在使用时，可搭配一个或者多个Mixin扩展类源码 当我们查看 GenericAPIView 的源码时，…...
STM32 OTA应用开发——自制BootLoader
STM32 OTA应用开发——自制BootLoader 目录STM32 OTA应用开发——自制BootLoader前言1 环境搭建2 BootLoader工作原理以及常见分区介绍3 BootLoader的制作4 烧录下载配置5 运行测试结束语前言 什么是OTA？ 百度百科：空中下载技术（Over-the-Ai…...
时域和频域的简单理解
目录文章背景结论举例说明说回频域连续或离散总结文章背景 时域和频域在傅里叶变换和拉普拉斯变换，z变换中经常提到的高频词。本文的重点就是想说明怎么理解 “频域” 这个名词。 结论 频域就是一个信号 所有组成频率的取值范围的集合 举例说明 以大家从中小学开…...
华为OD机试 - 第 K 个最小码值的字母 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法（Python） | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号（JavaScript） 华为OD机试 - 猜字谜（Python） | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录（Python） | 机试题算法思路 【2023】 华为OD机试 …...
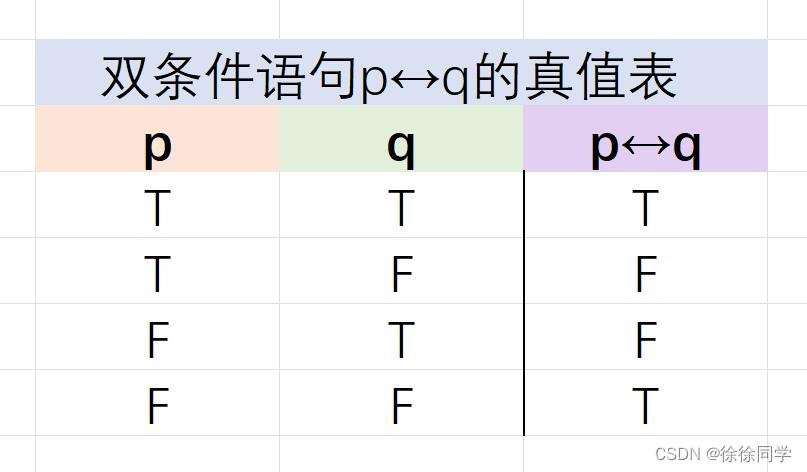
离散数学笔记_第一章：逻辑和证明（1）
1.1命题逻辑1.1.1 命题 1.1.2 逻辑运算符 定义1： 否定联结词定义2： 合取联结词定义3： 析取联结词定义4： 异或联结词1.1.3 条件语句 定义5： 条件语句定义6： 双条件语句1.1.1 命题 1.命题：是…...
Rust FFI 与C语言互相调用
参考 https://cloud.tencent.com/developer/article/2077534 https://github.com/shepmaster/rust-ffi-omnibus cbindgen 简介 二进制方式构建 $ cargo install cbindgen //默认构建C头文件 C语言需要 --lang C $ cd /path/to/my/project && cbindgen . -o target/…...
从全局变量寻找到Tomcat回显方式
前言 对于回显的获取主要是在ApplicationFilterChain类的lastServicedRequest / lastServicedResponse两个属性，是使用的ThreadLocal进行修饰的，并且，在执行请求的过程中，通过反射修改属性值，能够记录下当前线程的req…...
Tapdata Connector 实用指南：数据入仓场景之数据实时同步到 BigQuery
【前言】作为中国的 “Fivetran/Airbyte”, Tapdata 是一个以低延迟数据移动为核心优势构建的现代数据平台，内置 60 数据连接器，拥有稳定的实时采集和传输能力、秒级响应的数据实时计算能力、稳定易用的数据实时服务能力，以及低代码可视化操作…...
多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言：多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时，基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套：跨云网络构建数据…...
Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接：3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...
React Native 开发环境搭建（全平台详解）
React Native 开发环境搭建（全平台详解） 在开始使用 React Native 开发移动应用之前，正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南，涵盖 macOS 和 Windows 平台的配置步骤，如何在 Android 和 iOS…...
DeepSeek 技术赋能无人农场协同作业：用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
均衡后的SNRSINR
本文主要摘自参考文献中的前两篇，相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程，其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线， n r n_r nr 根接收天线的 MIMO 系…...
Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型（算法、数据分析、机器学习等）不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
6个月Python学习计划 Day 16 - 面向对象编程（OOP）基础
第三周 Day 3 🎯 今日目标 理解类（class）和对象（object）的关系学会定义类的属性、方法和构造函数（init）掌握对象的创建与使用初识封装、继承和多态的基本概念（预告） &a…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益（IG） 分类器设计贝叶斯理论：线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别， 有单标签多类别文本分类和多…...
使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件，这个上传文件是整体功能的一部分，文件在上传的过程中…...