【力扣周赛】第360场周赛
【力扣周赛】第360场周赛
- 8015.距离原点最远的点
- 题目描述
- 解题思路
- 8022. 找出美丽数组的最小和
- 题目描述
- 解题思路
8015.距离原点最远的点
题目描述
描述:给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘_’ 组成。字符串表示你在一条原点为 0 的数轴上的若干次移动。
你的初始位置就在原点(0),第 i 次移动过程中,你可以根据对应字符选择移动方向:
如果 moves[i] = ‘L’ 或 moves[i] = ‘’ ,可以选择向左移动一个单位距离
如果 moves[i] = ‘R’ 或 moves[i] = '’ ,可以选择向右移动一个单位距离
移动 n 次之后,请你找出可以到达的距离原点 最远 的点,并返回 从原点到这一点的距离 。
示例 1:
输入:moves = "L_RL__R"
输出:3
解释:可以到达的距离原点 0 最远的点是 -3 ,移动的序列为 "LLRLLLR" 。
示例 2:
输入:moves = "_R__LL_"
输出:5
解释:可以到达的距离原点 0 最远的点是 -5 ,移动的序列为 "LRLLLLL" 。
示例 3:
输入:moves = "_______"
输出:7
解释:可以到达的距离原点 0 最远的点是 7 ,移动的序列为 "RRRRRRR" 。
提示:
1 <= moves.length == n <= 50
moves 仅由字符 ‘L’、‘R’ 和 ‘_’ 组成
解题思路
思路:脑筋急转弯,将直观模拟转换为求解L和R数量,因为L和R可以抵消,故可以将_转换为L和R较多的那个再进行求解。
class Solution {
public:int furthestDistanceFromOrigin(string moves) {int n=moves.size();// l表示L数量 r表示R数量int l=0,r=0;// 转化为l与r抵消剩余多少则往哪个方向移动for(auto move:moves){if(move=='R')r++;if(move=='L')l++;}return l>r?n-2*r:n-2*l;}
};
总结:首先是理解题意,然后是直观模拟,当直观模拟较为复杂,则考虑在不改变结果的情况下如何转换求解以便优化时空复杂度。
8022. 找出美丽数组的最小和
题目描述
描述:给你两个正整数:n 和 target 。
如果数组 nums 满足下述条件,则称其为 美丽数组 。
nums.length == n.
nums 由两两互不相同的正整数组成。
在范围 [0, n-1] 内,不存在 两个 不同 下标 i 和 j ,使得 nums[i] + nums[j] == target 。
返回符合条件的美丽数组所可能具备的 最小 和。
示例 1:
输入:n = 2, target = 3
输出:4
解释:nums = [1,3] 是美丽数组。
- nums 的长度为 n = 2 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ,使得 nums[i] + nums[j] == 3 。
可以证明 4 是符合条件的美丽数组所可能具备的最小和。
示例 2:
输入:n = 3, target = 3
输出:8
解释:
nums = [1,3,4] 是美丽数组。
- nums 的长度为 n = 3 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ,使得 nums[i] + nums[j] == 3 。
可以证明 8 是符合条件的美丽数组所可能具备的最小和。
示例 3:
输入:n = 1, target = 1
输出:1
解释:nums = [1] 是美丽数组。
提示:
1 <= n <= 105
1 <= target <= 105
解题思路
思路:最开始是一种很神奇的感觉,没有说那种脑海中浮现出很直观的清晰的逻辑思路,但是写着写着就写出来了。贪心想法,必定是按照1、2、3…n的顺序得到的数组和最小,而且1必定在结果中,所以使用uset存储已经加入结果集合,初始为1,使用num表示当前加入元素,初始为2,使用res表示当前数组和,初始为1,当在uset中找不到与num相加和为target的元素时则将num加入uset并更新数组和res。
class Solution {
public:long long minimumPossibleSum(int n, int target) {// 长度为1的数组最小为1if(n==1)return 1;// 记录元素和 1肯定在long long res=1;// 记录加入元素unordered_set<int> uset;uset.emplace(1);// 记录当前加入元素int num=2;// 1 2 3 4依次加入最小 按照target排除不能加入元素 使用uset记录已经加入元素while(uset.size()<n){if(uset.find(target-num)==uset.end()){uset.emplace(num);res+=num;}num++;}return res;}
};
优化:当时在模拟示例数据时,想到对于元素和target,在和为target的两两配对中必定选取较小的那个数,而对于大于等于target的数选择部分数使得总数据数量为n。
class Solution {
public:long long minimumPossibleSum(int n, int target) {// 第一部分:两两配对中取较小者 1、2、3...k/2 使得n>=mlong long m=min(target/2,n);// 第二部分:剩余n-m个数 k...k+n-m-1 如果最小m为n 那么后者为0return (m*(m+1)+(target*2+n-m-1)*(n-m))/2;}
};
PS:后两题不会hhh,有时候想想刷题真神奇,因为无论如何都不会到达天花板,总是会在某些题中找到无力感和挫败感,但是又有什么办法呢,感觉还是多总结多思考,不断积累思路,然后形成知识体系,总有一天会blingblingbling的吧~~
相关文章:

【力扣周赛】第360场周赛
【力扣周赛】第360场周赛 8015.距离原点最远的点题目描述解题思路 8022. 找出美丽数组的最小和题目描述解题思路 8015.距离原点最远的点 题目描述 描述:给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘_’ 组成。字符串表示你在…...

php环境变量的配置步骤
要配置PHP的环境变量,以便在命令行中直接使用php命令,以下是一般的步骤: Windows 操作系统 下载和安装PHP:首先,你需要从PHP官方网站(https://www.php.net/downloads.php)下载适用于你的操作系…...

Kdtree
Kdtree kdtree 就是在 n 维空间对数据点进行二分;具体先确定一个根,然后小于在这个维度上的根的节点在左边,大于的在右边,再进行下一个维度的划分。直到维度结束,再重复,或者直到达到了结束条件࿱…...
算法leetcode|74. 搜索二维矩阵(rust重拳出击)
文章目录 74. 搜索二维矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java: 74. 搜索二维矩阵: 给你一个满足下述两条属性的…...

element浅尝辄止7:InfiniteScroll 无限滚动
滚动加载:滚动至底部时,加载更多数据。 1.如何使用? //在要实现滚动加载的列表上上添加v-infinite-scroll,并赋值相应的加载方法, //可实现滚动到底部时自动执行加载方法。<template><ul class"infinit…...

Day05-Vue基础
Day05-Vue基础 一、单向数据流 父子组件通信。会在父组件中定义好数据,将数据传递给子组件,可以使用这个数据 Vue中针对props这个属性提出了一个单向数据流的概念。 Vue针对props做了一些限制,可以接受值,使用这个值,规范中不要去直接修改这个值 目的是为了对数据流进…...
《机器学习在车险定价中的应用》实验报告
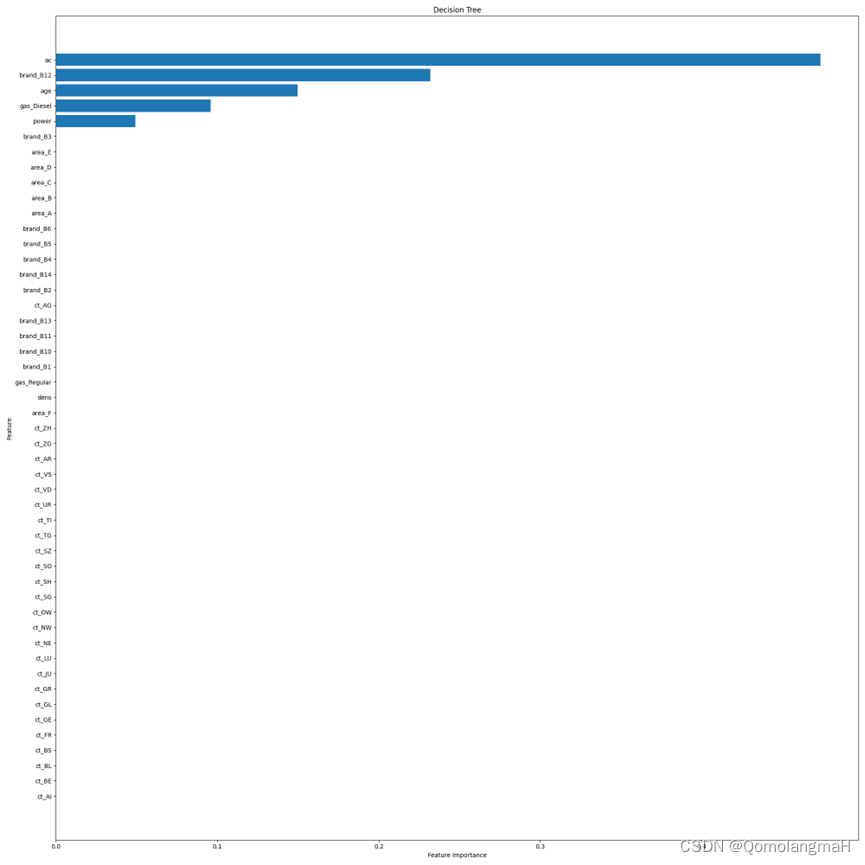
目录 一、实验题目 机器学习在车险定价中的应用 二、实验设置 1. 操作系统: 2. IDE: 3. python: 4. 库: 三、实验内容 实验前的猜想: 四、实验结果 1. 数据预处理及数据划分 独热编码处理结果(以…...
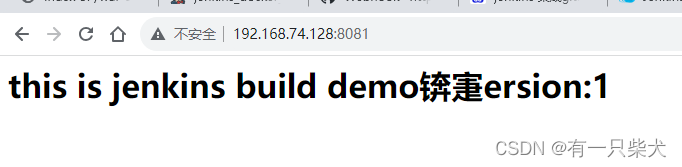
14. Docker中实现CI和CD
目录 1、前言 2、什么是CI/CD 3、部署Jenkins 3.1、下载Jenkins 3.2、启动Jenkins 3.3、访问Jenkins页面 4、Jenkins部署一个应用 5、Jenkins实现Docker应用的持续集成和部署 5.1、创建Dockerfile 5.2、集成Jenkins和Docker 6、小结 1、前言 持续集成(CI/CD)是一种…...

【多思路解决喝汽水问题】1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水
题目内容 喝汽水问题 喝汽水,1瓶汽水1元,2个空瓶可以换一瓶汽水,给20元,可以喝多少汽水(编程实现)。 题目分析 数学思路分析 根据给出的问题和引用内容,我们可以得出答案。 首先ÿ…...
)
P1591 阶乘数码(Java高精度)
题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式 对于每组数据&a…...

Mybatis的动态SQL及关键属性和标识的区别(对SQL更灵活的使用)
( 虽然文章中有大多文本内容,想了解更深需要耐心看完,必定大有受益 ) 目录 一、动态SQL ( 1 ) 是什么 ( 2 ) 作用 ( 3 ) 优点 ( 4 ) 特殊标签 ( 5 ) 演示 二、#和$的区别 2.1 #使用 ( 1 ) #占位符语法 ( 2 ) #优点 2.…...
mysql下载
网址 MySQL :: Download MySQL Community Serverhttps://dev.mysql.com/downloads/mysql/ 2、选择MSI进行安装 3、这里我选择离线安装 4、这里我选择直接下载 5、等待下载安装即可...

聚合函数与窗口函数
聚合函数 回答一 聚合函数(Aggregate Functions)是SQL中的函数,用于对一组数据进行计算,并返回单个结果。聚合函数通常用于统计和汇总数据,包括计算总和、平均值、计数、最大值和最小值等。 以下是一些常见的聚合函…...
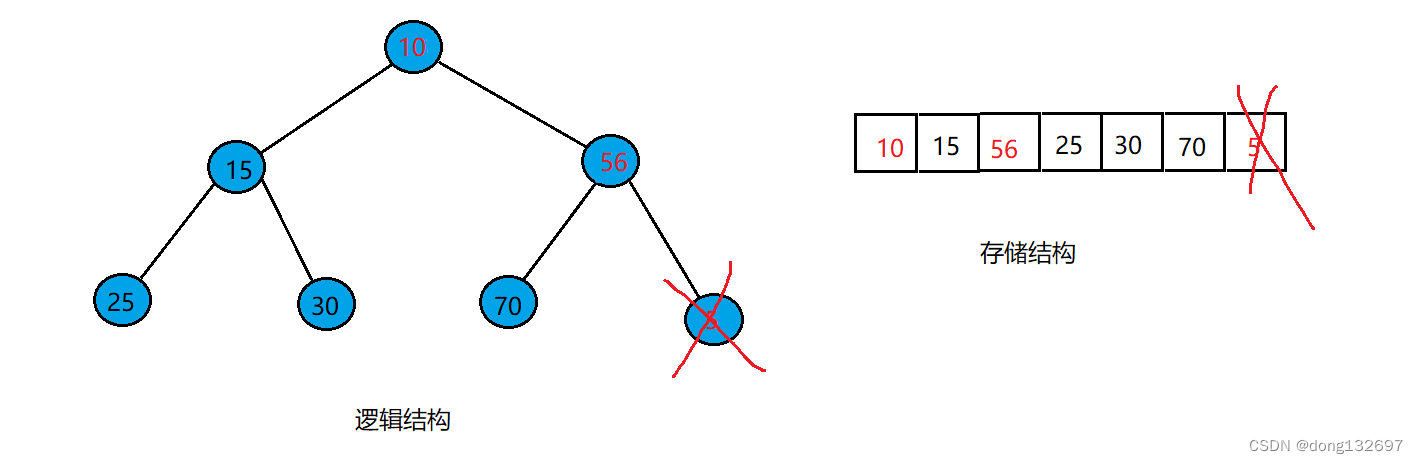
c语言实现堆
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、树1、树的概念2、树的相关概念3、树的表示 二、二叉树1、二叉树概念2、特殊的二叉树3、二叉树的性质4、二叉树的顺序结构5、二叉树的链式结构 三、堆(二叉树…...

ubuntu 如何将文件打包成tar.gz
要将文件打包成.tar.gz文件,可以使用以下命令: tar -czvf 文件名.tar.gz 文件路径 其中,-c表示创建新的归档文件,-z表示使用gzip进行压缩,-v表示显示详细的打包过程,-f表示指定归档文件的名称。 例如&am…...
)
前端优化页面加载速度的方法(持续更新)
提速方法方向 延迟脚本加载 使用 async 属性: 在这种方法中,脚本将在下载完成后立即执行,而不会阻塞其他页面资源的加载和渲染。这适用于那些不依赖于其他脚本和页面内容的脚本,例如分析脚本等。示例如下: html …...

利用SSL证书的SNI特性建立自己的爬虫ip服务器
今天我要和大家分享一个关于自建多域名HTTPS爬虫ip服务器的知识,让你的爬虫ip服务器更加强大!无论是用于数据抓取、反爬虫还是网络调试,自建一个支持多个域名的HTTPS爬虫ip服务器都是非常有价值的。本文将详细介绍如何利用SSL证书的SNI&#…...

HTML和CSS
HTML HTML(Hyper Text Markup Language):超文本语言 超文本:超越了文本的限制,比普通文本更强大。除了文字信息,还可以定义图片、音频、视频等内容。 标记语言:由标签构成的语言 HTML标签都是预定义好的。例如:使用&l…...

C#的IndexOf
在 C# 中,IndexOf 是一个字符串、数组或列表的方法,用于查找指定元素的第一个匹配项的索引。它返回一个整数值,表示匹配项在集合中的位置,如果未找到匹配项,则返回 -1。 IndexOf 方法有多个重载形式,可以根…...

深度学习2.神经网络、机器学习、人工智能
目录 深度学习、神经网络、机器学习、人工智能的关系 大白话解释深度学习 传统机器学习 VS 深度学习 深度学习的优缺点 4种典型的深度学习算法 卷积神经网络 – CNN 循环神经网络 – RNN 生成对抗网络 – GANs 深度强化学习 – RL 总结 深度学习 深度学习、神经网络…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...
