M1 Pro 利用docker 搭建pytho2的开发环境,以vscode连接开发为例
使用 M1 Pro (不支持python2的安装)开发,需要使用 Python 2.7 的环境,在使用 pyenv 安装 Python 2 时遇到了各种奇怪的问题。最终,我决定使用 Docker 搭建开发环境,并使用 VS Code 连接到本地容器。以下是详细的步骤总结(Markdown 格式):
-
安装 Docker:首先,确保已在 M1 Pro 上安装了 Docker。可以从 Docker 官方网站下载并按照说明进行安装。
-
到DockerHub 获取合适的python版本,以下以
python 2.718为例。
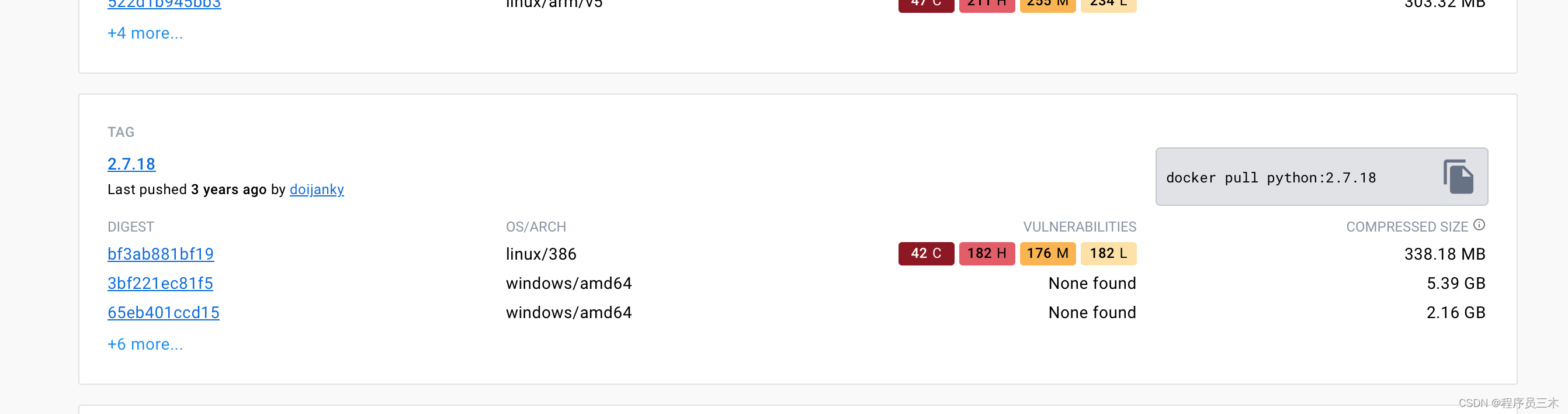
-
创建 Dockerfile:在项目根目录下创建一个名为
Dockerfile的文件。python:2.7.18# 设置工作目录 WORKDIR /app# 复制项目文件到容器中 COPY . /app# 设置环境变量 ENV PYTHONPATH=/app在 Dockerfile 中,我们使用 Python 2.7.18 的官方镜像作为基础镜像,并设置了工作目录、复制项目文件和安装依赖。
-
构建 Docker 镜像:在终端中,进入到包含 Dockerfile 的项目根目录,并运行以下命令来构建 Docker 镜像。
docker build -t my-python2-app .这将根据 Dockerfile 中的配置构建一个名为
my-python2-app的镜像。注意,命令最后的.表示使用当前目录作为构建上下文。 -
运行 Docker 容器:在终端中,运行以下命令来启动一个基于你构建的镜像的 Docker 容器。
docker run -it --rm -v .:/app my-python2-app这将启动一个交互式的容器,并将当前目录挂载到容器的
/app目录中。
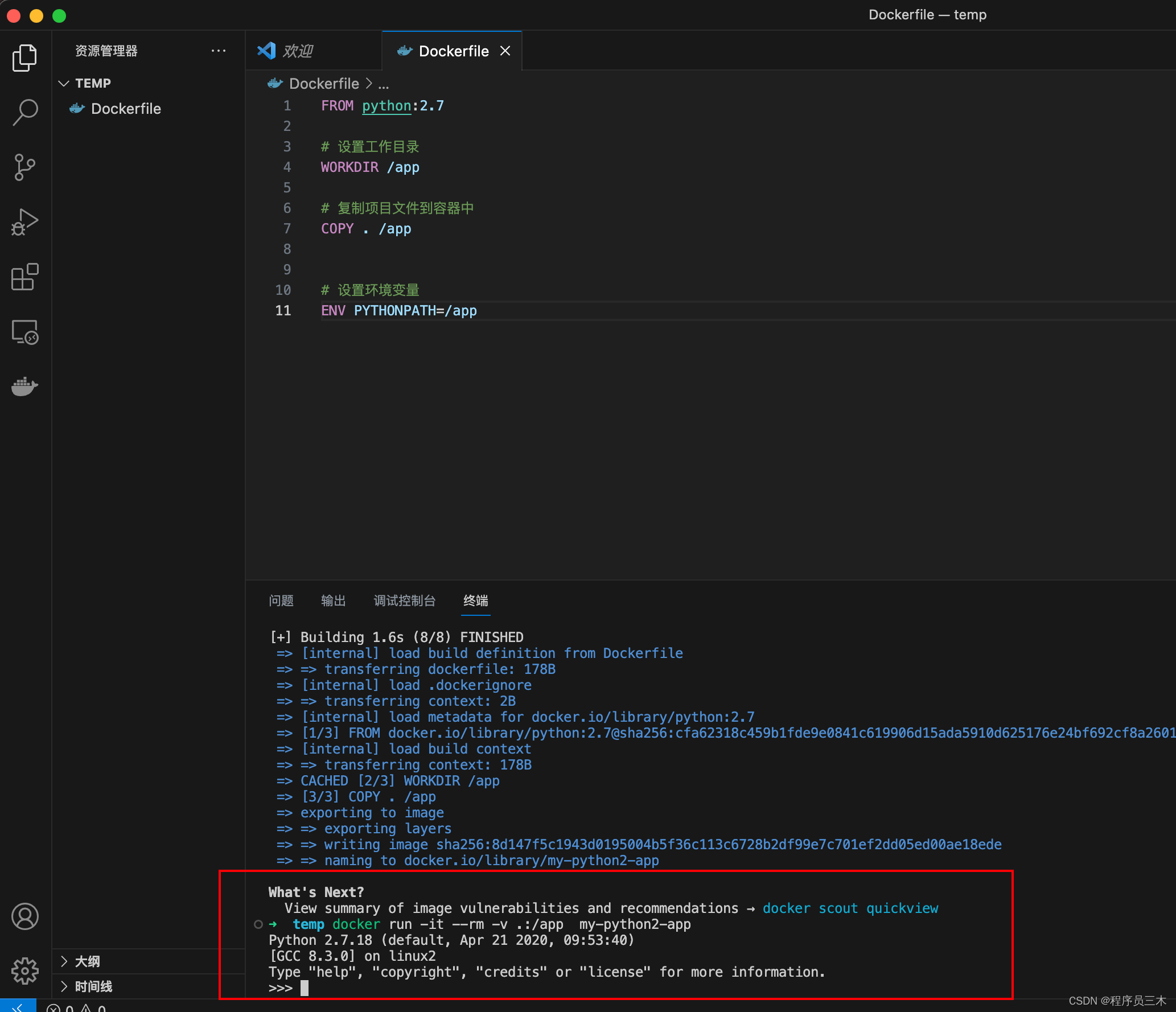
-
安装 VS Code 插件:在 VS Code 中,安装 “Dev Containers” 扩展。这个扩展允许我们连接到 Docker 容器进行开发。
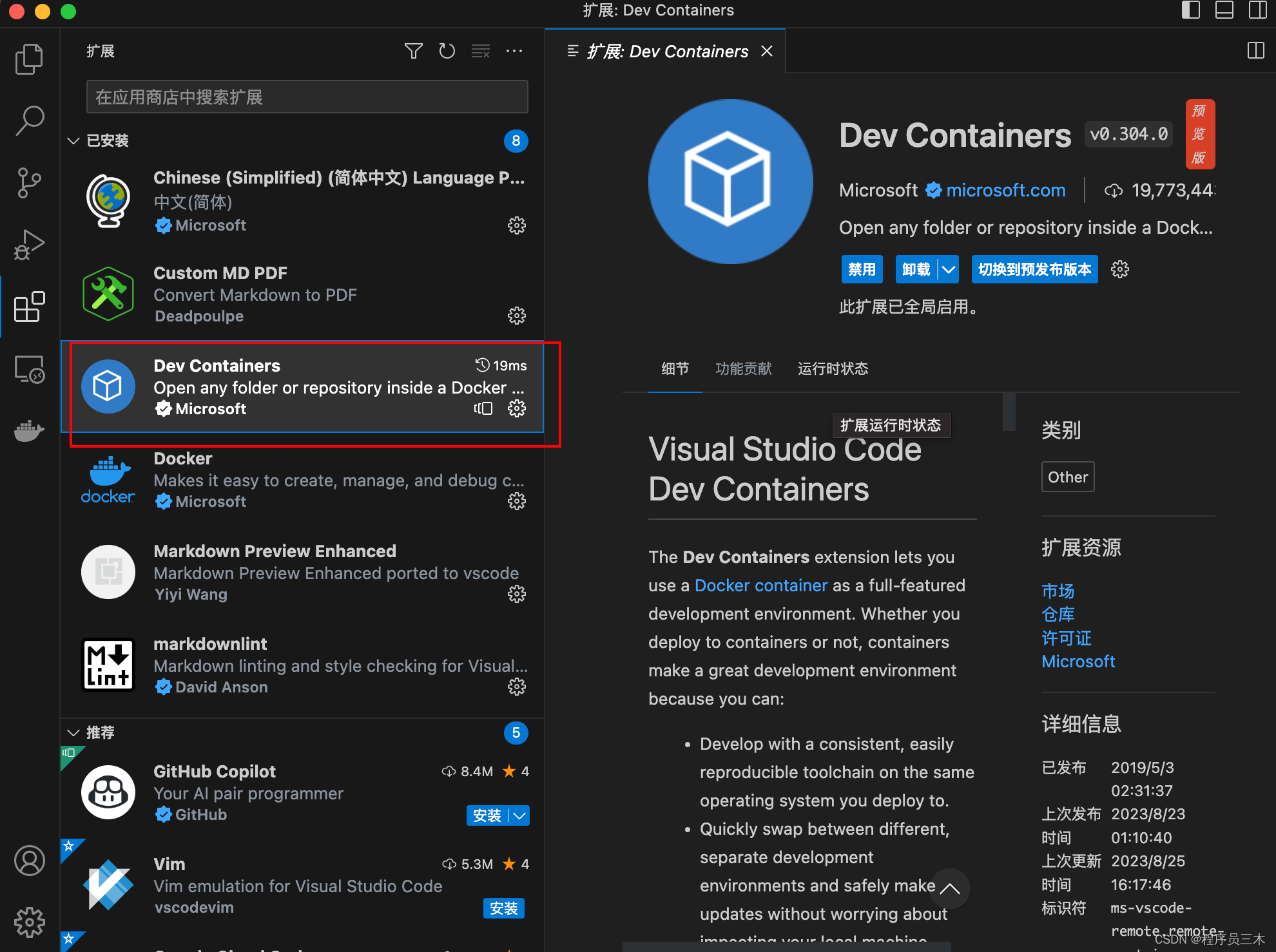
-
连接到容器:在 VS Code 中,点击左边的下图图标,然后选择 “在当前窗口附加”。这将显示一个列表,列出了当前正在运行的容器。
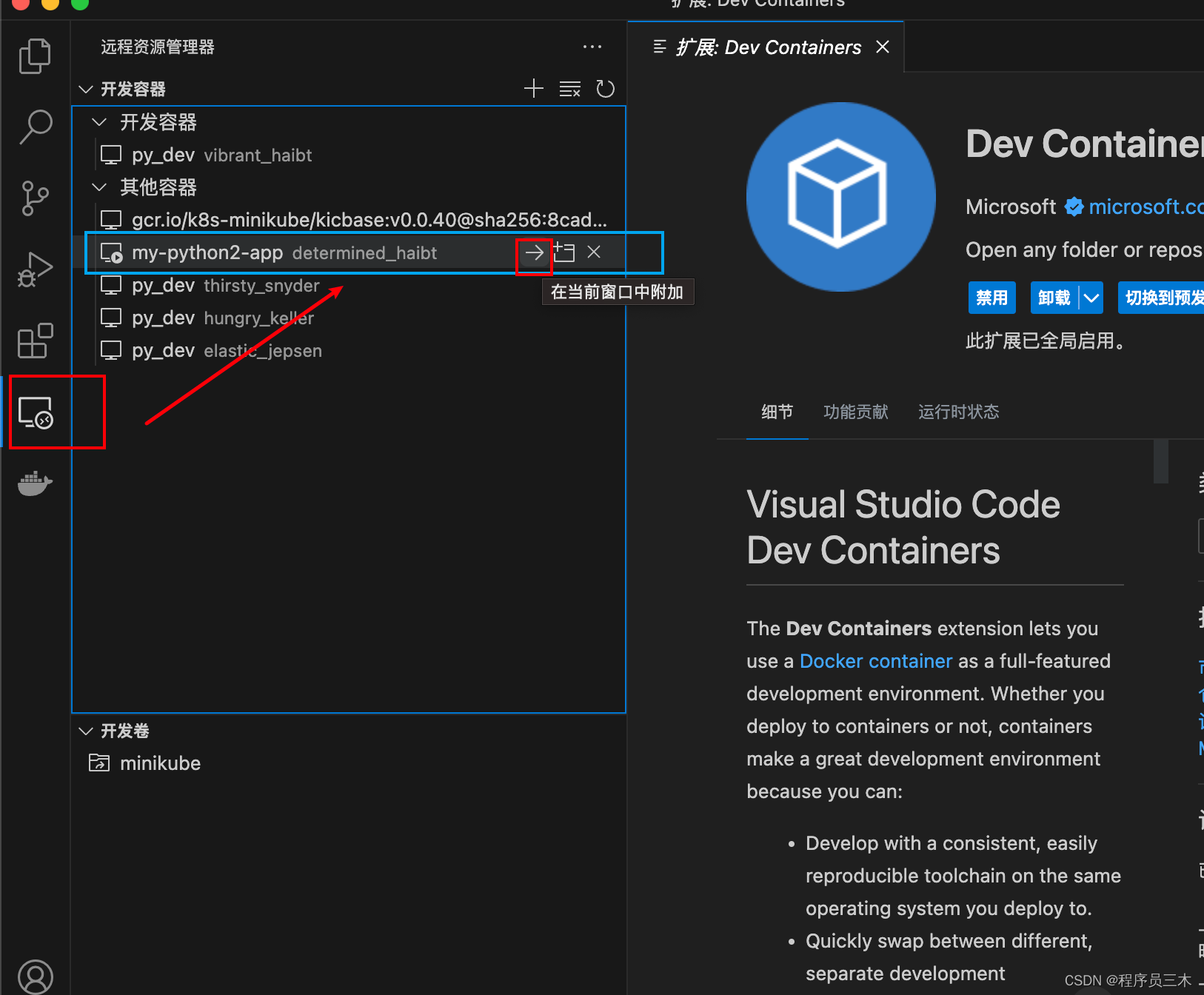
-
选择容器:从列表中选择刚刚运行的容器。VS Code 将尝试连接到选定的容器。
- 连接成功,打开工作目录即可看到咱们的文件。

- 文件打开成功将显示如下
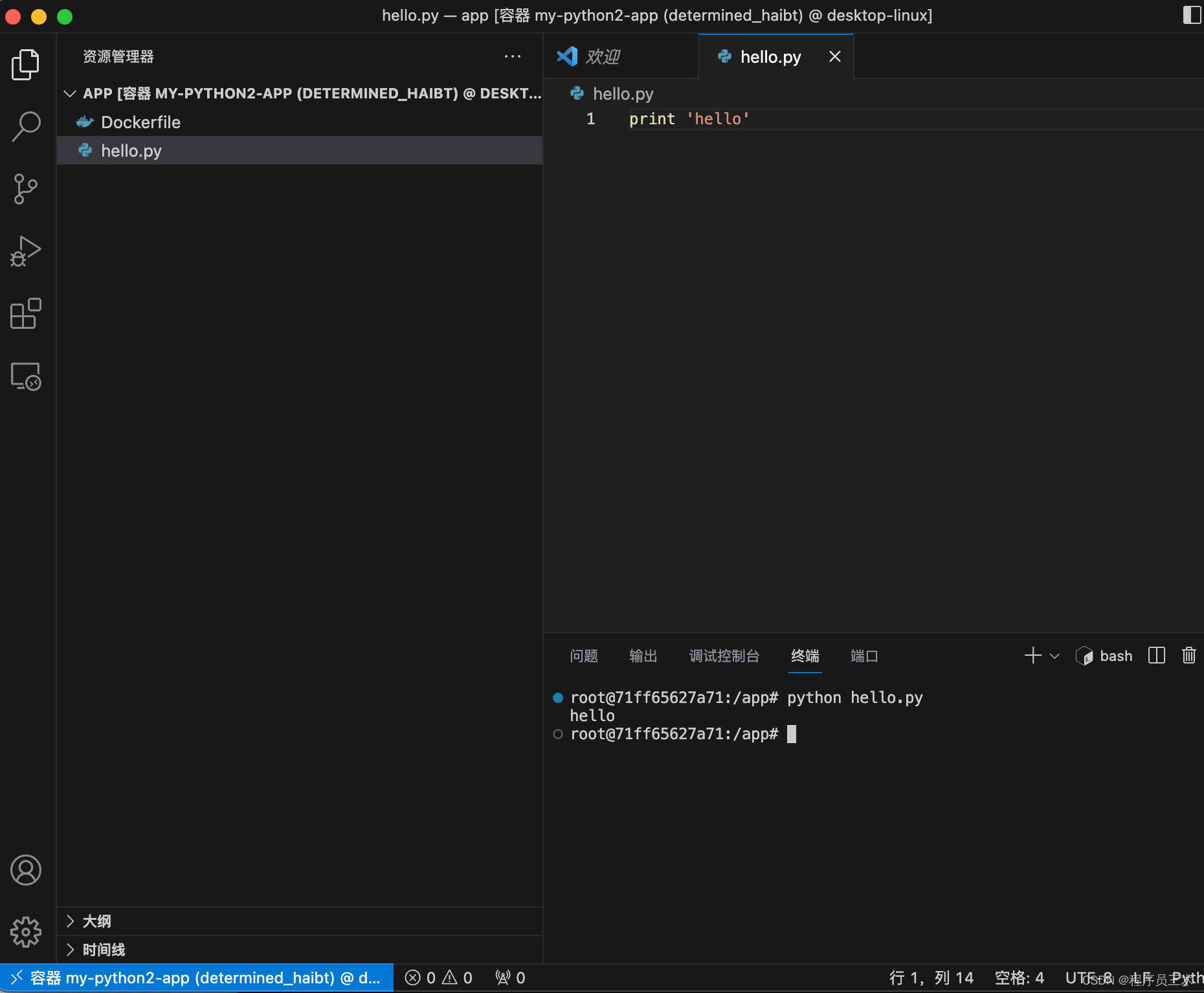
10. 开发,容器里写的代码,由于前面挂在了目录(-v .:/app),所以会在本地持久化,docker 保持无状态。
如果对你有帮助的话,可以给个小小👍+收藏吗
相关文章:

M1 Pro 利用docker 搭建pytho2的开发环境,以vscode连接开发为例
使用 M1 Pro (不支持python2的安装)开发,需要使用 Python 2.7 的环境,在使用 pyenv 安装 Python 2 时遇到了各种奇怪的问题。最终,我决定使用 Docker 搭建开发环境,并使用 VS Code 连接到本地容器。以下是详…...
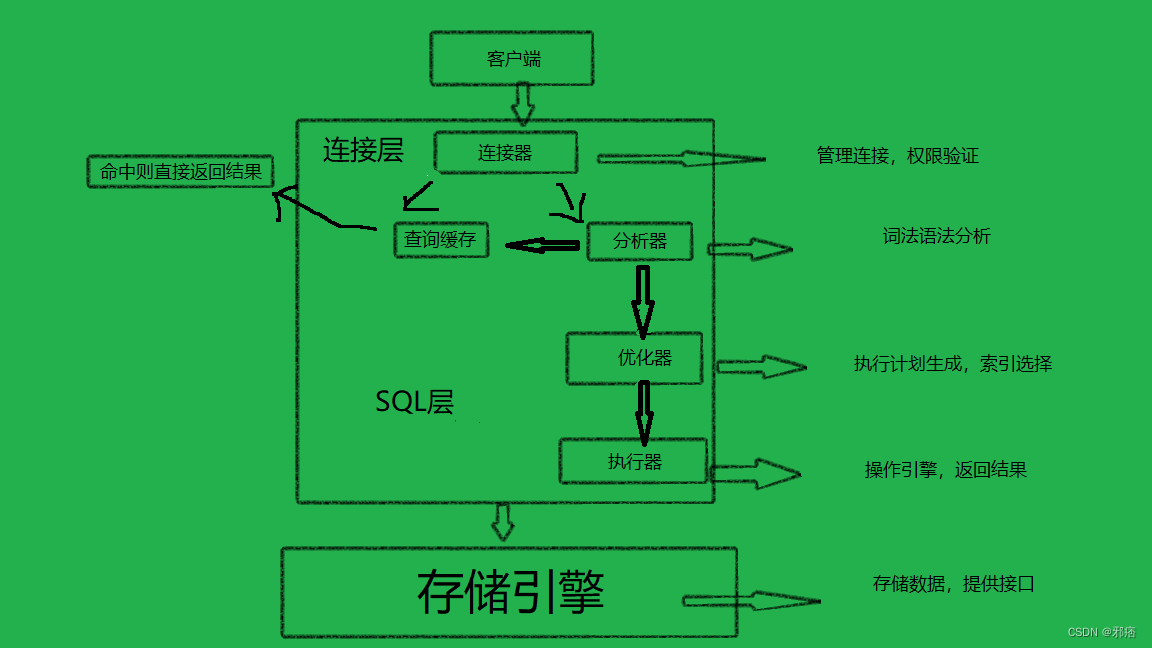
MySQL概述,架构原理
一.MySQL简介 MySQL是一个关系型数据库管理系统,由瑞典的MySQL AB公司开发,后被oracle公司收购,MySQL是当下最流行的关系型数据库管理系统之一,在WEB应用方面,MySQL是最好的RDBMS(Relational Database Man…...
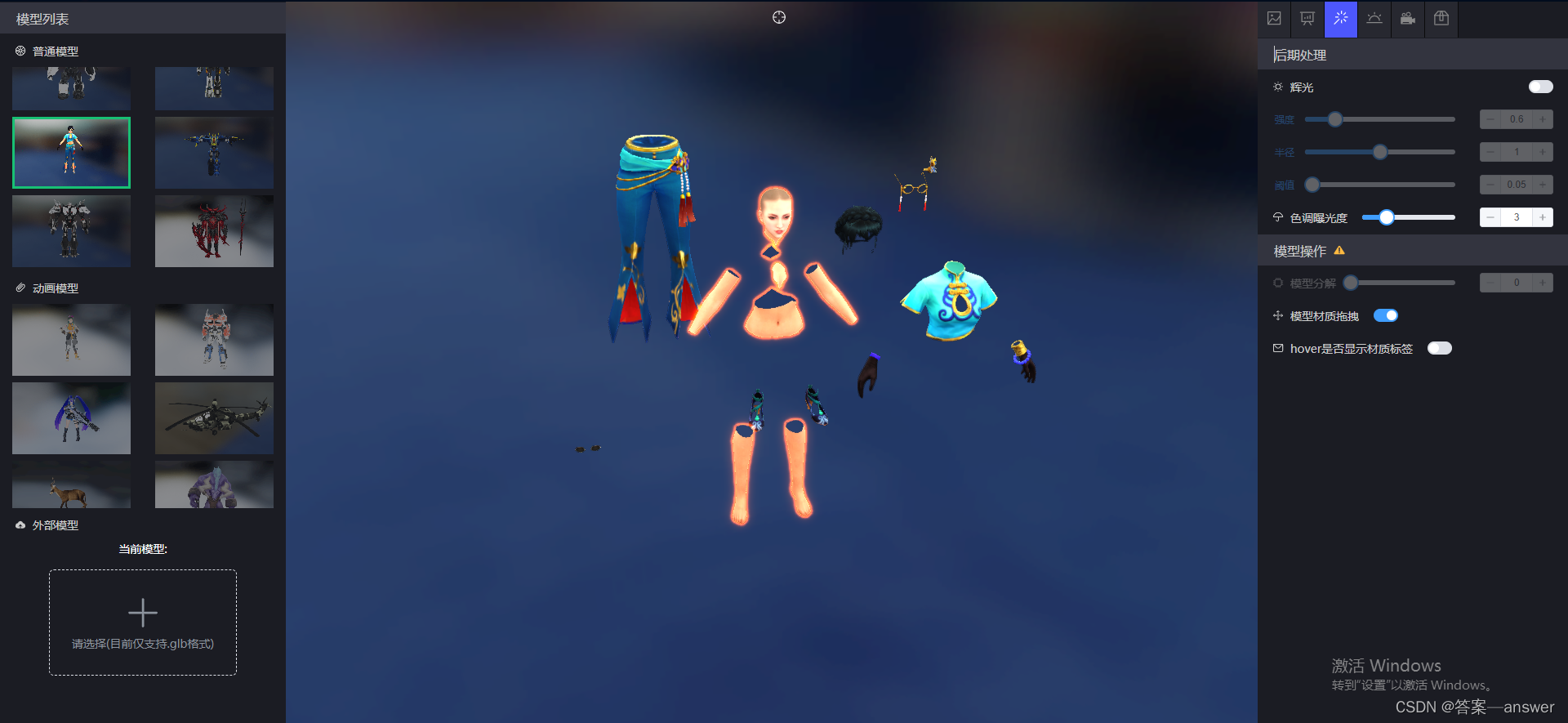
Three.js实现模型,模型材质可拖拽效果 DragControls
Three.js提供了一个拖拽的API DragControls 用于实现模型材质拖拽效果 DragControls:是一个用于在Three.js中实现拖拽控制的辅助类。它简化了在Three.js中实现拖拽物体的过程。 DragControls的构造函数接受三个参数: objects:一个包含需要…...
牛顿法与正则化)
机器学习笔记之优化算法(二十)牛顿法与正则化
机器学习笔记之优化算法——再回首:牛顿法与正则化 引言回顾:经典牛顿法及其弊端牛顿法:算法步骤迭代过程中可能出现的问题正则化 Hessian Matrix \text{Hessian Matrix} Hessian Matrix与相应问题 引言 本节我们介绍经典牛顿法在训练神经网络过程中的迭…...

【Go 基础篇】深入探索:Go语言中的切片遍历与注意事项
嗨,Go语言学习者!在我们的编程旅程中,切片(Slice)是一个极其重要的工具。它可以帮助我们处理各种类型的数据,从而让我们的代码更加灵活和高效。本文将围绕Go语言中切片的遍历方法以及在遍历时需要注意的事项…...

一些经典的SQL语句
查sql中as的用法搜索到的一些经典的sql语句 convert(2008-11-20 18:03:50) In:等值连接,用来查找多表相同字段的记录 Not In:非等值连接,用来查找不存在的记录 Inner join:内连接,主要用来查找都符合条件的记录 Left join:左连接ÿ…...

〔018〕Stable Diffusion 之 批量替换人脸 篇
✨ 目录 🎈 下载插件🎈 插件基础使用🎈 基础使用效果🎈 批量处理图片🎈 多人脸部替换 🎈 下载插件 如果重绘图片的时候,你只想更换人物面部的话,可以参考这篇文章扩展地址ÿ…...

Unity字符串性能问题
前言 分享一些通过书籍和网络学到的知识 每次动态创建一个string,C#都会在堆内存分配一个内存用来分配字符串,因为C#没有对字符串的缓存机制,会导致每次连接、切割、组合的时候都会申请新的内存,并且抛弃原来的内存,等…...

深入浅出SSD:固态存储核心技术、原理与实战(文末赠书)
名字:阿玥的小东东 学习:Python、C/C 主页链接:阿玥的小东东的博客_CSDN博客-python&&c高级知识,过年必备,C/C知识讲解领域博主 目录 内容简介 作者简介 使用Python做一个计算器 本期赠书 近年来国家大力支持半导体行业࿰…...

关于layui+php,三级联动-编辑回显的问题。
注 忍不住吐槽一波。都什么年代了。现在都前后端分离,但是公司老项目非得用tplayui。。 代码如下 layui.use([form], function () {var form layui.form;//php代码渲染页面的时候,将一级分类id和二级分类id带过来,存到页面input框中&#x…...
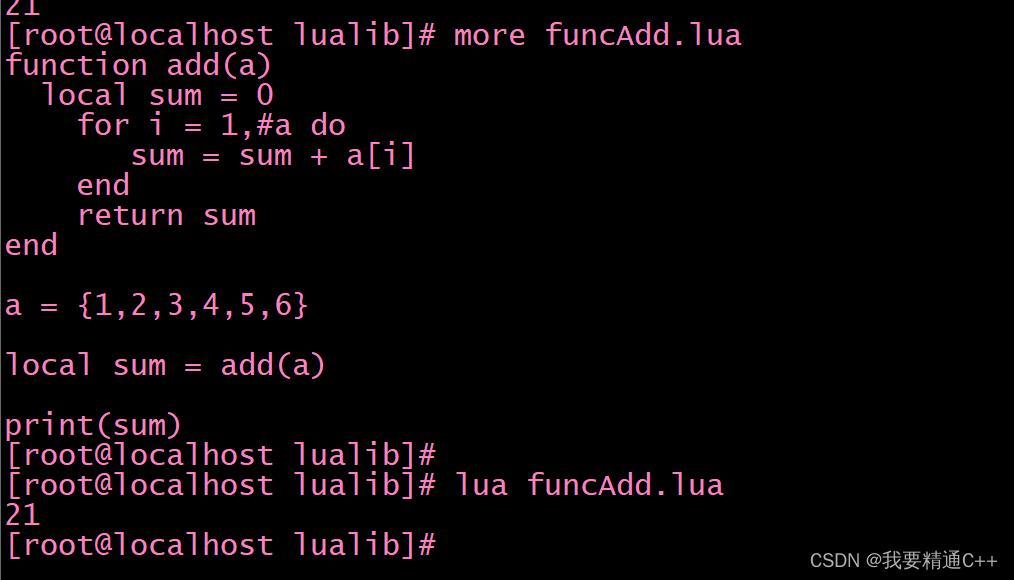
lua的函数
1.一个示例实现列表的元素的求和 [root]# more funcAdd.lua function add(a)local sum 0for i 1,#a dosum sum a[i]endreturn sum enda {1,2,3,4,5,6}local sum add(a)print(sum)...

pytorch/tensorflow 直接给张量中的某个位置的值赋值,操作不可导。
问题:给一个tensor A中[i,j],赋值p。直接操作A[i,j]p可能会导致值覆盖,操作不可导。 解决方案:通过引入一个额外的mask实现。 mask[i,j] 0 mask tf.convert_to_tensor(mask, dtypetf.float32) A (A * mask) (p * (1-mask))p…...

如何使用CSS实现一个平滑滚动到页面顶部的效果(回到顶部按钮)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 平滑滚动到页面顶部的效果(回到顶部按钮)⭐ 创建HTML结构⭐ 编写CSS样式⭐ 编写JavaScript函数⭐ 添加滚动事件监听器⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右…...
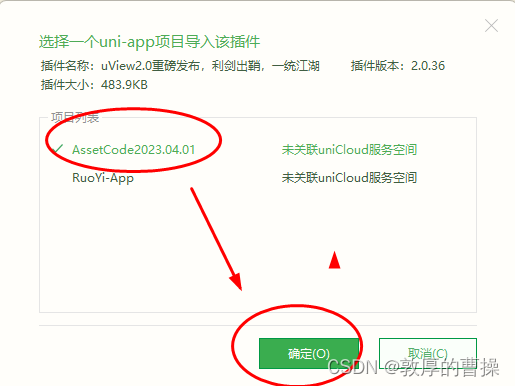
【RuoYi移动端】uniApp导入和引用uView2.0插件
一、打开uiew官网 安装 | uView 2.0 - 全面兼容 nvue 的 uni-app 生态框架 - uni-app UI 框架uView UI,是 uni-app 生态最优秀的 UI 框架,全面的组件和便捷的工具会让您信手拈来,如鱼得水https://uviewui.com/components/install.html 也可直…...

etcd 备份还原
etcd 备份还原 查看 etcdctl 是否已经安装 # quick check if etcdctl is available or not ETCDCTL_API3 etcdctl --help | head安装 etcdctl # 获取 etcd 版本信息 kubectl exec -it etcd-master -n kube-system -- /bin/sh -c ETCDCTL_API3 /usr/local/bin/etcd --version…...

LInux之chrony服务器
目录 场景 重要性 LInux的两个时钟 硬件时钟 系统时钟 NTP协议 Chrony介绍 定义 组成 --- chronyd和chronyc 安装与配置 安装 Chrony配置文件分析 同步时间服务器 chronyc命令 chronyc sources输出分析 其它命令 查看时间服务器的状态 查看时间服务器是否在线 …...

《Flink学习笔记》——第七章 处理函数
为了让代码有更强大的表现力和易用性,Flink 本身提供了多层 API 在更底层,我们可以不定义任何具体的算子(比如 map,filter,或者 window),而只是提炼出一个统一的“处理”(process&a…...
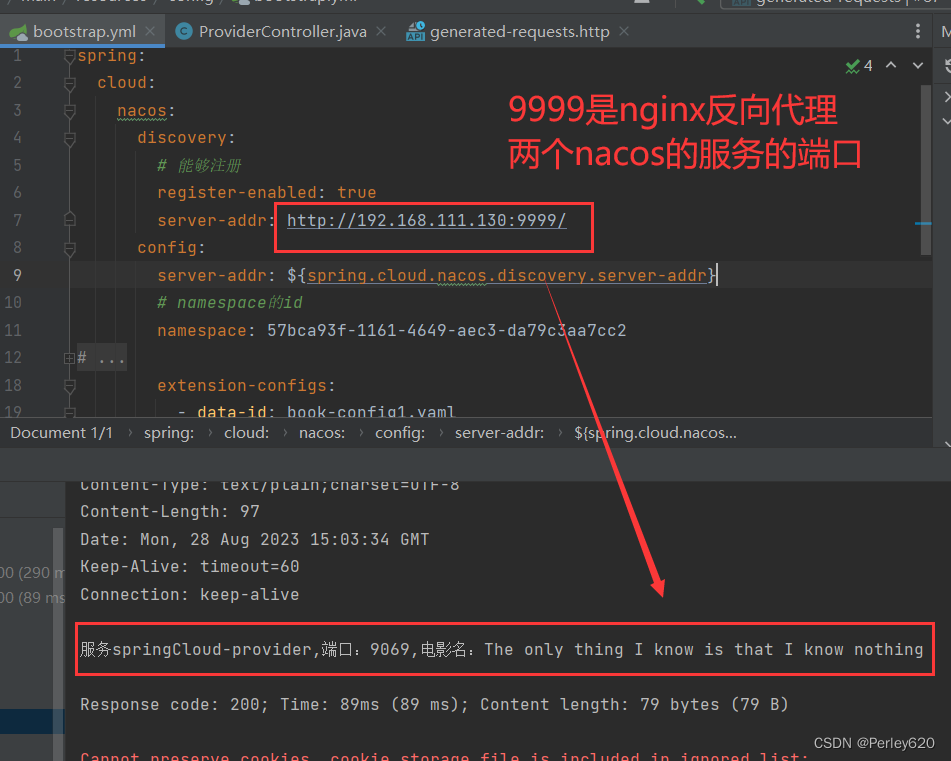
Nacos基础(3)——nacos+nginx 集群的配置和启动 端口开放 nginx反向代理nacos集群
目录 引出nacos集群nginx反向代理nacos集群停止单例nacos准备8848和8858修改cluster.conf配置【配置】修改启动配置文件【配置】开放8858的端口分别以集群方式启动【启动】前端访问查看生产者测试8858nacos nginx反向代理配置代理tcp代理http启动nginx反向代理容器生产者访问测…...

传承精神 缅怀伟人——湖南多链优品科技有限公司赴韶山开展红色主题活动
8月27日上午, 湖南多链优品科技有限公司全体员工怀着崇敬之情,以红色文化为引领,参加了毛泽东同志诞辰130周年的纪念活动。以董事长程小明为核心的公司班子成员以及全国优秀代表近70人一行专赴韶山,缅怀伟人毛泽东同志的丰功伟绩。…...

安全知识普及-如何创建一个安全的密码
文章目录 安全密码的特点创建安全密码的方法为何要创建一个安全的密码推荐阅读 安全密码是一种强化的密码,旨在提供更高级别的安全性,以防止未经授权的访问、数据泄露和其他安全威胁。 安全密码的特点 安全密码,有七大特点,特点如…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
