【LeetCode-面试经典150题-day15】
目录
104.二叉树的最大深度
100.相同的树
226.翻转二叉树
101.对称二叉树
105.从前序与中序遍历序列构造二叉树
106.从中序与后序遍历序列构造二叉树
117.填充每个节点的下一个右侧节点指针Ⅱ
104.二叉树的最大深度
题意:
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
【输入样例】
root=[3,9,20,null,null,15,7]
【输出样例】
3
解题思路:递归
class Solution {public int maxDepth(TreeNode root) {if(root == null){return 0;}//1是当树的根节点不为空时,加上根return 1 + Math.max(maxDepth(root.right),maxDepth(root.left));}
}时间: 击败了100.00%
内存: 击败了36.81%
100.相同的树
题意:
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
【输入样例】
p=[1,2,3], q=[1,2,3]
【输出样例】
true
解题思路:递归
1.先判断当前根节点的值是否一样
2.再判断是否都拥有左子树和右子树
3.递归判断左子树,右子树
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null){return true;}//如果说两者都会null,会在上面的分支语句返回true//这里判断的是只有一方为null的情况下if(p == null || q == null){return false;}//根都不为null,判断值是否相同if(p.val != q.val){return false;}return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}
}时间: 击败了100.00%
内存: 击败了41.80%
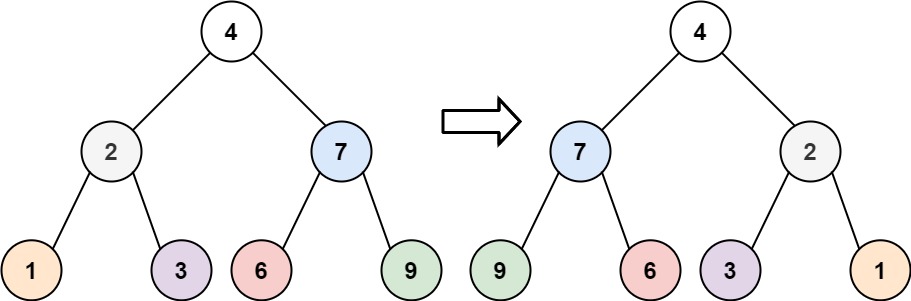
226.翻转二叉树
题意:
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。
【输入样例】
root = [4,2,7,1,3,6,9]
【输出样例】
[4,7,2,9,6,3,1]
解题思路:递归
1. 不断将当前节点的左右子树交换,递归实现
class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return root;}//左右子树交换TreeNode temp = root.right;root.right = root.left;root.left = temp;//交换左子树invertTree(root.left);//交换右子树invertTree(root.right);return root;}
}时间: 击败了100.00%
内存: 击败了88.10%
101.对称二叉树
题意:
给你一个二叉树的根节点
root, 检查它是否轴对称。
【输入样例】
root = [1,2,2,3,4,4,3]
【输出样例】
true
解题思路:递归
1. 递归函数判断节点的左子树和右子树是否对称;把左子树和右子树拆开,题目就转变成了判断相同的树了。
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null){return true;}return cmp(root.left, root.right);}public boolean cmp(TreeNode root1, TreeNode root2){if(root1 == null && root2 == null){return true;}if(root1 == null || root2 == null || root1.val != root2.val){return false;}return cmp(root1.left,root2.right) && cmp(root1.right,root2.left);}
}时间: 击败了100.00%
内存: 击败了82.85%
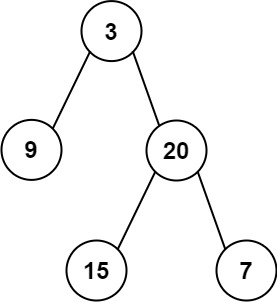
105.从前序与中序遍历序列构造二叉树
题意:
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。
【输入样例】
preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
【输出样例】
[3,9,20,null,null,15,7]
解题思路:
1. 先序遍历的过程是:根 左 右;中序遍历的过程是:左 根 右。
2. 根据规律,首先需要找到的是根节点,inorder数组中根左边的是左子树,根右边的是右子树;
3. 之后分别构造左子树和右子树;
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {private Map<Integer,Integer> indexMap;public TreeNode buildTree(int[] preorder, int[] inorder) {int n = preorder.length;//一共n个节点//构造哈希映射,快速定位根节点indexMap = new HashMap<Integer,Integer>();for(int i=0;i<n;i++){indexMap.put(inorder[i],i);}return myBuildTree(preorder,inorder,0,n-1,0,n-1);}public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {if (preorder_left > preorder_right) {return null;}//前序遍历找到根节点int preorder_root = preorder_left;//中序遍历定位根节点int inorder_root = indexMap.get( preorder[preorder_root]);//建立根节点TreeNode root = new TreeNode(preorder[preorder_root]);//确定左子树节点数目int size_left_subtree = inorder_root - inorder_left;//递归构造左子树,连接到根节点root.left = myBuildTree(preorder,inorder,preorder_left+1,preorder_left+size_left_subtree,inorder_left, inorder_root-1);//递归构造右子树root.right = myBuildTree(preorder,inorder,preorder_left+size_left_subtree+1, preorder_right,inorder_root+1, inorder_right);return root;}
}时间: 击败了99.18%
内存: 击败了23.53%
106.从中序与后序遍历序列构造二叉树
题意:
给定两个整数数组
inorder和postorder,其中inorder是二叉树的中序遍历,postorder是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
【输入样例】
inorder = [9,3,15,20,7],postorder = [9,15,7,20,3]
【输出样例】
[3,9,20,null,null,15,7]
解题思路:
1. 中序遍历的过程是:左 根 右; 后序遍历的过程是:左 右 根 ;。
2. 根据规律,首先需要找到的是根节点,inorder数组中根左边的是左子树,根右边的是右子树;
3. 之后分别构造左子树和右子树;
class Solution {private Map<Integer,Integer> indexMap;public TreeNode buildTree(int[] inorder, int[] postorder) {int n = postorder.length;//一共n个节点//构造哈希映射,快速定位根节点indexMap = new HashMap<Integer,Integer>();for(int i=0;i<n;i++){indexMap.put(inorder[i],i);}return myBuildTree(inorder,postorder,0,n-1,0,n-1);}public TreeNode myBuildTree(int[] inorder,int[] postorder, int inorder_left, int inorder_right,int postorder_left, int postorder_right) {if (postorder_left > postorder_right || inorder_left > inorder_right) {return null;}//后序遍历找到根节点int postorder_root = postorder[postorder_right];//中序遍历定位根节点int inorder_root = indexMap.get(postorder_root);//建立根节点TreeNode root = new TreeNode(postorder_root);//确定左子树节点数目int size_left_subtree = inorder_root - inorder_left;//递归构造左子树,连接到根节点root.left = myBuildTree(inorder, postorder, inorder_left, inorder_root-1,postorder_left,postorder_left+size_left_subtree-1);//递归构造右子树root.right = myBuildTree(inorder,postorder, inorder_root+1, inorder_right,postorder_left+size_left_subtree,postorder_right-1);return root;}
}时间: 击败了99.21%
内存: 击败了61.89%
117.填充每个节点的下一个右侧节点指针Ⅱ
题意:
给定一个二叉树:
struct Node {int val;Node *left;Node *right;Node *next; }填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为
NULL。初始状态下,所有 next 指针都被设置为
NULL。
【输入样例】
root=[1,2,3,4,5,null,7]
【输出样例】
[1,#,2,3,#,4,5,7,#]
解题思路:
利用宽度优先搜索完成本题
/*
// Definition for a Node.
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
*/class Solution {public Node connect(Node root) {if(root== null){return root;}//队列存储节点信息Queue<Node> queue = new LinkedList<>();queue.add(root);while(!queue.isEmpty()){//每一层的数量int levelCount = queue.size();//前一个节点Node pre = null;for(int i=0;i<levelCount;++i){//出队Node node = queue.poll();if(pre != null){//不是第一个节点pre.next = node;}pre = node;//查看左右节点是否为空,不空入队if(node.left != null){queue.add(node.left);}if(node.right != null){queue.add(node.right);}}}return root;}
}时间: 击败了76.40%
内存: 击败了5.16%
相关文章:

【LeetCode-面试经典150题-day15】
目录 104.二叉树的最大深度 100.相同的树 226.翻转二叉树 101.对称二叉树 105.从前序与中序遍历序列构造二叉树 106.从中序与后序遍历序列构造二叉树 117.填充每个节点的下一个右侧节点指针Ⅱ 104.二叉树的最大深度 题意: 给定一个二叉树 root ,返回其…...

git查看和修改项目远程仓库地址
git查看和修改项目远程仓库地址 一、背景 项目代码仓库迁移,需要本地更新远程仓库地址,进行代码同步与提交。 二、查看项目的远程仓库地址 # 查看远程地址 git remote -v # 查看远程仓库信息(分支、地址等) git remote show origin三、修…...
JavaWeb 速通JSON
目录 一、JSON快速入门 1.基本介绍 : 2.定义格式 : 3.入门案例 : 二、JSON对象和字符串的相互转换 1.常用方法 : 2.应用实例 : 3.使用细节 : 三、JSON在Java中的使用 1.基本说明 : 2.应用场景 : 2.1 JSON <---> JavaBean 2.2 JSON <---> List 2.3 JSON …...
20 MySQL(下)
文章目录 视图视图是什么定义视图查看视图删除视图视图的作用 事务事务的使用 索引查询索引创建索引删除索引聚集索引和非聚集索引影响 账户管理(了解非DBA)授予权限 与 账户的相关操作 MySQL的主从配置 视图 视图是什么 通俗的讲,视图就是…...
测试圈的网红工具:Jmeter到底难在哪里?!
雨果的公司最近推出了一款在线购物应用,吸引了大量用户。然而随着用户数量的增加,应用的性能开始出现问题。用户抱怨说购物过程中页面加载缓慢,甚至有时候无法完成订单,小欧作为负责人员迫切需要找到解决方案。 在学习JMeter之前…...
深度学习10:Attention 机制
目录 Attention 的本质是什么 Attention 的3大优点 Attention 的原理 Attention 的 N 种类型 Attention 的本质是什么 Attention(注意力)机制如果浅层的理解,跟他的名字非常匹配。他的核心逻辑就是「从关注全部到关注重点」。 Attention…...
)
简单着色器编写(中下)
这篇我们来介绍另一部分函数。 static unsigned int CreateShader(const std::string& vertexShader, const std::string& fragmentShader) {unsigned int program glCreateProgram();unsigned int vs CompileShader(GL_VERTEX_SHADER,vertexShader);unsigned int f…...
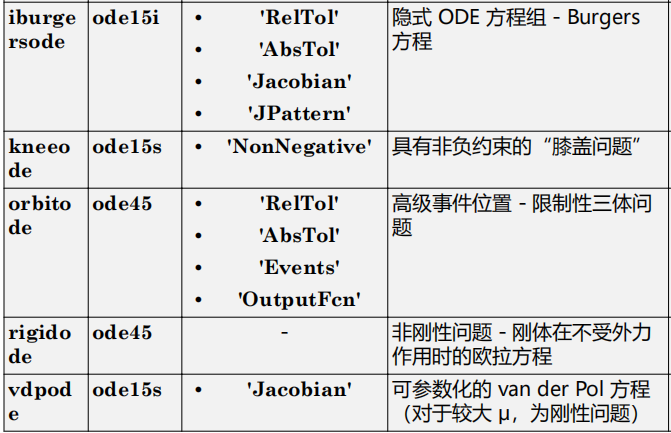
matlab使用教程(24)—常微分方程(ODE)求解器
1.常微分方程 常微分方程 (ODE) 包含与一个自变量 t(通常称为时间)相关的因变量 y 的一个或多个导数。此处用于表示 y 关于 t 的导数的表示法对于一阶导数为 y ′ ,对于二阶导数为 y ′′,依此类推。ODE 的阶数等于 y 在方程中…...

企业级数据共享规模化模式
数据共享正在成为企业数据战略的重要元素。对于公司而言,Amazon Data Exchange 这样的亚马逊云科技服务提供了与其他公司共享增值数据或从这些数据获利的途径。一些企业希望有一个数据共享平台,他们可以在该平台上建立协作和战略方法,在封闭、…...
Web服务器-Tomcat详细原理与实现
Tomcat 安装与使用 :MAC 安装配置使用Tomcat - 掘金 安装后本计算机就相当于一台服务器了!!! 方式一:使用本地安装的Tomcat 1、将项目文件移动到Tomcat的webapps目录下。 2、启动Tomcat 3、在浏览器输入想要加载的…...
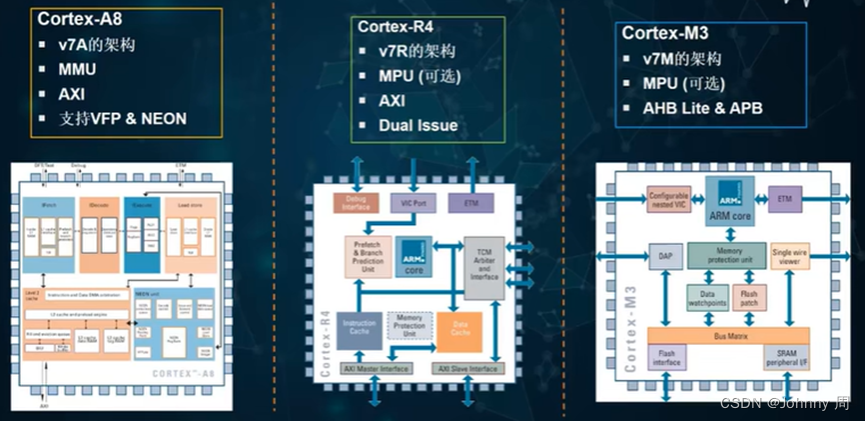
ARM处理器核心概述
一、基于ARM处理器的嵌入式系统 ARM核深度嵌入SOC中,通过JTAG口进行外部调试。计通常既有外部内存又有内部内存,从而支持不通的内存宽度、速度和大小。一般会包含一个中断控制器。可能包含一些Primece外设,需要从ARM公司取得授权。总线使用A…...
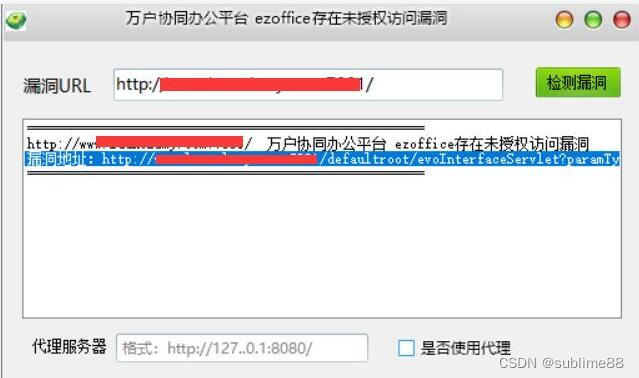
万户协同办公平台 ezoffice存在未授权访问漏洞 附POC
文章目录 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC1. 万户协同办公平台 ezoffice简介2.漏洞描述3.影响版本4.fofa查询语句5.漏洞复现6.POC&EXP7.整改意见8.往期回顾 万户协同办公平台 ezoffice存在未授权访问漏洞 附POC 免责声明:请勿利用文章内的相…...
使用ctcloss训练矩阵生成目标字符串
首先我们需要明确 c t c l o s s ctcloss ctcloss是用来做什么的。比如说要生成的目标字符串长度为 l l l,而这个字符串包含 s s s个字符,字符串允许的最大长度为 L L L,这里认为一个位置是一个时间步,就是一拍,记为 T…...
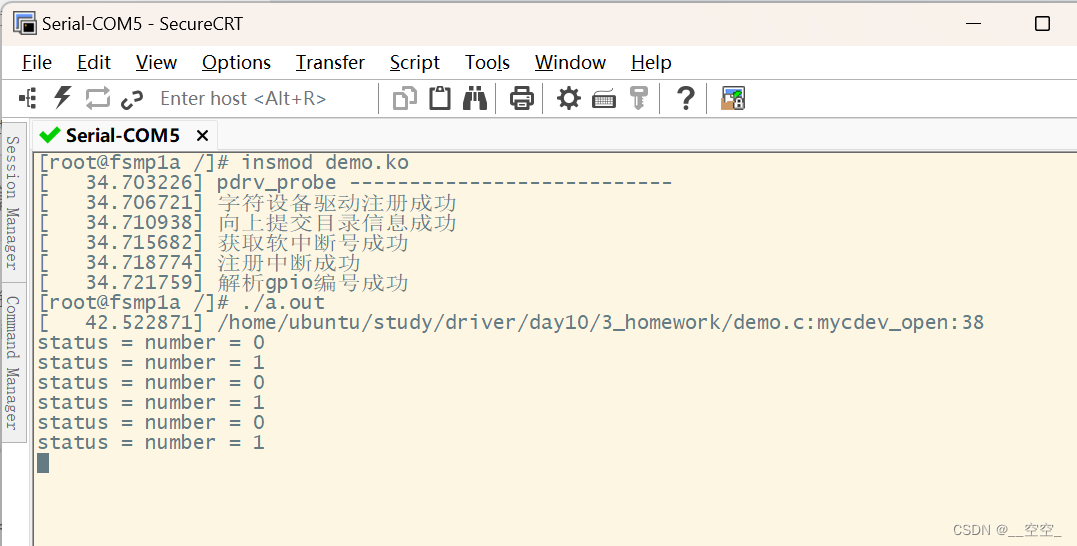
驱动 - 20230829
练习 基于platform实现 在根节点下,增加设备树 myplatform {compatible"hqyj,myplatform";interrupts-extended<&gpiof 9 0>, <&gpiof 7 0>, <&gpiof 8 0>;led1-gpio<&gpioe 10 0>;reg<0x12345678 59>;}…...

数组(个人学习笔记黑马学习)
一维数组 1、定义方式 #include <iostream> using namespace std;int main() {//三种定义方式//1.int arr[5];arr[0] 10;arr[1] 20;arr[2] 30;arr[3] 40;arr[4] 50;//访问数据元素/*cout << arr[0] << endl;cout << arr[1] << endl;cout &l…...

layui表格事件分析实例
在 layui 的表格组件中,区分表头事件和行内事件是通过事件类型(toolbar 和 tool)以及 lay-filter 值来实现的。 我们有一个表格,其中有一个工具栏按钮和操作按钮。我们将使用 layui 的 table 组件来处理这些事件。 HTML 结构&…...

Android NDK JNI与Java的相互调用
一、Jni调用Java代码 jni可以调用java中的方法和java中的成员变量,因此JNIEnv定义了一系列的方法来帮助我们调用java的方法和成员变量。 以上就是jni调用java类的大部分方法,如果是静态的成员变量和静态方法,可以使用***GetStaticMethodID、CallStaticObjectMethod等***。就…...

装备制造企业如何执行精益管理?
导 读 ( 文/ 2358 ) 精益管理是一种以提高效率、降低成本和优化流程为目标的管理方法。装备制造行业具备人工参与度高,产成品价值高,质量要求高的特点。 在装备制造企业中实施精益管理可以帮助企业提高竞争力、提升生产效率并提供高质量的产品。本文将…...

PHP8中自定义函数-PHP8知识详解
1、什么是函数? 函数,在英文中的单词是function,这个词语有功能的意思,也就是说,使用函数就是在编程的过程中,实现一定的功能。即函数就是实现一定功能的一段特定代码。 在前面的教学中,我们已…...

虚拟化技术:云计算发展的核心驱动力
文章目录 虚拟化技术的概念和作用虚拟化技术的优势虚拟化技术对未来发展的影响结论 🎉欢迎来到AIGC人工智能专栏~虚拟化技术:云计算发展的核心驱动力 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客🎈该系…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...