C++--完全背包问题
1.【模板】完全背包_牛客题霸_牛客网
你有一个背包,最多能容纳的体积是V。
现在有n种物品,每种物品有任意多个,第i种物品的体积为vivi ,价值为wiwi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
输入描述:
第一行两个整数n和V,表示物品个数和背包体积。
接下来n行,每行两个数vivi和wiwi,表示第i种物品的体积和价值。
1≤n,V≤10001≤n,V≤1000
输出描述:
输出有两行,第一行输出第一问的答案,第二行输出第二问的答案,如果无解请输出0。
示例1
输入:
2 6 5 10 3 1输出:10 2示例2
输入:
3 8 3 10 9 1 10 1输出:20 0说明:
无法恰好装满背包。示例3
输入:
6 13 13 189 17 360 19 870 14 184 6 298 16 242输出:596 189说明:
可以装5号物品2个,达到最大价值298*2=596,若要求恰好装满,只能装1个1号物品,价值为189.
#include <iostream>
#include <string.h>
using namespace std;
int main()
{int n, V;cin >> n >> V;int v[n];int w[n];for (int i = 0; i < n; i++) cin >> v[i] >> w[i];int dp[n + 1][V + 1];//初始化memset(dp, 0, sizeof dp);for (int i = 1; i <= n; i++){for (int j = 0; j <= V; j++){//动态转移方程dp[i][j] = dp[i - 1][j];if (j - v[i - 1] >= 0) dp[i][j] = max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);}}cout << dp[n][V] << endl;memset(dp, 0, sizeof dp);for (int i = 1; i <= V; i++) dp[0][i] = -1;for (int i = 1; i <= n; i++){for (int j = 0; j <= V; j++){dp[i][j] = dp[i - 1][j];if (j - v[i - 1] >= 0 && dp[i][j - v[i - 1]] != -1) dp[i][j] = max(dp[i][j], dp[i][j - v[i - 1]] + w[i - 1]);}}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}2.零钱兑换 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1示例 2:
输入:coins =[2], amount =3输出:-1示例 3:
输入:coins = [1], amount = 0 输出:0
class Solution {
public:int coinChange(vector<int>& coins, int amount) {int n=coins.size();vector<int> dp(amount+1);//创建dp表for(int i=1;i<=amount;i++) dp[i]=0x3f3f3f3f;//初始化,寻找最小值for(int i=1;i<=n;i++){for(int j=coins[i-1];j<=amount;j++){if(j-coins[i-1]>=0){dp[j]=min(dp[j],dp[j-coins[i-1]]+1);//动态转移方程}}}return dp[amount]>=0x3f3f3f3f?-1:dp[amount];//返回值}
};3.零钱兑换二 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数数组
coins表示不同面额的硬币,另给一个整数amount表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回
0。假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5] 输出:4 解释:有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1示例 2:
输入:amount = 3, coins = [2] 输出:0 解释:只用面额 2 的硬币不能凑成总金额 3 。示例 3:
输入:amount = 10, coins = [10] 输出:1
class Solution {
public:int change(int amount, vector<int>& coins) {int n=coins.size();vector<int> dp(amount+1);dp[0]=1;//初始化for(int i=1;i<=n;i++){for(int j=coins[i-1];j<=amount;j++){dp[j]+=dp[j-coins[i-1]];//动态转移方程}}return dp[amount];//返回值}
};4.完全平方数 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数
n,返回 和为n的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,
1、4、9和16都是完全平方数,而3和11不是。示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
class Solution {
public:int numSquares(int n) {int m=sqrt(n);vector<int> dp(n+1,0x3f3f3f3f);//初始化dp[0]=0;for(int i=1;i<=m;i++){for(int j=i*i;j<=n;j++){dp[j]=min(dp[j],dp[j-i*i]+1);//动态转移方程}}return dp[n]; }
};相关文章:

C++--完全背包问题
1.【模板】完全背包_牛客题霸_牛客网 你有一个背包,最多能容纳的体积是V。 现在有n种物品,每种物品有任意多个,第i种物品的体积为vivi ,价值为wiwi。 (1)求这个背包至多能装多大价值的物品? ࿰…...

显示本地 IP 地址和相应的 QR 码,方便用户共享和访问网络信息
这段代码使用了 wxPython、socket、qrcode 和 PIL(Python Imaging Library)模块来生成一个具有本地 IP 地址和相应 QR 码的窗口应用程序。 C:\pythoncode\new\showipgenqrcode.py 让我们逐行解释代码的功能: import wx:导入 wx…...

为什么建议同时学多门编程语言
晨读一本名叫《4点起床》的书,书中有一段描述与最近学习编制语言时自己的感受完全一致。算是一个小经验,分享给大家。 书中有一章的标题为《同时学六国语言记起来比较快》,其中有两段描述如下: 为什么我推荐大家同时学不同的语言…...

langchain agent
zero-shot-react-description 代码 from langchain.agents import initialize_agent from langchain.llms import OpenAI from langchain.tools import BaseTool import os os.environ[OPENAI_API_KEY]"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"# 搜索…...
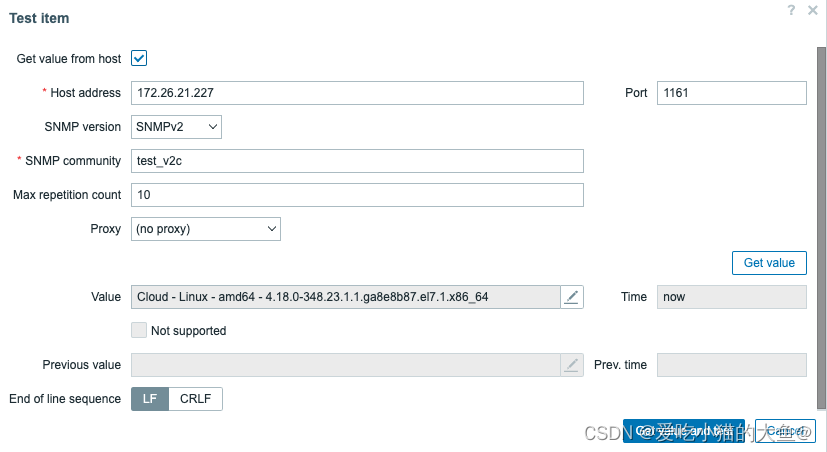
Zabbix下载安装及SNMP Get使用
帮助文档:6. Zabbix Appliance 一、zabbix下载安装 1、获取Zabbix Appliance镜像 Download Zabbix appliance 2、使用该镜像创建虚拟机 3、打开虚拟机控制台自动安装,等待安装完成即可 默认配置 系统/数据库:root:zabbix Zabbix 前端&am…...
freee Programming Contest 2023(AtCoder Beginner Contest 310)
文章目录 A - Order Something Else(模拟)B - Strictly Superior(模拟)C - Reversible(模拟)D - Peaceful Teams(DFS状压)E - NAND repeatedly(普通dp)F - Make 10 Again(状态压缩概率dp&#x…...

恒运资本:概念股是什么意思
概念股是指在特定的经济布景、方针环境、职业远景或社会热点等方面具有某种特别的发展远景和投资价值的股票。在投资者心目中,概念股的危险较大,可是或许带来高于商场平均水平的收益率。那么,概念股到底是什么意思?在本文中&#…...
十九、状态模式
一、什么是状态模式 状态(State)模式的定义:对有状态的对象,把复杂的“判断逻辑”提取到不同的状态对象中,允许状态对象在其内部状态发生改变时改变其行为。 状态模式包含以下主要角色: 环境类(…...
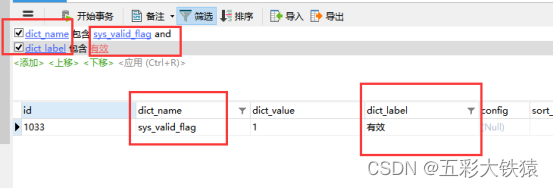
MySQL用navicat工具对表进行筛选查找
这个操作其实很简单,但是对于没操作的人来说,就是不会呀。所以小编出这一个详细图解,希望能够帮助到大家。话不多说看图。 第一步: 点进一张表,点击筛选。 第二步: 点击添加 第三步: 选择要…...

音视频 ffplay简单过滤器
视频旋转 ffplay -i test.mp4 -vf transpose1视频反转 ffplay test.mp4 -vf hflip ffplay test.mp4 -vf vflip视频旋转和反转 ffplay test.mp4 -vf hflip,transpose1音频变速播放 ffplay -i test.mp4 -af atempo2视频变速播放 ffplay -i test.mp4 -vf setptsPTS/2音视频同…...

索引 事务 存储引擎
################索引##################### 一、索引的概念 ●索引是一个排序的列表,在这个列表中存储着索引的值和包含这个值的数据所在行的物理地址(类似于C语言的链表通过指针指向数据记录的内存地址)。 ●使用索引后可以不用扫描全表来…...
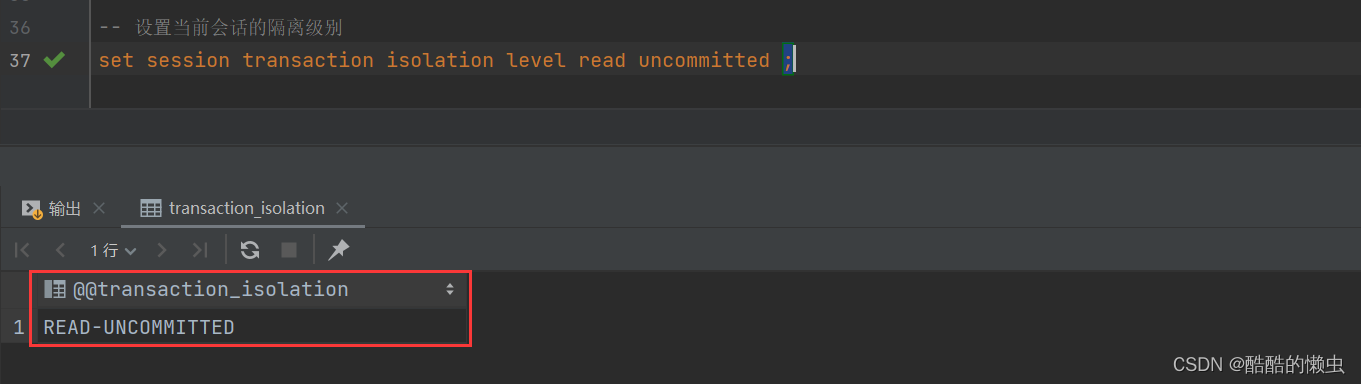
MySQL— 基础语法大全及操作演示!!!(事务)
MySQL—— 基础语法大全及操作演示(事务) 六、事务6.1 事务简介6.2 事务操作6.2.1 未控制事务6.2.2 控制事务一6.2.3 控制事务二 6.3 事务四大特性6.4 并发事务问题6.5 事务隔离级别 MySQL— 基础语法大全及操作演示!!!…...
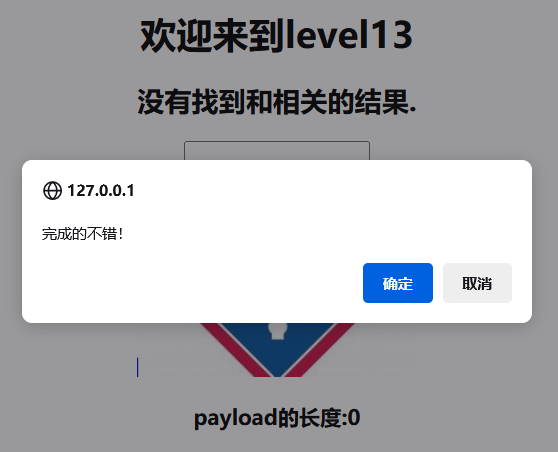
xsschallenge1~13通关详细教程
文章目录 XSS 挑战靶场通关level1level2level3level4level5level6level7level8level9level10level11level12level13 XSS 挑战靶场通关 level1 通过观察发现这个用户信息可以修改 那么我们直接输入攻击代码 <script>alert(/wuhu/)</script>弹框如下: …...

考生作弊行为分析算法
考生作弊行为分析系统利用pythonyolo系列网络模型算法框架,考生作弊行为分析算法利用图像处理和智能算法对考生的行为进行分析和识别,经过算法服务器的复杂计算和逻辑判断,算法将根据考生行为的特征和规律,判定是否存在作弊行为。…...

Python 操作 Redis 数据库介绍
Redis 作为常用的 NoSql 数据库,主要用于缓存数据,提高数据读取效率,那在 Python 中应该如果连接和操作 Redis 呢?今天就为大概简单介绍下,在 Python 中操作 Redis 常用命令。 安装 redis 首先还是需要先安装 redis …...

十年JAVA搬砖路——软件工程概述
软件工程是一门关注软件开发过程的学科,它涉及到软件的设计、开发、测试、部署和维护等方面。软件工程的目标是通过系统化的方法和工具,以确保软件项目能够按时、按预算和按要求完成。 • 软件工程的7个基本概念: 软件生命周期:软…...
前后端项目部署上线详细笔记
部署 参考文章:如何部署网站?来比比谁的方法多 - 哔哩哔哩大家好,我是鱼皮,不知道朋友们有没有试着部署过自己开发的网站呢?其实部署网站非常简单,而且有非常多的花样。这篇文章就给大家分享几种主流的前端…...
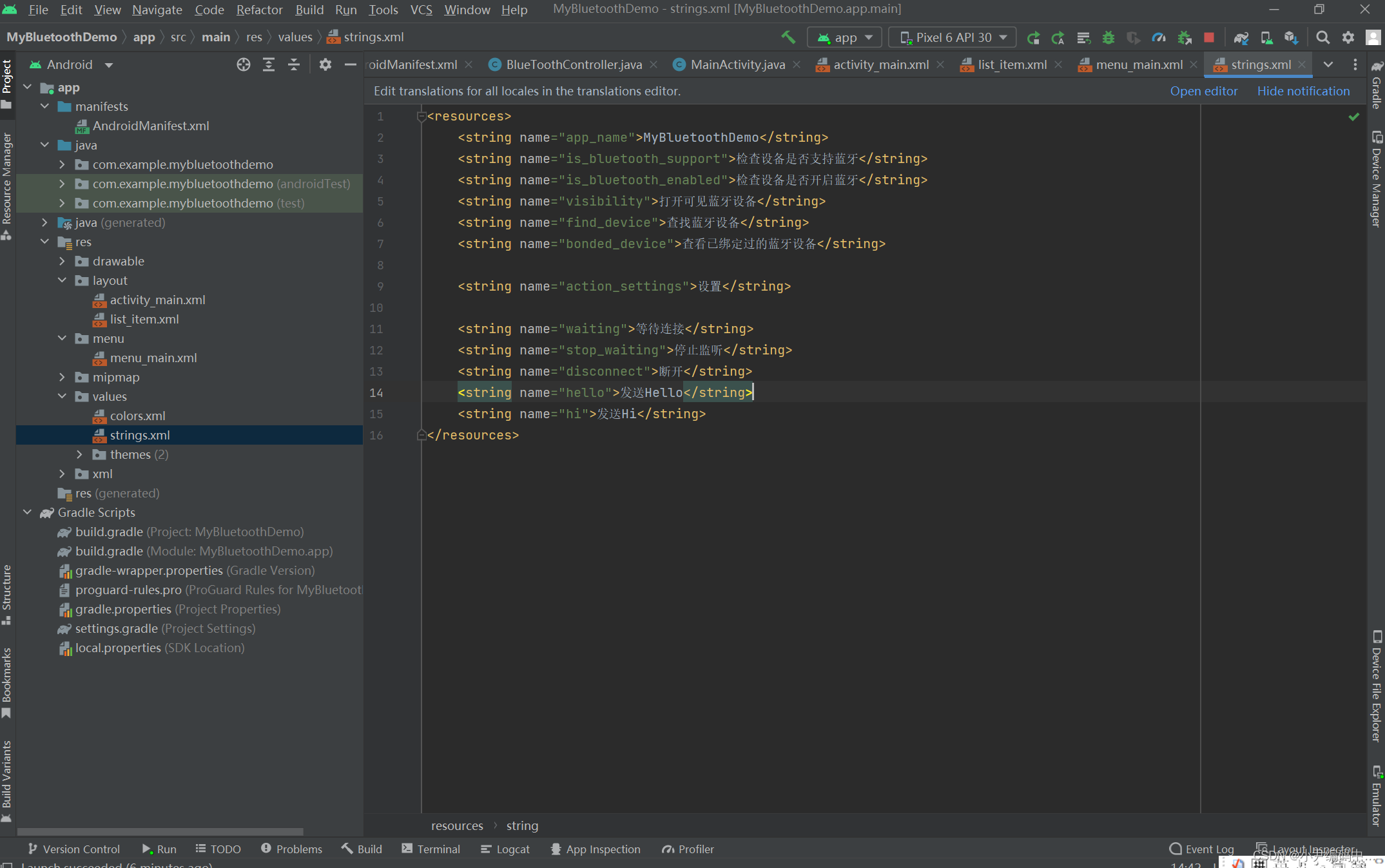
Android 蓝牙开发( 二 )
前言 上一篇文章给大家分享了Android蓝牙的基础知识和基础用法,不过上一篇都是一些零散碎片化的程序,这一篇给大家分享Android蓝牙开发实战项目的初步使用 效果演示 : Android蓝牙搜索,配对,连接,通信 Android蓝牙实…...
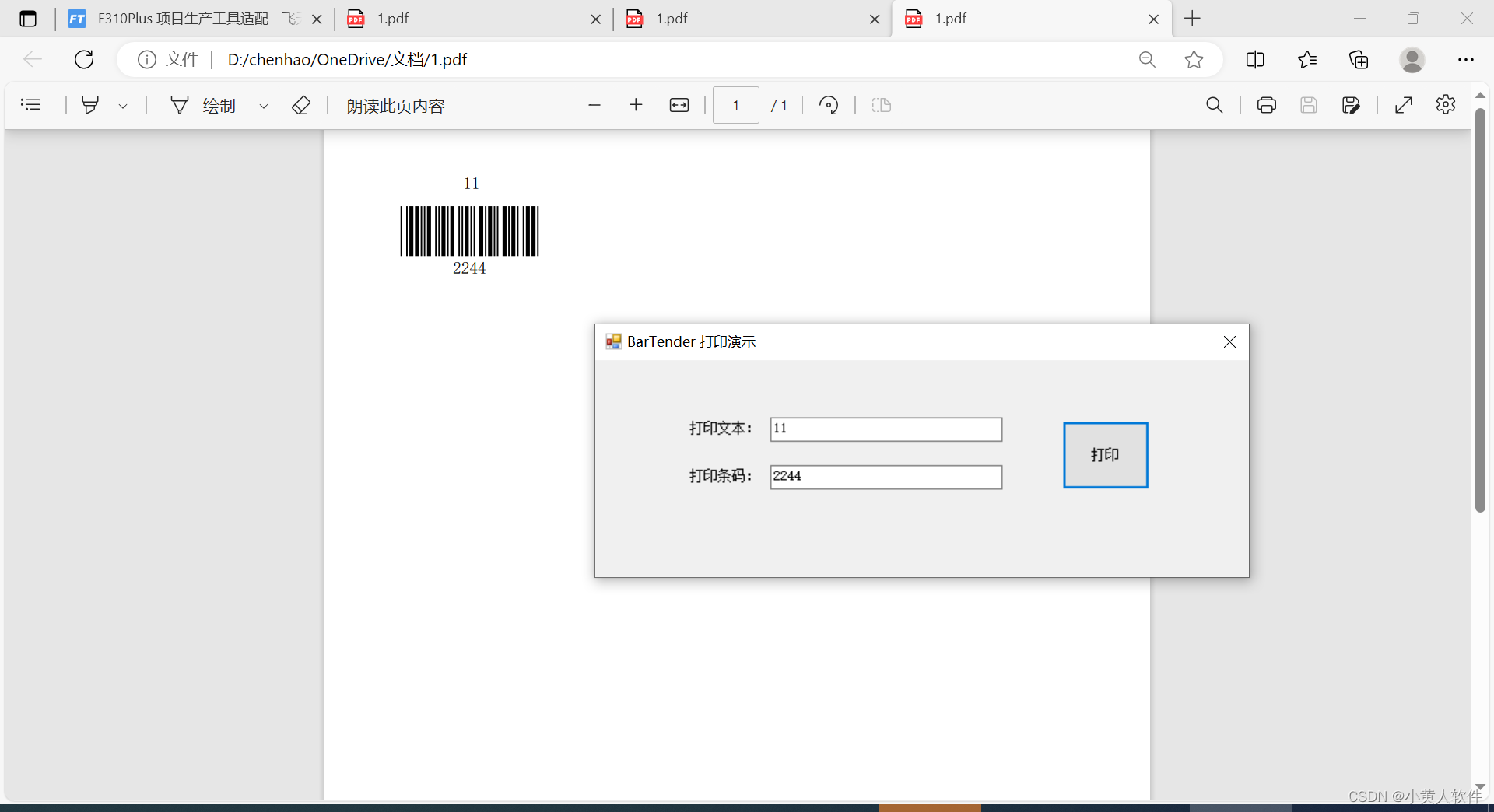
C#调用barTender打印标签示例
使用的电脑需要先安装BarTender 我封装成一个类 using System; using System.Windows.Forms;namespace FT_Tools {public class SysContext{public static BarTender.Application btapp new BarTender.Application();public static BarTender.Format btFormat;public void Q…...
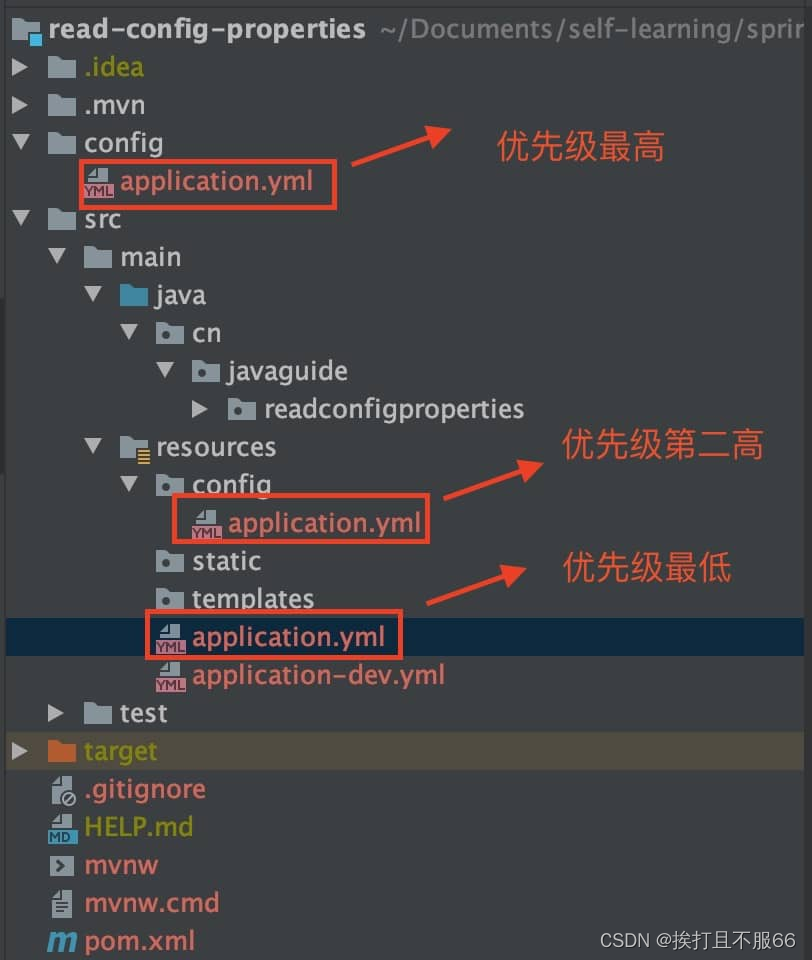
Spring——Spring读取文件
文章目录 1.通过 value 读取比较简单的配置信息2.通过ConfigurationProperties读取并与 bean 绑定3.通过ConfigurationProperties读取并校验4. PropertySource 读取指定 properties 文件5.题外话:Spring加载配置文件的优先级 很多时候我们需要将一些常用的配置信息比如阿里云os…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
