论文笔记: 深度学习速度模型构建的层次迁移学习方法 (未完)
摘要: 分享对论文的理解, 原文见 Jérome Simon, Gabriel Fabien-Ouellet, Erwan Gloaguen, and Ishan Khurjekar, Hierarchical transfer learning for deep learning velocity model building, Geophysics, 2003, R79–R93. 这次的层次迁移应该指从 1D 到 2D 再到 3D.
摘要
深度学习具有使用最少的资源 (这里应该是计算资源, 特别是预测时的计算资源) 处理大量地震资料的潜力.
神经网络直接将数据 (即地震记录) 映射到模型 (如速度模型).
由于数据量太大, 直接做 2D 或 3D 不可行, 因此在一个子问题 (1D) 上训练神经网络.
通过迁移学习, 减少了 2D 训练数据的使用量. 注: 如何从 1D 迁移到 2D 是一个核心问题.
root-mean-square 误差为 ( 198 ± 91 198 \pm 91 198±91) m/s.
再次用到了 RMS 速度模型 (参见 论文笔记: 循环神经网络进行速度模型反演).
引言
DL 不仅用于 FWI, 也用于常规处理的各个步骤.
DL-FWI 暂时还不能成为工业标准, 但它有可能在缩短训练时间后超越物理规律驱动的 FWI (即数值模拟 FWI).
当前的 DL-FWI 只处理尺寸小的速度模型 (如 301*301), 可能有些薄层和盐丘, 但总体不具有实际数据的代表性.
Fabien-Ouellet and Sarkar (2020) 的方法可以处理较大规模数据, 但获得的速度模型横向连续性不好 (不符合物理规律, 这个用我们的边界提取辅助任务可能会缓解).
共中心点 CMP 道集看来用得比较多, 我们用的是共炮点 CSP 道集.
图像处理任务使用几万至几百万带标签实际数据进行训练, 地震数据可能有这么多, 但标签非常少 (如果不是没有的话). 这确实是大家面临的难题.
方法
问题: 从叠前数据直接估计 (反演) 倾斜分层声波速度模型. 注: 声波太简单了吧.
输入: n t × n h × n x n_t \times n_h \times n_x nt×nh×nx 的张量, 其中 t t t 是双向 (下去再上来) 走时, h h h 是 (水平) 偏移量, x x x 是 CMP 中心点的位置.
相关文章:
)
论文笔记: 深度学习速度模型构建的层次迁移学习方法 (未完)
摘要: 分享对论文的理解, 原文见 Jrome Simon, Gabriel Fabien-Ouellet, Erwan Gloaguen, and Ishan Khurjekar, Hierarchical transfer learning for deep learning velocity model building, Geophysics, 2003, R79–R93. 这次的层次迁移应该指从 1D 到 2D 再到 3D. 摘要 深…...

苹果为 Vision Pro 头显申请游戏手柄专利
苹果Vision Pro 推出后,美国专利局公布了两项苹果公司申请的游戏手柄专利,其中一项的专利图如下图所示。据 PatentlyApple 报道,虽然申请专利并不能保证苹果公司会推出游戏手柄,但是苹果公司同时也为游戏手柄申请了商标࿰…...

【数据结构】多叉树转换为二叉树-c++代码实现-POJ 3437 Tree Grafting
文章目录 写这个题目的原因寻找提交网址题目解决思路AC代码成功AC 写这个题目的原因 1、今天在看王道考研数据结构的课(虽然我要保研,但是因为这些看保研面试的时候会问,所以看一下嘞orz),看到了这个多叉树转换为二叉…...
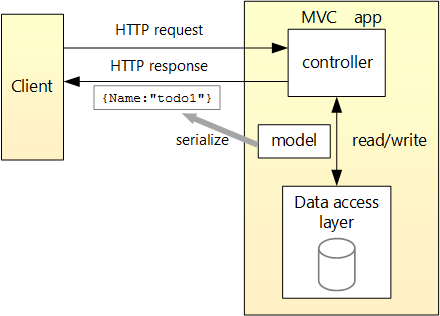
ASP.NET Core 中基于 Controller 的 Web API
基于 Controller 的 Web API ASP.NET Wep API 的请求架构 客户端发送Http请求,Contoller响应请求,并从数据库读取数据,序列化数据,然后通过 Http Response返回序列化的数据。 ControllerBase 类 Web API 的所有controllers 一般…...
iOS系统修复软件 Fix My iPhone for Mac
Fix My iPhone for Mac是一款iOS系统恢复工具。修复您的iPhone卡在Apple徽标,黑屏,冻结屏幕,iTunes更新/还原错误和超过20个iOS 12升级失败。这个macOS桌面应用程序提供快速,即时的解决方案来修复您的iOS系统问题,而不…...

Git企业开发控制理论和实操-从入门到深入(七)|企业级开发模型
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

15. 卡牌游戏
目录 题目 思路 C整体代码(含详细注释) 题目 Description 小张在玩一种卡牌游戏,牌组由张牌组成,其中张上写有数字各一张,其余张上全部是数字。 现在牌组经过随机打乱后,小张拿走其中张牌作为手牌&#…...
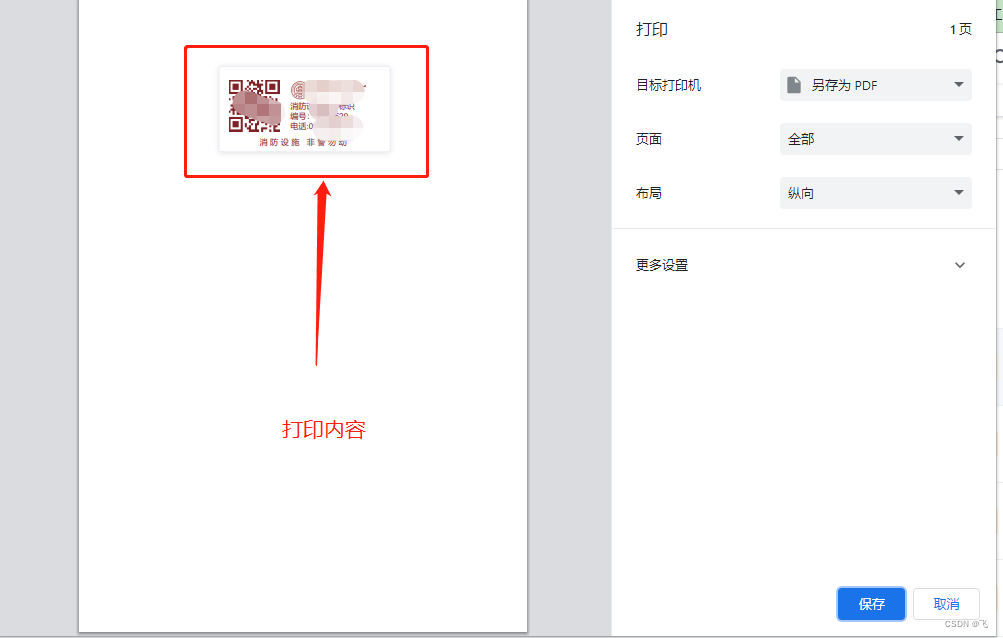
vue使用打印组件print-js
项目场景: 由于甲方要求,项目需要打印二维码标签,故开发此功能 开发流程 安装包:npm install print-js --saveprint-js的使用 <template><div id"print" ref"print" ><p>打印内容<p&…...

20230830比赛总结
分数 预估分数: 100 100 [ 0 , 20 ] 100 [ 300 , 320 ] 100100[0,20]100[300,320] 100100[0,20]100[300,320] 实际分数: 100 100 10 100 310 10010010100310 10010010100310 反思 B 只是粗略观察表就急于写决策单调性优化,写完后…...
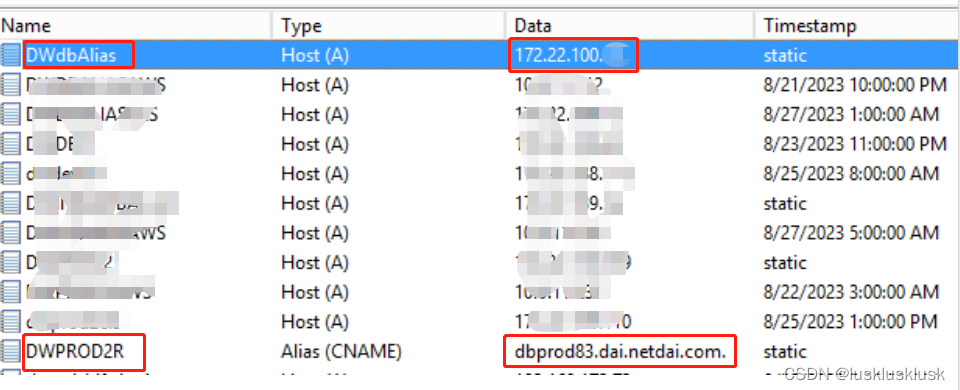
DNS指向别名还是IP
现在有一台服务器dbprod126,ip是172.22.100.4 现在有一个需求,需要在dns中对dbprod126建一个别名wondadb3r的记录,也就是ping wondadb3r的时候显示的是dbprod126的ip,目前有两种方法,主要使用方法1指向别名…...

【考研数学】概率论与数理统计 —— 第二章 | 一维随机变量及其分布(1,基本概念与随机变量常见类型)
文章目录 引言一、一维随机变量及其分布1.1 随机变量1.2 分布函数 二、随机变量常见类型及分布2.1 离散型随机变量2.2 连续型随机变量及概率密度函数 写在最后 引言 暑假接近尾声了,争取赶一点概率论部分的进度。 一、一维随机变量及其分布 1.1 随机变量 设随机试…...
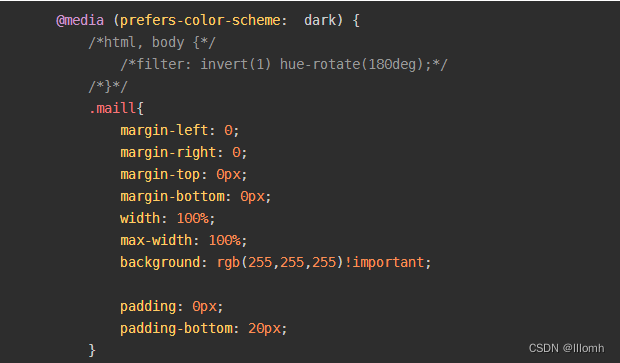
CSS判断手机暗黑模式
手机有个功能到了晚上会自动变成深色也就是暗黑模式.这种情况下网页会自动变颜色.如果想自由控制暗黑模式下的html样式的话,可以用如下方式: media (prefers-color-scheme: dark) {/*html, body {*//*filter: invert(1) hue-rotate(180deg);*//*}*/.maill{margin-left: 0;marg…...
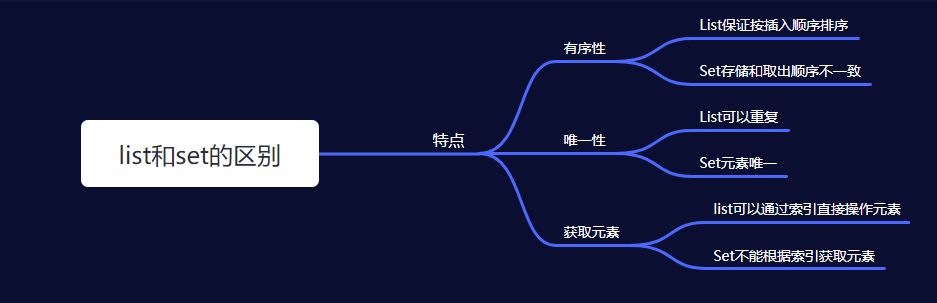
【java中的Set集合】HashSet、LinkedHashSet、TreeSet(最通俗易懂版!!)
目录 一、HashSet集合 1.HashSet集合的特点 2.HashSet常用方法 二、LinkedHashSet集合 LinkedHashSet集合的特点 三、TreeSet集合 1.TreeSet集合的特点 2.TreeSet的基本使用 四、HashSet、LinkedHashSet、TreeSet的使用场景 五、list和set集合的区别 一、HashSet集合 …...

python中的文件操作
我们平常对文件的基本操作,大概可以分为三个步骤(简称文件操作三步走): ① 打开文件 ② 读写文件 ③ 关闭文件 【注意事项】 注意:可以只打开和关闭文件,不进行任何读写 文件打开 open函数ÿ…...

spark支持深度学习批量推理
背景 在数据量较大的业务场景中,spark在数据处理、传统机器学习训练、 深度学习相关业务,能取得较明显的效率提升。 本篇围绕spark大数据背景下的推理,介绍一些优雅的使用方式。 spark适用场景 大数据量自定义方法处理、类sql处理传统机器…...

代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性 做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。 1 300. 最长递增子序列 300. 最长递增子序列 AC: class Solution { public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] max(dp[j],dp[i] …...

gcc4.8.5升级到gcc4.9.2
第1步:获取repo [rootlocalhost SPECS]# wget --no-check-certificate https://copr.fedoraproject.org/coprs/rhscl/devtoolset-3/repo/epel-6/rhscl-devtoolset-3-epel-6.repo -O /etc/yum.repos.d/devtoolset-3.repo --2021-12-07 20:53:26-- https://copr.fedo…...
:常用函数)
Golang 中的 archive/zip 包详解(三):常用函数
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便,本文讲解下常用函数。 zip.OpenReader 定义如下: func OpenReader(name string) (*R…...

微服务架构七种模式
微服务架构七种模式 目录概述需求: 设计思路实现思路分析 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.…...
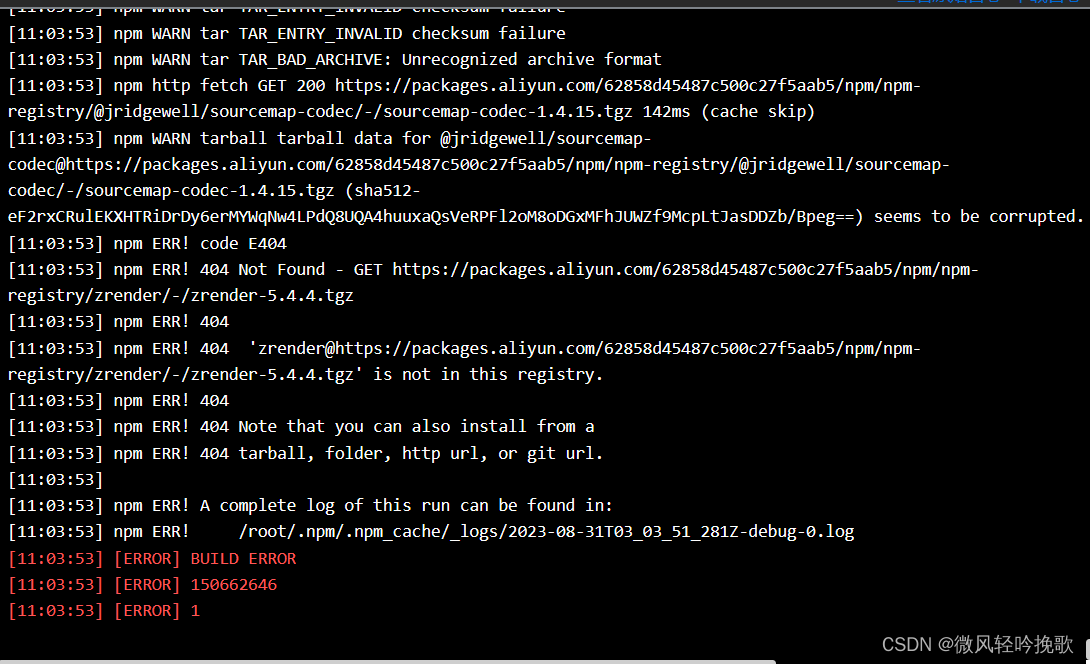
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
