深入探讨梯度下降:优化机器学习的关键步骤(二)
文章目录
- 🍀引言
- 🍀eta参数的调节
- 🍀sklearn中的梯度下降
🍀引言
承接上篇,这篇主要有两个重点,一个是eta参数的调解;一个是在sklearn中实现梯度下降
在梯度下降算法中,学习率(通常用符号η表示,也称为步长或学习速率)的选择非常重要,因为它直接影响了算法的性能和收敛速度。学习率控制了每次迭代中模型参数更新的幅度。以下是学习率(η)的重要性:
-
收敛速度:学习率决定了模型在每次迭代中移动多远。如果学习率过大,模型可能会在参数空间中来回摇摆,导致不稳定的收敛或甚至发散。如果学习率过小,模型将收敛得很慢,需要更多的迭代次数才能达到最优解。因此,选择合适的学习率可以加速收敛速度。
-
稳定性:过大的学习率可能会导致梯度下降算法不稳定,甚至无法收敛。过小的学习率可以使算法更加稳定,但可能需要更多的迭代次数才能达到最优解。因此,合适的学习率可以在稳定性和收敛速度之间取得平衡。
-
避免局部最小值:选择不同的学习率可能会导致模型陷入不同的局部最小值。通过尝试不同的学习率,您可以更有可能找到全局最小值,而不是被困在局部最小值中。
-
调优:学习率通常需要调优。您可以尝试不同的学习率值,并监视损失函数的收敛情况。通常,您可以使用学习率衰减策略,逐渐降低学习率以改善收敛性能。
-
批量大小:学习率的选择也与批量大小有关。通常,小批量梯度下降(Mini-batch Gradient Descent)使用比大批量梯度下降更大的学习率,因为小批量可以提供更稳定的梯度估计。
总之,学习率是梯度下降算法中的关键超参数之一,它需要仔细选择和调整,以在训练过程中实现最佳性能和收敛性。不同的问题和数据集可能需要不同的学习率,因此在实践中,通常需要进行实验和调优来找到最佳的学习率值。
🍀eta参数的调节
在上代码前我们需要知道,如果eta的值过小会造成什么样的结果
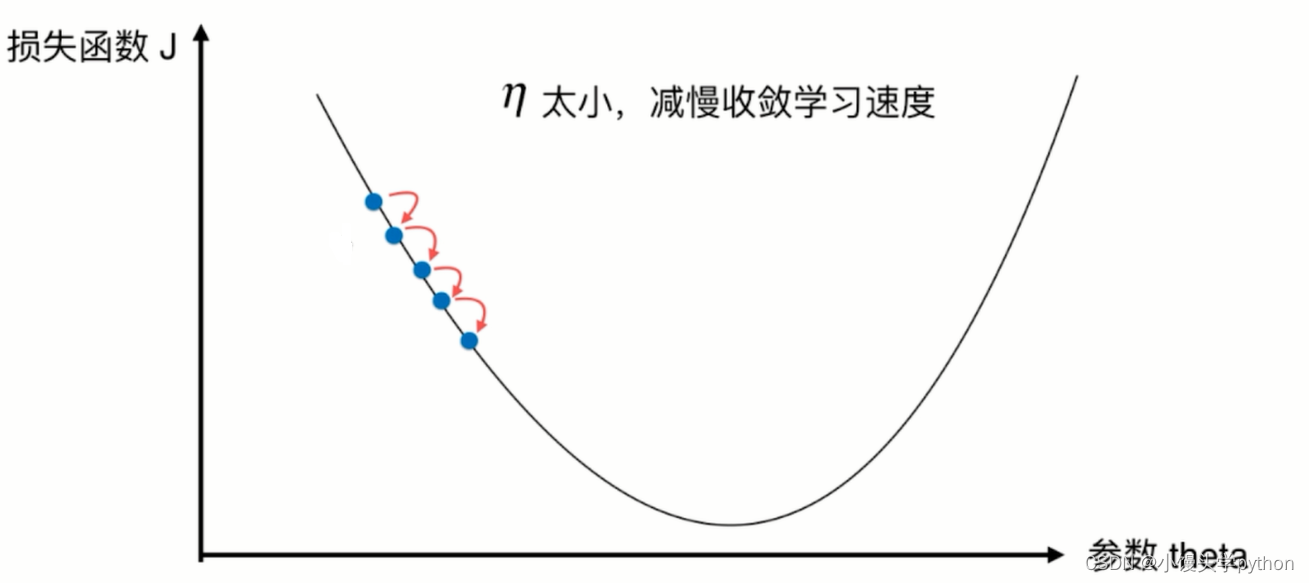
反之如果过大呢
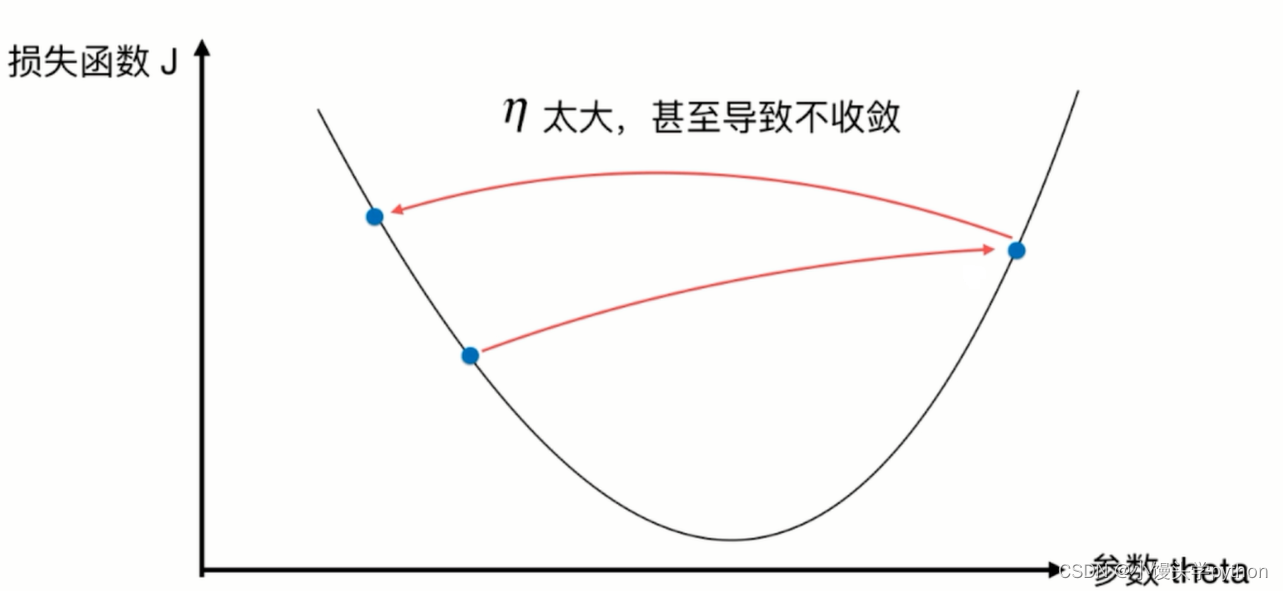
可见,eta过大过小都会影响效率,所以一个合适的eta对于寻找最优有着至关重要的作用
在上篇的学习中我们已经初步完成的代码,这篇我们将其封装一下
首先需要定义两个函数,一个用来返回thera的历史列表,一个则将其绘制出来
def gradient_descent(eta,initial_theta,epsilon = 1e-8):theta = initial_thetatheta_history = [initial_theta]def dj(theta): return 2*(theta-2.5) # 传入theta,求theta点对应的导数def j(theta):return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值while True:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta theta_history.append(theta)if np.abs(j(theta)-j(last_theta))<epsilon:breakreturn theta_historydef plot_gradient(theta_history):plt.plot(plt_x,plt_y)plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')plt.show()
其实就是上篇代码的整合罢了
之后我们需要进行简单的调参了,这里我们分别采用0.1、0.01、0.9,这三个参数进行调节
eta = 0.1
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
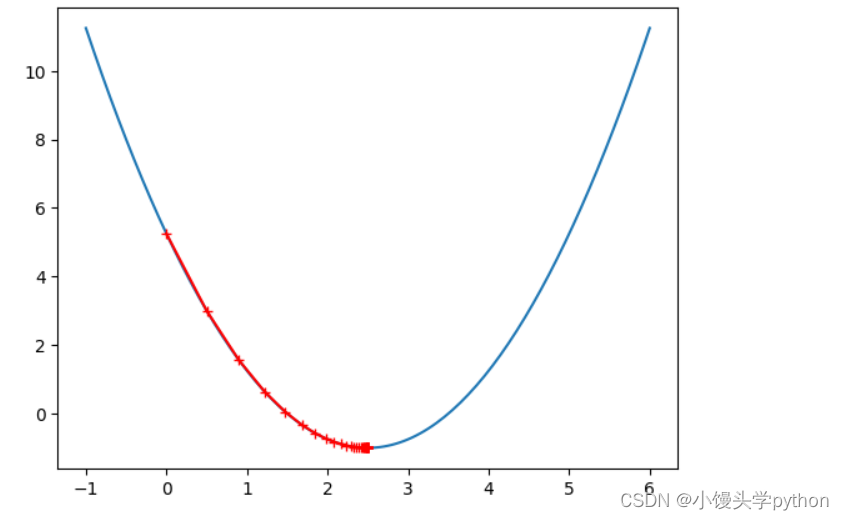
eta = 0.01
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下

eta = 0.9
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
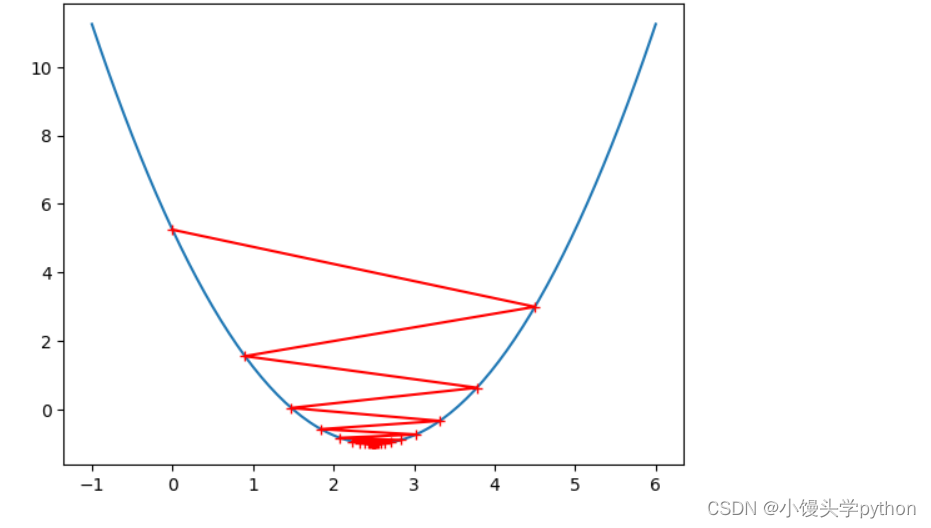
这三张图与之前的提示很像吧,可见调参的重要性
如果我们将eta改为1.0呢,那么会发生什么
eta = 1.0
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
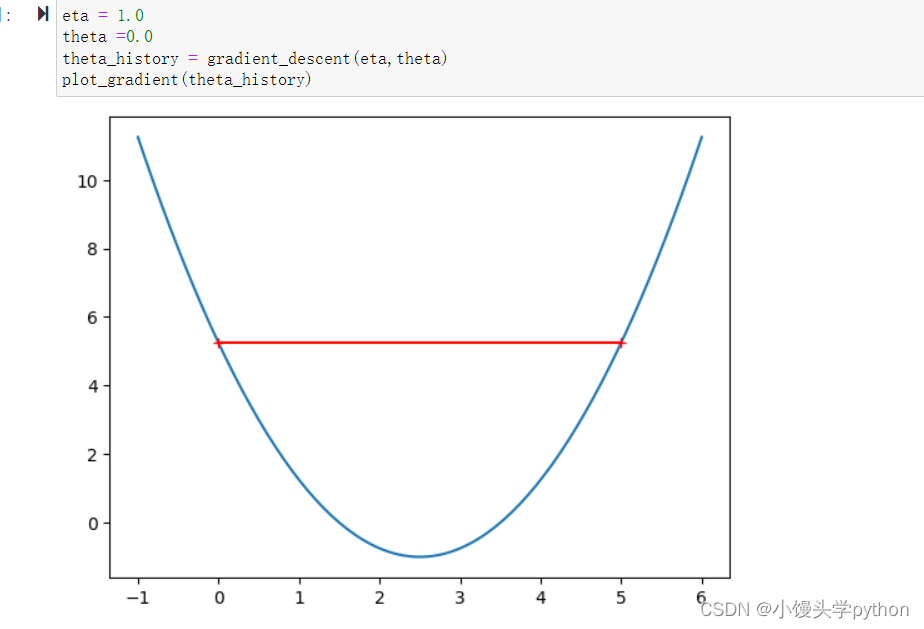
那改为1.1呢
eta = 1.1
theta =0.0
plot_gradient(gradient_descent(eta,theta))
len(theta_history)
运行结果如下
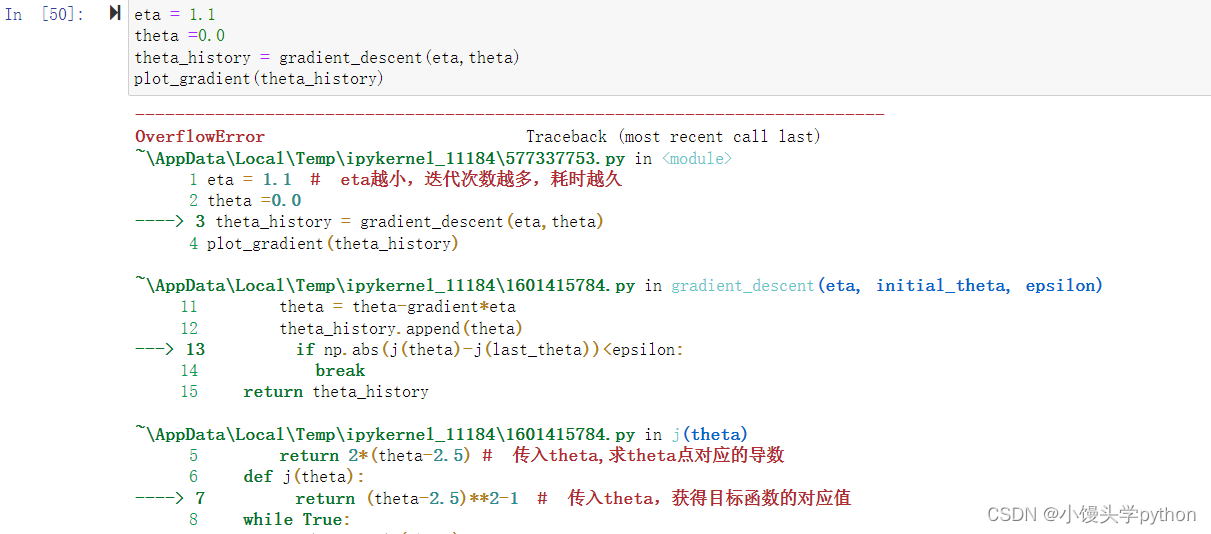
我们从图可以清楚的看到,当eta为1.1的时候是嗷嗷增大的,这种情况我们需要采用异常处理来限制一下,避免报错,处理的方式是限制循环的最大值,且可以在expect中设置inf(正无穷)
def gradient_descent(eta,initial_theta,n_iters=1e3,epsilon = 1e-8):theta = initial_thetatheta_history = [initial_theta]i_iter = 1def dj(theta): try:return 2*(theta-2.5) # 传入theta,求theta点对应的导数except:return float('inf')def j(theta):return (theta-2.5)**2-1 # 传入theta,获得目标函数的对应值while i_iter<=n_iters:gradient = dj(theta)last_theta = thetatheta = theta-gradient*eta theta_history.append(theta)if np.abs(j(theta)-j(last_theta))<epsilon:breaki_iter+=1return theta_historydef plot_gradient(theta_history):plt.plot(plt_x,plt_y)plt.plot(theta_history,[(i-2.5)**2-1 for i in theta_history],color='r',marker='+')plt.show()
注意:inf表示正无穷大
🍀sklearn中的梯度下降
这里我们还是以波士顿房价为例子
首先导入需要的库
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
之后取一部分的数据
boston = load_boston()
X = boston.data
y = boston.target
X = X[y<50]
y = y[y<50]
然后进行数据归一化
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y)
std = StandardScaler()
std.fit(X_train)
X_train_std=std.transform(X_train)
X_test_std=std.transform(X_test)
sgd_reg = SGDRegressor()
sgd_reg.fit(X_train_std,y_train)
最后取得score
sgd_reg.score(X_test_std,y_test)
运行结果如下


挑战与创造都是很痛苦的,但是很充实。
相关文章:

深入探讨梯度下降:优化机器学习的关键步骤(二)
文章目录 🍀引言🍀eta参数的调节🍀sklearn中的梯度下降 🍀引言 承接上篇,这篇主要有两个重点,一个是eta参数的调解;一个是在sklearn中实现梯度下降 在梯度下降算法中,学习率…...

高频算法面试题
合并两个有序数组 const merge (nums1, nums2) > {let p1 0;let p2 0;const result [];let cur;while (p1 < nums1.length || p2 < nums2.length) {if (p1 nums1.length) {cur nums2[p2];} else if (p2 nums2.length) {cur nums1[p1];} else if (nums1[p1] &…...
Hive-启动与操作(2)
🥇🥇【大数据学习记录篇】-持续更新中~🥇🥇 个人主页:beixi 本文章收录于专栏(点击传送):【大数据学习】 💓💓持续更新中,感谢各位前辈朋友们支持…...

css transition 指南
css transition 指南 在本文中,我们将深入了解 CSS transition,以及如何使用它们来创建丰富、精美的动画。 基本原理 我们创建动画时通常需要一些动画相关的 CSS。 下面是一个按钮在悬停时移动但没有动画的示例: <button class"…...

LeetCode 面试题 02.05. 链表求和
文章目录 一、题目二、C# 题解 一、题目 给定两个用链表表示的整数,每个节点包含一个数位。 这些数位是反向存放的,也就是个位排在链表首部。 编写函数对这两个整数求和,并用链表形式返回结果。 点击此处跳转题目。 示例: 输入&a…...

一米脸书营销软件
功能优势 JOIN ADVANTAGE HOME PAGE MARKETING 公共主页营销 可同时对多个账户公共主页评论,点赞等 可批量邀请多个好友对Facebook公共主页进行评论点赞等,也可批量登录小号对自己公共主页进行点赞。 GROUP MARKETING 小组营销 可批量针对不同账户进行…...
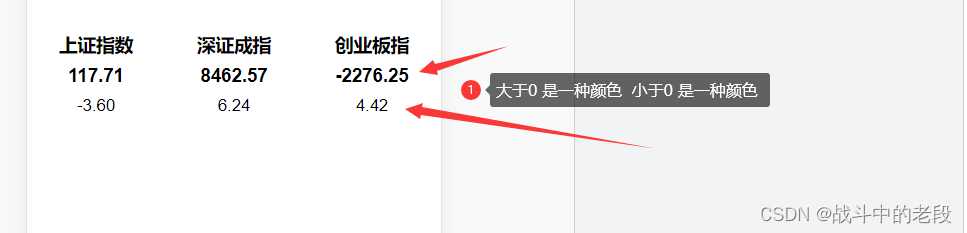
vue 根据数值判断颜色
1.首先style样式给两种颜色 用:class 三元运算符判断出一种颜色 第一步:在style里边设置两种颜色 .green{color: green; } .orange{color: orangered; }在取数据的标签 里边 判断一种颜色 :class"item.quote.current >0 ?orange: green"<van-gri…...

Hugging Face 实战系列 总目录
PyTorch 深度学习 开发环境搭建 全教程 Transformer:《Attention is all you need》 Hugging Face简介 1、Hugging Face实战-系列教程1:Tokenizer分词器(Transformer工具包/自然语言处理) Hungging Face实战-系列教程1:Tokenize…...
国标视频云服务EasyGBS国标视频平台迁移服务器后无法启动的问题解决方法
国标视频云服务EasyGBS支持设备/平台通过国标GB28181协议注册接入,并能实现视频的实时监控直播、录像、检索与回看、语音对讲、云存储、告警、平台级联等功能。平台部署简单、可拓展性强,支持将接入的视频流进行全终端、全平台分发,分发的视频…...

HTML <th> 标签
实例 普通的 HTML 表格,包含两行两列: <table border="1"><tr><th>Company</th><th>Address</th></tr><tr><td>Apple, Inc.</td><td>1 Infinite Loop Cupertino, CA 95014</td></tr…...

HTTP/1.1协议中的响应报文
2023年8月30日,周三下午 目录 概述响应报文示例详述 概述 HTTP/1.1协议的响应报文由以下几个部分组成: 状态行(Status Line)响应头部(Response Headers)空行(Blank Line)响应体&a…...

TDengine函数大全-选择函数
以下内容来自 TDengine 官方文档 及 GitHub 内容 。 以下所有示例基于 TDengine 3.1.0.3 TDengine函数大全 1.数学函数 2.字符串函数 3.转换函数 4.时间和日期函数 5.聚合函数 6.选择函数 7.时序数据库特有函数 8.系统函数 选择函数 TDengine函数大全BOTTOMFIRSTINTERPLASTLAS…...

非关系型数据库Redis的安装
一、关系型数据库与非关系型数据库的区别:---------面试高频率问题 1、首先了解一下 什么是关系型数据库? 关系型数据库最典型的数据结构是表,由二维表及其之间的联系所组成的一个数据组织。 优点: 易于维护:都是使用…...

oracle 创建数据库
查询表空间的命令 select t1.name,t2.name from v$tablespace t1,v$datafile t2 where t1.ts# t2.ts#; CREATE TABLESPACE ORM_342_BETA DATAFILE /app/oracle/oradata/sysware/ORM_342_BETA.DBF size 800M --存储地址 初始大小800M autoextend on nex…...
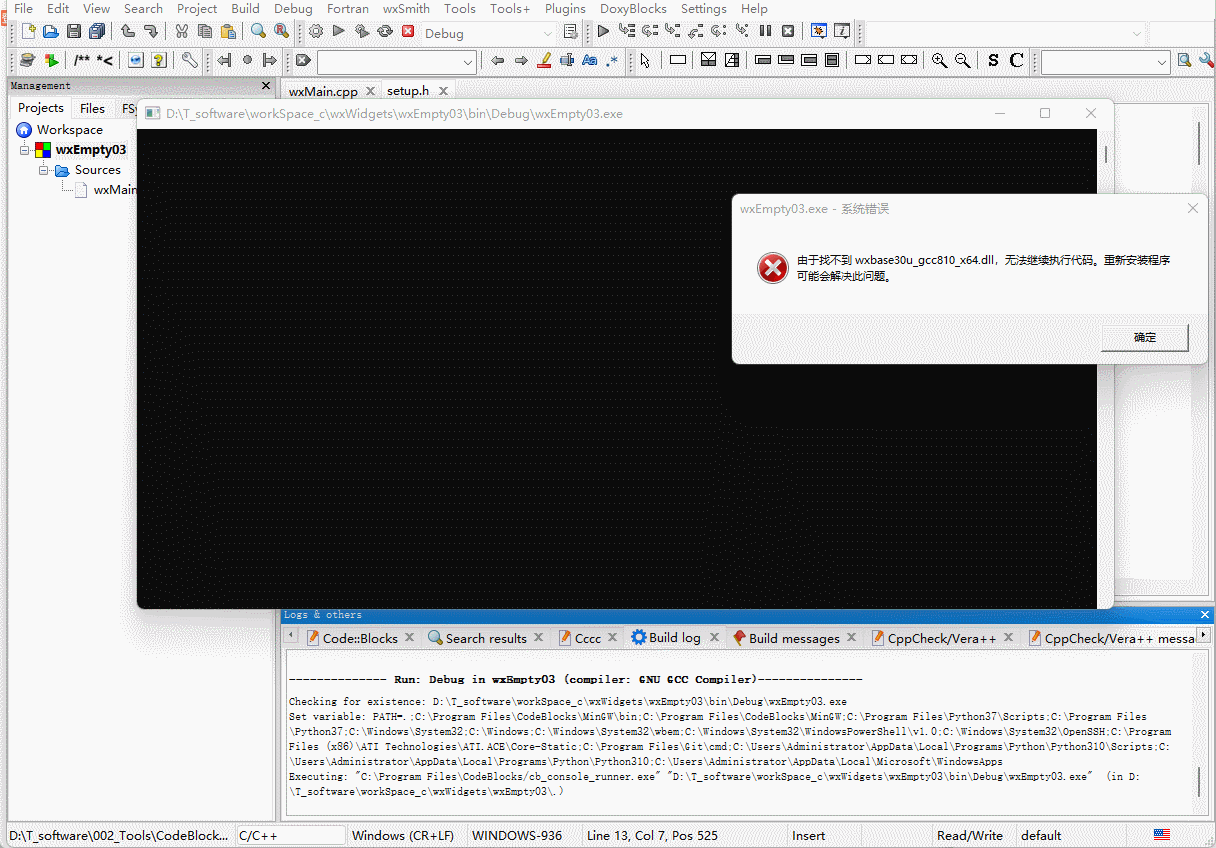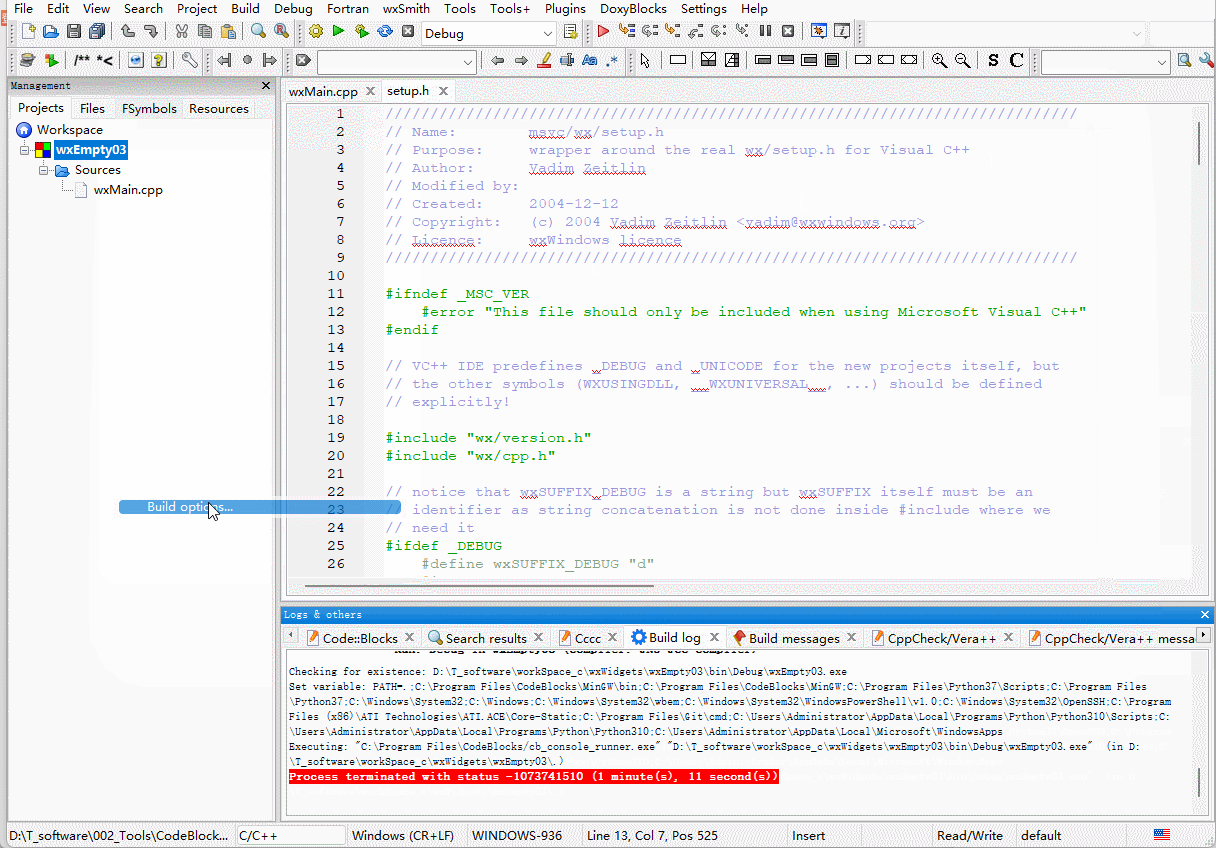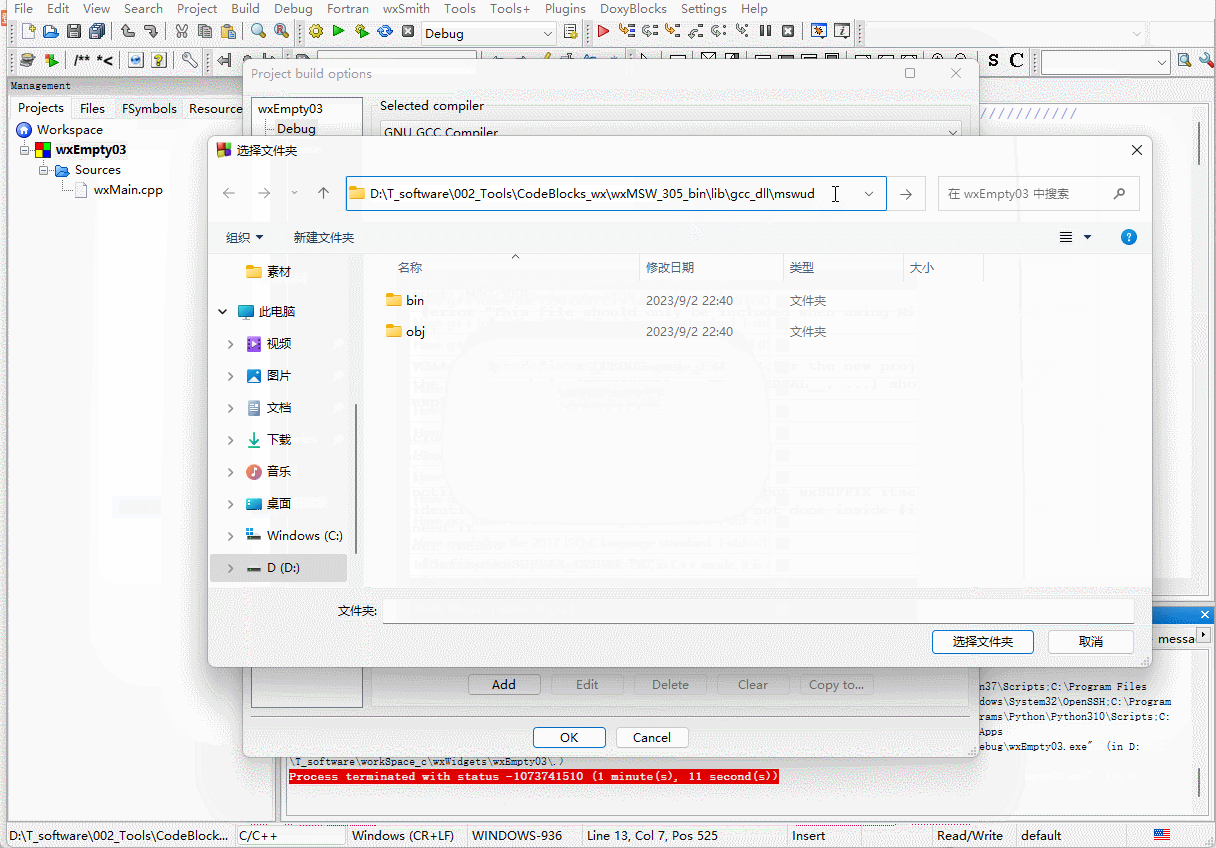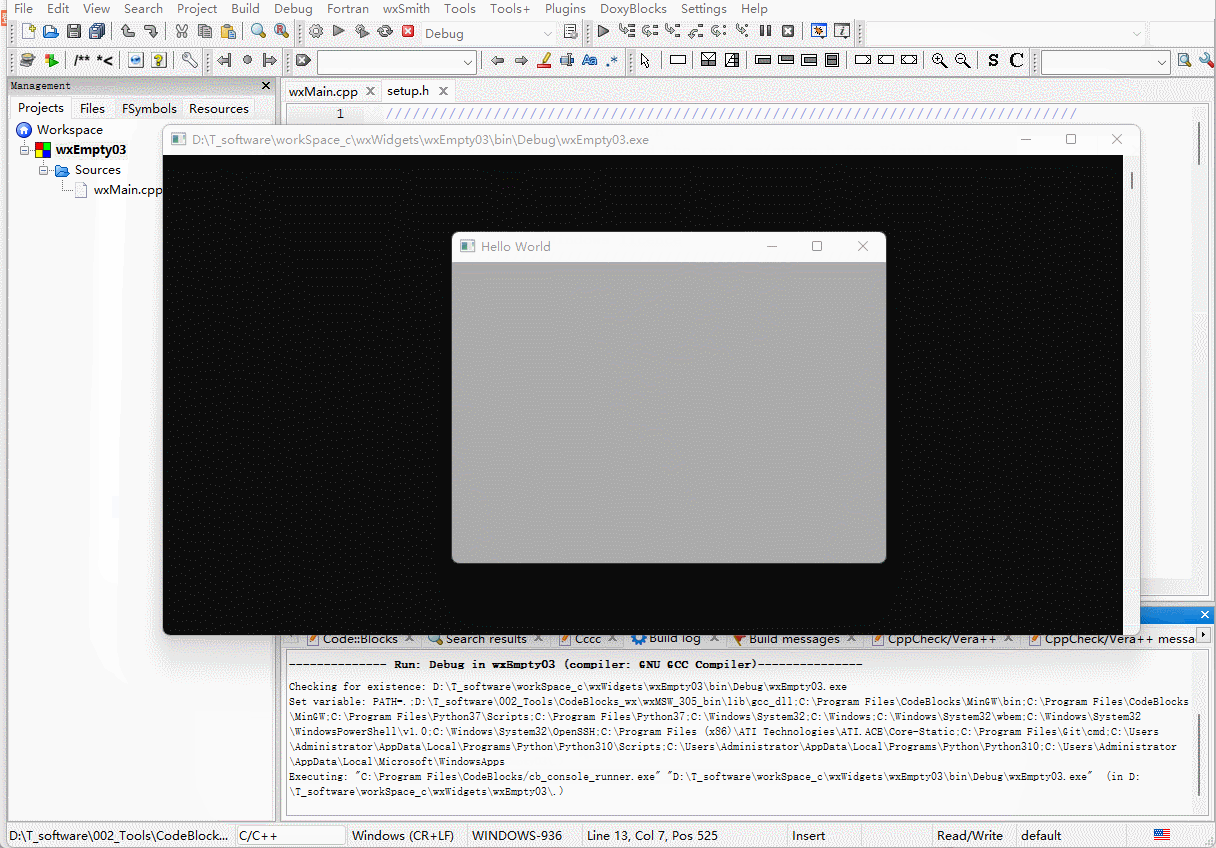
wxWidgets从空项目开始Hello World
前文回顾 接上篇,已经是在CodeBlocks20.03配置了wxWidgets3.0.5,并且能够通过项目创建导航创建一个新的工程,并且成功运行。 那么上一个是通过CodeBlocks的模板创建的,一进去就已经是2个头文件2个cpp文件,总是感觉缺…...
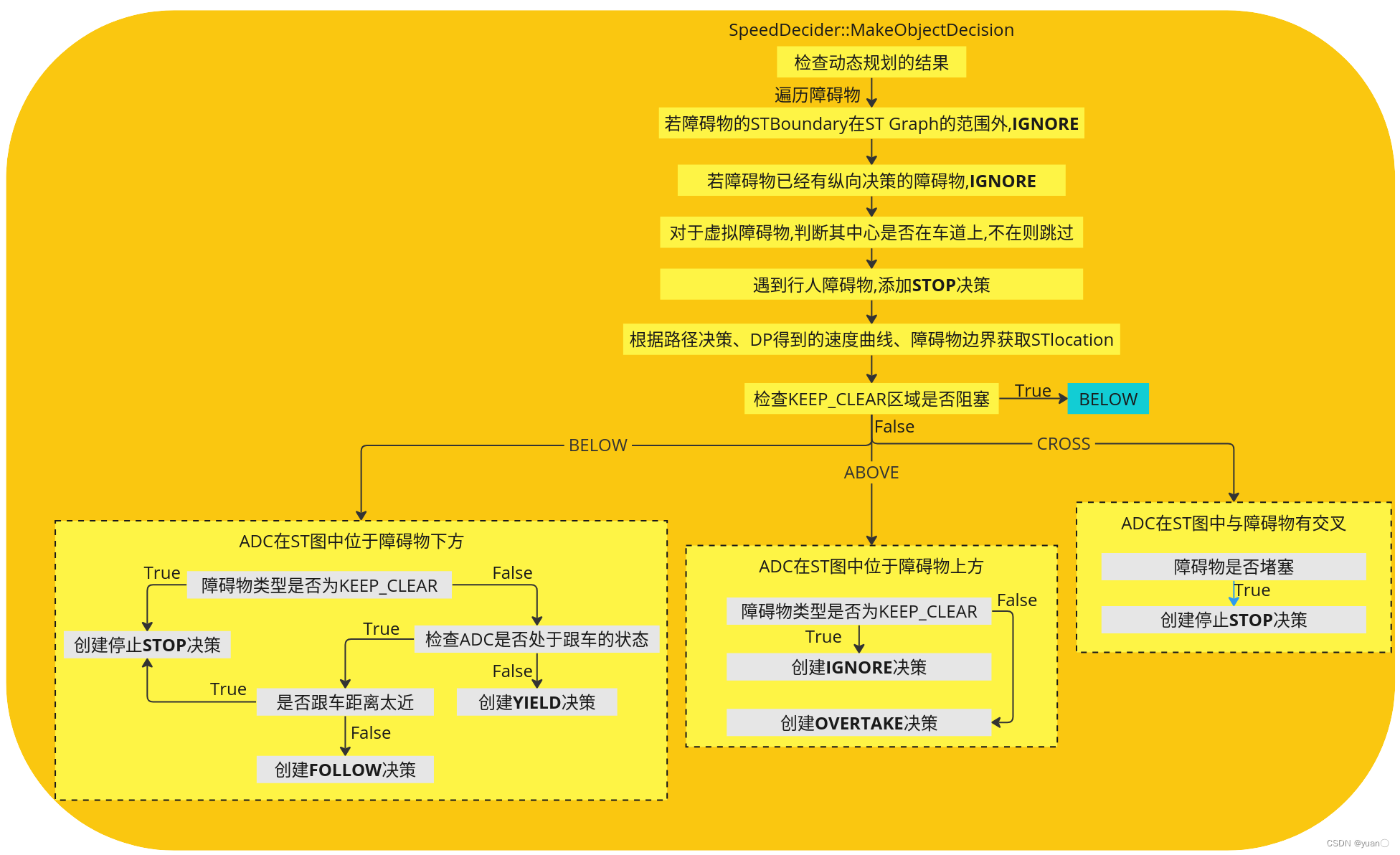
【Apollo学习笔记】——规划模块TASK之SPEED_DECIDER
文章目录 前言SPEED_DECIDER功能简介SPEED_DECIDER相关配置SPEED_DECIDER流程MakeObjectDecisionGetSTLocationCheck类函数CheckKeepClearCrossableCheckStopForPedestrianCheckIsFollowCheckKeepClearBlocked Create类函数 前言 在Apollo星火计划学习笔记——Apollo路径规划算…...
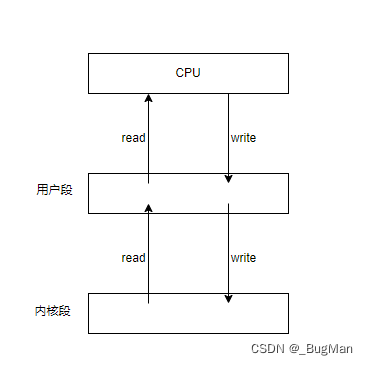
【操作系统】一文快速入门,很适合JAVA后端看
作者简介: 目录 1.概述 2.CPU管理 3.内存管理 4.IO管理 1.概述 操作系统可以看作一个计算机的管理系统,对计算机的硬件资源提供了一套完整的管理解决方案。计算机的硬件组成有五大模块:运算器、控制器、存储器、输入设备、输出设备。操作…...

C++ Primer阅读笔记--allocator类的使用
1--allocator类的使用背景 new 在分配内存时具有一定的局限性,其将内存分配和对象构造组合在一起;当分配一大块内存时,一般希望可以在内存上按需构造对象,这时需要将内存分配和对象构造分离,而定义在头文件 memory 的 …...
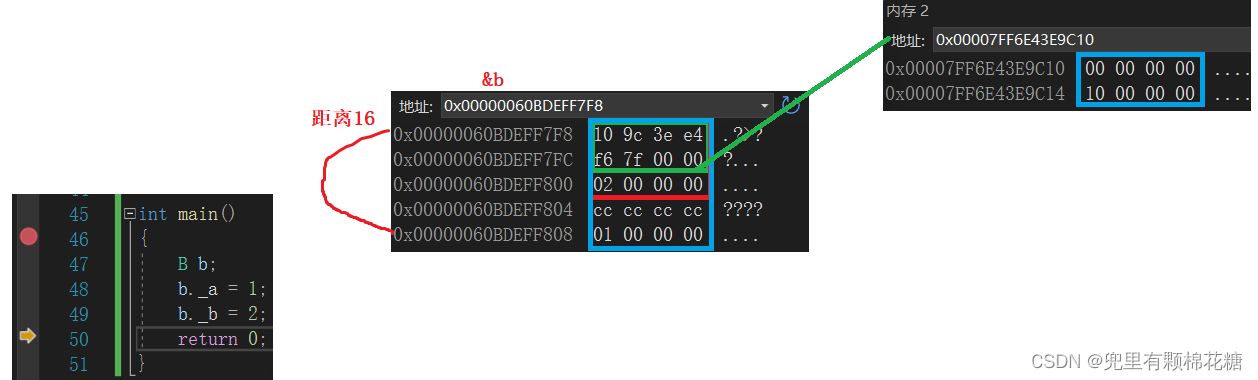
【C++历险记】面向对象|菱形继承及菱形虚拟继承
个人主页:兜里有颗棉花糖💪 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【C之路】💌 本专栏旨在记录C的学习路线,望对大家有所帮助🙇 希望我们一起努力、成长&…...
【Locomotor运动模块】攀爬
文章目录 一、攀爬主体“伪身体”1、“伪身体”的设置2、“伪身体”和“真实身体”,为什么同步移动3、“伪身体”和“真实身体”,碰到墙时不同步的原因①现象②原因③解决 二、攀爬1、需要的组件:“伪身体”、Climbing、Climbable及Interacto…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
