圆角矩形的绘制和曲线均匀化

摘要： 圆角矩形是软件 UI 等视觉设计中的常见表达，一种常见的绘制方法是将矩形的四角替换为与边相切的四分之一圆弧，然而这种绘制方式会在连接处产生视觉上的切折感，这是因为圆弧和直线的连接处只满足 $G^1$ 连续性。本文探究了如何使用高次埃米尔特插值绘制高阶连续的圆角曲线，以及如何使用常微分方程的数值解法实现曲线的均匀化。
关键词： 圆角矩形；埃米尔特插值；常微分方程数值解

---

引言

圆角矩形被广泛应用于产品的视觉设计中，例如智能手机的边框、移动应用的图标、家具的边角等等。人们通常将在矩形的四角改为相切的四分之一圆弧来绘制圆角矩形，如图 1a 所示，在和更高阶连续曲线的对比之下，这种方法绘制出的圆角就会在连接处产生切折感，显得不是那么顺滑，原因是这种绘制方式在圆角的连接处只能满足 $G^1$ 连续，图 1b 直观展示了连接处的曲率突变。这种视觉效果的差别已经被 Apple 公司的视觉设计师注意到，并且成功应用于他们的产品设计中，例如 iOS 7 之后的图标边框抛弃了 圆弧和切线（图 2）。

图1(a)：效果对比	图1(b)：曲率图

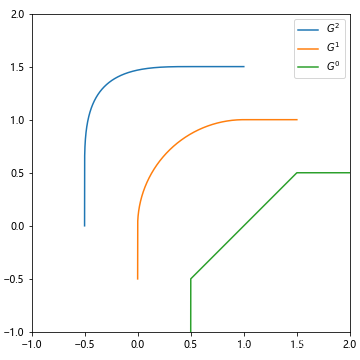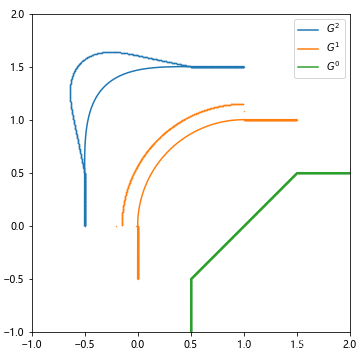图2

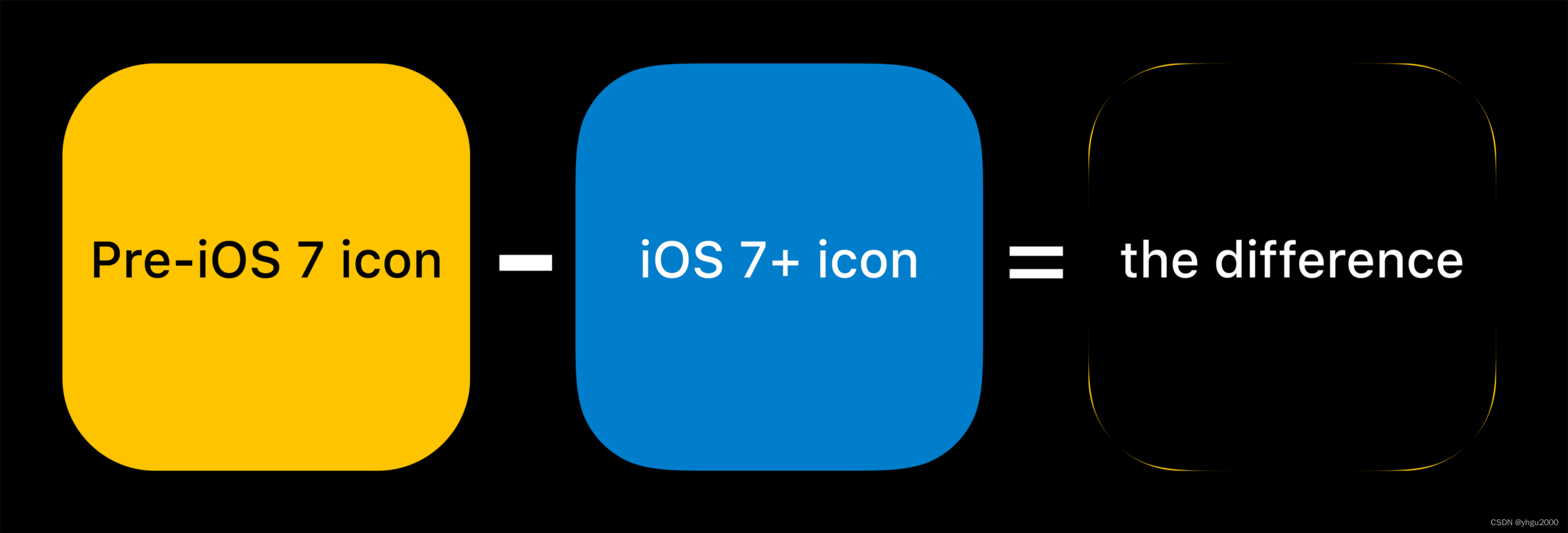根据数值分析的内容，通过埃米尔特插值可以构造任意高阶的多项式，从而可以满足任意高阶的连续性要求，所以我们就可以将其应用于圆角的绘制，从而得到更顺滑的圆角曲线。

---

问题建模

由于二维曲线上可能存在相同横坐标的点，所以一般情况下不能用形如 $y=f(x)$ 这样的函数表达，我们可以通过引入一个隐变量 $t$ 来表达任意的二维曲线：
$$\begin{array}{c}\{\begin{array}{c}{P}_x=x(t)\\ P_y=y(t)\end{array}\end{array}$$
隐变量 $t$ 可以理解为绘制过程的时间，因此公式实际上也描述了曲线的画法：对指定的时间点 $t$，可以求得要绘制的点 $P=(P_x,P_y)=(x(t),y(t))$。 例如图 1a 中的圆弧和切线组合可以表达为：
$$\begin{array}{c}P=\{\begin{array}{ll}(0,t)& t<0\\ (1-\cos (\frac{\pi }{2}t),\sin (\frac{\pi }{2}t))& 0\le t<1\\ (t,1)& 1\le t\end{array}\end{array}$$

在数学上，$x(t)$ 和 $y(t)$ 的 $k$ 阶导数连续被称为参数连续性， 使用 $C^k$ 来表示。然而参数连续性并不能完全表达曲线的连续性，因为相同
的轨迹可能由完全不同的运动过程形成，例如下面的公式和式 2 描述了同样的轨迹，但不满足 $C^1$ 连续性：
$$\begin{array}{c}P=\{\begin{array}{ll}(0,t)& t<0\\ (1-\cos (\frac{\pi }{2}t),\sin (\frac{\pi }{2}t))& 0\le t<1\\ (1,1)& 1\le t<2\\ (t-1,1)& 2\le t\end{array}\end{array}$$

因此，几何连续性（$G^k$）的概念被提出，其含义是位置 $P=(x(t),y(t))$ 关于路程 $s={\int }_0^t\sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)}\mathrm{d}t$
的参数方程（称为自然参数方程）满足 $k$ 阶导数 连续的要求。一般来说，如果一个曲线 $P=(x(t),y(t))$ 可以经过一个重参数化过程 $P=(x(t(s)),y(t(s)))$ 变成 $k$ 阶参数连续的，那么它就是 $k$ 阶几何连续的。如果 $x(t)$ 和 $y(t)$ 都是满足 $C^k$ 的多项式，那么根据经验易知，我们总可以经过一个非线性的时间放缩过程得到其对应的自然参数方程，因而它也是满足 $G^k$ 的。

不失一般性，下面我们只讨论从 $(0,0)$ 到 $(1,1)$ 的圆角绘制问题，并且不妨限定转角的绘制时间为 $[0,1]$。在这个问题中，$x(t)$ 和 $y(t)$ 要满足以下约束：

1. 起终点位置
   $$\begin{array}{c}x(0)=0,y(0)=0,x(1)=1,y(1)=1\end{array}$$

2. $G^1$ 连续
   圆角的起点和终点都与直线相接：
   $$\begin{array}{c}{x}^{\prime }(0)=0,y^{\prime }(0)=k_y,x^{\prime }(1)=k_x,y^{\prime }(1)=0\end{array}$$
   式中出现 $k_y$ 和 $k_x$ 的原因是直线 $L=(at,bt)$ 乘上一个系数后的结果 $L^{\prime }=(k\cdot at,k\cdot bt)$ 形成的图像与此前相同（即对应同样的自然参数方程）。

3. $G^n(n>1)$ 连续
   在曲线内部，$n$ 阶多项式本身即满足 $G^n$ 的要求。在端点处，因为直线二阶以上的导数都为 $0$，所以：
   $$\begin{array}{c}{x}^{(n)}(0)=y^{(n)}(0)=x^{(n)}(1)=y^{(n)}(1)=0\end{array}$$

4. 关于角平分线对称
   绘制的圆角应该关于角的平分线 $x+y=1$ 对称：
   $$\begin{array}{c}\forall t\in [0,1],\exists t^{\prime }\in [0,1]\{\begin{array}{rl}& \frac{x(t)+x(t^{\prime })}{2}+\frac{y(t)+y(t^{\prime })}{2}=1\\ & y(t^{\prime })-y(t)=x(t^{\prime })-x(t)\end{array}\end{array}$$

---

圆角的绘制

我们可以通过一个更严格的充分条件保证我们设计的函数一定满足约束 4：让绘制过程也关于这条直线对称的， 即 $t^{\prime }=1-t$，那么我们就可以推出：
$$\begin{array}{c}\begin{array}{rl}y(t)& =1-x(1-t)\\ k_y& =k_x\end{array}\end{array}$$
现在，我们只需确定 $x(t)$ 和 $k_x$ 即可，这极大简化了设计工作。设计满足约束 1-3 的函数 $x(t)$ 本质上是一个插值问题，满足 $G^n$
的圆角曲线有 $2n+2$ 个插值条件，因此可以用 $2n+1$ 次埃米尔特插值构造 $x(t)$。

以 $n=2$ 为例，构造均差表 1a，可得插值多项式：
$$\begin{array}{c}\begin{array}{r}x(t)=t^3+(k_x-3)t^3(t-1)+(6-3k_x)t^3(t-1{)}^2\end{array}\end{array}$$
图 3 显示了不同 $k_x$ 取值曲线的效果，从图上可见，$k_x$ 值的选取对效果有非常重要的影响，而当 $k_x=2$ 时曲线的视觉效果最顺滑。

很难去解释为什么 $k_x=2$ 时的曲线效果最好，但观察式 9 可知 $k_x=2$ 恰好使得中最高次项系数为 0， 此时插值多项式退化为 $2n$ 次多项式，这不得不让人怀疑这不是一种巧合。我们有理由猜测，在求更高阶连续的曲线时，同样当 $k_x$ 值的选取使得最高次项系数为 0 时效果最好。

图 3

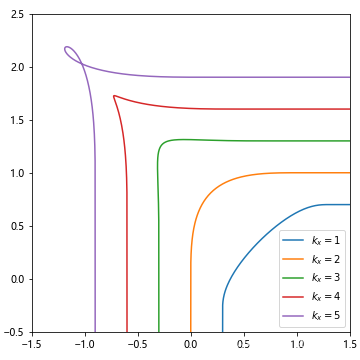顺着这个猜测会发现一个更有趣的事实：对于任意的高阶连续的曲线 $n>1$，使它们最高次项系数为 0 的条件都是
$k_x=2$！可以这样简单证明这个结论：把 $k_x=2$ 带入表 1a 得到表 1b。当 $n$ 由 2 变为 3 会多出两个插值条件，反应到均差表的构造上就是会多出表 1c 中的第 4 行和第 8 行。 在表 1b 中，第 3 行的插值条件往右下和第 6 行的插值条件往右的数字刚好满足"绝对值相等、正负号交替"的性质，则根据均差表的构造规则，在表 1c 中新构造出的一层也满足这个性质，最终右下角的数字一定为两个符号和绝对值相同的数的差，因此一定为 0。

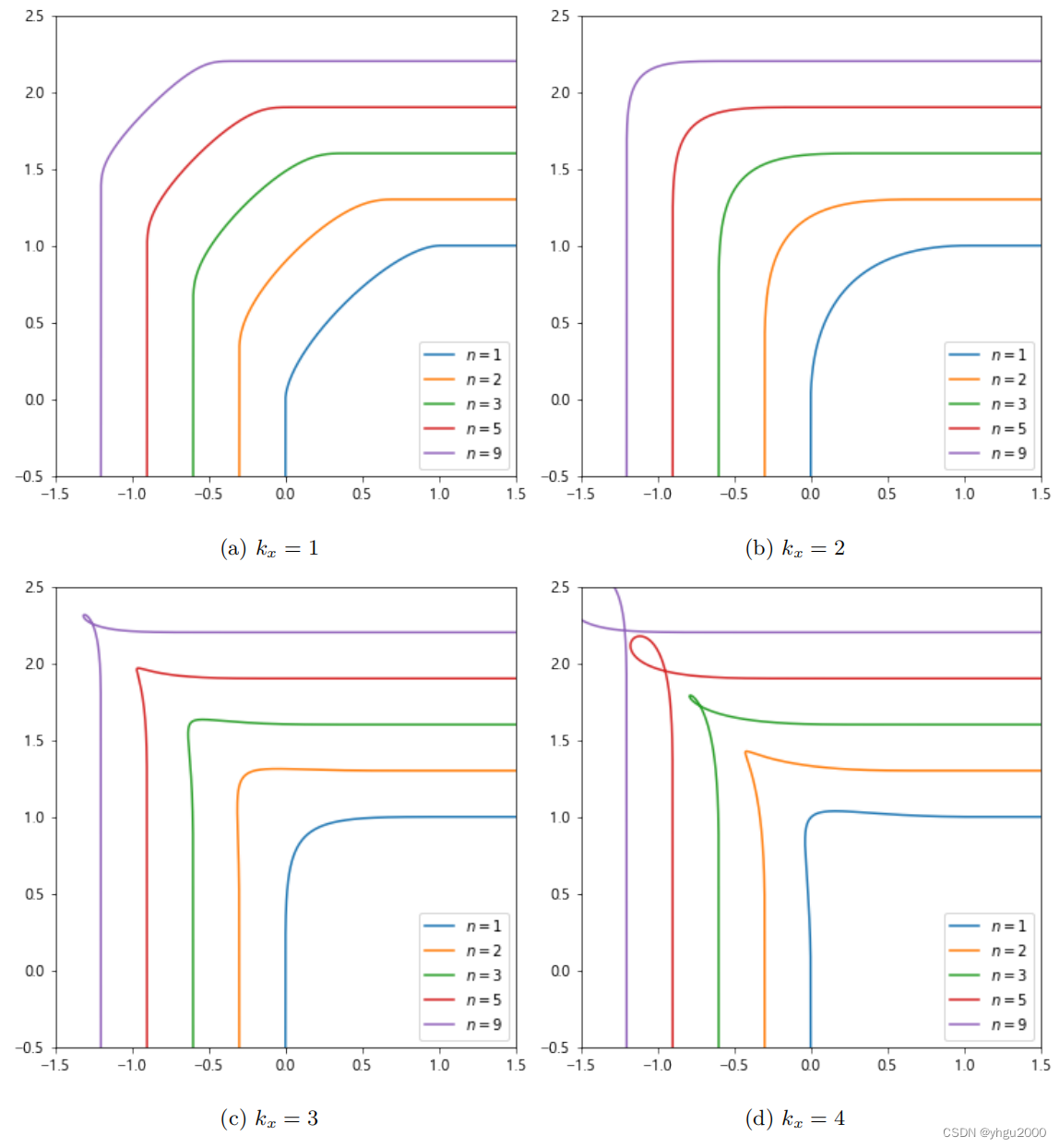
图 4 是 $n$、$k_x$ 取不同值的效果对比，可明显看出，$k_x=2$ 在任何阶次下的效果都是最好的。当可以绘制任意高阶连续的圆角之后，一个很自然的问题是：能否绘制无穷阶连续的圆角？答案是否定的，因为无穷阶连续会使得 $x(t)$ 的任意阶导数都为 0，那么根据 $x(0)=0$，使用泰勒插值可得 $x(t)\equiv 0$，这与 $x(1)=1$ 冲突。从图上也能直观看出，更高阶的曲线则产生更小的圆角，而当无穷阶连续时就会退化为直角。

图4

曲线均匀化

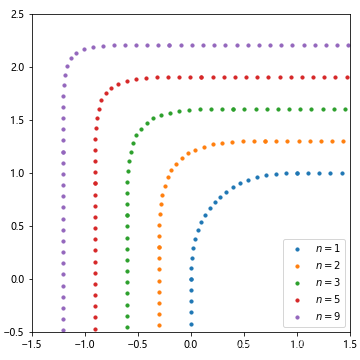
上一节给出的方法已经能让我们绘制出效果很好的连续圆角曲线了，但其仍有不足之处：所得插值公式在输入均匀的 $t$ 时输出的点是不均匀的。这个问题在绘制虚线或者点线等不连续的线时就会显露出来，如图5，点会在拐角处更集中，因此有必要继续探索将曲线均匀化的方法。

图5

本质上，曲线均匀化就是从上面一节中所得的参数方程求得对应的自然参数方程的过程。自然参数方程在大多
数情况下都很难求，无法得到解析解，只能使用数值方法，在这里也不例外。我们可以通过一个非线性的重参
数化来实现均匀化，即设计一个函数 $t(s)$，使得 $P=(x(t(s)),y(t(s)))$ 满足：
$$\begin{array}{c}\begin{array}{r}\sqrt{{\left(\frac{\mathrm{d}{P}_x}{\mathrm{d}s}\right)}^2+{\left(\frac{\mathrm{d}{P}_y}{\mathrm{d}s}\right)}^2}=1\end{array}\end{array}$$
将式 8 代入得：
$$\begin{array}{c}{\frac{\mathrm{d}{P}_x}{\mathrm{d}s}}^2+{\frac{\mathrm{d}{P}_y}{\mathrm{d}s}}^2={\left(x^{\prime }(t(s))\cdot t^{\prime }(s)\right)}^2+{\left(x^{\prime }(1-t(s))\cdot t^{\prime }(s)\right)}^2=1\end{array}$$
整理后，可得关于 $t(s)$ 的微分方程：
$$\begin{array}{c}{t}^{\prime }(s)=\frac{1}{\sqrt{x^{\prime 2}(t(s))+x^{\prime 2}(1-t(s))}}\end{array}$$
其中开方后的符号对曲线的最终均匀化结果没有影响，故可以取正。

针对本圆角绘制问题，该微分方程的初值条件为 $t(0)=0$。绘制均匀化圆角的完整流程如下：

1. 使用上一节的方法求出多项式 $x(t)$；
2. 求出 $x(t)$ 的导数 $x^{\prime }(t)$，很容易编程实现多项式的求导；
3. 给定步长 $s$，利用式 12 和初值条件 $t(0)=0$ 求得均匀分布的间隔为 $s$ 的点对应的 $t$ 值；
4. 将求得的 $t$ 值序列代入 $x(t)$ 和式 8，得到最终的点坐标。

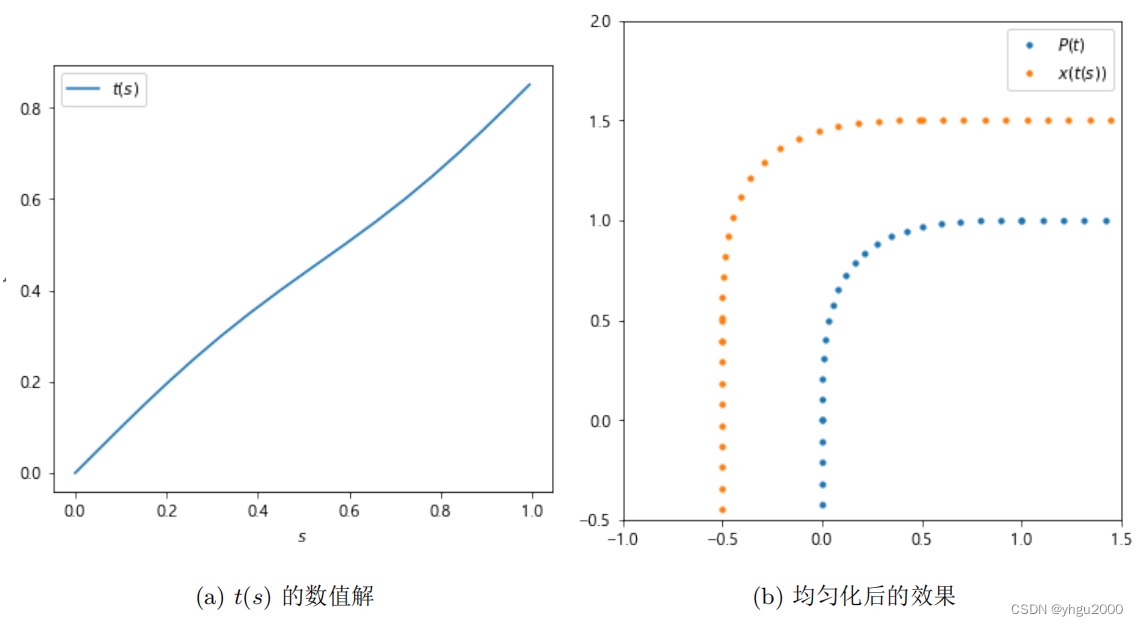
图 6b 为在 $n=2$、$k_x=2$ 的圆角曲线上取 $s=0.05$ 的绘制效果，图 6a 为对应的 $t$ 值序列，从图中可以明显看出是非线性的。

图6

---

总结

由于研究时间有限，本文只讨论了最常见的 90° 直角的绘制方法，但显然可以在本文的方法上进行一些修补使之进一步推广到任意角度。总的来说，本文基于数值分析课程内容，对圆角矩形的绘制方法进行了深入研究，成功绘制出了高阶连续的均匀圆角曲线，并通过均匀化得到了虚线版本，所得曲线相比较普通的圆弧和切线组合具有更顺滑的视觉效果。附录A展示了不同阶连续的完整矩形及点线版本的效果。

---

附录

A 完整的圆角矩形图像

B 圆角矩形绘制代码

• numalgo.py

  """埃米尔特插值实现
  """import numpy as np
  from typing import Callableclass Polynomial:"""多项式函数类"""def __init__(self, a: np.ndarray) -> None:self.a = adef __call__(self, x):return self.a @ np.full_like(self.a, x) ** np.arange(0, len(self.a))def derivate(self) -> "Polynomial":"""求导一次"""return Polynomial(self.a[1:] * np.arange(1, len(self.a)))class Emmert:"""基于均差表的埃米尔特插值函数类"""def __init__(self, x: np.ndarray, y: np.ndarray) -> None:assert x.shape == y.shapeself.x = xself.y = ydef __call__(self, x):x = x - self.xfor i in range(1, len(x)):x[i] *= x[i - 1]x[1:] = x[:-1]x[0] = 1return self.y @ xdef to_polynomial(self) -> Polynomial:"""均差表转多项式"""a = np.zeros_like(self.y)b = np.zeros_like(self.y)b[0] = 1a += self.y[0] * b[0]for i in range(1, len(self.y)):b[1:] = b[:-1]b[0] = 0b[:-1] += -self.x[i - 1] * b[1:]a += self.y[i] * breturn Polynomial(a)def emmert(constraits: dict[float, list[float]]) -> Emmert:"""埃米尔特插值"""px, py = zip(*sorted(constraits.items()))indexes = [len(i) for i in py]indexes = [sum(indexes[:i]) for i in range(len(indexes) + 1)]x = np.empty(indexes[-1], dtype=np.float64)for i in range(0, len(indexes) - 1):x[indexes[i] : indexes[i + 1]] = px[i]y = np.empty_like(x)for i in range(0, len(x) - 1):for j in range(0, len(indexes) - 1):if len(py[j]) > i:y[indexes[j] + i : indexes[j + 1]] = py[j][i]# meandiffstep = i + 1y[step:] = (y[step:] - y[step - 1 : -1]) / (x[step:] - x[:-step])return Emmert(x, y)def euler(deri: Callable[[float, float], float], xs: np.ndarray, y0: float
  ) -> np.ndarray:"""欧拉法求微分方程数值解"""ans = np.empty_like(xs)ans[0] = y0for i in range(1, len(xs)):ans[i] = ans[i - 1] + (xs[i] - xs[i - 1]) * deri(xs[i - 1], ans[i - 1])return ansdef euler_range(deri: Callable[[float, float], float],x0: float,y0: float,stop: float,step: float,
  ) -> np.ndarray:"""欧拉法求微分方程数值解，均匀步长当型循环"""ans = []while y0 < stop:ans.append(y0)y0 += step * deri(x0, y0)x0 += stepreturn np.array(ans)
  

• a4_roundrect.py

  """绘制完整的圆角矩形"""import matplotlib as mpl
  import matplotlib.pyplot as plt
  import numpy as np
  import sympy as sy
  from numpy import cos, pi, sinfrom numalgo import emmert, euler_rangempl.rcParams["font.family"] = "Microsoft YaHei"fig, ax = plt.subplots(1, 1, layout="constrained")
  fig.set_size_inches(8, 10)
  ax.axis("off")
  ax.set_xlim([-8, 8]), ax.set_ylim([-11, 11])def mirror_lefttop(arr_x, arr_y):x = np.concatenate((arr_x, -arr_x[::-1], -arr_x, arr_x[::-1]))y = np.concatenate((arr_y, arr_y[::-1], -arr_y, -arr_y[::-1]))return x, y# Gn 插值
  for n in range(2, 8):pf = emmert({0: [0, 0] + [0] * (n - 1), 1: [1, 2] + [0] * (n - 1)})p0 = pf.to_polynomial()p1 = p0.derivate()tt = lambda x, y: 1 / np.sqrt(p1(y) ** 2 + p1(1 - y) ** 2)ts = np.concatenate((np.arange(-0.4, 1.3 - n * 1.5 + 0.15, -0.15)[::-1],euler_range(tt, 0, 0, 1, 0.15),np.arange(1.1, n + 0.1, 0.15),))ts0, ts1 = np.sum(ts < 0), np.sum(ts < 1)xs = ts.copy()xs[:ts0] = 0ys = ts.copy()ys[ts1:] = 1for ti in range(ts0, ts1):xs[ti] = p0(ts[ti])ys[ts0:ts1] = 1 - xs[ts1 + 1 : ts0 + 1 : -1]xs, ys = mirror_lefttop(xs - n, ys + n * 1.5 - 1.5)ax.scatter(xs, ys, 5)arr_t = np.linspace(-n * 1.5 + 0.5, n - 0.5, 1000)t0, t1 = np.sum(arr_t < 0), np.sum(arr_t < 1)arr_x, arr_y = arr_t.copy(), arr_t.copy()arr_x[:t0], arr_y[t1:] = 0, 1for ti in range(t0, t1):arr_x[ti] = p0(arr_t[ti])arr_y[t0:t1] = 1 - arr_x[t1 + 1 : t0 + 1 : -1]xs, ys = mirror_lefttop(arr_x - n - 0.5, arr_y + n * 1.5 - 1.25 + 0.5)ax.plot(xs, ys)ax.text(0,n * 1.5 + 0.1,rf"$G^{n}$",horizontalalignment="center",verticalalignment="top",fontsize=16,)# 圆形是无穷阶几何连续的
  arr_t = np.arange(0, pi * 2, 0.01)
  xs = cos(arr_t)
  ys = sin(arr_t)
  ax.plot(xs, ys)
  ax.text(0,0,r"$G^\infty$",horizontalalignment="center",verticalalignment="center",fontsize=16,
  )# G0 画圆 + 切线
  arr_t = np.linspace(-1.25, 1.5, 1000)
  t0, t1 = np.sum(arr_t < 0), np.sum(arr_t < 1)
  arr_x, arr_y = arr_t.copy(), arr_t.copy()
  arr_x[:t0], arr_y[t1:] = 0, 1t = arr_t[t0:t1]
  x = 1 - cos(t)
  arr_x[t0:t1] = x
  arr_y[t0:t1] = 1 - x[::-1]xs, ys = mirror_lefttop(arr_x - 1.5, arr_y + 1.25)
  ax.plot(xs, ys)
  ax.text(0,2.1,r"$G^1$",horizontalalignment="center",verticalalignment="top",fontsize=16,
  )fig.savefig("a4_roundrect.png")