强化学习算法总结 (1)
强化学习算法总结 (1)
1.综述
强化学习是通过与环境进行交互,来实现目标的一种计算方法。
s − a 1 − r − s ′ s - a_1 - r- s' s−a1−r−s′
1.1强化学习优化目标
p o l i c y = a r g m a x p o l i c y E ( a , s ) [ r e w a r d ( s , a ) ] policy= argmax_{policy} E_{(a,s)}[reward(s,a)] policy=argmaxpolicyE(a,s)[reward(s,a)]
强化学习的最终目标是最大化智能体策略在和环境交互中获得的reward。通过改变策略来调整智能体和环境交互数据的分布。
1.2 平衡与探索
策略告诉我们应该采取哪些动作,同时也要对新的策略进行探索。
这里引入一个概念为懊悔值,当前动作a的收益与最优结果的差距
- ϵ − g r e e d y \epsilon - greedy ϵ−greedy
策略
i f : 采样概率: 1 − ϵ a t = a e g m a x Q ( a ) e l s e : 随机策略 if:采样概率:1 - \epsilon \\ a_t = aegmaxQ(a)\\ else:\\ 随机策略 if:采样概率:1−ϵat=aegmaxQ(a)else:随机策略
但是结果来看积累的懊悔值是和和时间成正比的,因为随机拉杆的探索概率是固定的
- 上置信界法UCB
a t = a r g m a x α [ Q ( A ) ] a_t = argmax_\alpha [Q(A)] at=argmaxα[Q(A)]
- 汤普森采样
2. 马尔科夫决策过程
MDP:利用当前已知的信息就可以决定未来
采样:根据状态转移矩阵生成一个状态序列 s 1 − > s 2 − > . . . − > s n s_1 -> s_2 -> ...-> s_n s1−>s2−>...−>sn
2.1 马尔科夫奖励过程
在决策过程中加入了奖励函数r和折扣因子,形成了马尔科夫奖励过程 < S , P , r , γ > <S,P,r,\gamma> <S,P,r,γ>,状态集合,状态转移矩阵,奖励函数,折扣因子
G t = R t + γ R t + 1 . . . = ∑ γ k R t + k G_t = R_t+ \gamma R_{t+1}... = \sum \gamma^k R_{t+k} Gt=Rt+γRt+1...=∑γkRt+k
- 价值函数
V ( s ) = E [ G t ∣ S t = s ] 我们把 G t 拆开 R t + γ V ( s t + 1 ) 而后面的 E ( γ V ( s t + 1 ∣ s t = s ) ) 用状态转移函数表示 V ( s ) = r ( s ) + γ ∑ P ( s ′ ∣ s ) V ( s ′ ) V(s) = E[G_t |S_t =s]\\我们把G_t 拆开R_t +\gamma V(s_{t+1}) 而后面的E(\gamma V(s_{t+1}|s_t =s)) 用状态转移函数表示\\V(s) = r(s) +\gamma\sum P(s'|s)V(s') V(s)=E[Gt∣St=s]我们把Gt拆开Rt+γV(st+1)而后面的E(γV(st+1∣st=s))用状态转移函数表示V(s)=r(s)+γ∑P(s′∣s)V(s′)
只适用于规模比较小的马尔科夫过程计算价值函数,不然使用 MC,TD,动态规划等算法
2.2 马尔科夫决策过程
MDP;<S,A,P,r, γ \gamma γ>:这里不再使用状态转移矩阵,而是状态转移函数
- S:状态合集
- A:动作合集
- γ \gamma γ:折扣因子
- r(s,a):奖励函数,收到了s和a影响
- P(s’|s,a):状态转移函数
策略: π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a|s) = P(A_t = a| S_t =s) π(a∣s)=P(At=a∣St=s):表示当前状态下,采取这个策略a的概率。如果是一个随机策略,输出是关于动作的概率分布函数
-
状态价值函数
V π = E π [ G t ∣ S t = s ] V^{\pi} = E_{\pi}[G_t | S_t = s] Vπ=Eπ[Gt∣St=s]
当前状态下,预计未来的收益 -
动作价值函数
Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] Q^{\pi}(s,a) = E_\pi[G_t | S_t = s ,A_t =a] Qπ(s,a)=Eπ[Gt∣St=s,At=a]
在遵循当前策略下,执行动作a的收益
V π ( s ) = ∑ π ( a ∣ s ) Q π ( s , a ) V^\pi(s) = \sum\pi(a|s) Q^\pi (s,a) Vπ(s)=∑π(a∣s)Qπ(s,a)
- 贝尔曼期望方程
Q π ( s , a ) = E π [ R t + γ Q π ( s ′ , a ′ ) ∣ S t = s , A t = a ] = r ( s , a ) + γ ∑ V ( s ′ ) = r ( s , a ) + γ ∑ P ( s ′ ∣ a , s ) ∑ π ( a ′ ∣ s ′ ) Q π ( s ′ , a ′ ) Q^\pi (s,a) = E_\pi[R_t+\gamma Q^\pi(s',a')|S_t= s,A_t = a] \\= r(s,a) +\gamma\sum V(s') \\= r(s,a) +\gamma\sum P(s'|a,s)\sum \pi(a'|s')Q^\pi(s',a') Qπ(s,a)=Eπ[Rt+γQπ(s′,a′)∣St=s,At=a]=r(s,a)+γ∑V(s′)=r(s,a)+γ∑P(s′∣a,s)∑π(a′∣s′)Qπ(s′,a′)
V π ( s ) = E π [ R t + γ V π ( s ′ ) ∣ S t = s ] = ∑ π ( a ∣ s ) ( r ( s , a ) + γ ∑ P ( s ′ ∣ s , a ) V π ( s ′ ) ) V^\pi(s) = E_\pi[R_t+\gamma V^\pi(s')|S_t = s] =\\\sum\pi(a|s)(r(s,a)+\gamma\sum P(s'|s,a)V^\pi(s')) Vπ(s)=Eπ[Rt+γVπ(s′)∣St=s]=∑π(a∣s)(r(s,a)+γ∑P(s′∣s,a)Vπ(s′))
相关文章:
)
强化学习算法总结 (1)
强化学习算法总结 (1) 1.综述 强化学习是通过与环境进行交互,来实现目标的一种计算方法。 s − a 1 − r − s ′ s - a_1 - r- s s−a1−r−s′ 1.1强化学习优化目标 p o l i c y a r g m a x p o l i c y E ( a , s ) [ r e w a r d ( s , a ) ] policy ar…...
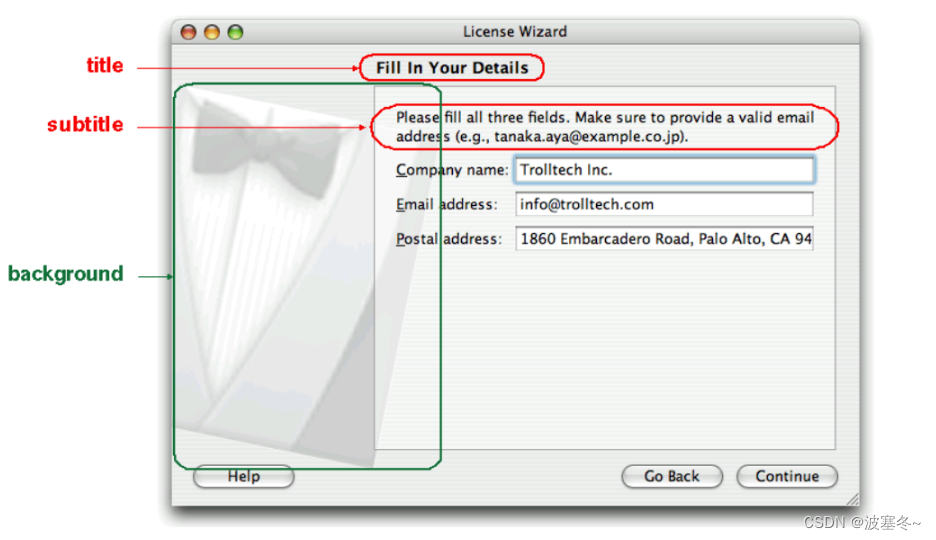
Qt应用开发(基础篇)——向导对话框 QWizard
一、前言 QWizard类继承于QDialog,为有向导界面需求的应用环境提供了一个框架。 对话框窗口 QDialog QWizard向导对话框是一个拥有队列界面的特殊对话框,向导的目的是引导用户一步一步的完成预设的流程。向导常用于软件安装界面向导、硬件线路安装向导、…...
Python类的方法
Python类的方法主要分为实例方法、类方法和静态方法三种。 1 实例方法 以self作为第一个参数的方法,就是类的实例方法。该方法由类的实例调用,Python会把调用该方法的实例对象传递给self。 如下代码定义了一个名为A的类。 class A:def __init__(self…...

变电站自动化监控系统
力安科技变电站自动化监控系统是以箱式变电站为管理对象,加装箱变网关,在完成箱变智能化改造的基础上,依托电易云,构建一体化智慧箱变及运维系统。智能箱式变电站被广泛应用于住宅小区、城市公用变压器、工厂、商场、机场、电站等…...

MySql学习笔记11——DBA命令介绍
DBA命令 数据导入 要进入Mysql 创建数据库 create database database_name;使用数据库 use database_name;初始化数据库 source .sql文件地址,不能加双引号;数据导出 要在windows的dos环境下进行 导出数据库 mysqldump database_name > 存放…...

Webpack 复习小结
nodejs学习参考 node常用命令: node xxx.js 执行js文件 npm init -y 初始化package.json npm i 软件包名 下载软件包到本地 npm i 软件包名 -g 下载软件包到全局 npm uni 软件包名 删除软件包 系统优化CDN使用 CDN for free 需求:开发模式使用本地第三…...

Laravel chunk和chunkById的坑
在编写定时任务脚本的时候,经常会用到chunk和chunkById的API。 一、前言 数据库引擎为innodb。 表结构简述,只列出了本文用到的字段。 字段类型注释idint(11)IDtypeint(11)类型mark_timeint(10)标注时间(时间戳) 索引&#x…...
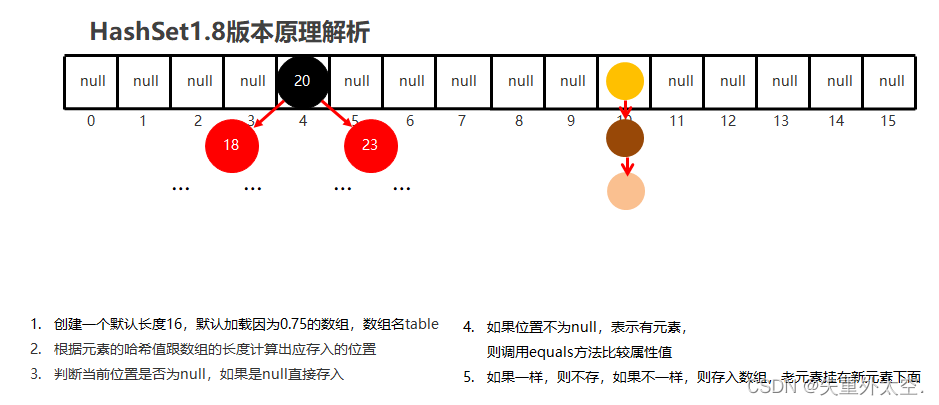
从零开始学习 Java:简单易懂的入门指南之泛型及set集合(二十二)
泛型及set集合扩展 1.泛型1.1泛型概述 2.Set集合2.1Set集合概述和特点【应用】2.2Set集合的使用【应用】 3.TreeSet集合3.1TreeSet集合概述和特点【应用】3.2TreeSet集合基本使用【应用】3.3自然排序Comparable的使用【应用】3.4比较器排序Comparator的使用【应用】3.5两种比较…...
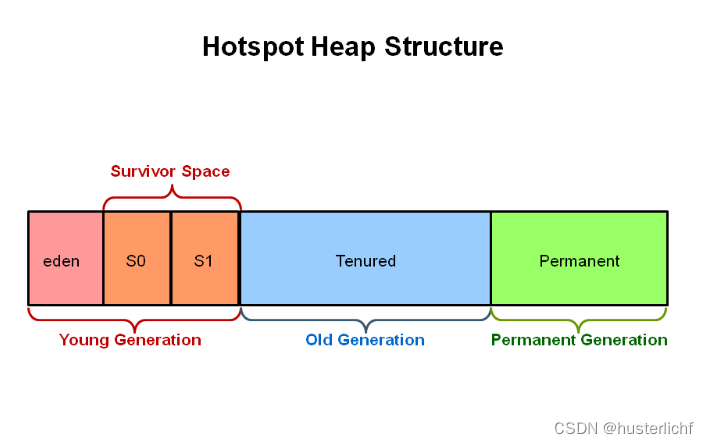
JVM----GC(垃圾回收)详解
一、Automatic Garbage Collection(垃圾回收)简介 Automatic Garbage Collection (自动垃圾回收)是JVM的一个特性,JVM会启动相关的线程,该线程会轮训检查heap memeory,并确定哪些是未被引用的(…...

数据库的三个范式
数据库的三个范式是关系数据库设计中的一组规范,用于确保数据的有效性和一致性。这三个范式分别是: 第一范式(1NF):要求数据库表中的每一列都是不可分割的原子值。换句话说,每个表中的每个字段不能包含多个…...
谷歌浏览器打开白屏 后台还有还有很多google chrome进程在运行
环境: Win10 专业版 谷歌浏览器 版本 116.0.5845.141(正式版本) (64 位) L盾加密终端 问题描述: 谷歌浏览器打开白屏 后台还有还有很多google chrome进程在运行,要全部结束谷歌浏览器进程&…...
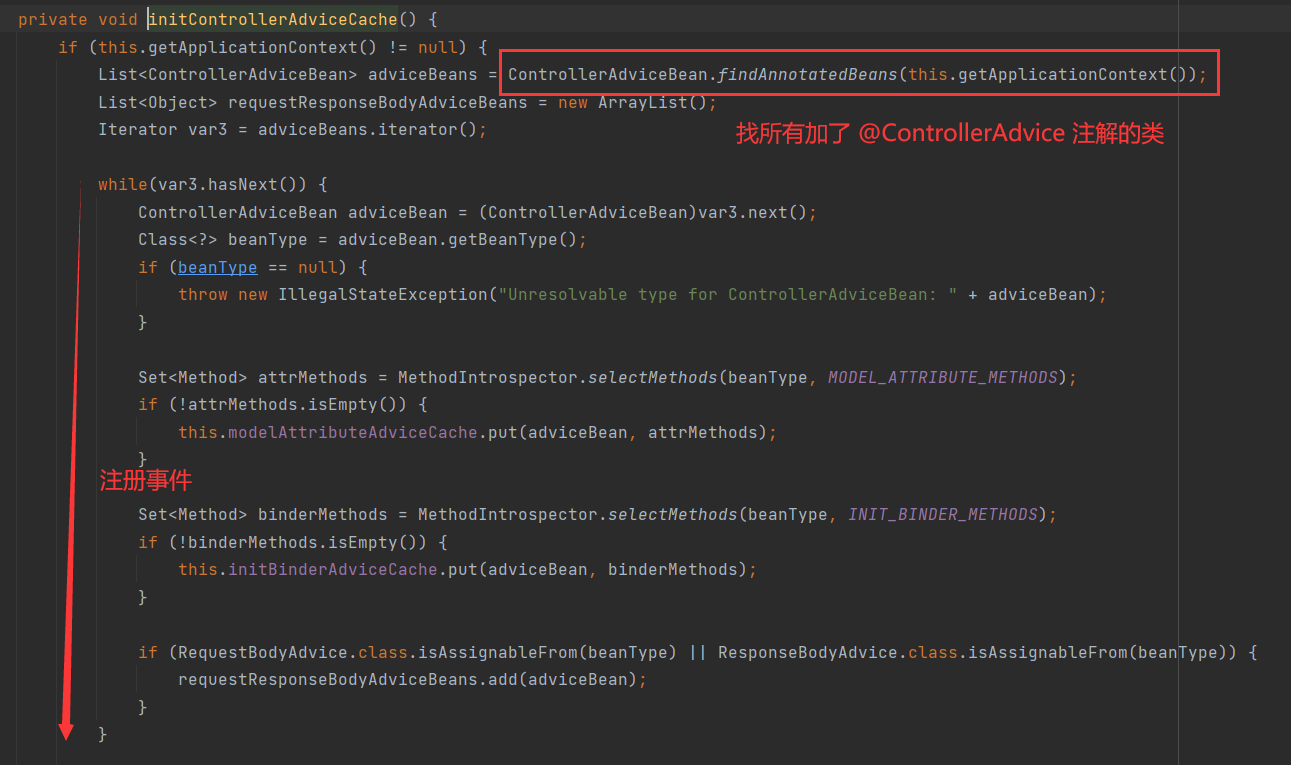
Java EE 突击 15 - Spring Boot 统一功能处理
Spring Boot 统一功能处理 一 . 统一功能的处理1.1 初级阶段 : 不断重复1.2 中级阶段 : 集成方法1.3 高级阶段 : Spring AOP1.4 超高级阶段 : Spring 拦截器准备工作实现拦截器自定义拦截器将自定义拦截器加入到系统配置 拦截器实现原理扩展 : 统一访问前缀添加 二 . 统一异常的…...
JasperReport定义变量后打印PDF变量为null以及整个pdf文件为空白
问题1: JasperReport打印出来的整个pdf文件为空白文件; 问题2:JasperReport定义变量后打印PDF变量为null; 问题1原因是因为缺少数据源JRDataSource JasperFillManager.fillReport(jasperReport, params,new JREmptyDataSource());如果你打印…...

Python 及 Pycharm 的安装 2023.8
Python 及 PyCharm 的安装 仅适用于 Windows 系统! 视频教程:【Python及Pycharm的安装 2023.8】 https://www.bilibili.com/video/BV1A34y1T7Gu 文章目录 Python 及 PyCharm 的安装安装 Python安装 PyCharmHi, PyCharmPyCharm 汉化 安装 Python 进入 …...

java中的线程中断
java中的线程中断 1、线程中断 即 线程的取消/关闭的机制2、线程对中断interrupt()的反应2.1、RUNNABLE:线程在运行或具备运行条件只是在等待操作系统调度2.2、WAITING/TIMED_WAITING:线程在等待某个条件或超时2.3、BLOCKED:线程在等待锁&…...
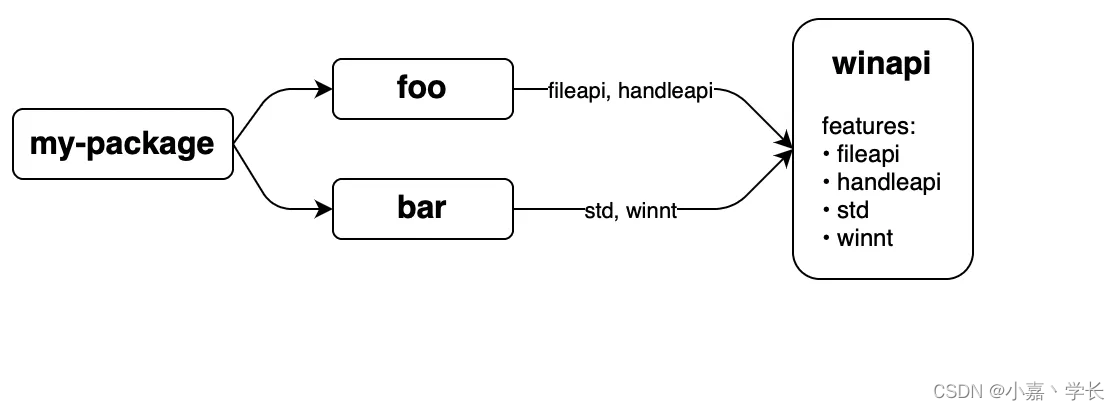
【跟小嘉学 Rust 编程】二十三、Cargo 使用指南
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...
)
R Removing package报错(as ‘lib’ is unspecified)
remove.packages(ggpubr) Removing package from ‘/Library/Frameworks/R.framework/Versions/4.0/Resources/library’ (as ‘lib’ is unspecified) 解决办法: > .libPaths() [1] "/Library/Frameworks/R.framework/Versions/4.0/Resources/library&qu…...
金融信创,软件规划需关注自主安全及生态建设
软件信创化,就是信息技术软件应用创新发展的意思(简称为“信创”)。 相信在中国,企业对于“信创化”这个概念并不陌生。「国强则民强」,今年来中国经济的快速发展,受到了各大欧美强国的“卡脖子”操作的影…...

无重叠区间【贪心算法】
无重叠区间 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。 class Solution {public int eraseOverlapIntervals(int[][] intervals) {//先排序,按照左边界升序,注…...
nlp系列(7)实体识别(Bert)pytorch
模型介绍 本项目是使用Bert模型来进行文本的实体识别。 Bert模型介绍可以查看这篇文章:nlp系列(2)文本分类(Bert)pytorch_bert文本分类_牧子川的博客-CSDN博客 模型结构 Bert模型的模型结构: 数据介绍 …...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
