【数据结构】——树和二叉树的概念
目录
1.树概念及结构
1.1树的概念
1.2 树的相关性质
1.3 树的表示
1.4 树在实际中的运用(表示文件系统的目录树结构)
2.二叉树概念及结构
2.1二叉树概念
2.2 特殊的二叉树
2.3 二叉树的性质
1.树概念及结构
1.1树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
有一个特殊的结点,称为根结点,根节点没有前驱结点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继 因此,树是递归定义的。

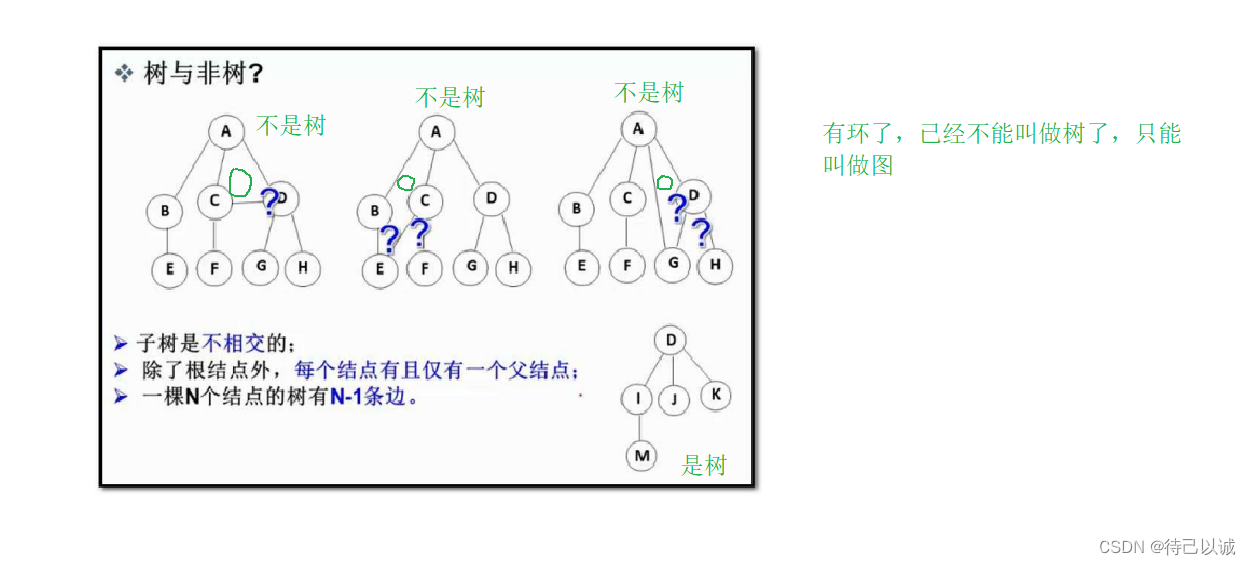
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关性质
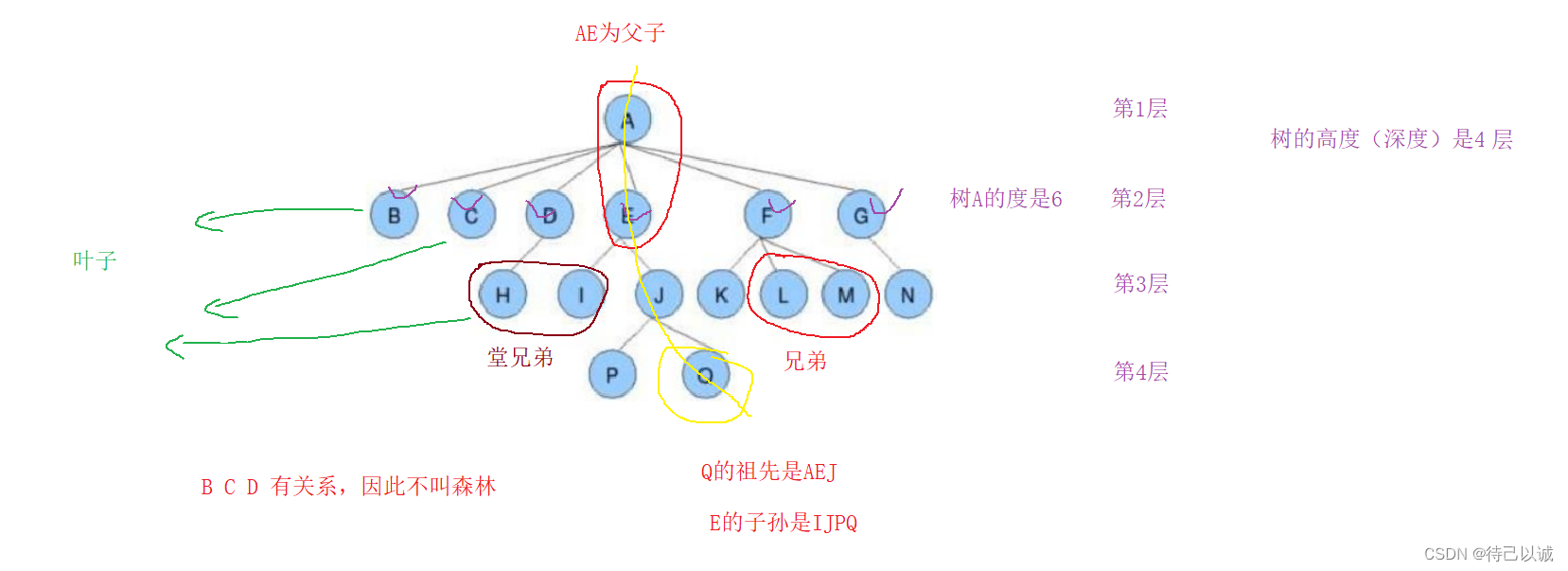
节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点(叶子):度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点(亲兄弟):具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既要保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们这里就简单的了解其中最常用的孩子兄弟表示法(最合适的树结构)。
//孩子兄弟表示法struct TreeNode
{int data;struct TreeNode * child;struct TreeNode * brother;
}
1.4 树在实际中的运用(表示文件系统的目录树结构)

2.二叉树概念及结构
2.1二叉树概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
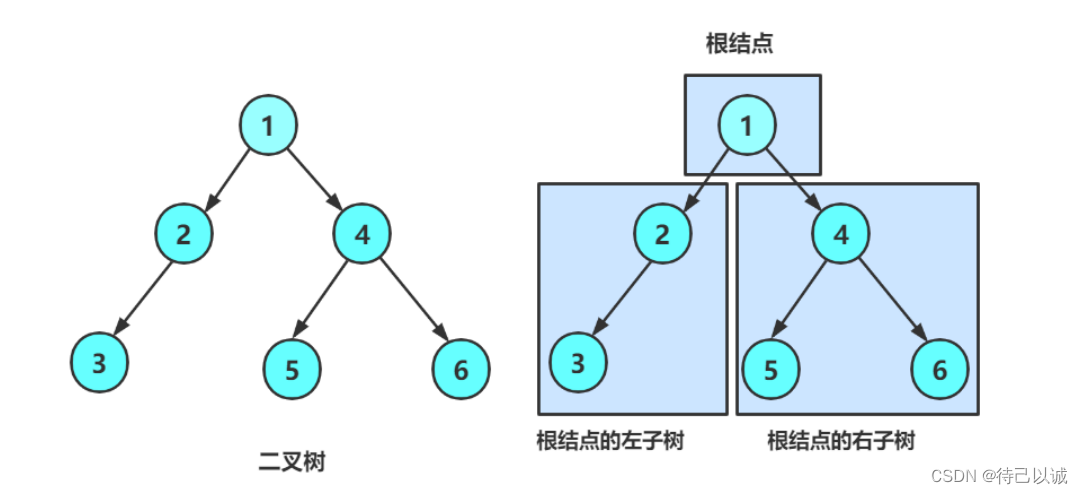
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
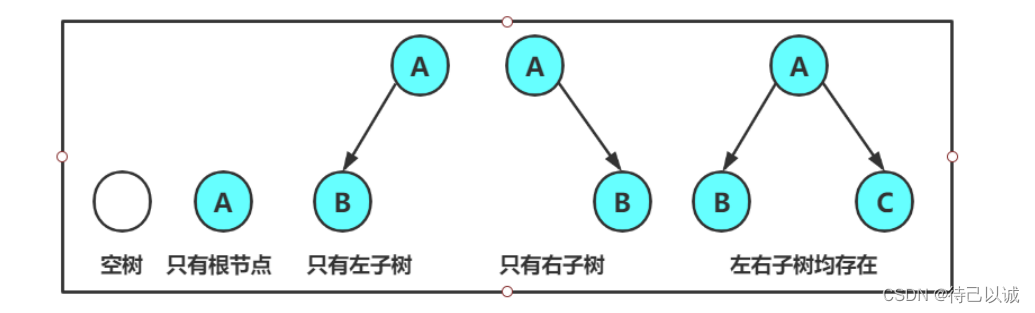
对于任意的二叉树都是由以下几种情况复合而成的:
2.2 特殊的二叉树
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
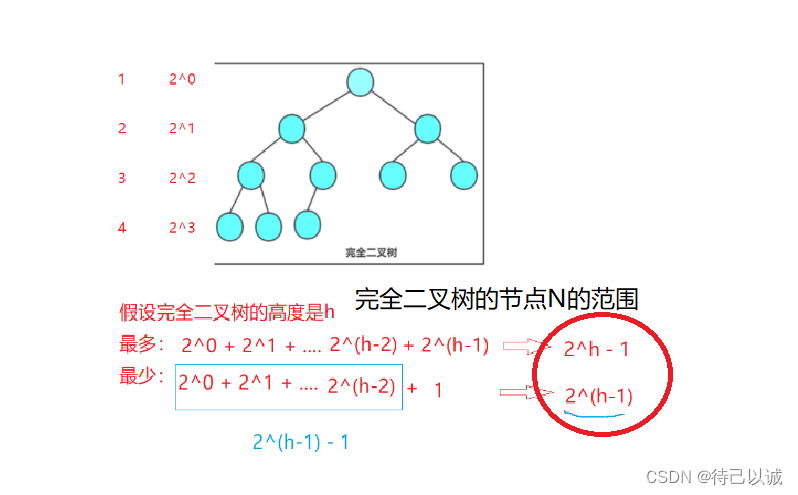
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
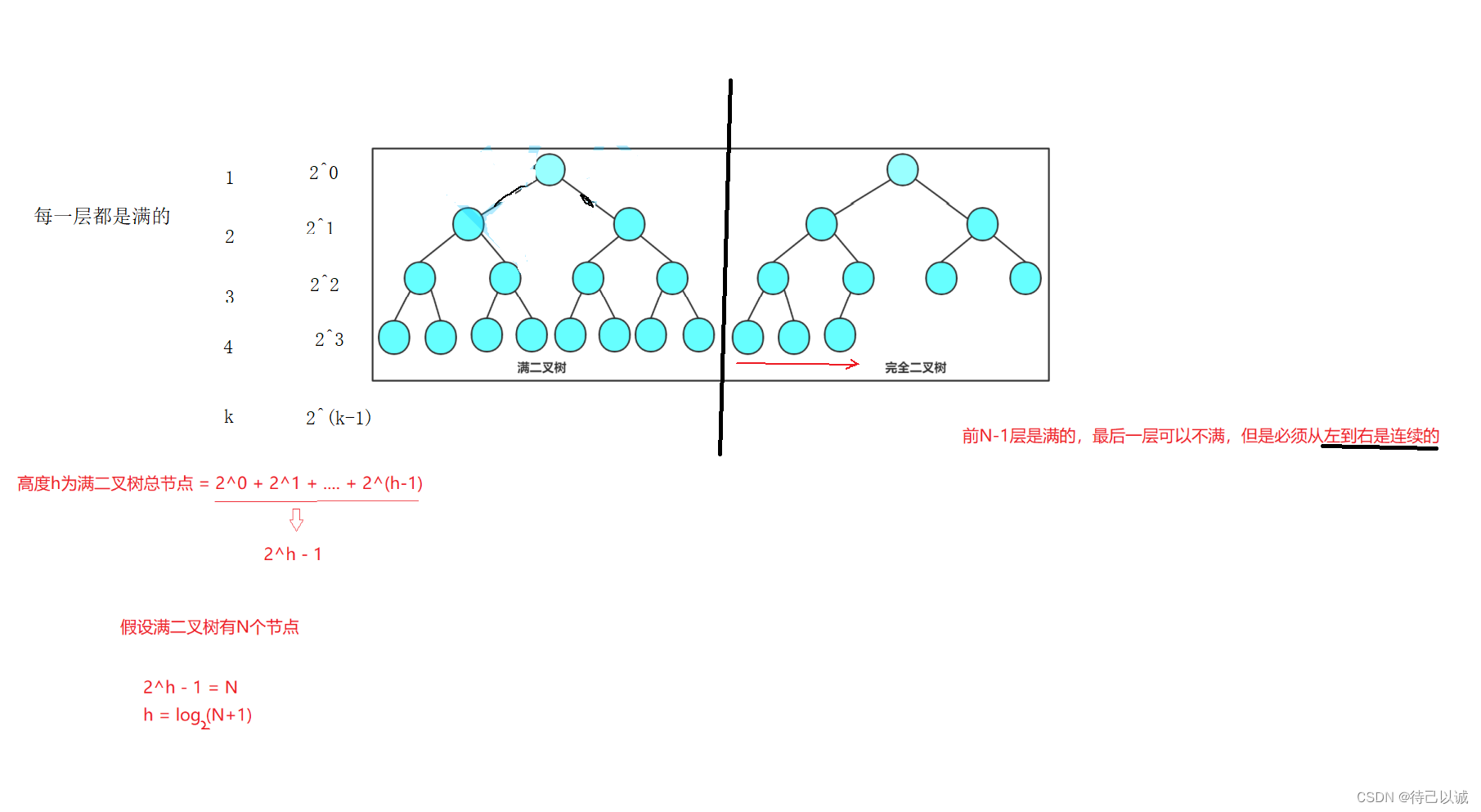
PS:完全二叉树节点的取值范围:
2.3 二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点.(第i层满了)
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1.(满二叉树)
3. 对任何一棵二叉树(非空), 如果度为0其叶结点个数为n0 , 度为2的分支结点个数为n2 ,
则有 n0=n2+1 (度为0的节点总是比度为2的节点多1)
完全二叉树的度为1的节点要么是1个要么是0个。

5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
1. 若i>0,i位置节点的双亲序号:(i-1)/2;若i=0,i为根节点编号,无双亲节点
2. 若2i+1<n,左孩子序号:2i+1,若2i+1>=n,则无左孩子
3. 若2i+2<n,右孩子序号:2i+2,若2i+2>=n,则无右孩子
相关文章:

【数据结构】——树和二叉树的概念
目录 1.树概念及结构 1.1树的概念 1.2 树的相关性质 1.3 树的表示 1.4 树在实际中的运用(表示文件系统的目录树结构) 2.二叉树概念及结构 2.1二叉树概念 2.2 特殊的二叉树 2.3 二叉树的性质 1.树概念及结构 1.1树的概念 树是一种非线性的数据结构…...

Meta分析在生态环境领域里的应用
Meta分析(Meta Analysis)是当今比较流行的综合具有同一主题的多个独立研究的统计学方法,是较高一级逻辑形式上的定量文献综述。20世纪90年代后,Meta分析被引入生态环境领域的研究,并得到高度的重视和长足的发展&#x…...
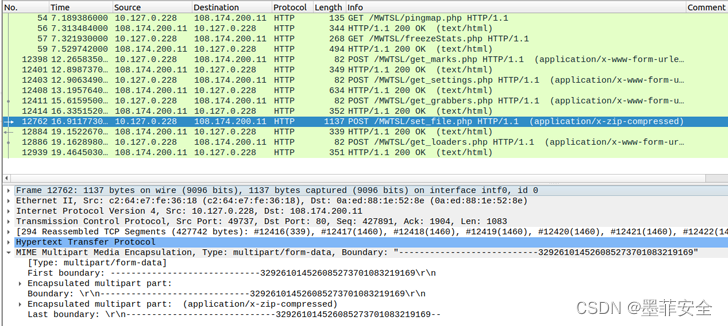
PrivateLoader PPI服务发现RisePro恶意软件窃取分发信息
称为PrivateLoader的按安装付费(PPI)软件下载器服务正用于恶意软件RisePro的信息窃取。Flashpoint 于 2022 年 12月13日发现了新的窃取者,此前发现了在名为Russian Market的非法网络犯罪市场上使用该恶意软件泄露的“几组日志”。RisePro是一…...
)
SQL93 返回购买 prod_id 为 BR01 的产品的所有顾客的电子邮件(一)
描述你想知道订购 BR01 产品的日期,有表OrderItems代表订单商品信息表,prod_id为产品id;Orders表代表订单表有cust_id代表顾客id和订单日期order_date;Customers表含有cust_email 顾客邮件和cust_id顾客idOrderItems表prod_idorde…...
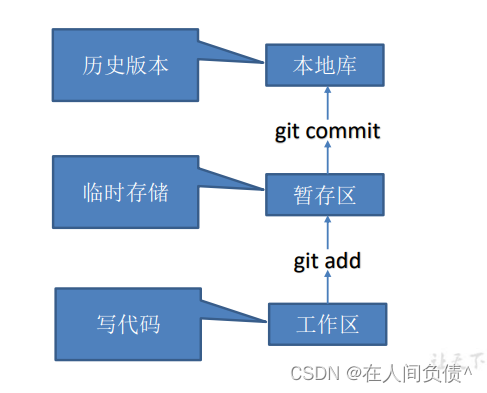
Git ---- 概述
Git ---- 概述1. 何为版本控制2. 为什么需要版本控制3. 版本控制的工具集中式版本控制工具分布式版本控制工具4. Git 简史5. Git 工作机制6. Git 和代码托管中心Git 是一个免费的、开源的分布式版本控制系统,可以快速高效地处理从小型到大型的各种项目。 Git 易于学…...
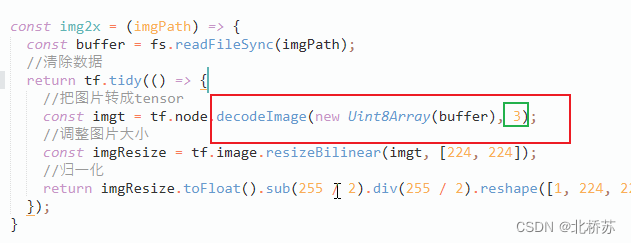
用 tensorflow.js 做了一个动漫分类的功能(二)
前言:前面已经通过采集拿到了图片,并且也手动对图片做了标注。接下来就要通过 Tensorflow.js 基于 mobileNet 训练模型,最后就可以实现在采集中对图片进行自动分类了。这种功能在应用场景里就比较多了,比如图标素材站点࿰…...
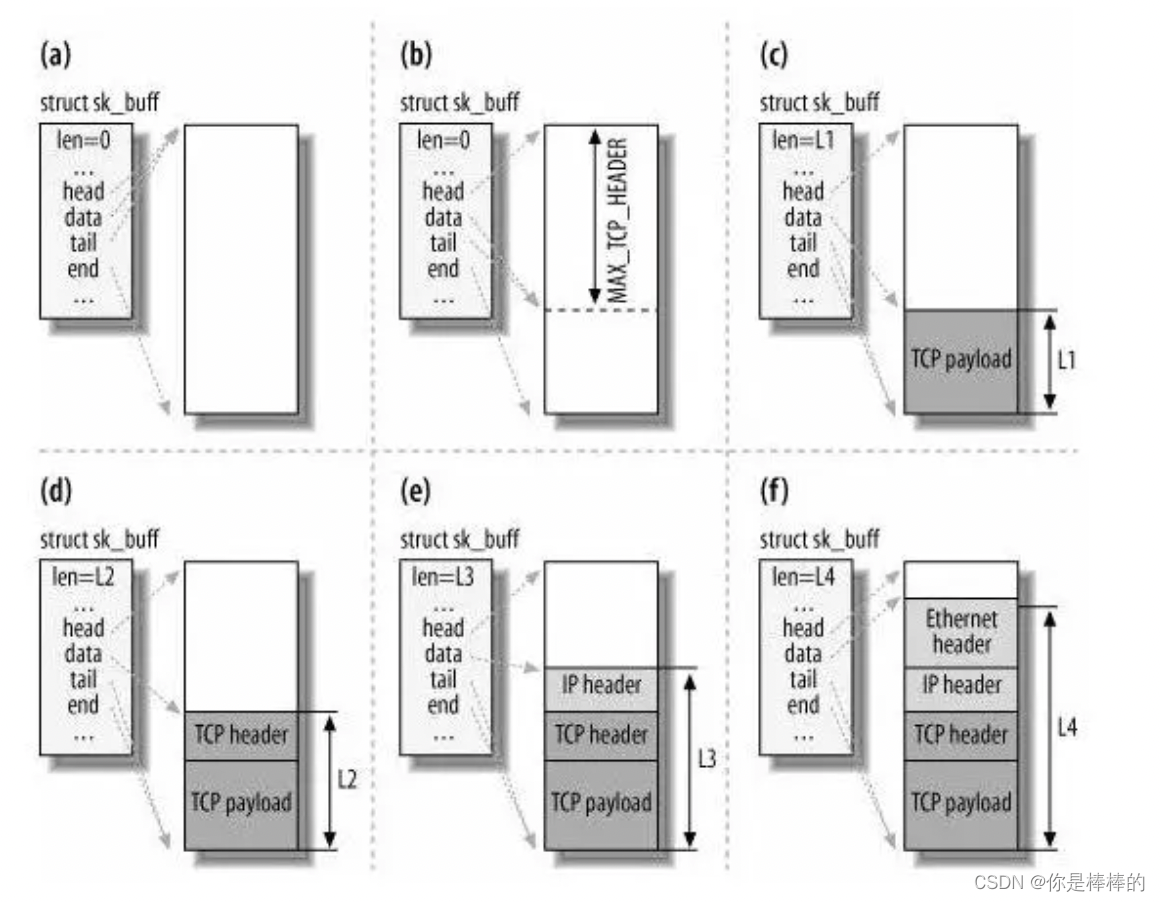
小林coding
一、图解网络 问大家,为什么要有TCP/Ip网络模型? 对于同一台设备上的进程通信,有很多种方式,比如有管道、消息队列、共享内存、信号等方式,对于不同设备上的进程通信,就需要有网络通信,而设备是…...

操作系统真相还原_第6章:完善内核
文章目录6.1 函数调用约定简介6.2 汇编语言和C语言混合编程汇编调用CC调用汇编6.3 实现打印函数流程程序编译并写入硬盘执行6.4 内联汇编简介汇编语言AT&T语法基本内联汇编扩展内联汇编6.1 函数调用约定简介 调用约定: calling conventions 调用函数时的一套约…...
SmoothNLP新词发现算法的改进实现
SmoothNLP新词发现算法的改进实现 背景介绍 新词发现也叫未登录词提取,依据 《统计自然语言处理》(宗成庆),中文分词有98%的错误来自"未登录词"。即便早就火遍大江南北的Bert也不能解决"未登录词"的Encoding问题,便索性…...

实时渲染为什么快,能不能局域网部署点量云
提到渲染很多有相关从业经验的人员可能会想起,自己曾经在电脑上渲染一个模型半天或者更长的 时间才能完成的经历。尤其是在项目比较着急的时候,这种煎熬更是难受。但现在随着实时渲染和云渲染行业的发展,通过很多方式可以提升渲染的时间和效率…...

网络游戏该如何防护ddos/cc攻击
现在做网络游戏的企业都知道服务器的安全对于我们来说很重要!互联网上面的 DDoS 攻击和 CC 攻击等等无处不在,而游戏服务器对服务器的防御能力和处理能力要求更高,普通的服务器则是比较注重各方面能力的均衡。随着游戏行业的壮大,…...

项目管理体系1-4练习题1-10答案
题目1 每周一次的项目会议上,一位团队成员表示在修订一项可交付成果时,一名销售经理对客户服务过程想出一项变更讨论,影响到整个项目,项目经理对销售参与到项目可交付成果感到吃惊,经理事先应该怎么做去阻止这些情况&…...

sHMIctrl智能屏幕使用记录
手上有个案子,“按压机器人”,功能是恒定一个力按下一定时间。 屏幕选型使用“sHMIctrl”,一下记录使用过程中遇到的问题以及解决方法。 目录 问题1:按键控件做定时触发,模拟运行时触发不了。 问题2:厂家…...
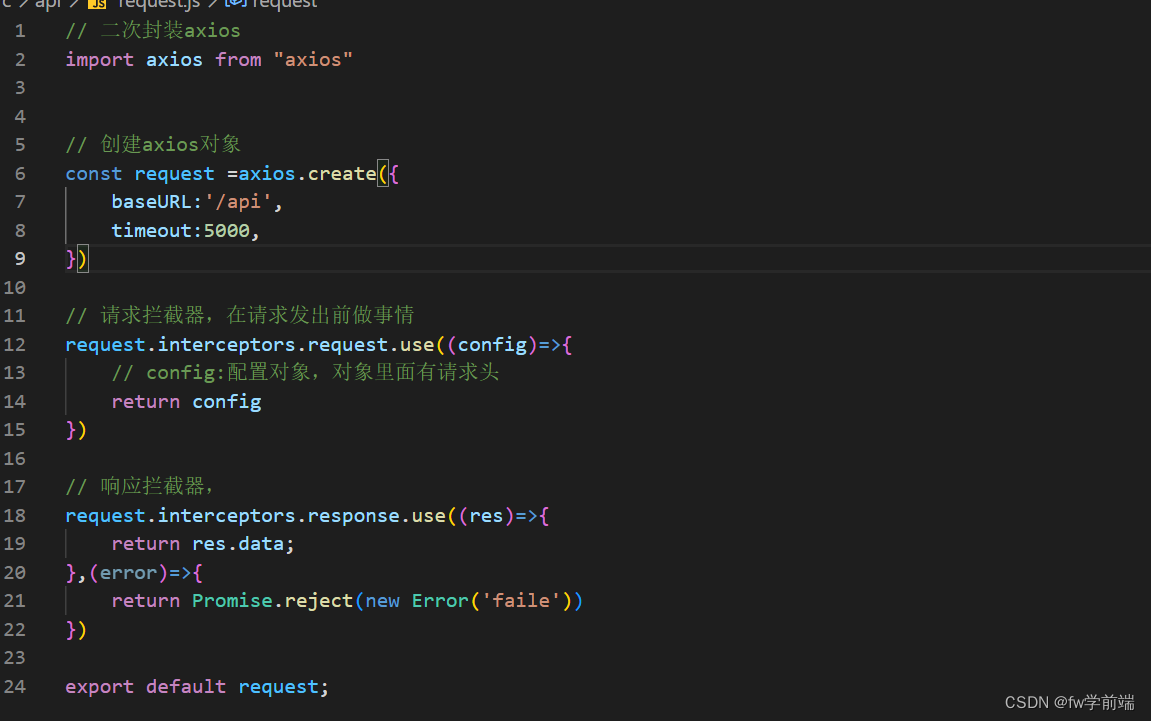
2.20 crm day01 配置路由router less使用 axios二次封装
需求: 目录 1.配置路由 2.less使用 vue2使用以下版本 3.axios二次封装 1.配置路由 1.1.1 官方链接:安装 | Vue Router npm i vue-router3.6.5 注意:vue2项目不能用vue-router四版本以上 1.2.1.创建router/index.js 在该文件中 //1.引…...
【LeetCode】剑指 Offer 10- I. 斐波那契数列 p74 -- Java Version
题目链接: 1. 题目介绍() 写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下: F(0) 0, F(1) 1F(N) F(N - 1) F…...
论文笔记:DropMessage: Unifying Random Dropping for Graph Neural Networks
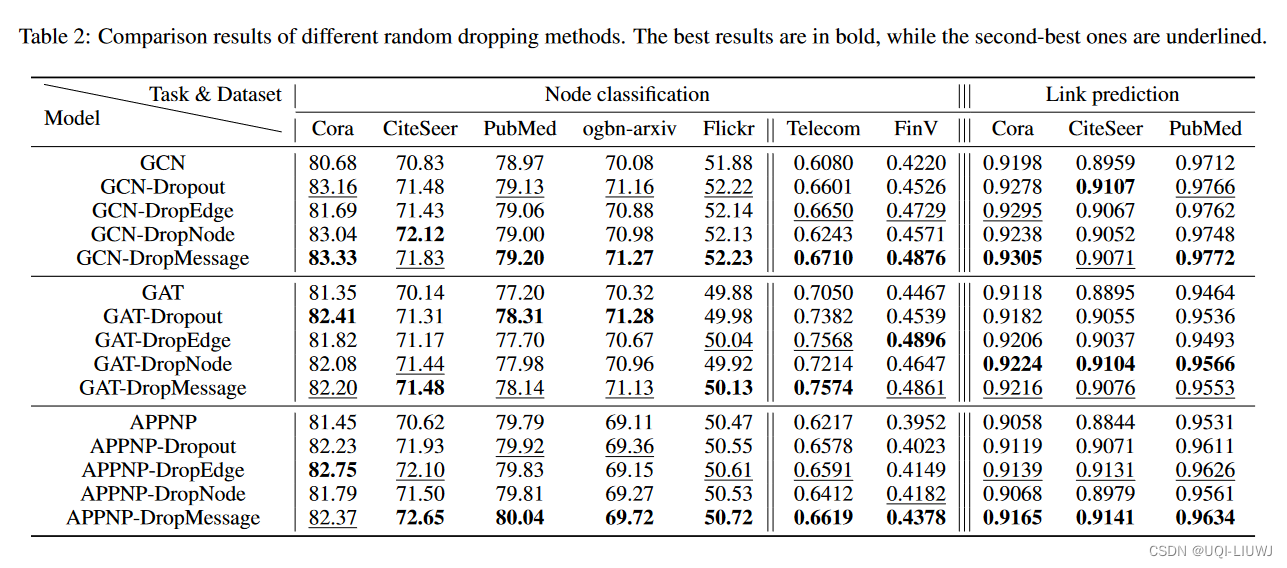
(AAAI 23 优秀论文) 1 intro GNN的一个普遍思路是,每一层卷积层中,从邻居处聚合信息 尽管GNN有显著的进步,但是在大规模图中训练GNN会遇到各种问题: 过拟合 过拟合之后,GNN的泛化能力就被限制…...
木鱼cms系统审计小结
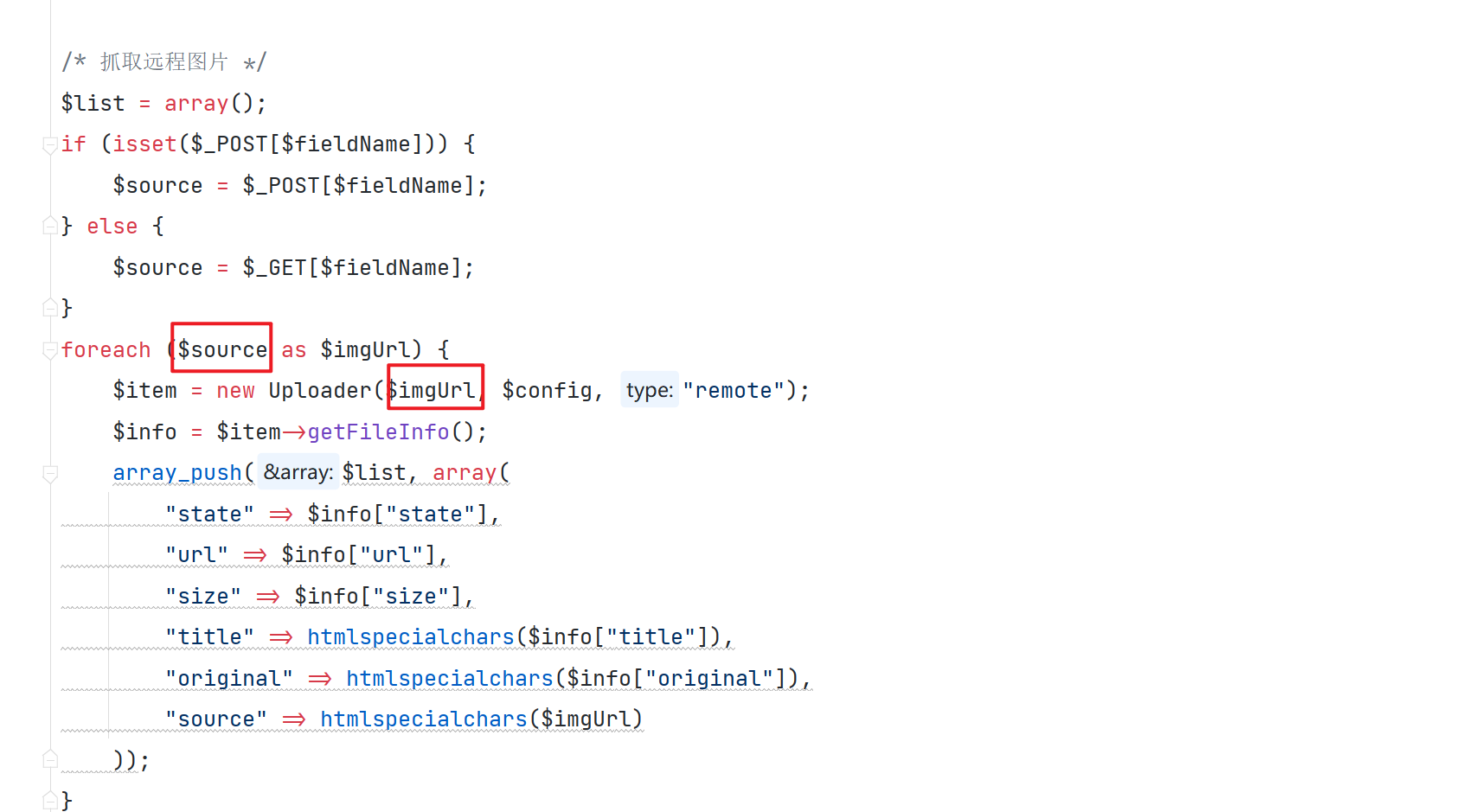
MuYuCMS基于Thinkphp开发的一套轻量级开源内容管理系统,专注为公司企业、个人站长提供快速建站提供解决方案。 环境搭建 我们利用 phpstudy 来搭建环境,选择 Apache2.4.39 MySQL5.7.26 php5.6.9 ,同时利用 PhpStorm 来实现对项目的调试 …...

软件测试面试-一线大厂必问的测试思维面试题
五、测试思维5.1 打电话功能怎么去测?我们会从几个方面去测试:界面、功能、兼容性、易用性、安全、性能、异常。1)界面我们会测试下是否跟界面原型图一致,考虑浏览器不同显示比例,屏幕分辨率。2)功能&#…...
企业级分布式应用服务 EDAS
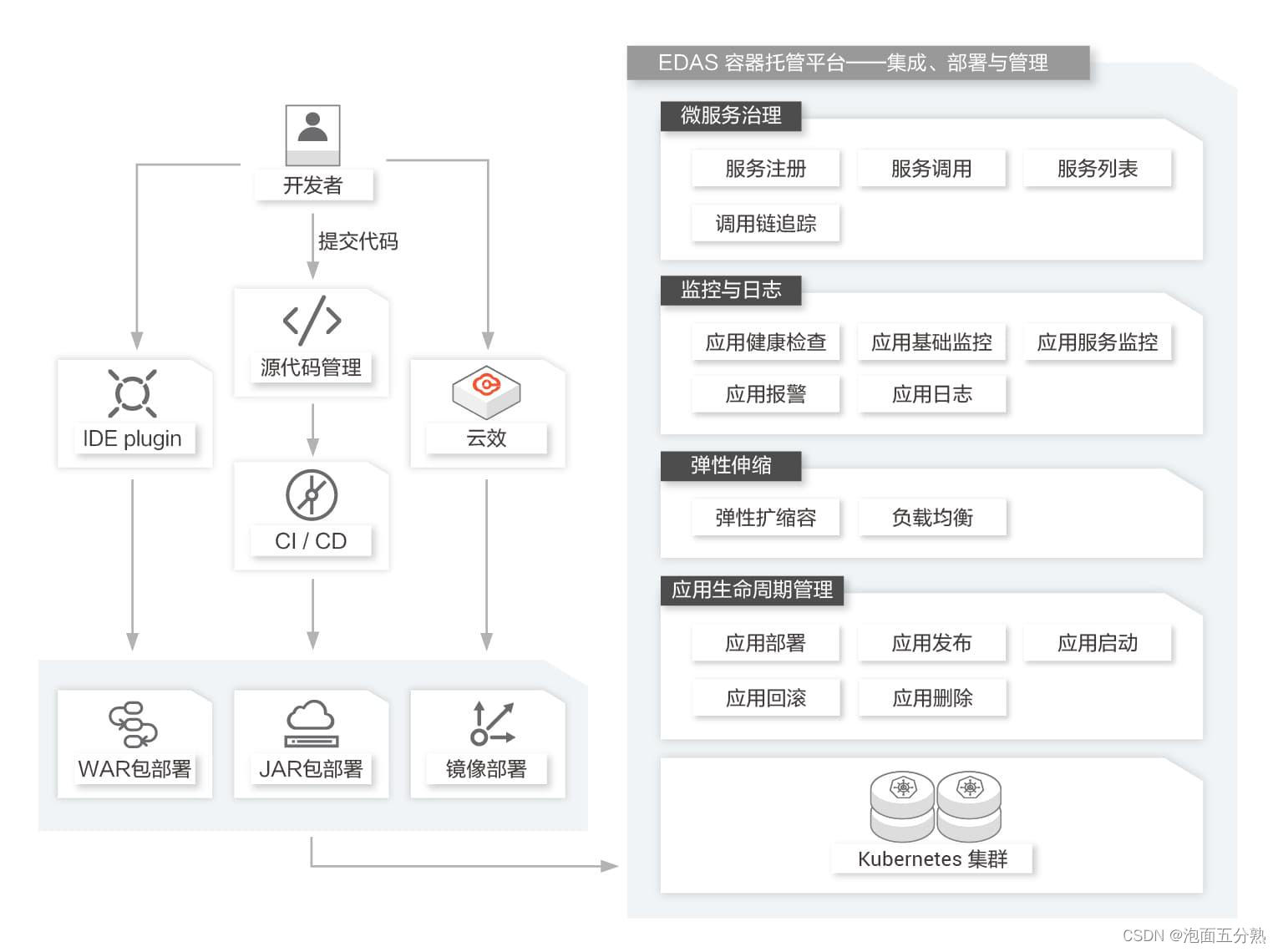
什么是企业级分布式应用服务EDAS企业级分布式应用服务EDAS(Enterprise Distributed Application Service)是一个应用托管和微服务管理的云原生PaaS平台,提供应用开发、部署、监控、运维等全栈式解决方案,同时支持Spring Cloud和Ap…...
弄懂 Websocket 你得知道的这 3 点
1. WebSocket原理 WebSocket同HTTP一样也是应用层的协议,但是它是一种双向通信协议,是建立在TCP之上的。 WebSocket是一种在单个TCP连接上进行全双工通信的协议。WebSocket API也被W3C定为标准。 WebSocket使得客户端和服务器之间的数据交换变得更加简…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...