机器人中的数值优化(八)——拟牛顿方法(上)
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
十、拟牛顿方法
1、拟牛顿方法介绍
Newton方法的缺点是在每步迭代时需计算Hesse矩阵 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk),为此要计算n(n + 1)/2个二阶偏导数;若该方法产生的迭代点不能充分接近极小点, ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)的正定性不能保证。Newton方法的优点在于它具有二阶收敛的速度.这促使我们去考虑是否可以构造一种方法,它既不需要计算二阶偏导数,又具有较快的收敛速度。

假设我们要构造一个矩阵M去近似Hessian矩阵,那么M应该满足什么条件?
①:它应该不需要计算所有元素的二阶导
②:可以不用显式的求解线性方程组,方程组应该有闭式解,以便很快的解出
③:它应该不需要是满秩的,所以它的存储应该是紧凑的
④:它必须保持下降方向,即它必须是正定的
⑤:它应该包含曲率信息(局部二次近似),即应该逼近Hessian矩阵

–
从下图的推导可以看出,当近似矩阵M是正定的矩阵时,可以保证搜索方向与负梯度方向成锐角,即可保证搜索方向为下降方向。

☆☆☆注:在深蓝学院课程机器人中的数值优化中,用H表示Hessian矩阵,用M表示Hessian矩阵的近似,用B表示M的逆矩阵,而在数值最优化方法(高立 编著)这本书中,用B表示Hessian矩阵的近似,而用H表示B的逆矩阵,在下文的文字描述中采用数值最优化方法(高立 编著)这本书中的表示方法,下文中的图片大部分是基于深蓝学院课程机器人中的数值优化课程中的PPT进行修改补充后而形成的,采用该课程的表示方法
假定当前迭代点为 x k + 1 x_{k+1} xk+1,若我们用已得到的 x k x_{k} xk, x k + 1 x_{k+1} xk+1及其一阶导数信息 ∇ f ( x k ) \nabla f\left(x_{k}\right) ∇f(xk)和 ∇ f ( x k + 1 ) \nabla f\left(x_{k+1}\right) ∇f(xk+1),构造一个正定矩阵 B k + 1 B_{k+1} Bk+1作为 ∇ f 2 ( x k + 1 ) \nabla f^2\left(x_{k+1}\right) ∇f2(xk+1)的近似,这样下降方向 d k + 1 d_{k+1} dk+1 由以下方程组给出
B k + 1 d = − ∇ f ( x k + 1 ) {B}_{k+1}d=-\nabla f\left(x_{k+1}\right) Bk+1d=−∇f(xk+1)
然而这样做仍需求解一个线性方程组.进一步的改进为用相同的信息构造一个矩阵 H k + 1 H_{k+1} Hk+1作为 ∇ f 2 ( x k + 1 ) − 1 \nabla f^2\left(x_{k+1}\right)^{-1} ∇f2(xk+1)−1的近似,这样下降方向 d k + 1 d_{k+1} dk+1就可以由下式给出
d = − H k + 1 ∇ f ( x k + 1 ) d=-H_{k+1}\nabla f\left(x_{k+1}\right) d=−Hk+1∇f(xk+1)
近似矩阵的构造应该是简单有效的,它应具有如下的条件:
①:只需 f ( x ) f(x) f(x)的一阶导数信息;
②: B k + 1 {B}_{k+1} Bk+1 ( H k + 1 ) (H_{k+1}) (Hk+1)正定,以保证方向的下降性;
③:方法具有较快的收敛速度。
对梯度进行泰勒展开,去掉高阶小量,可得下式
∇ f ( x k + 1 ) − ∇ f ( x k ) ≈ ∇ 2 f ( x ) ∗ ( x k + 1 − x k ) \nabla f\left(x_{k+1}\right)-\nabla f\left(x_{k}\right) ≈ \nabla^2 f(x)*(x_{k+1}-x_k) ∇f(xk+1)−∇f(xk)≈∇2f(x)∗(xk+1−xk)
若进行以下定义:
s k = x k + 1 − x k , y k = ∇ f ( x k + 1 ) − ∇ f ( x k ) , \begin{array}{c}s_k=x_{k+1}-x_k,\\ \\ y_k=\nabla f\left(x_{k+1}\right)-\nabla f\left(x_{k}\right),\end{array} sk=xk+1−xk,yk=∇f(xk+1)−∇f(xk),
则 B k + 1 {B}_{k+1} Bk+1作为 ∇ f 2 ( x k + 1 ) \nabla f^2\left(x_{k+1}\right) ∇f2(xk+1)的近似,应该满足以下方程:
B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1sk=yk
该方程称为拟Newton方程或拟Newton条件。若记 H k + 1 = B k + 1 − 1 , H_{k+1}=B_{k+1}^{-1}, Hk+1=Bk+1−1,则 H k + 1 H_{k+1} Hk+1应该满足下式
H k + 1 y k = s k . H_{k+1}y_k=s_k. Hk+1yk=sk.
拟Newton方法是指由 B k + 1 d = − ∇ f ( x k + 1 ) {B}_{k+1}d=-\nabla f\left(x_{k+1}\right) Bk+1d=−∇f(xk+1)式或者 d = − H k + 1 ∇ f ( x k + 1 ) d=-H_{k+1}\nabla f\left(x_{k+1}\right) d=−Hk+1∇f(xk+1)式确定迭代方向d的最优化方法,其中的 B k + 1 {B}_{k+1} Bk+1需满足拟 Newton条件 B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1sk=yk, H k + 1 {H}_{k+1} Hk+1需满足拟Newton条件 H k + 1 y k = s k H_{k+1}y_k=s_k Hk+1yk=sk.
下面我们给出一般拟Newton方法的结构,其算法以矩阵 H k + 1 H_{k+1} Hk+1的迭代为例.

在上述算法中,初始矩阵H通常取为单位矩阵,这样算法的第一步迭代的迭代方向取为负梯度方向.
那么如何修正 H k {H}_{k} Hk得 H k + 1 {H}_{k+1} Hk+1呢?,即如何确定在下式中的 Δ H k \Delta H_k ΔHk呢?
H k + 1 = H k + Δ H k H_{k+1}=H_k+\Delta H_k Hk+1=Hk+ΔHk
Δ H k \Delta H_k ΔHk的取法是多种多样的,但它应具有简单、计算量小、有效的特点.下面介绍几种重要的修正 H k H_k Hk与 B k B_k Bk的公式.
1、拟牛顿方法修正公式
(1)对称秩1公式(SR1)
对称秩1(Symmetric Rank 1,SR1)公式是由Broyden、Davidon等人独立提出的。
H k + 1 S R 1 = H k + ( s k − H k y k ) ( s k − H k y k ) T ( s k − H k y k ) T y k , H_{k+1}^{\mathrm{SR1}}=H_k+\dfrac{(s_k-H_ky_k)(s_k-H_ky_k)^{\mathrm{T}}}{(s_k-H_ky_k)^{\mathrm{T}}y_k}, Hk+1SR1=Hk+(sk−Hkyk)Tyk(sk−Hkyk)(sk−Hkyk)T,
B k + 1 S R 1 = B k + ( y k − B k s k ) ( y k − B k s k ) T ( y k − B k s k ) T s k . B_{k+1}^{\mathrm{SR1}}=B_k+\dfrac{(y_k-B_k s_k)(y_k-B_k s_k)^{\mathrm{T}}}{(y_k-B_k s_k)^{\mathrm{T}}s_k}. Bk+1SR1=Bk+(yk−Bksk)Tsk(yk−Bksk)(yk−Bksk)T.
(2)DFP公式
DFP公式,或者说DFP方法,首先是由Davidon于1959年提出,后经Fletcher 和 Powell发展得到的。该方法是第一个被提出的拟 Newton方法,它为拟 Newton方法的建立与发展奠定了基础.
H k + 1 D F P = H k + s k s k T s k T y k − H k y k y k T H k y k T H k y k . H_{k+1}^{\mathrm{DFP}}=H_k+\frac{s_k s_k^{\mathrm{T}}}{s_k^{\mathrm{T}}y_k}-\frac{H_ky_ky_k^{\mathrm{T}}H_k}{y_k^{\mathrm{T}}H_ky_k}. Hk+1DFP=Hk+skTykskskT−ykTHkykHkykykTHk.
我们称采用DFP公式来修正矩阵的拟Newton方法为DFP方法。假定 H k H_k Hk与 H k + 1 H_{k+1} Hk+1都可逆,根据Shermann-Morrison-Woodbury 公式,由上式可以导出 B k + 1 B_{k+1} Bk+1的修正公式
B k + 1 D F P = B k + ( 1 + s k T B k s k s k T y k ) y k y k T s k T y k − ( y k s k T B k + B k s k y k T s k T y k ) . B_{k+1}^{\mathrm{DFP}}=B_{k}+\left(1+\frac{s_{k}^{\mathrm{T}}B_{k}s_{k}}{s_{k}^{\mathrm{T}}y_{k}}\right)\frac{y_{k}y_{k}^{\mathrm{T}}}{s_{k}^{\mathrm{T}}y_{k}}-\left(\frac{y_{k}s_{k}^{\mathrm{T}}B_{k}+B_{k}s_{k}y_{k}^{\mathrm{T}}}{s_{k}^{\mathrm{T}}y_{k}}\right). Bk+1DFP=Bk+(1+skTykskTBksk)skTykykykT−(skTykykskTBk+BkskykT).
上式其实也是下面问题的解:
min ∥ W − T ( B − B k ) W − 1 ∥ F , s.t. B = B T , B s k = y k , \begin{array}{l}\min\|W^{-\mathrm T}(B-B_k)W^{-1}\|_{\mathrm F},\\ \text{s.t.}\quad B=B^{\mathrm T},B s_k=y_k,\end{array} min∥W−T(B−Bk)W−1∥F,s.t.B=BT,Bsk=yk,
其中 W ∈ R n × n W ∈R^{n×n} W∈Rn×n非奇异。 W T W = B W^TW=B WTW=B满足拟Newton条件 B s k = y k Bs_k=y_k Bsk=yk、这个问题的目的是在所有对称、满足拟Newton条件的矩阵中,寻找在加权F范数意义下与 B k B_k Bk的差最小的矩阵.如果在这个问题中改变目标函数的矩阵范数,就得到其他的拟Newton修正公式
参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化
相关文章:

机器人中的数值优化(八)——拟牛顿方法(上)
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,…...
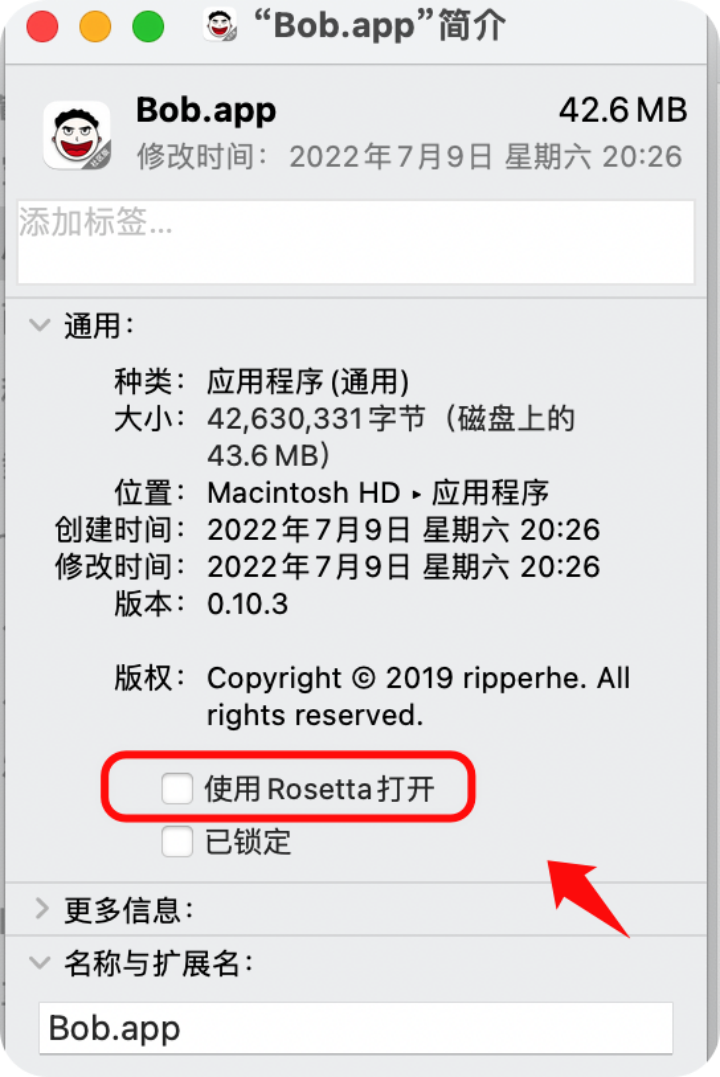
mac安装adobe需要注意的tips(含win+mac all安装包)
M2芯片只能安装2022年以后的(包含2022年的) 1、必须操作的开启“任何来源” “任何来源“设置,这是为了系统安全性,苹果希望所有的软件都从商店或是能验证的官方下载,导致默认不允许从第三方下载应用程序。macOS sie…...

C/C++学习网址
1、http://snippets.dzone.com/tag/c/ --数以千计的有用的C语言源代码片段 2、http://www.hotscripts.com/category/c-cpp/scripts-programs/ Hotscripts --提供数以百计的C和C脚本和程序。所有程序都分为不同的类别。 3、http://www.planetsourcecode.com/vb/default.asp?lng…...

Typora导出的PDF目录标题自动加编号
Typora导出的PDF目录标题自动加编号 在Typora主题文件夹增加如下文件后,标题便自动加上了编号: https://gitcode.net/as604049322/blog_data/-/blob/master/base.user.css 例如: 但是导出的PDF中,目录却没有编号: 这…...
)
【React】React学习:从初级到高级(二)
React学习【二】 2 添加交互2.1 响应事件2.1.1 添加事件处理函数2.1.2 在事件处理函数中读取props2.1.3 将事件处理函数作为props传递2.1.4 命名事件处理函数prop2.1.5 事件传播2.1.6 阻止传播2.1.7 传递处理函数作为事件传播的替代方案2.1.8 阻止默认行为 2.2 State: 组件的记…...

无法将类型为“Newtonsoft.Json.Linq.JObject”的对象转换为类型“Newtonsoft.Json.Linq.JArray”解决方法
对于“Newtonsoft.Json.Linq.JObject”的对象强制类型转换为类型“Newtonsoft.Json.Linq.JArray”报错 第一的图为对象{“*************”:“********”} 第二个图片为数组[{“…”:“…”}] 在我这里进行强制转换对象转换为类型“Newtonsoft.Json.Linq.JArray”报错. 那我们…...
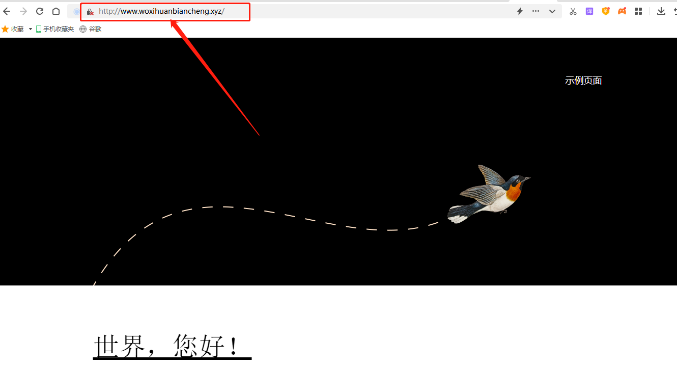
从零开始,无需公网IP,搭建本地电脑上的个人博客网站并发布到公网
文章目录 前言1. 安装套件软件2. 创建网页运行环境 指定网页输出的端口号3. 让WordPress在所需环境中安装并运行 生成网页4. “装修”个人网站5. 将位于本地电脑上的网页发布到公共互联网上 前言 在现代社会,网络已经成为我们生活离不开的必需品,而纷繁…...

Excel VSTO开发6 -Range对象
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 6 Range对象 Excel中最重要的一个对象是Range对象,它可以代表某一单元格、某一行、某一列、某一区域(该区域…...
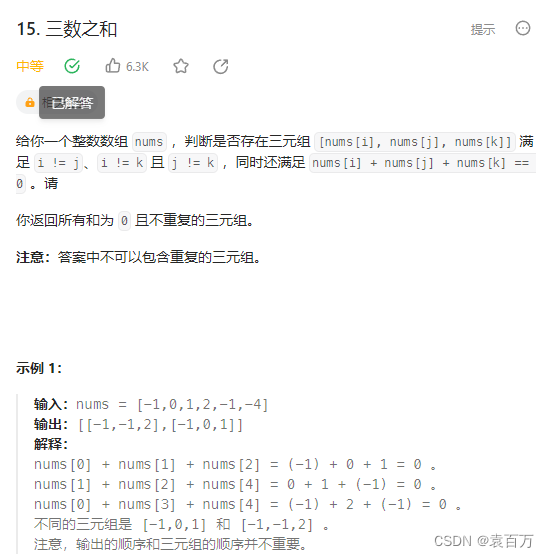
LeetCode 15 三数之和
题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目解析 // 1. 排序双指针 // 2. 固定一个值nums[i] 然后去剩下的位置去找 两数之和符合nums[j]nums[k]是否等于-nums[i] // 3. 细节问题:由于题目中是不可以包含重复的三元组的…...
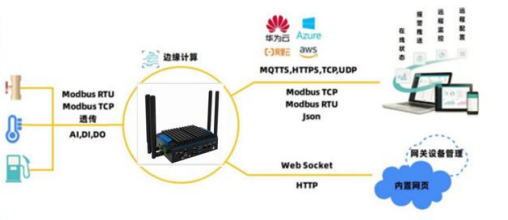
车船边缘网关是如何给车辆船只定位的?
随着智能交通系统的不断发展,车路协同成为了重要的研究方向之一。而AI边缘计算网关在这个领域中发挥着至关重要的作用。本文将重点介绍AI边缘计算网关在车路协同中的应用,并强调其中的重点词汇或短语。 首先,什么是AI边缘计算网关࿱…...
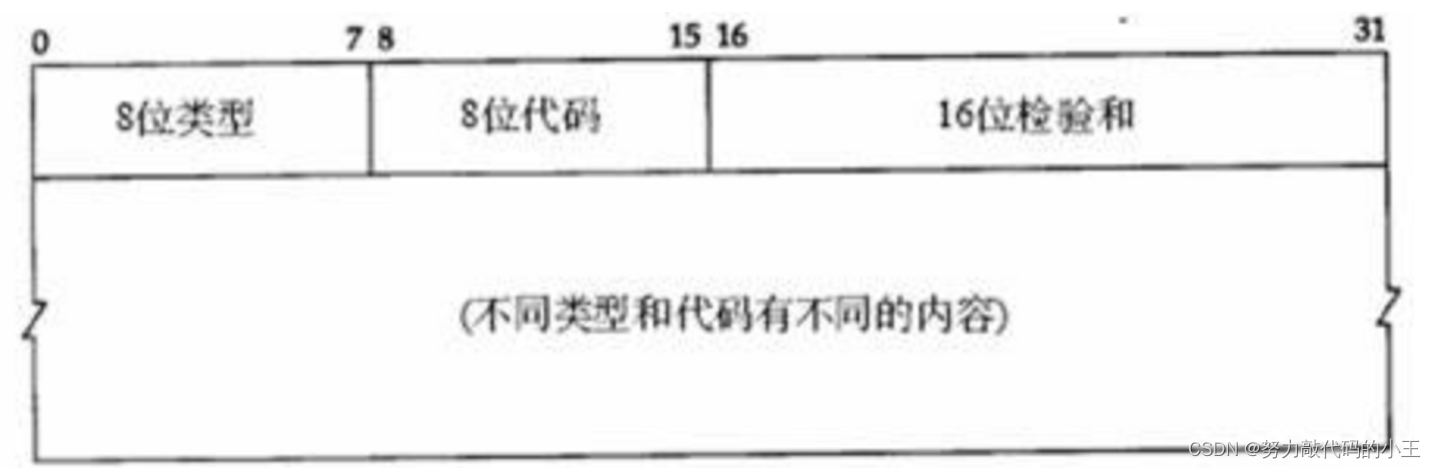
详解MAC帧、ARP、DNS、ICMP协议
局域网通信原理 比如新建了一个内网,如果一台机器A找机器B,封FRAME时(OSI的第二层用的数据格式),要封装对方的MAC,开始时A不知道B的MAC,只知道IP,它就发一个ARP包,源IP是…...

Leetcode:【169. 多数元素】
题目 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 难度:简单 题目链接:169. 多数元素 示例 1ÿ…...

好用免费的Chat GPT
MindLink麦灵 你问我答 灵感 持续更新中。。。。...

MySQL-MHA
目录 1、什么是 MHA 2、MHA 的组成 3、MHA 的特点 3.1 MHA工作原理总结如下 4、搭建 MySQL MHA 4.1 实验环境配置 MHA架构 故障模拟 4.2 安装MHA所有组件 4.3 故障模拟 4.4 总结 1、什么是 MHA MHA(MasterHigh Availability)是一套优秀的My…...
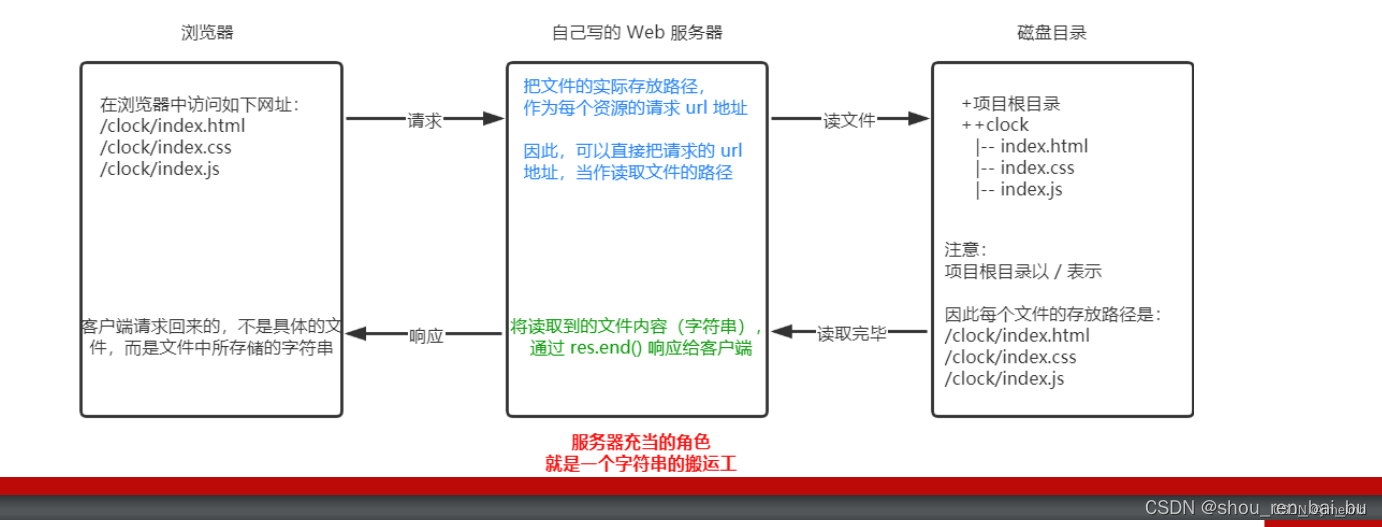
初识Node.js与内置模块
1. 初识 Node.js 1.1 回顾与思考 1. 已经掌握了哪些技术 2. 浏览器中的 JavaScript 的组成部分 3. 思考:为什么 JavaScript 可以在浏览器中被执行 4. 思考:为什么 JavaScript 可以操作 DOM 和 BOM 5. 浏览器中的 JavaScript 运行环境 6. 思考ÿ…...
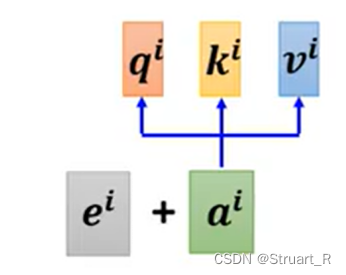
NLP(1)--NLP基础与自注意力机制
目录 一、词向量 1、概述 2、向量表示 二、词向量离散表示 1、one-hot 2、Bag of words 3、TF-IDF表示 4、Bi-gram和N-gram 三、词向量分布式表示 1、Skip-Gram表示 2、CBOW表示 四、RNN 五、Seq2Seq 六、自注意力机制 1、注意力机制和自注意力机制 2、单个输出…...

Ubuntu 升级cuda版本与切换
下载cuda版本 进:CUDA Toolkit 12.2 Downloads | NVIDIA Developer wget https://developer.download.nvidia.com/compute/cuda/12.2.0/local_installers/cuda_12.2.0_535.54.03_linux.runsudo sh ./cuda_12.2.0_535.54.03_linux.run --toolkit --silent --overrid…...

精讲算法的时间复杂度
目录 一、算法效率 1.算法效率 1.1如何衡量一个算法的好坏 1.2算法的复杂度 二、时间复杂度 1.时间复杂度的概念 2.大O的渐进表示法 3.常见时间复杂度的计算举例 三、空间复杂度 一、算法效率 1.算法效率 1.1如何衡量一个算法的好坏 long long Fib(int N) {if(N <…...
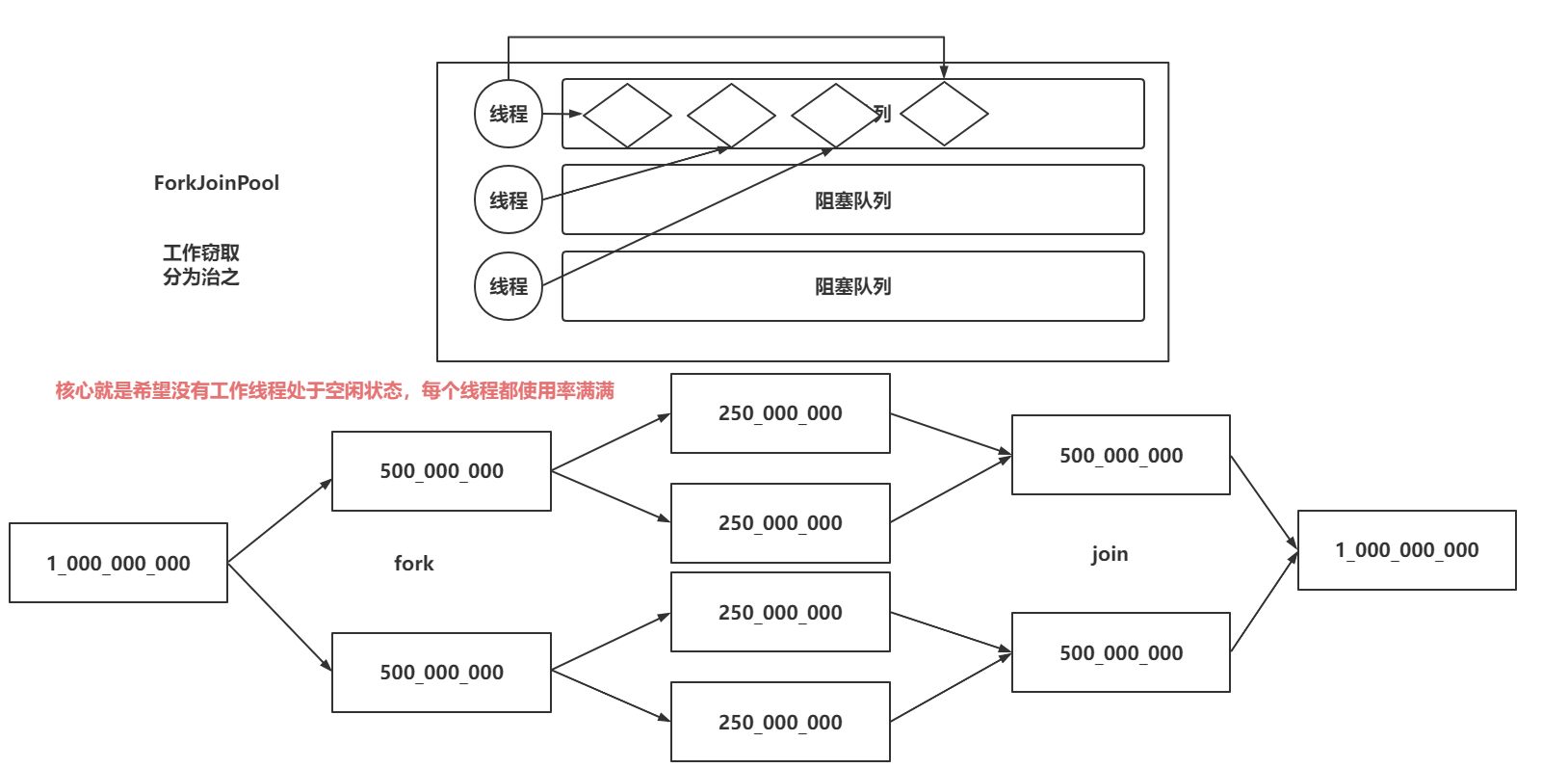
java八股文面试[多线程]——newWorkStealingPool
newWorkStealingPool是什么? newWorkStealingPool简单翻译是任务窃取线程池。 newWorkStealingPool 是Java8添加的线程池。和别的4种不同,它用的是ForkJoinPool。 使用ForkJoinPool的好处是,把1个任务拆分成多个“小任务”,把这…...

STM32--RTC实时时钟
文章目录 Unix时间戳时间戳转换BKPRTC简介RTC框图硬件电路RTC的注意事项RTC时钟实验工程 Unix时间戳 Unix 时间戳是从1970年1月1日(UTC/GMT的午夜)开始所经过的秒数,不考虑闰秒。 时间戳存储在一个秒计数器中,秒计数器为32位/64…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
