5. 自动求导
5.1 向量链式法则

① 例子1是一个线性回归的例子,如下图所示。


5.2 自动求导

5.3 计算图
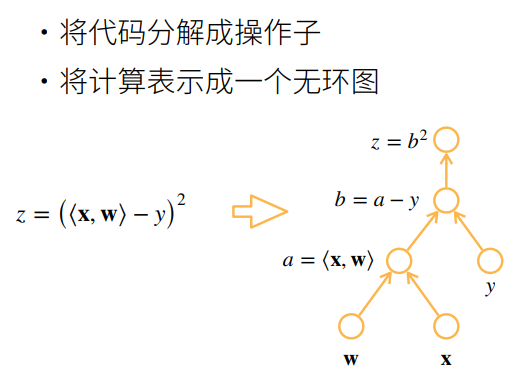


5.4 两种模型


① b是之前计算的结果,是一个已知的值。
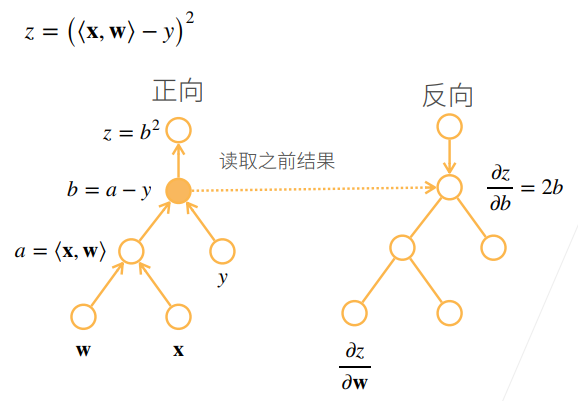



5.5 复杂度

5.6 自动求导
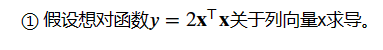
import torch
x = torch.arange(4.0)
x结果:

② 在外面计算y关于x的梯度之前,需要一个地方来存储梯度。
import torch
x = torch.arange(4.0)
x.requires_grad_(True) # 等价于 x = torch.arange(4.0,requires_grad=True)
print(x.grad) # 默认为None结果:(两种写法)

③ 现在计算y。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
print(y) # grad_fn是隐式的构造了梯度函数结果:
④ 通过调用反向传播函数来自动计算y关于x每个分量的梯度。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward() # 反向传播后会有梯度计算出来
print(x.grad) # 访问导数,即访问梯度
print(x.grad == 4 * x) # 4 * x 是 2 * x * x 的导数结果:

⑤ 计算x的另一个函数。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
# 默认情况下,PyTorch会累积梯度,需要清除之前的值
x.grad.zero_() # y.backward() 后才能产生梯度,才能梯度清零,没有反向传播,无法梯度清零
y = x.sum() # 这里的y是一个标量,sum函数其实就是x_1+x_2+...x_n,求偏导自然是全1啊
y.backward()
print(x.grad)结果:

⑥ 在深度学习中,目的不是计算微分矩阵,而是批量中每个样本单独计算的偏导数之和。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
# 默认情况下,PyTorch会累积梯度,需要清除之前的值
# 对非标量调用 'backward' 需要传入一个 'gradient' 参数,该参数指定微分函数
x.grad.zero_()
y = x * x # 这里的y不是一个标量,这是一个向量
print(y)
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward() # y.sum()后就讲向量转为标量了,对标量求导
x.grad结果:

⑦ 将某些计算移动到记录的计算图之外。
import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad.zero_()
y = x * x
print(y)
u = y.detach() # y.detach把y当作一个常数,而不是关于x的一个函数
print(y.detach())
print(u)
z = u * x
z.sum().backward()
x.grad == u结果:

import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x,x)
y.backward()
x.grad.zero_()
y = x * x # 这里的y是关于x的函数
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x结果:

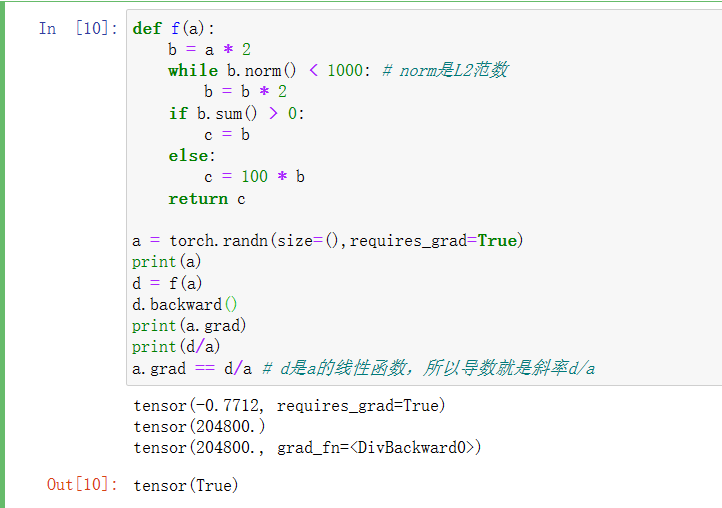
⑧ 即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),仍然可以计算得到的变量的梯度。
def f(a):b = a * 2while b.norm() < 1000: # norm是L2范数b = b * 2if b.sum() > 0:c = belse:c = 100 * breturn ca = torch.randn(size=(),requires_grad=True)
print(a)
d = f(a)
d.backward()
print(a.grad)
print(d/a)
a.grad == d/a # d是a的线性函数,所以导数就是斜率d/a结果:
相关文章:

5. 自动求导
5.1 向量链式法则 ① 例子1是一个线性回归的例子,如下图所示。 5.2 自动求导 5.3 计算图 5.4 两种模型 ① b是之前计算的结果,是一个已知的值。 5.5 复杂度 5.6 自动求导 import torch x torch.arange(4.0) x 结果: ② 在外面计算y关于x的…...

【IEEE会议】 第三届智能通信与计算国际学术会议(ICC 2023)
第三届智能通信与计算国际学术会议 2023 3rd International Conference on Intelligent Communications and Computing 第三届智能通信与计算国际学术会议(ICC 2023)定于2023年11月24-26日在中国南昌隆重举行。会议旨在为从事智能通信与计算研究的专家学…...

巨人互动|Facebook海外户Facebook风控规则有什么
Facebook是全球最大的社交媒体平台之一,每天有数十亿的用户在其上发布、分享和交流各种内容。为了维护平台的安全性和用户体验,Facebook制定了严格的风控规则来监测和处理违规行为。下面小编讲讲Facebook风控规则。 巨人互动|Google海外户&Google Ad…...

pip命令来查看当前激活的虚拟环境
要查看已安装的虚拟环境,您可以使用以下命令: pip freeze该命令将列出所有已安装的包及其版本信息。在虚拟环境中运行时,它将仅显示该虚拟环境中安装的包。 这将列出所有已创建的虚拟环境以及当前激活的环境。 python -m venv list...

STL stack 和 queue
文章目录 一、stack 类和 queue 类的模拟实现 stack 只允许在一端进行插入删除,是一个后进先出(LIFO)的结构,可以存储任意类型 queue 只允许在一端进行插入,另一端进行删除,是一个先进先出(FIFO)的结构,可以存储任意类…...
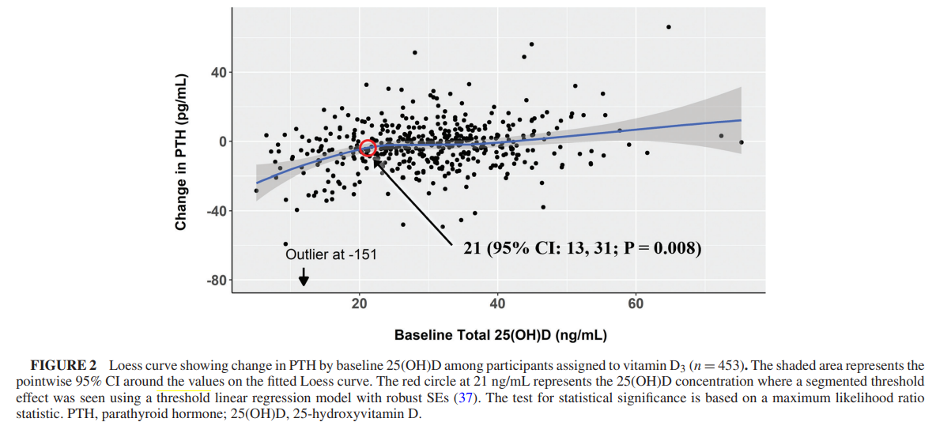
阈值回归模型(Threshold Regression Model)及R实现
阈值回归模型是一类回归模型,其中预测变量与结果以阈值依赖的方式相关联。通过引入一个阈值参数(也称为转折点),阈值回归模型提供了一种简单而优雅、可解释的方法来建立结果和预测变量之间某些非线性关系的模型。在生物医学领域中…...
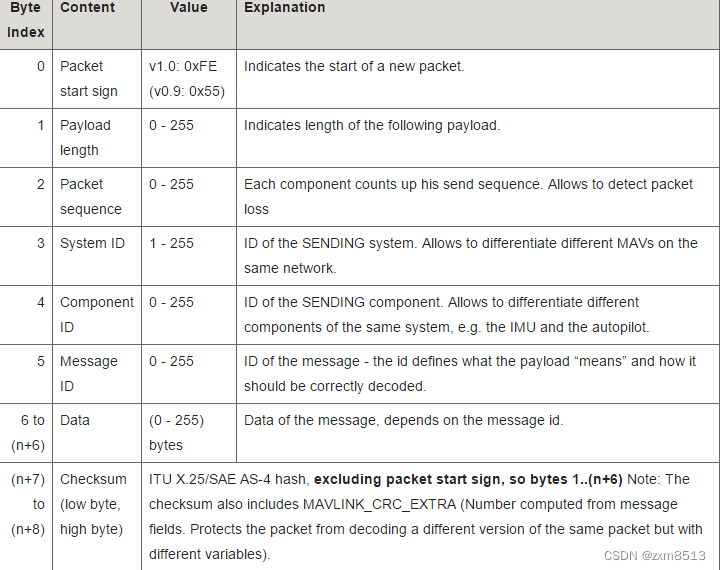
无人机通信协议MAVLink简介
Micro Air Vehicle Link(简称MAVLink)用于无人系统(例如,机器人、无人机、无人车、无人船和无人潜航器)。它定义了一组无人系统和地面站之间的消息交换规则。此协议广泛用于无人驾驶系统中,特别是ArduPilot和PX4无人驾驶系统,MAVLink协议提供了强大的功能,不仅用于监视…...

【办公自动化】用Python批量从上市公司年报中获取主要业务信息
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...
的使用方式】简洁明了初识C语言)
【sizeof()的使用方式】简洁明了初识C语言
sizeof()介绍 sizeof其实仅仅只是一个操作符,我们要注意它并不是一个函数,他就类似与常见的、、-......的操作符,并且sizeof是一个单目操作符。sizeof实际上是获取了数据在内存中所占用的存储空间,以字节为…...

10. 正则表达式匹配
10. 正则表达式匹配 class IsMatch:"""10. 正则表达式匹配https://leetcode.cn/problems/regular-expression-matching/description/"""def solution(self, s: str, p: str) -> bool:m, n len(s), len(p)memo [[-1] * n for _ in range(m)]…...

[Unity]GPU Instancing 无效的原因
参考: GPU Instancing 深入浅出-基础篇(1) - 知乎 Unity GPU Instance踩坑记录_为什么gpuinstance画不出图像_拯救人类的技术宅的博客-CSDN博客 GPUInstancing在真机上失效问题_安卓手机 unity gpu instancing报错__hiJ的博客-CSDN博客 补…...

2023 年前端编程 NodeJs 包管理工具 npm 安装和使用详细介绍
npm 基本概述 npm is the world’s largest software registry. Open source developers from every continent use npm to share and borrow packages, and many organizations use npm to manage private development as well. npm 官方网站:https://www.npmjs.…...
)
ptmalloc源码分析 - Top chunk的扩容函数sysmalloc实现(09)
目录 一、sysmalloc函数基本分配逻辑 二、强制try_mmap分配方式 三、非主分配区分配的实现 1. 设置老的Top chunk的参数 2. 尝试使用grow_heap函数 3. 尝试使用new_heap函数 4. 尝试使用try_mmap方式 四、主分配区分配的实现 1. 设置Top扩容的size值 2. brk分配成功的…...

[BJDCTF2020]ZJCTF,不过如此 preg_replace /e模式漏洞
目录 preg_replace的/e模式 为什么要变为 {${phpinfo()}} 另一个方法 版本 <?phperror_reporting(0); $text $_GET["text"]; $file $_GET["file"]; if(isset($text)&&(file_get_contents($text,r)"I have a dream")){echo &qu…...
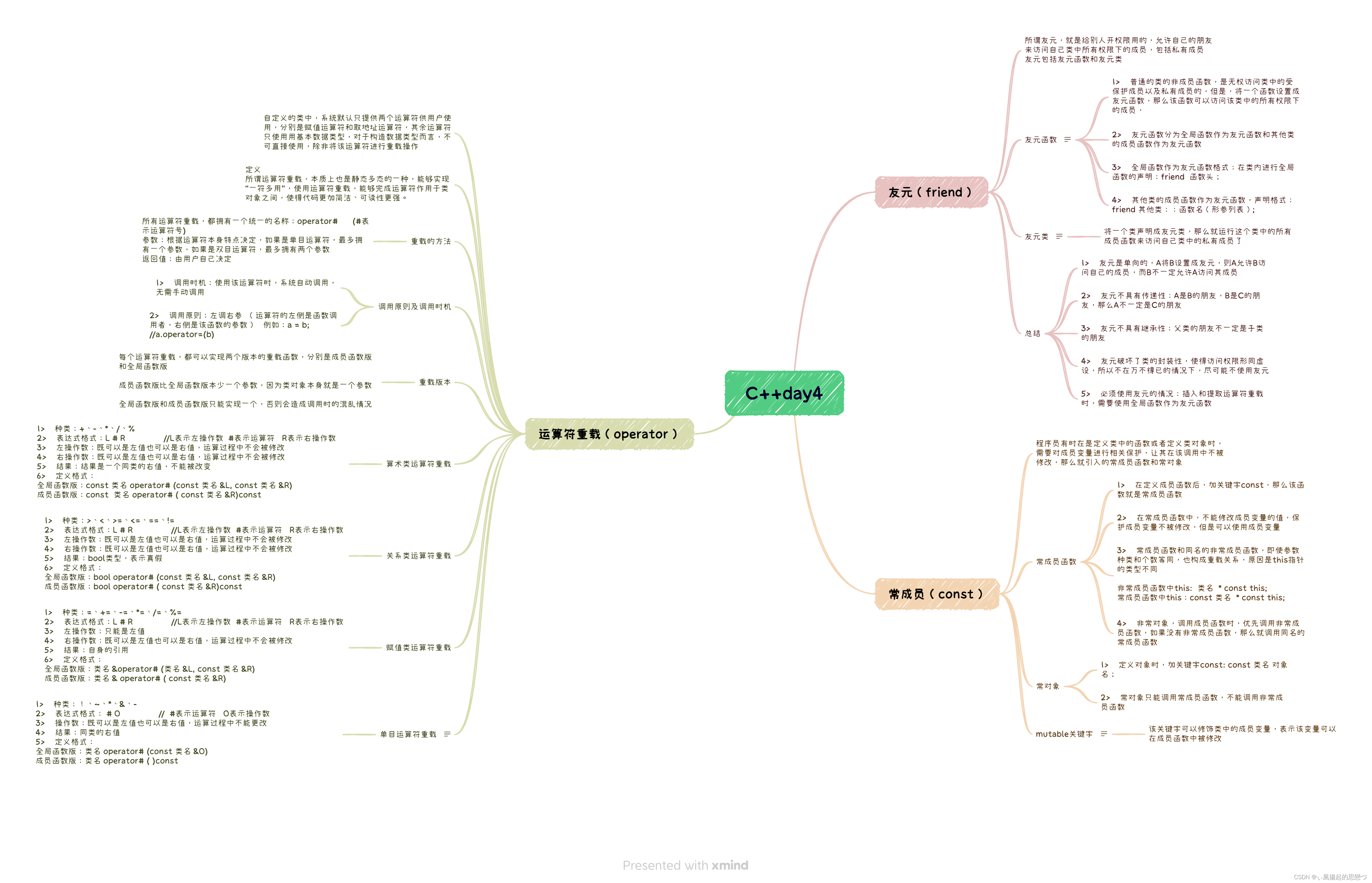
C++day4
1、仿照string类,完成myString 类 #include <iostream> #include <cstring>using namespace std; class myString {private:char *str; //记录c风格的字符串int size; //记录字符串的实际长度public://无参构造myString():size(10…...

【LeetCode-简单题】541. 反转字符串 II
文章目录 题目方法一:双指针 题目 方法一:双指针 题目的意思: 通俗一点说,每隔k个反转k个,末尾不够k个时全部反转; 需要注意右边界的取值 int r Math.min(l k -1,n-1);//取右边界与n-1的最小值 确定边界…...
Linux服务使用宝塔面板搭建网站,并发布公网访问
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

代码随想录算法训练营19期第48天
198.打家劫舍 视频讲解:动态规划,偷不偷这个房间呢?| LeetCode:198.打家劫舍_哔哩哔哩_bilibili 代码随想录 初步思路:动态规划。 总结: dp[i]:考虑下标i(包括i)…...

【校招VIP】产品项目分析之竞品分析
考点介绍: 在产品经理的日常工作当中,经常需要针对某个具体问题或特定功能点进行竞品调研;竞品分析是结构化分析方法论,核心思想是通过对比的方法寻找最佳的解决方案。 产品项目分析之竞品分析-相关题目及解析内容可点击文章末尾…...

【JavaScript内置对象】Date对象,从零开始
【JavaScript内置对象】Date对象,从零开始 时间的表示方式 时间表示的基本概念 最初,人们是通过观察太阳的位置来决定时间的,但是这种方式有一个最大的弊端就是不同区域位置大家使用的时间是不一致的。 相互之间没有办法通过一个统一的时间…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
