Mixin 混入
Mixin 混入
混入 (mixin) 提供了一种非常灵活的方式,来分发 Vue 组件中的可复用功能。一个混入对象可以包含任意组件选项。当组件使用混入对象时,所有混入对象的选项将被“混合”进入该组件本身的选项。
怎么理解呢,就是每一个组件都会有一些选项 data、computed、methods …对吧,假设我有 10 个组件,每一个组件内都有一个相同的 methods 方法,那我就将这个可复用的方法抽离到 mixin 文件中,然后在引入进来。这样我就不需要每个组件都编写重复的 methods 方法了,data、mounted 等等的选项也是如此。
基础案例
hello-world.vue
<template><div class="home">{{ name }}</div>
</template><script>
import mixin from './mixin.js'export default {mixins: [mixin],data() {return {}}
}
</script>
mixin.js
export default {data() {return {name: 'xiaoming'}}
}
预览效果
选项合并
因为混入会把它本身的选项和组件的选项一起合并,那么也就是说会发生一些冲突,例如混入中的文件含有 name 属性,而组件的选项 data 中也存在 name 属性,那页面渲染的时候会以哪个为准呢?接下来进行测试一下。
hello-world.vue
<template><div class="home">{{ name }}</div>
</template><script>
import mixin from './mixin.js'export default {mixins: [mixin],data() {return {name: 'libai'}}
}
</script>
mixin.js
export default {data() {return {name: 'xiaoming'}}
}
预览效果

可以看出来是以组件选项的为准,这里只举例了选项 data 的冲突,其他选项 methods、computed、mounted 也是如此,小伙伴们可以自行去测试一下。在开发的时候需要多留意一下冲突的情况。
原文链接:菜园前端
相关文章:

Mixin 混入
Mixin 混入 混入 (mixin) 提供了一种非常灵活的方式,来分发 Vue 组件中的可复用功能。一个混入对象可以包含任意组件选项。当组件使用混入对象时,所有混入对象的选项将被“混合”进入该组件本身的选项。 怎么理解呢,就是每一个组件都会有一…...

pycharm快捷键
CtrlAltL 代码规范化 CtrlHome 回到代码最开始 CtrlEnd 回到代码最后面 shift回车 鼠标任意位置的下一行 altj 一直按可以选中相同的变量 alt鼠标左键 可以选择多个需要修改的变量或值 将光标放在某一行,home到最前面,end到最后…...

【面试刷题】——Linux基础命令
Linux基础命令是在Linux操作系统中执行常见任务的一组命令。以下是一些常用的Linux基础命令,它们用于管理文件系统、执行系统任务、查看文件内容等。 文件和目录操作: ls: 列出目录中的文件和子目录。 pwd: 显示当前工作目录的路径。 cd: 更改当前工作…...

第四步 Vue2 配置ESLint
ESLint 是一个广泛使用的 JavaScript 代码检查工具,可以帮助开发者在编写代码时发现并修复潜在的问题和错误。 在 第一步 创建工程 时虽然已经选择了包含 ESLint 预设配置,但还需要做一些调整,让我们使用起来能够更加的丝滑。 vue.config.j…...

[.NET学习笔记] - Thread.Sleep与Task.Delay在生产中应用的性能测试
场景 有个Service类,自己在内部实现生产者/消费者模式。即多个指令输入该服务后对象后,Service内部有专门的消费线程执行传入的指令。每个指令的执行间隔为1秒。这里有两部分组成, 工作线程的载体。new Thread与Task.Run。执行等待的方法。…...

【单线图的系统级微电网仿真】基于 PQ 的可再生能源和柴油发电机组微电网仿真(Simulink)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
人脸识别技术应用安全管理规定(试行)|企业采用人脸打卡方式,这4条规定值得关注
近日,为规范人脸识别技术应用,国家互联网信息办公室起草了,并向全社会公开征求意见。该规定一共列举了25条,企业如借助人脸识别技术采集考勤打卡数据,以下4条规定值得关注。 第四条 只有在具有特定的目的和充分的必要…...

leetcode 817. 链表组件(java)
链表组件 题目描述HashSet 模拟 题目描述 给定链表头结点 head,该链表上的每个结点都有一个 唯一的整型值 。同时给定列表 nums,该列表是上述链表中整型值的一个子集。 返回列表 nums 中组件的个数,这里对组件的定义为:链表中一段…...
分布式事务基础理论
基础概念 什么是事务 什么是事务?举个生活中的例子:你去小卖铺买东西,“一手交钱,一手交货”就是一个事务的例子,交钱和交货必 须全部成功,事务才算成功,任一个活动失败,事务将撤销…...

《打造高可用PostgreSQL:策略与工具》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

【八大经典排序算法】快速排序
【八大经典排序算法】快速排序 一、概述二、思路实现2.1 hoare版本2.2 挖坑法2.3 前后指针版本 三、优化3.1 三数取中3.1.1 最终代码3.1.2 快速排序的特性总结 四、非递归实现快排 一、概述 说到快速排序就不得不提到它的创始人 hoare了。在20世纪50年代,计算机科学…...

vue 父组件给子组件传递一个函数,子组件调用父组件中的方法
vue 中父子组件通信,props的数据类型可以是 props: {title: String,likes: Number,isPublished: Boolean,commentIds: Array,author: Object,callback: Function,contactsPromise: Promise // or any other constructor }在父组件中,我们在子组件中给他…...
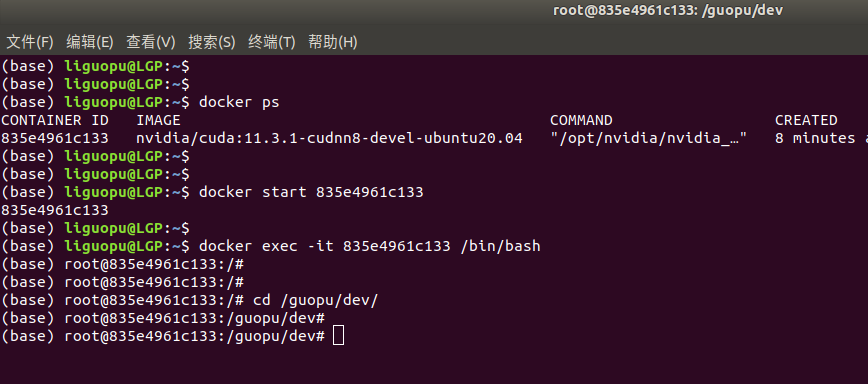
docker 获取Nvidia 镜像 | cuda |cudnn
本文分享如何使用docker获取Nvidia 镜像,包括cuda10、cuda11等不同版本,cudnn7、cudnn8等,快速搭建深度学习环境。 1、来到docker hub官网,查看有那些Nvidia 镜像 https://hub.docker.com/r/nvidia/cuda/tags?page2&name11.…...
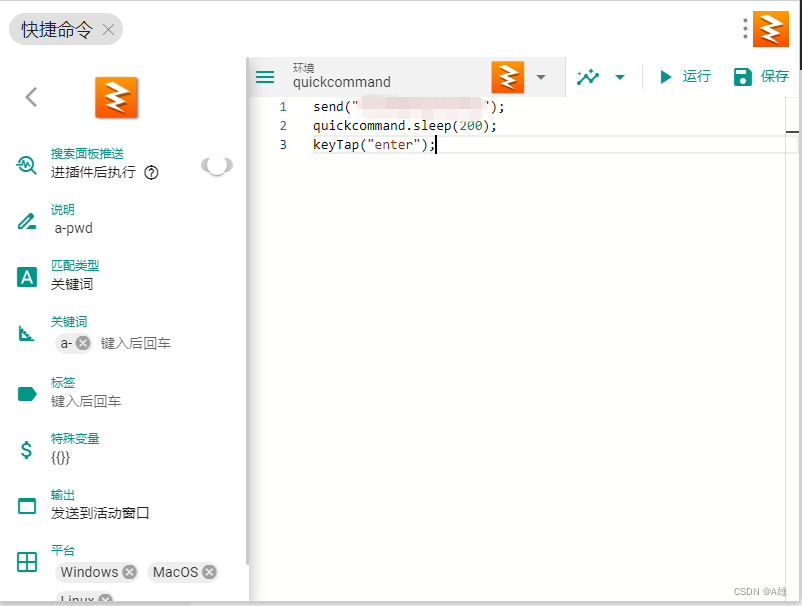
uTool快捷指令
send("************"); quickcommand.sleep(200); keyTap("enter");...

R reason ‘拒绝访问‘的解决方案
Win11系统 安装rms的时候报错: Error in loadNamespace(j <- i[[1L]], c(lib.loc, .libPaths()), versionCheck vI[[j]]) : namespace Matrix 1.5-4.1 is already loaded, but > 1.6.0 is required## 安装rms的时候报错,显示Matrix的版本太低…...

许战海战略文库|品类缩量时代:制造型企业如何跨品类打造份额产品?
所有商业战略的本质是围绕着竞争优势与竞争效率展开的。早期,所有品牌立足于从局部竞争优势出发。因此,品牌创建初期大多立足于单个品类。后期增长受限,就要跨品类持续扩大竞争优势,将局部竞争优势转化为长期竞争优势,如果固化不前很难获得增…...
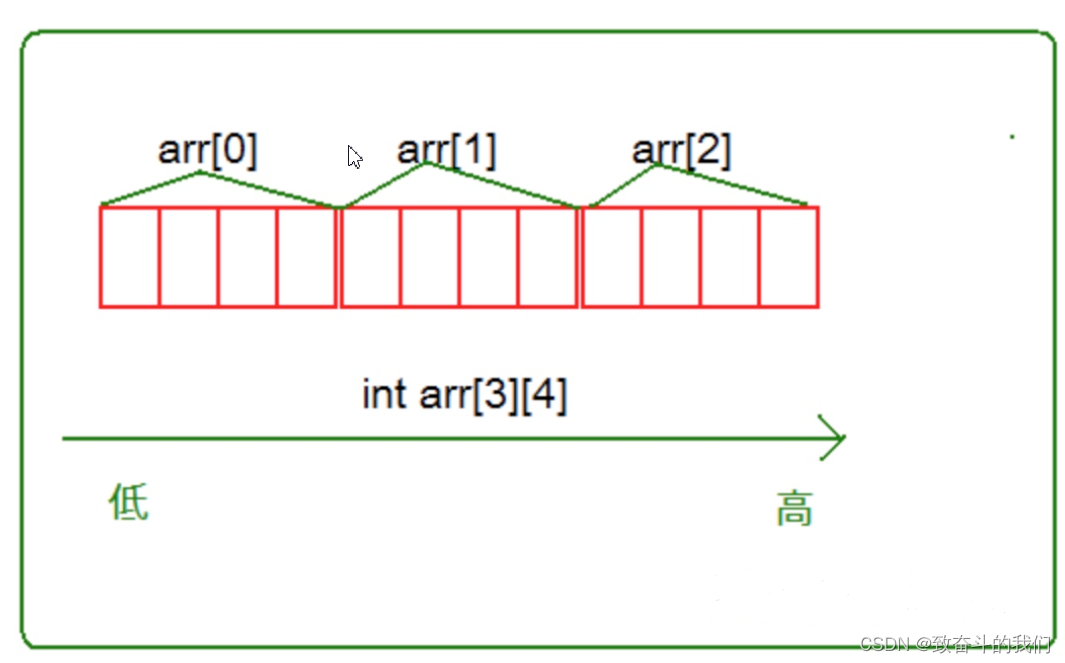
BIT-4-数组
一维数组的创建和初始化一维数组的使用 一维数组在内存中的存储 二维数组的创建和初始化二维数组的使用二维数组在内存中的存储 数组越界数组作为函数参数数组的应用实例1:三子棋 数组的应用实例2:扫雷游戏 1. 一维数组的创建和初始化 1.1 数组的创建 …...
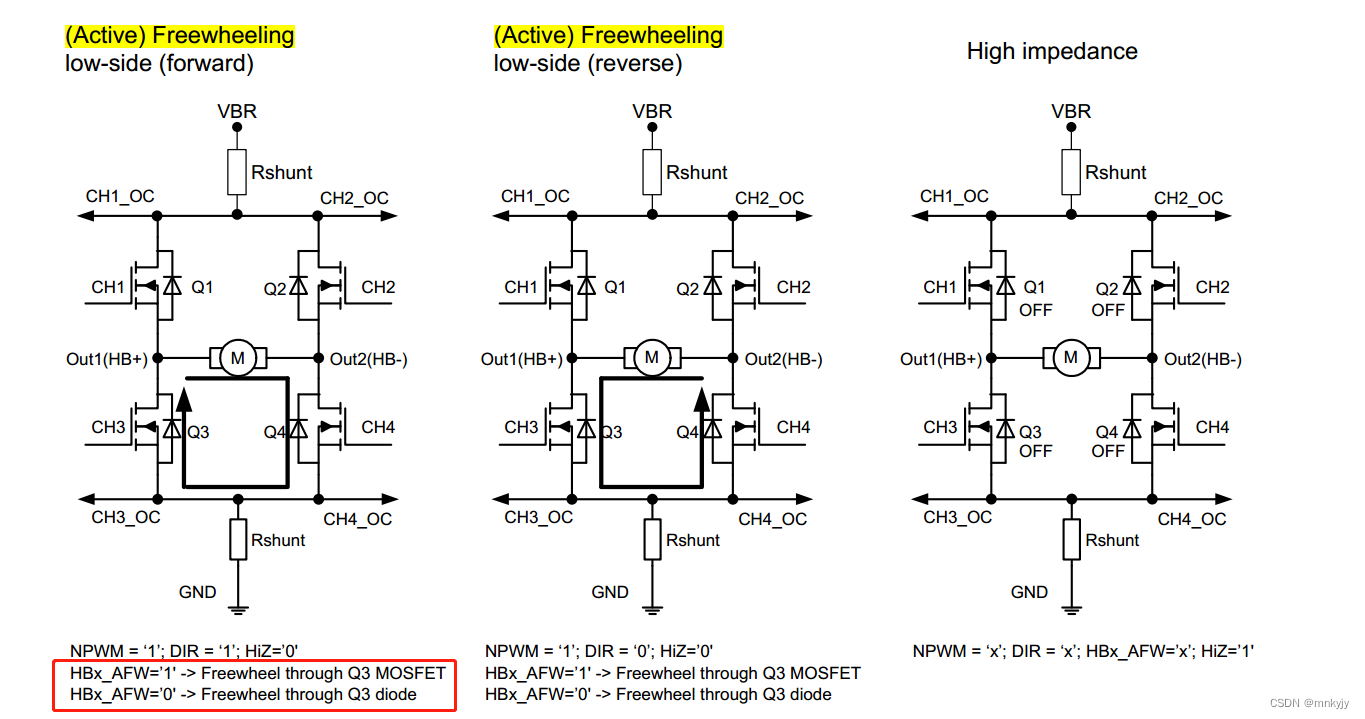
L9945的H桥续流模式
在H桥的配置中,包括两种续流模式:主动续流和被动续流。 一个L9945可输出两个H桥驱动。HB1在CMD3中配置,HB2在CMD7中配置。 主动续流:通过Q3的MOS的二极管来续流 被动续流:通过Q3外部的二极管来续流...
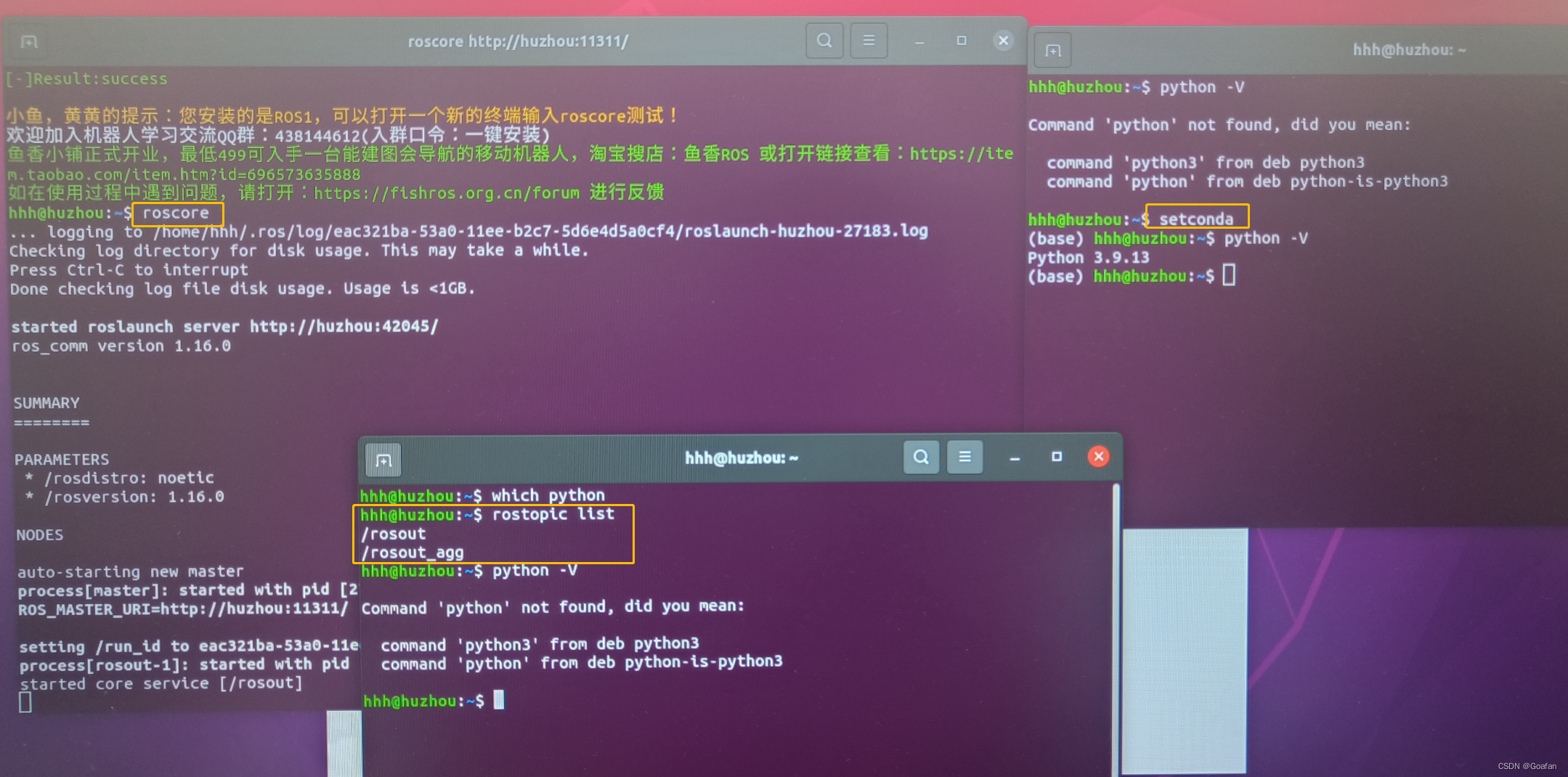
Ubuntu20.04安装Nvidia显卡驱动、CUDA11.3、CUDNN、TensorRT、Anaconda、ROS/ROS2
1.更换国内源 打开终端,输入指令: wget http://fishros.com/install -O fishros && . fishros 选择【5】更换系统源,后面还有一个要输入的选项,选择【0】退出,就会自动换源。 2.安装NVIDIA驱动 这一步最痛心…...

linux下使用crontab定时器,并且设置定时不执行的情况,附:项目启动遇到的一些问题和命令
打开终端,以root用户身份登录。 运行以下命令打开cron任务编辑器: crontab -e 如果首次编辑cron任务,会提示选择编辑器。选择你熟悉的编辑器,比如nano或vi,并打开相应的配置文件。 在编辑器中,添加一行类…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...
