【每日一题Day335】LC1993树上的操作 | dfs
树上的操作【LC1993】
给你一棵
n个节点的树,编号从0到n - 1,以父节点数组parent的形式给出,其中parent[i]是第i个节点的父节点。树的根节点为0号节点,所以parent[0] = -1,因为它没有父节点。你想要设计一个数据结构实现树里面对节点的加锁,解锁和升级操作。数据结构需要支持如下函数:
**Lock:**指定用户给指定节点 上锁 ,上锁后其他用户将无法给同一节点上锁。只有当节点处于未上锁的状态下,才能进行上锁操作。
**Unlock:**指定用户给指定节点 解锁 ,只有当指定节点当前正被指定用户锁住时,才能执行该解锁操作。
Upgrade:
指定用户给指定节点
上锁
,并且将该节点的所有子孙节点
解锁
。只有如下 3 个条件
全部
满足时才能执行升级操作:
- 指定节点当前状态为未上锁。
- 指定节点至少有一个上锁状态的子孙节点(可以是 任意 用户上锁的)。
- 指定节点没有任何上锁的祖先节点。
请你实现
LockingTree类:
LockingTree(int[] parent)用父节点数组初始化数据结构。lock(int num, int user)如果 id 为user的用户可以给节点num上锁,那么返回true,否则返回false。如果可以执行此操作,节点num会被 id 为user的用户 上锁 。unlock(int num, int user)如果 id 为user的用户可以给节点num解锁,那么返回true,否则返回false。如果可以执行此操作,节点num变为 未上锁 状态。upgrade(int num, int user)如果 id 为user的用户可以给节点num升级,那么返回true,否则返回false。如果可以执行此操作,节点num会被 升级 。
-
思路
使用数组记录每个节点的父节点以及上锁状态,并使用list记录每个节点的孩子节点,方便dfs操作
- lock和unlock函数进行简单判断即可
- upgrade函数需要判断祖先节点是否上锁,再通过dfs判断是否有上锁的孩子节点,并将其解锁
-
实现
class LockingTree {// 记录每个节点的根节点以及加锁状态int[] locked;int[] parent;int n;List<Integer>[] children;public LockingTree(int[] parent) {this.n = parent.length;this.parent = parent;this.locked = new int[n];this.children = new List[n];Arrays.fill(locked, -1);Arrays.setAll(children, e -> new ArrayList<>());for (int i = 0; i < n; i++){if (parent[i] != -1){children[parent[i]].add(i);}}}public boolean lock(int num, int user) {if (locked[num] != -1) return false;locked[num] = user;return true;}public boolean unlock(int num, int user) {if (locked[num] == user){locked[num] = -1;return true;}return false;}public boolean upgrade(int num, int user) {if (locked[num] != -1) return false;// 判断祖先节点是否上锁int p = parent[num];while (p != -1){if (locked[p] != -1) return false;p = parent[p];}// 判断是否有子孙节点加锁了,并给子孙节点解锁boolean[] res = {false};dfs(num, res);if (res[0] == false) return false;locked[num] = user;return true;}public void dfs(int p, boolean[] lock){for (int u : children[p]){if (locked[u] != -1){lock[0] = true;locked[u] = -1; }dfs(u, lock);}} }/*** Your LockingTree object will be instantiated and called as such:* LockingTree obj = new LockingTree(parent);* boolean param_1 = obj.lock(num,user);* boolean param_2 = obj.unlock(num,user);* boolean param_3 = obj.upgrade(num,user);*/- 复杂度
- 时间复杂度: n n n为二叉树的节点数目,lock和unlock为 O ( n ) \mathcal{O}(n) O(n),upgrade为 O ( 1 ) \mathcal{O}(1) O(1)
- 空间复杂度: O ( n ) \mathcal{O}(n) O(n)
- 复杂度
相关文章:

【每日一题Day335】LC1993树上的操作 | dfs
树上的操作【LC1993】 给你一棵 n 个节点的树,编号从 0 到 n - 1 ,以父节点数组 parent 的形式给出,其中 parent[i] 是第 i 个节点的父节点。树的根节点为 0 号节点,所以 parent[0] -1 ,因为它没有父节点。你想要设计…...

FPGA:卷积编码及维特比译码仿真
FPGA:卷积编码及维特比译码仿真 本篇记录一下在FPGA中完成卷积编码和维特比译码的过程,通过代码解释编码的过程和译码的过程,便于理解,同时也方便移植到其他工程中。 1. 准备工作 卷积编译码IP核—convolutionIP核和viterbiIP核…...
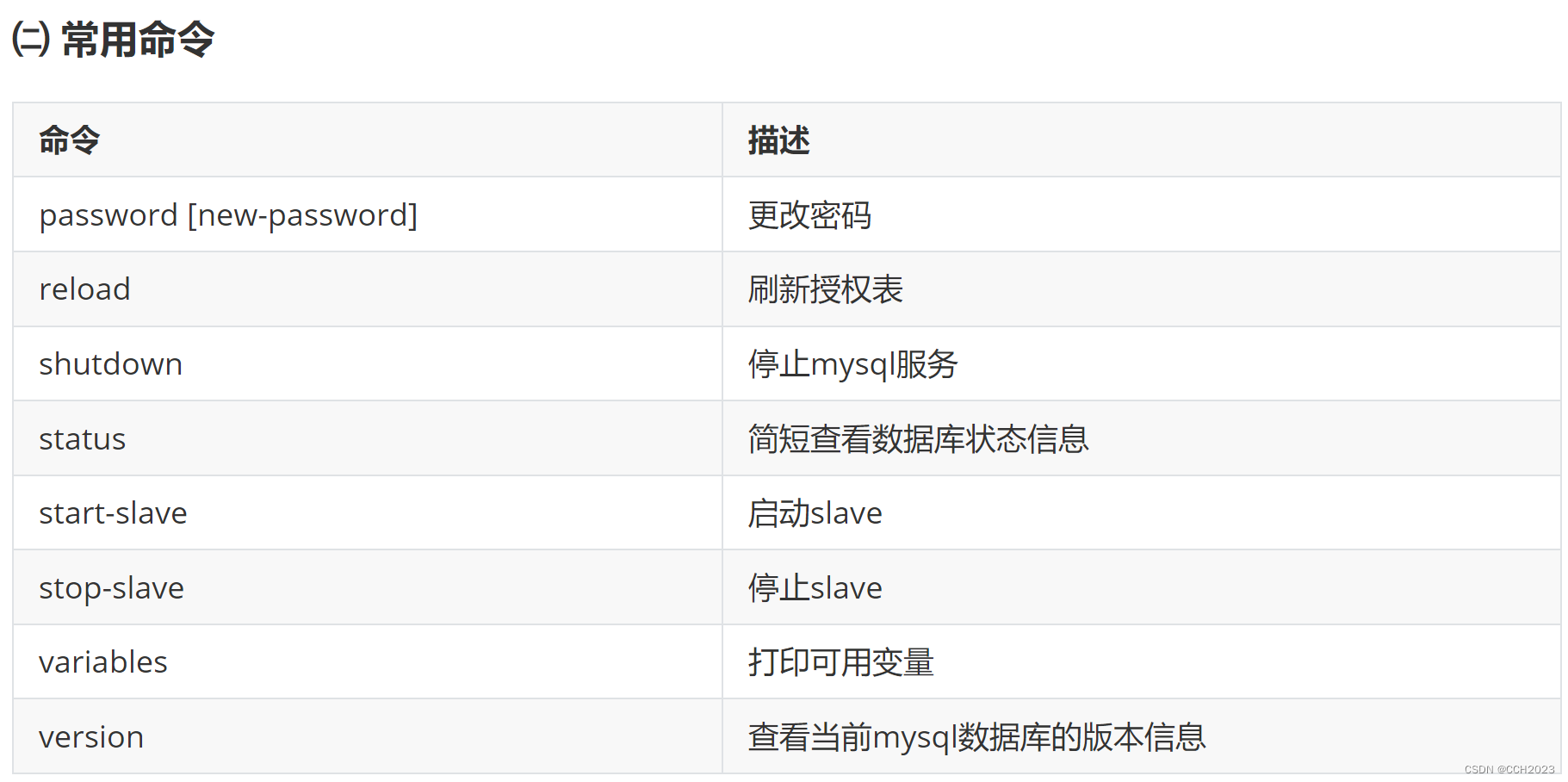
MySQL学习笔记4
客户端工具的使用: MySQL: mysql命令行工具,一般用来连接访问mysql的数据。 案例:使用mysql客户端工具连接服务器端(用户名:root;密码:123456). [rootmysql-server ~]#…...

JavaFX:窗体显示状态,模态非模态
程序窗体显示一般有3中模式。非模态和模态,其中模态又分为程序模态和窗体模态。 非模态可以理解为窗体之间没有任何限制,可以用鼠标、键盘等工具在窗体间切换。 程序模态是窗体打开后,该程序的所有窗体都被冻结,无法切换&#x…...
C++17中std::filesystem::path的使用
C17引入了std::filesystem库(文件系统库, filesystem library)。这里整理下std::filesystem::path的使用。 std::filesystem::path,文件系统路径,提供了对文件系统及其组件(例如路径、常规文件和目录)执行操作的工具。此path类主要用法包括&#x…...

命令模式简介
概念: 命令模式是一种行为设计模式,它将请求封装成一个对象,从而允许您将不同的请求参数化、队列化,并且能够在不同的时间点执行。通过引入命令对象(Command)来解耦发送者(Invoker)…...

Boost序列化指针
Boost.Serialization 还能序列化指针和引用。 由于指针存储对象的地址,序列化对象的地址没有什么意义,而是在序列化指针和引用时,对象的引用被自动地序列化。 代码 #include <boost/archive/text_oarchive.hpp> #include <boost/…...
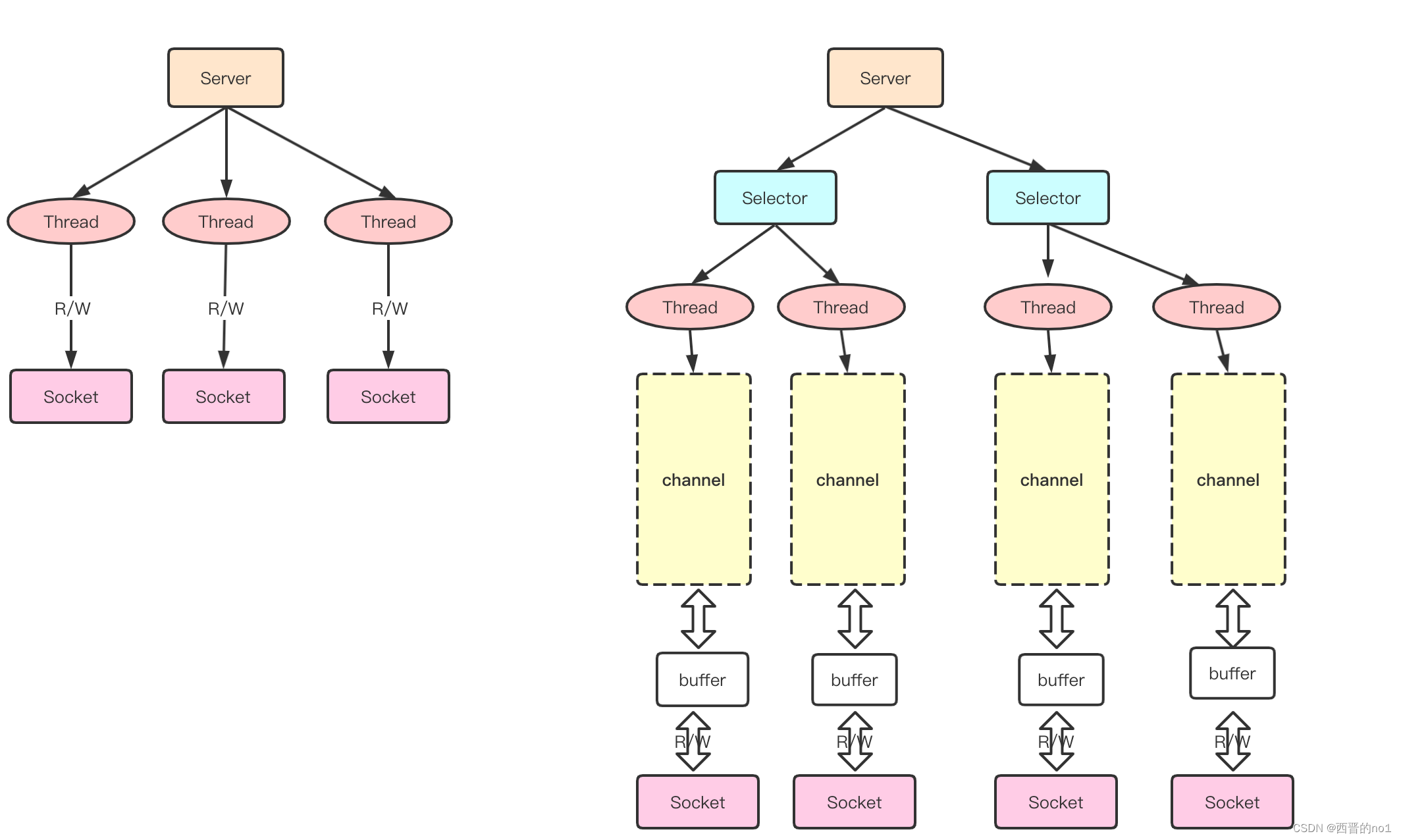
NIO简单介绍
一、什么是NIO 1、Java NIO全称java non-blocking IO, 是指JDK提供的新API。从JDK1.4开始,Java提供了一系列改进的输入/输出的新特性,被统称为NIO(即New IO),是同步非阻塞的 2、NIO有三大核心部分: Channel(通道), Buf…...
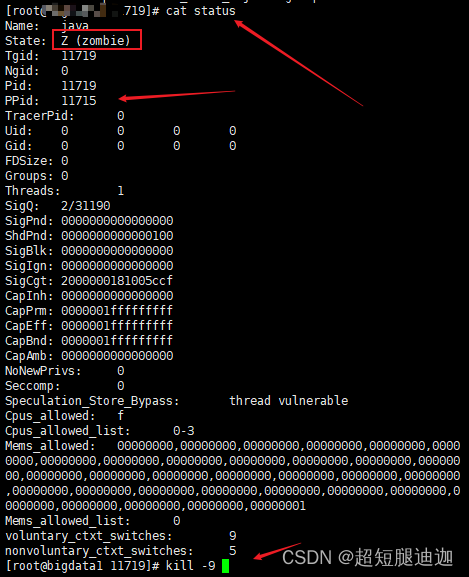
linux进程杀不死
项目场景: 虚拟机 问题描述 linux进程杀不死 无反应 原因分析: 进程僵死zombie 解决方案: 进proc或者find命令找到进程所在地址 cat status查看进程杀死子进程...

5分钟带你搞懂RPA到底是什么?RPA能做什么?
一、RPA的定义 RPA,全称Robotic Process Automation,即机器人流程自动化,是一种软件解决方案,能够模拟人类在计算机上执行的操作,以实现重复性、繁琐任务的自动化。它与传统的计算机自动化有所不同,因为它…...
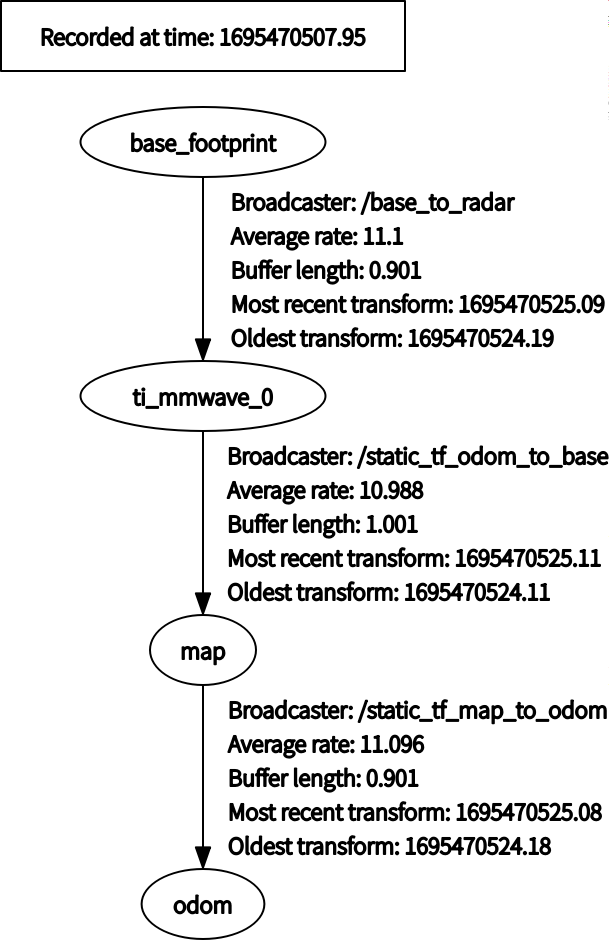
毫米波雷达 TI IWR1443 在 ROS 中进行 octomap 建图
个人实验记录 /mmwave_ti_ros/ros_driver/src/ti_mmwave_rospkg/launch/1443_multi_3d_0.launch <launch><!-- Input arguments --><arg name"device" value"1443" doc"TI mmWave sensor device type [1443, 1642]"/><arg…...

113双周赛
题目列表 2855. 使数组成为递增数组的最少右移次数 2856. 删除数对后的最小数组长度 2857. 统计距离为 k 的点对 2858. 可以到达每一个节点的最少边反转次数 一、使数组成为递增数组的最少右移次数 这题可以直接暴力求解,枚举出每种右移后的数组,将…...
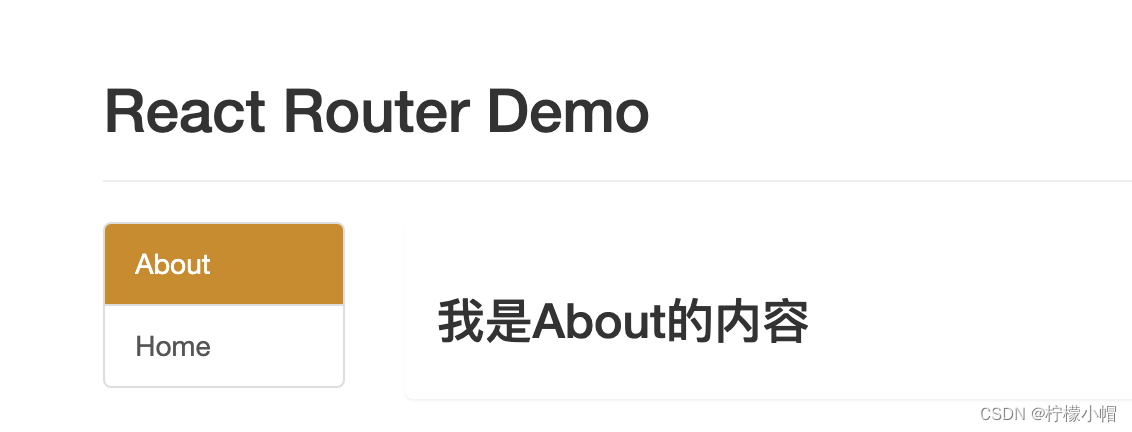
React 全栈体系(九)
第五章 React 路由 一、相关理解 1. SPA 的理解 单页 Web 应用(single page web application,SPA)。整个应用只有一个完整的页面。点击页面中的链接不会刷新页面,只会做页面的局部更新。数据都需要通过 ajax 请求获取, 并在前端…...
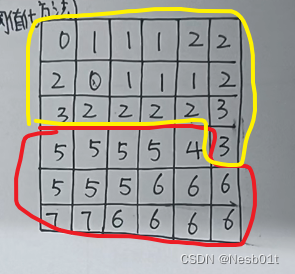
阈值化分割,对灰度级图像进行二值化处理(数字图像处理大题复习 P8)
文章目录 画出表格求出灰度直方图 & 山谷画出结果图 画出表格 有几个0就写几,有几个1就写几,如图 求出灰度直方图 & 山谷 跟前面求灰度直方图的方法一样,找出谷底,发现结果为 4 画出结果图 最终的结果就是…...

vue3中withDefaults是什么
问: const props withDefaults(defineProps<{// 数据列表lotteryList: { pic: string; name?: string }[];// 中奖idwinId: number;// 抽奖初始转动速度initSpeed: number;// 抽奖最快转动速度fastSpeed: number;// 抽奖最慢转动速度slowSpeed: number;// 基本圈数baseCi…...
Android进阶之路 - 盈利、亏损金额格式化
在金融类型的app中,关于金额、数字都相对敏感和常见一些,在此仅记录我在金融行业期间学到的皮毛,如后续遇到新的场景也会加入该篇 该篇大多采用 Kotlin 扩展函数的方式进行记录,尽可能熟悉 Kotlin 基础知识 兄弟 Blog StringUti…...
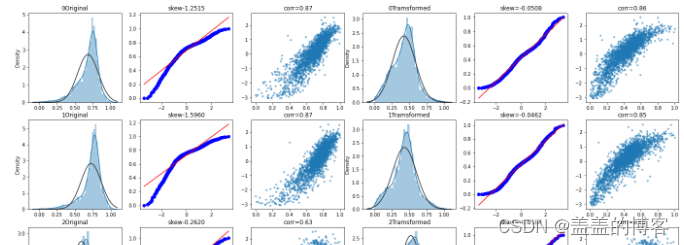
工业蒸汽量预测(速通一)
工业蒸汽量预测(一) 赛题理解1、评估指标2、赛题模型3、解题思路 理论知识1、变量识别2、变量分析3、缺失值处理4、异常值处理5、变量转换6、新变量生成 数据探索1、导包2、读取数据3、查看数据4、可视化数据分布4.1箱型图4.2获取异常数据并画图4.3直方图…...

机器学习的主要内容
分类任务 回归任务 有一些算法只能解决回归问题有一些算法只能解决分类问题有一些算法的思路既能解决回归问题,又能解决分类问题 一些情况下, 回归任务可以转化为分类任务, 比如我们预测学生的成绩,然后根据学生的成绩划分为A类、…...
)
华为OD机试真题-分积木-2023年OD统一考试(B卷)
题目描述: Solo和koko是两兄弟,妈妈给了他们一大堆积木,每块积木上都有自己的重量。现在他们想要将这些积木分成两堆。哥哥Solo负责分配,弟弟koko要求两个人获得的积木总重量“相等”(根据Koko的逻辑),个数可以不同,不然就会哭,但koko只会先将两个数转成二进制再进行加…...

SpringBoot自动装配原理及分析
一、什么是自动装配 在使用SpringBoot的时候,会自动将Bean装配到IoC容器中。例如我们在使用Redis数据库的时候,会引入依赖spring-boot-starter-data-redis。在引入这个依赖后,服务初始化的时候,会将操作Redis需要的组件注入到IoC…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
