C++ - 红黑树 介绍 和 实现
前言
前面 学习了 AVL树,AVL树虽然在 查找方面始终拥有 O(log N )的极高效率,但是,AVL 树在插入 ,删除等等 修改的操作当中非常的麻烦,尤其是 删除操作,在实现当中细节非常多,在实现上非常难掌控。具体可以看以下两篇文章:
C++ - AVL 树 介绍 和 实现 (上篇)_chihiro1122的博客-CSDN博客
C++ - AVL树实现(下篇)- 调试小技巧_chihiro1122的博客-CSDN博客
而 红黑树 在构建就下个对容易一些了。
红黑树 介绍
红黑树和 AVL树一样,都是 二叉平衡搜索树,红黑树的构建是在 每个结点除了 孩子的链接关系,和值以外,加一个位置存储该结点的颜色,一个结点的颜色只有 red 和 black 两种。红黑树通过对 任意一条路径上的各个结点的颜色限制,确保没有一条路径会比其他路径长出两倍。

相比于 AVL树,红黑树对于平衡的要求更加宽松,他只是要求最长路径最多是 最短路径的两倍;
而 AVL树 是严格限死了 左右子树高度不能超过 2 。
也就是说,红黑树在高度上 要比 AVL树要高一些。
虽然 红黑树 在平衡上更加的宽松,但是实际的效率却依旧非常的高,并不比 AVL树差,至于为什么我们在下述来验证。
而且 ,红黑树不会进行 旋转,尽管在 AVL树当中旋转是常量级的,但是,数量多了之后,还是有很多的消耗。
在AVL树当中,插入和删除都要经过很多次的旋转。也就造成不小的消耗。
而 AVL树 相比于 红黑树 多出来的消耗在 红黑树看来是没有必要的。
如下图当中的分析:

红黑树树的性质(规则)
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点必须是黑色的 。(每一条从根结点开始的路径,没有重复的红色结点)
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点。(红黑树当中每一条路径上,黑色结点数是相同的)(在一条路径当中,黑色结点的占比一定 大于 或 等于 1 /2 )
- 每一个 “叶子结点” 都是黑色的,注意:此处的叶子结点不是我们以前理解的 最后一个结点,在红黑树当中的 这里的 “叶子结点” 实际上是最后一个 NULL 结点(所有的 NIL 结点都是 黑色的)。如下图所示:

在红黑树当中,对 这个 NULL 结点进行了重新定义,取名为 NIL 结点,而且我们上述所说的路径,是指:从根结点到最后的 NIL 结点,为一条路径。
就比如上述,如果不加上 NULL ,那么计算出来的路径数目就是 5 条;但是如果加上 NULL ,来计算的话就是 11 条,而11 跳才是正确。
也就是说,如果你不加上最后一个 NULL 结点来用 红黑树的规则来判断 一颗树是不是红黑树的话,机会出错,比如下述例子:

如果,你按照我们以前认为,最后一个结点就是叶子结点,而且在算上路径时候没有加上最后的NULL。那么你就会认为,这是一颗红黑树;
但,实际上这不是一颗红黑树。
其实,按照上述 的 第五条性质,其实就是在每一条路径的后面都加上了 一个 黑色结点。
insert()插入函数
首先我们来想一下,当一颗红黑树当中已经有结点了,如下所示,那么当我们插入一个结点是插入红色的结点还是 插入一个黑色的结点好呢?


如果插入 黑色结点就会违反 条件4,;如果插入 红色结点就会违反 条件3;
如果要违反条件的话,可能是违反 条件3更好。
因为 ,如果违反条件4,就会影响全部路径;而如果 违反条件3 就只会 影响一个路径,不会是全部路径。
如下所示,我们插入一个黑色结点:

在插入A结点之后,到A结点的这条路径的 黑色结点的个数就 +1了,但是其他路径上都没有变化,此时就影响到其他 路径了。
但是如果插入的是一个红色的结点,只影响一个路径,所以,当发生错误的时候我们可以修正:

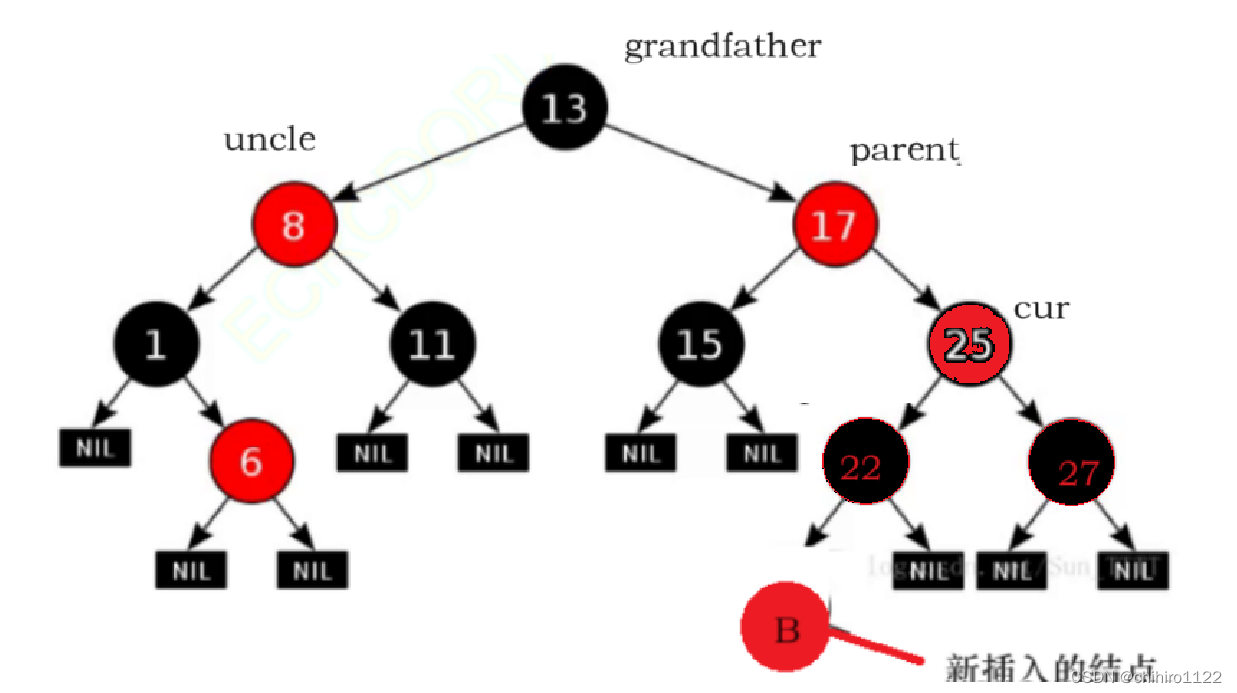
上述插入的B结点,在 22 的下面,22 是红色结点,这个位置就不行但是如果是插入在 15 的下面,15 是一个黑色的结点,是可以的。
如果 红色结点 B 插入到 22 的下面,此时 B 的父亲结点是 红色的,说明B 一定会有 父亲的父亲,也就是说 grandfather。因为 整棵树只有根结点才没有父亲,而根结点必须是 黑色的:

如上所示,红色结点一定有 父亲。也就是说,出现上述情况的话,grandfather 结点是肯定存在的。
红黑树的插入,修改过程
我们上述讨论了,插入的结点必须是红色的结点,插入红色的结点的话,就会影响到父亲(新插入结点的路径)。
具体例子理解
所以,此时我们要从该路径上进行修改。
此时违法的规则就是 B 和 22 两个红色结点连在一起了,所以我们就想着把 22 边黑,但是变黑的话,就会影响这棵树当中的黑节点个数。
所以,在更新完 25 这颗子树之后,可能会像 AVL 树当中的平衡因子一样往上更新的。
如上述图,单次对于子树的修改:
需要先找到 新插入结点 父亲的 亲兄弟(uncle)。如果 uncle 存在且为 红,那么就把 parent 和 uncle 都变 黑:
但是此时我们发现,变黑之后,对于 22 和 27 这两条路径来说,黑色结点个数相比于其他路径,在增多了一个,所以,此时我们在让 grandfather 结点变红,就可以解决黑色结点个数问题:
但是,对于 grandfather 结点不一定都是这种的处理方法:
- 如果 grandfather 结点没有父亲,说明此时 grandfather 结点是 整棵树的根结点,那么把 grandfather 结点变红就行。
- 如果 grandfather 有父亲,grandfather 是 黑色,就结束了。
- 如果 grandfather 有父亲,grandfather 是 红色,有和上述问题一样了,需要找 uncle。
我们继续来看上述例子:
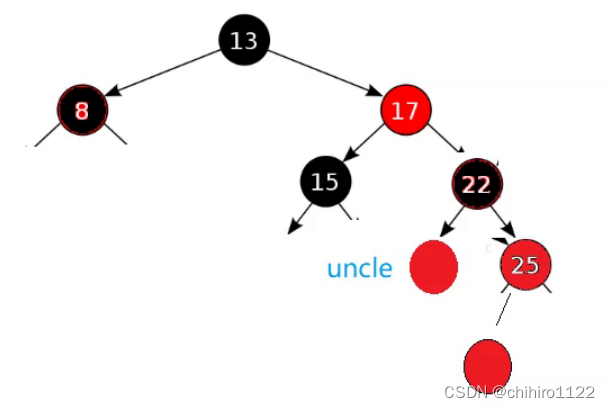
在上述修改之后, 发现 17 和 25 又是两个红色结点链接在一起了,此时就要对这个链接关系进行修改,此时就好比是 新插入了 25 结点。
找 uncle(8),uncle 为红,就把 parent 和 uncle 一起改为黑,此时的 grandfather 没有父亲结点了,就不用再变黑了:
如果按照上述的过程来修改的话,我们发现,相当于是在每一条路径当中都增加了一个 黑色结点。
黑色结点其实是有好处的,比如上述的例子的那种,我们插入的新结点一定是 红色的,那么插入在黑色结点后面就不用像上述一样进行修改,如上图所示,我们只有在 6 后面和在 B 后面插入结点才会像上述一样进行修改。
上述是 有uncle的情况,如果 parent 没有亲兄弟,也就是 cur 没有 uncle的话,应该怎么办呢?
如上述所示,cur 没有 uncle,我们不能直接把 parent 变黑,因为会多出一个 黑色结点;有人又说,多出来一个黑色结点的话,把 grandfather 在变 红不就行了,但是 如果把 grandfather 变红的话,指向 uncle 的路径上就少一个 黑色结点了。
而且我们发现,如果在 cur 位置插入的话,13 的右子树的上的路径长度已经比 左子树 上的路径长度多出 2 倍了。
所以,不管是否 多出 2 倍,在没有 uncle的情况下,我们应该进行旋转来调整位置。
判断旋转方式还是和在 AVL树当中判断方式一样,旋转方式请看一下博客:
C++ - AVL 树 介绍 和 实现 (上篇)_chihiro1122的博客-CSDN博客
像上述,就是发生了的右单旋,但是旋转之后发现,颜色上还是 违反了规则。
所以此时要变色。
所以,当uncle 不存在的时候,处理规则就是 旋转 + 变色。
uncle存在且为红的情况,在修改之后也有可能会出现 最长路径和最短路径 长度超过两倍的情况(uncle 为黑的情况):
修改:
此时我们发现,如果我们单纯的把 17 变黑,已经不能解决问题了,此时也是需要旋转的。
13 的右子树已经明显的高了,要对右子树进行旋转,此时发生左单旋。如果是下述情况就是 双旋:
cur , parent , grandfather 构成折线,就要发生双旋。
但是,在 AVL 树当中我们判断旋转的方式是利用 平衡因子的方式来判断的,但是在红黑树当中没有平衡因子,我们需要判断 cur , parent , grandfather 三者的链接关系来 确认要哪一种旋转。
我没发现,红黑树优势不仅仅在于旋转变少了,他是在修改过程当中就会把很多结点变黑,那么在以后插入当中,插入到黑节点后面就不必再进行修改了。
小总结:
红黑树的插入,关键看 uncle。
- 如果 uncle 存在且为红,变色+ 往上进行处理
- 如果 uncle存在且为黑,旋转+变色+往上进行处理
- 如果 uncle不存在,旋转 + 变色 + 往上进行处理
抽象图理解 红黑树插入过程
按照上述说明,出现需要修改的情况,都是 红红黑的结构,也就是 cur 为红, parent 为红,grandfather 为黑的情况,而修改过程当中,判别不用的修改方式,是看 uncle 的。
我们先来总结一下 解决方案:
- 情况一: cur为红,p为红,g为黑,u存在且为红。 解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
- 情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑。 解决方法:p为g的左孩子,cur为p的左孩子,则进行右单旋转; p为g的右孩子,cur为p的右孩子,则进行左单旋转。 p为g的左孩子,cur为p的右孩子,则针对p做左单旋转; p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
具体情况分析:
情况一:
比如上述是 的抽象图,他可能是 一颗子树,也可能是 整棵树。
那么,当我们在 a ,b 后面插入的话,可能就会应发 情况一:
当 c/d/e 子树每条路径当中只有 一个 黑色结点:
如上述情况我们就要使用 情况一的处理方式了。
对于情况一,因为不旋转,对于新结点的插入位置,是不管的,主要是 在 a 和 b 的四个位置插入都是引发情况一,或者不引发。
至于 cur 可能本来就是 grandfather 的黑色结点,只是在 a,b当中没有个进行修改,把 grandfather 修改为了 红色。
当然,还有 cur 本来就是 新增结点的情况,也就是 a 和 b 两个子树都是 空:
但是处理方式还是情况一的方式。
当 c/d/e 子树每条路径当中有两个黑色结点:
c/d/e 子树每条路径当中有两个黑色结点的情况太多了,上图当中只是简单列出一些。
在 上述 只有一个黑结点的路径当中,只用一层就修改,就修改到了 cur 结点;而在当前 路径当中有两个黑结点,就是修改两层,才修改到 cur 结点的颜色的。(这里的层,一层就是 一个 cur parent grandfather 组合子树)
反正就是 路径当中有两个黑色结点的情况,要比 只有一个黑结点的情况复杂得多,但是最终还是属于情况一,都是使用 情况一的方式来进行解决。
情况二:
情况二当中的uncle有两种情况:
一种是 uncle不存在:

如果 uncle 不存在,那么 cur 一定是新插入的结点,因为如果 cur 不是新插入结点,那么 cur 和 p 当中一定至少有一个是 黑色的。
另一种是 uncle 的颜色是 黑色:

如果 uncle 是黑色的话,cur 这个结点一定不是 新插入的结点,因为,假设在插入之前,也就相当于是没有 cur 这个结点,g - > p -> null 路径 和 g -> u -> ········ 路径 两个路径上 黑色结点个数不一样。所以,插入之前的树不可能是红黑树。
所以,uncle 为黑的这种情况,一定是 cur 当中的子树发生了修改,往上修改的时候影响到了 cur :

修改过程如下:都是旋转 + 变色的方式。只不过旋转当中有四种方式,具体要看 cur parent grandfather 三者之间的链接关系。
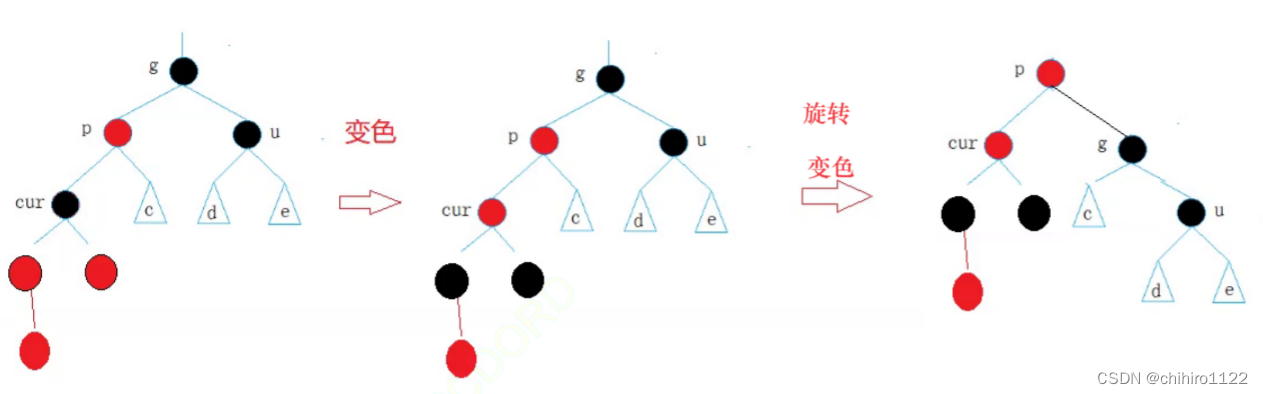
像上述这种情况, c 子树的路径当中每条之后一个黑结点,d 和 e 可能为空,也可能有一个 红结点。
同样的,c d e 三个子树当中的黑色结点可以按照上述的规律增加,那么就是不同的具体例子。
比如,c是 两个黑色结点的红黑树,那么 d 和 e 就是一个结点的红黑树。
红黑树的结果是无穷无尽的,每一种结构也相对复杂,但是上述都是属于 情况二,解决方式都是一样的。
- 情况二当中,旋转+变色之后,就不需要网上进行处理了,为在旋转+变色之后,这棵子树的根结点一定是 黑色的,不会是 红色的,那么黑色的结点不管和 红色的结点还是和 黑色的结点链接都是不会出现问题的。
- 在情况一当中之所以要继续往上更新,是因为,情况一修改出来的根结点是红色的。
红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
检测是否满足红黑树性质:
bool CheckColor(Node* root, int blacknum, int benchamark){// 当走到叶子结点的 null 指针处,也就是 NIL结点处if (root == nullptr){// 如果计算出的路径黑色结点长度 和 外部计算的不一样// 说明不是红黑树if (blacknum != benchamark){cout << "路径黑色结点个数不一样" << endl;return false;}return true;}// 用于递归计算 路径的黑色结点个数if (root->_color == BLACK)blacknum++;// 如果当前结点为 红色,且当前结点的父亲也是红色,就不是红黑树if (root->_parent && root->_parent->_color == RED && root->_color == RED){cout << "有连续红色" << endl;return false;}// 左右子树递归return CheckColor(root->_left, blacknum, benchamark)&& CheckColor(root->_right , blacknum, benchamark);}// 外部调用接口bool isBalance(){return isBalance(_root);}// 内部封装函数bool isBalance(Node* root){if (root == nullptr)return true;// 如果整棵树的 根结点不是 黑色的就不是红黑树if (root->_color != BLACK){cout << "根结点不是黑色" << endl;return false;}// 基准值// 在递归外部计算出左路第一条路径的 黑色结点值int benchmark = 0;Node* cur = root;while(cur){if (cur->_color == BLACK)benchmark++;cur = cur->_left;}return CheckColor(root, 0, benchmark);}我们使用两个函数相互调用来实现,外层函数判断整棵树的根结点是不是 黑色的;
而且计算左边第一条路径的黑色结点个数。其实可以随便找一条路径,因为这个只是一个基准值,不需要是正确的,因为红黑树当中的每一条路径都需要黑色结点数相同。
然后用内层函数递归遍历红黑树。
内层函数当中,计算出每一条黑色结点的个数;判断是否有连续的红色结点;
检测其是否满足二叉搜索树,就直接中序遍历打印就行了,这里就不实现了。
红黑树的删除
红黑树的删除和 AVL树一样,都比插入要复杂,可以看下面这个博客来了解:
红黑树 - _Never_ - 博客园 (cnblogs.com)
完整代码实现
#pragma once// 节点的颜色
enum Color { RED, BLACK };// 红黑树节点的定义
template<class K, class V>
struct RBTreeNode
{RBTreeNode(pair<K ,V> kv , Color color = RED): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _color(color){}RBTreeNode<K, V>* _left; // 节点的左孩子RBTreeNode<K, V>* _right; // 节点的右孩子RBTreeNode<K, V>* _parent; // 节点的双亲(红黑树需要旋转,为了实现简单给出该字段)pair<K, V> _kv; // 节点的值域Color _color; // 节点的颜色
};template<class K ,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public:bool insert(pair<K , V> kv){// 搜索二叉树的插入逻辑// // 如果当前树为空,直接用头指针只想新结点if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}// 不为空接着走Node* cur = _root; // 用于首次插入时候指针的迭代Node* parent = nullptr;while (cur){// 如果当前新插入的 key 值比 当前遍历的结点 key 值大if (cur->_kv.first < kv.first){// 往右迭代器parent = cur;cur = cur->_right;}// 反之else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{// 如果相等,就不插入,即插入失败return false;}}// 此时已经找到 应该插入的位置cur = new Node(kv);cur->_color = RED;// 再次判断大小,判断 cur应该插入到 parent 的那一边if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}// 链接 新插入结点 cur 的_parent 指针cur->_parent = parent;// 红黑树调整高度(平衡高度)的逻辑while (parent && parent->_color == RED){// parent 为 红,parent->_parent 一定不为空Node* grandfather = parent->_parent;// 如果父亲是在 祖父的左if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 叔叔存在且为红if (uncle && uncle->_color == RED){// 变色parent->_color = uncle->_color = BLACK;grandfather->_color = RED;// 向上迭代cur = grandfather;parent = cur->_parent;}// uncle 不存在 或者 存在且为黑else{if (cur == parent->_left){// g// p// cRotateR(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else // cur == parent->_right{// g// p// cRotateL(parent);RotateR(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break; // 不需要再往上更新}}else // parent = grandfather->_right{Node* uncle = grandfather->_left;// uncle 存在 且 uncle 的颜色是红色if (uncle && uncle->_color == RED){parent->_color = uncle->_color = BLACK;grandfather->_color = RED;cur = grandfather;parent = cur->_parent;}else // 不存在 或者 存在且为黑色{if (cur == parent->_right){// g// p// cRotateL(grandfather);parent->_color = BLACK;grandfather->_color = RED;}else // cur = parent->_left{// g// p// cRotateR(parent);RotateL(grandfather);cur->_color = BLACK;grandfather->_color = RED;}break; // 不用再往上更新}}}// 不管上述如何修改,红黑树的根结点永远是黑的// 所以我们这里既直接硬性处理_root->_color = BLACK;return true;}void RotateL(Node* parent){Node* cur = parent->_right; // 存储 parent 的右孩子Node* curleft = cur->_left; // 存储 cur 的左孩子parent->_right = curleft;if (curleft) // 判断 cur 的左孩子是否为空{curleft->_parent = parent; // 不为空就 修改 cur 的左孩子的_parent 指针}cur->_left = parent;// 留存一份 根结点指针Node* ppnode = parent->_parent;parent->_parent = cur;// 如果parent 是根结点if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){Node* cur = parent->_left;Node* curRight = cur->_right;parent->_left = curRight;if (curRight){curRight->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}bool CheckColor(Node* root, int blacknum, int benchamark){// 当走到叶子结点的 null 指针处,也就是 NIL结点处if (root == nullptr){// 如果计算出的路径黑色结点长度 和 外部计算的不一样// 说明不是红黑树if (blacknum != benchamark){cout << "路径黑色结点个数不一样" << endl;return false;}return true;}// 用于递归计算 路径的黑色结点个数if (root->_color == BLACK)blacknum++;// 如果当前结点为 红色,且当前结点的父亲也是红色,就不是红黑树if (root->_parent && root->_parent->_color == RED && root->_color == RED){cout << "有连续红色" << endl;return false;}// 左右子树递归return CheckColor(root->_left, blacknum, benchamark)&& CheckColor(root->_right , blacknum, benchamark);}// 外部调用接口bool isBalance(){return isBalance(_root);}// 内部封装函数bool isBalance(Node* root){if (root == nullptr)return true;// 如果整棵树的 根结点不是 黑色的就不是红黑树if (root->_color != BLACK){cout << "根结点不是黑色" << endl;return false;}// 基准值// 在递归外部计算出左路第一条路径的 黑色结点值int benchmark = 0;Node* cur = root;while(cur){if (cur->_color == BLACK)benchmark++;cur = cur->_left;}return CheckColor(root, 0, benchmark);}
private:Node* _root = nullptr;
};相关文章:

C++ - 红黑树 介绍 和 实现
前言 前面 学习了 AVL树,AVL树虽然在 查找方面始终拥有 O(log N )的极高效率,但是,AVL 树在插入 ,删除等等 修改的操作当中非常的麻烦,尤其是 删除操作,在实现当中细节非常多,在实现上非常难掌控…...

【蓝桥杯选拔赛真题62】Scratch判断小球 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch判断小球 一、题目要求 编程实现 二、案例分析 1、角色分析...

Spring面试题15:Spring支持几种bean的作用域?singleton、prototype、request的区别是什么?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:Spring支持几种bean的作用域? Spring支持以下几种Bean的作用域: Singleton(单例):这是Spring默认的作用域。使用@Scope(“singleton”)注解或…...

Spring Boot中Tomcat服务器参数解析及高并发控制
Spring Boot中Tomcat服务器参数解析及高并发控制 Spring Boot 集成了多种服务器,默认使用了Tomcat 服务器。在高并发情况下,合理地配置 Tomcat 服务器参数对于控制请求量和提高系统的稳定性至关重要。本文将解释 Spring Boot 中涉及 Tomcat 服务器的一些…...

Python 运行代码
一、Python运行代码 可以使用三种方式运行Python,如下: 1、交互式 通过命令行窗口进入 Python 并开始在交互式解释器中开始编写 Python 代码 2、命令行脚本 可以把代码放到文件中,通过python 文件名.py命令执行代码,如下ÿ…...
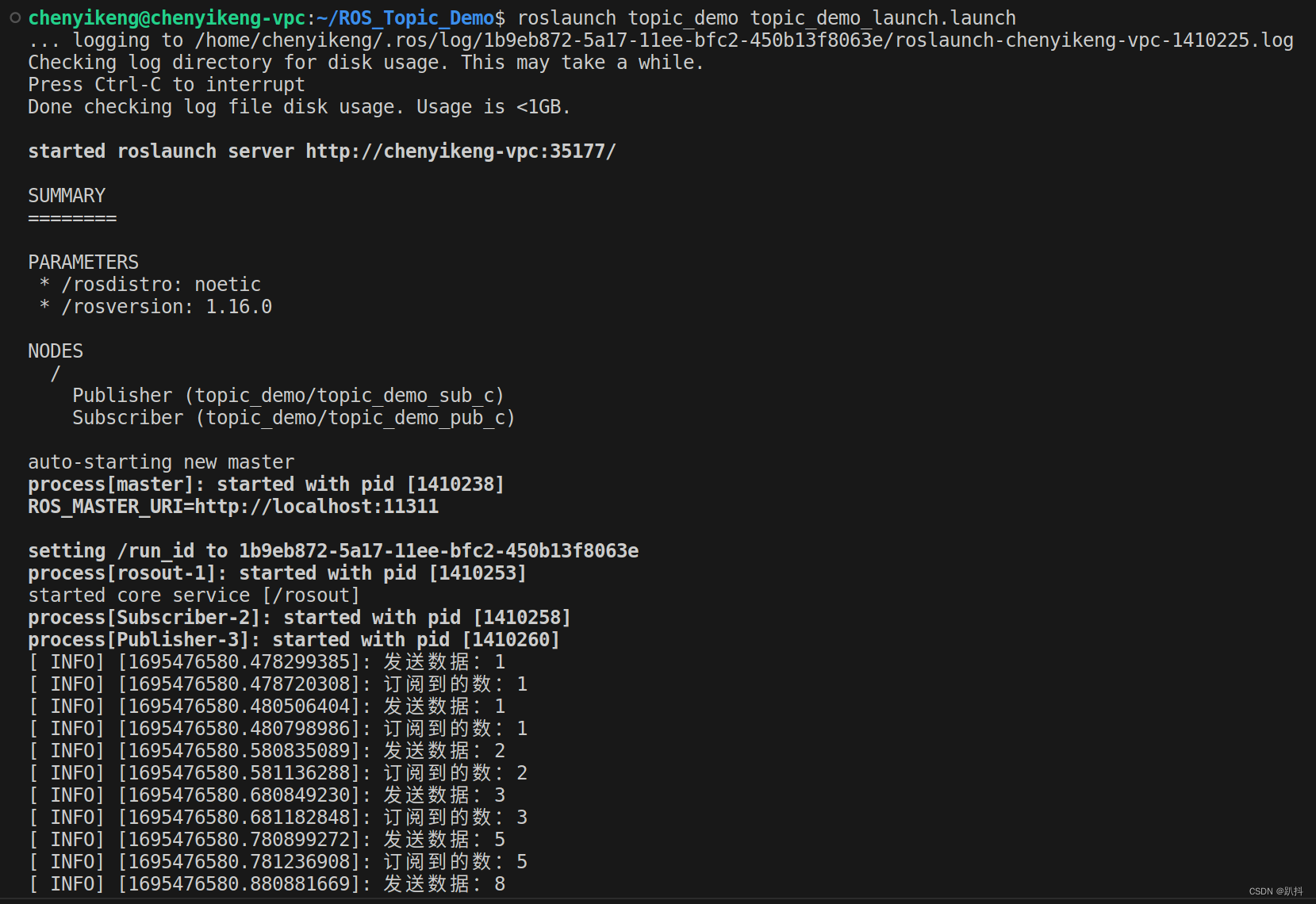
【ROS入门】使用 ROS 话题(Topic)机制实现消息发布与订阅及launch文件的封装
文章结构 任务要求话题模型实现步骤创建工作空间并初始化创建功能包并添加依赖创建发布者代码(C)创建订阅方代码(C)配置CMakeLists.txt执行启动roscore编译启动发布和订阅节点 launch封装执行 任务要求 使用 ROS 话题(Topic)机制…...
【企业级SpringBoot单体项目模板 】——Mybatis-plus自动代码生成
😜作 者:是江迪呀✒️本文关键词:SpringBoot项目模版、企业级、模版☀️每日 一言:我们之所以这样认为,是因为他们这样说。他们之所以那样说,是因为他们想让我们那样认为。所以实践才是检验真理…...
怒刷LeetCode的第14天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:动态规划 方法二:栈 方法三:双指针 第二题 题目来源 题目内容 解决方法 方法一:二分查找 方法二:线性扫描 方法三:递归 第三题 题目来源 …...
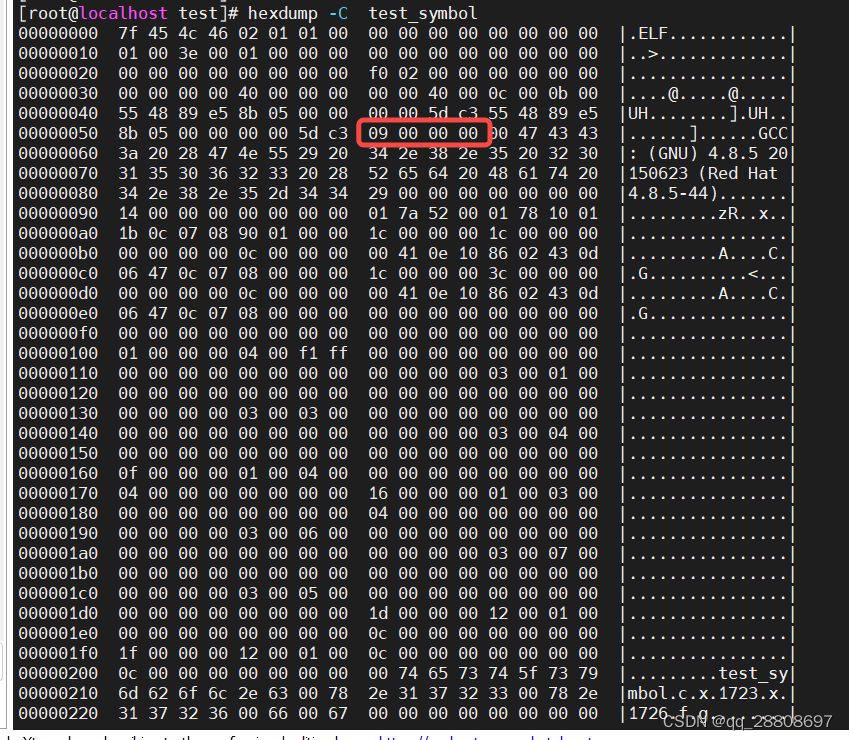
c语言 static
1、静态局部变量在程序加载时初始化,静态局部变量的初始值写入到了data段: 如下代码test_symbol.c int f() {static int x 0;return x; }int g() {static int x 9;return x; }使用命令gcc -c test_symbol.c -o test_symbol 编译 使用命令 readelf -a …...

java基础3
输入一个班学生的成绩,先显示所有及格的成绩,再显示所有不及格的成绩,最后显示及格人数和不及格人数 import java.util.Scanner; public class Hello{public static void main(String [] args) {int SIZE5;double grade[] new double[SIZE]…...
LeetCode 1194.锦标赛优胜者
数据准备 Create table If Not Exists Players (player_id int, group_id int); Create table If Not Exists Matches (match_id int, first_player int, second_player int, first_score int, second_score int); Truncate table Players; insert into Players (player_id, g…...
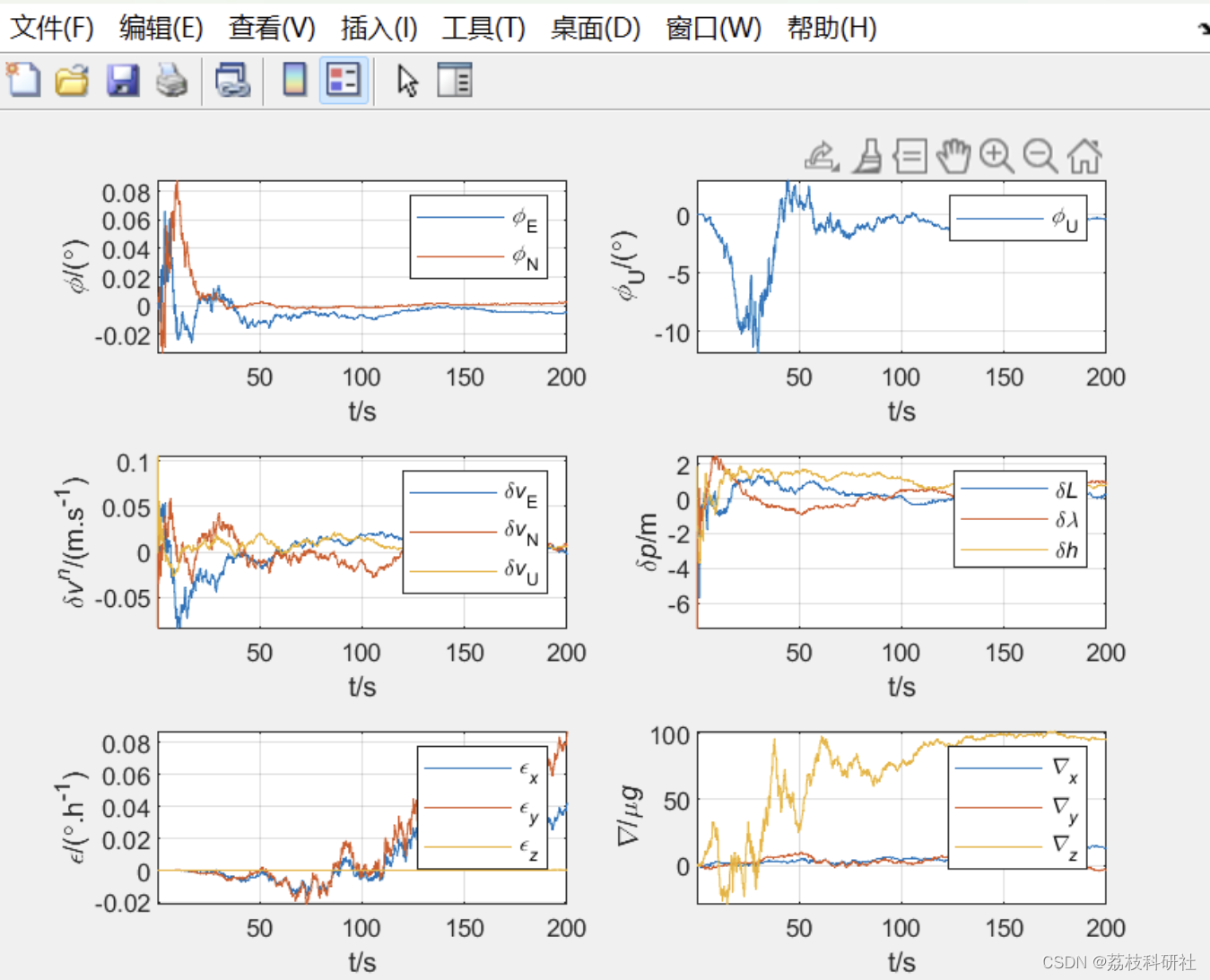
多旋翼无人机组合导航系统-多源信息融合算法(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

如何用ArkUI实现一个加入购物车效果?
关键词:ArkUI的动效能力,动效开发,ArkUI动画 我们在购买商品时,往往习惯将商品先加入购物车,然后在购物车里确认后再下订单,这是一个典型的访问者模式。对于这个高频场景,增添一些动效可以增加a…...
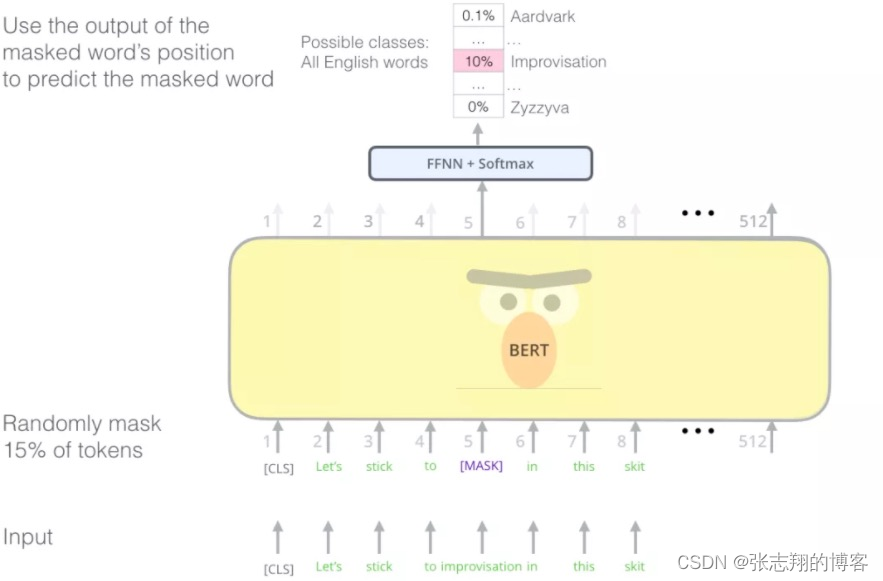
ChatGLM GPT原理介绍
图解GPT 除了BERT以外,另一个预训练模型GPT也给NLP领域带来了不少轰动,本节也对GPT做一个详细的讲解。 OpenAI提出的GPT-2模型(https://openai.com/blog/better-language-models/) 能够写出连贯并且高质量的文章,比之前语言模型效果好很多。GPT-2是基于Transformer搭建的,相…...
2015年蓝桥杯省赛C/C++ A组 灾后重建题解(100分)
10. 灾后重建 Pear市一共有N(<50000)个居民点,居民点之间有M(<200000)条双向道路相连。这些居民点两两之间都可以通过双向道路到达。这种情况一直持续到最近,一次严重的地震毁坏了全部M条道路。 震后…...
深分页Scroll)
Elasticsearch(四)深分页Scroll
一、前言 1.1、scroll与fromsize区别 ES对于fromsize的个数是有限制的,二者之和不能超过1w。当所请求的数据总量大于1w时,可用scroll来代替fromsize。 fromsize在ES查询数据的方式步骤如下: 1、先将用户指定的关键字进行分词;…...
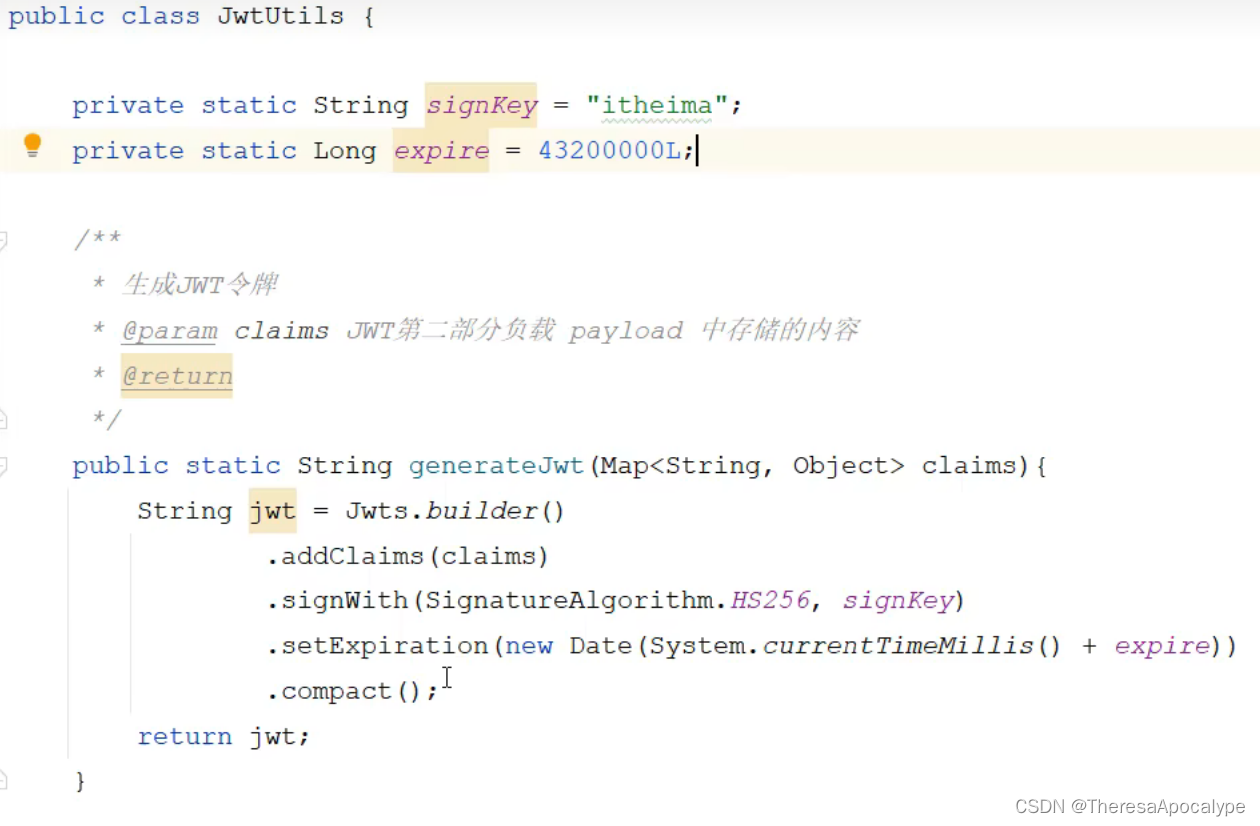
JavaWeb后端开发 JWT令牌解析 登录校验 通用模板/SpringBoot整合
目录 实现思路 会话跟踪的三个方案--引出Jwt令牌技术 1.访问cookie的值,在同一会话的不同请求之间共享数据 2.session 3.现代普遍采用的令牌技术--JWT令牌 JWT令牌技术 第一步--生成令牌 1.引入依赖 2.生成令牌 第二步--校验令牌 第三步--登录下发令牌 需要解决的…...

Sparta工具用法描述之信息收集(漏洞分析)
声明:本文仅做学习与交流,任何用于非法用途、行为等造成他人损失的,责任自负。本文不承担任何法律责任。 Sparta是python GUI应用程序,它通过在扫描和枚举阶段协助渗透测试仪来简化网络基础结构渗透测试。 通过点击并单击工具箱并以方便的方式显示所有工具输出,它可以使测…...

Vue复选框批量删除示例
Vue复选框批量删除 通过使用v-model指令绑定单个复选框 例如<input type"checkbox" id"checkbox" v-model"checked"> 而本次我们要做的示例大致是这样的,首先可以增加内容,然后通过勾选来进行单独或者批量删除&…...

Docker自定义镜像
一、镜像结构 镜像是将应用程序及其需要的系统函数库、环境、配置、依赖打包而成。 镜像是分层结构,每一层称为一个Layer BaseImage层:包含基本的系统函数库、环境变量、文件系统其它:在BaseImage基础上添加依赖、安装程序、完成整个应用的…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...