C语言结构体的一些鲜为人知的小秘密
目录
一、结构体内存对齐规则:
1.1范例
1.2结构体内存对齐规则
1.3自定义默认对齐数
二、位段
2.1什么是位段
2.2位段的内存分配
2.3位段的不足
三、枚举和联合体
3.1枚举
3.1.1枚举类型的定义
3.1.2枚举类型的使用
3.2联合体
3.2.1联合体的定义
3.2.2联合体的特点
一、结构体内存对齐规则:
1.1范例
我们来看一下结构体所占用的内存大小:
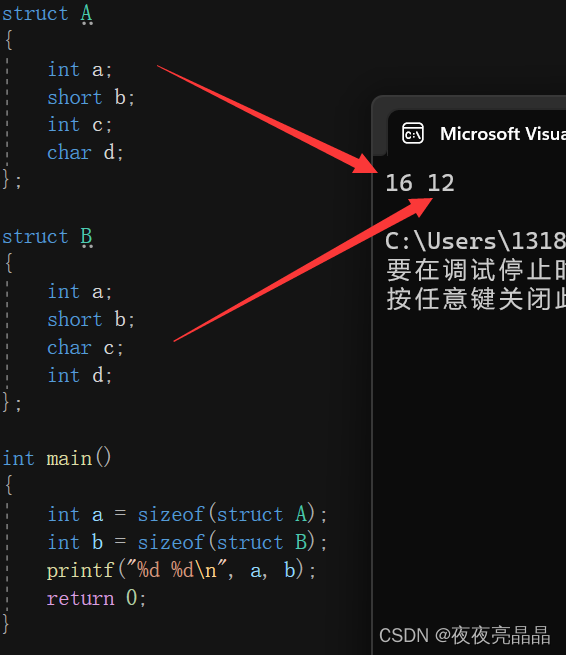
命名 A 和 B 的结构体成员都一样, 但是为什么他们占用的内存空间不一样呢?下面我们来介绍一下结构体内存的对齐规则。
1.2结构体内存对齐规则
首先我们要知道什么是对齐数,对齐数 = 编译器中默认的对齐数 与 该成员类型变量的大小(单位是byte)中的较小值。其中,VS默认的对齐数是8,Linux无默认对齐数,对齐数是其本身。
而在结构体中存放的数据,其地址并不是严格连续存放的,而是存放在其对齐数的整数倍。
编译器为结构体开创的大小,是最大对齐数的整数倍。
struct stu
{char name[20];int age;double grades;
};
int main()
{printf("%d\n", sizeof(struct stu));//结果为32return 0;
}

1.3自定义默认对齐数
之前在我们写三子棋时创建的 .h 文件中,我们就见过 #pragma 这个预处理指令,这里我们再次使用,可以改变我们的默认对齐数。

#pragma pack(8)//设置默认对齐数为8
struct A
{int a;short b;int c;char d;
};#pragma pack()//取消设置的默认对齐数,还原为默认
#pragma pack(1)//设置默认对齐数为1struct B
{int a;short b;char c;int d;
};
当我们把结构体 A 和 B 的默认对齐数都设置为1时,我们可以再次计算一下他们的大小

可以看出,他们的内存竟然都变成了11,这也说明了我们设置的默认对齐数起作用了。
二、位段
2.1什么是位段
很多朋友可能是第一次听说过位段,它是什么?为什么能和结构体扯上关系?
接下来我们对比一下位段类型的结构体和正常的结构体:

不难看出来,位段类型是在我们正常定义的变量基础上加上了 :数字 。其实这代表了我们定义的变量所需要占用的存储空间,单位是 bit 。
我们分别来计算上面两种结构体的大小,我们可以得出,使用位段的结构体只需要8字节,不使用位段的结构体却要16个字节。所以,位段是用来节省空间的。
2.2位段的内存分配
我们来看个例子了解在VS中位段的内存分配。
#include<stdio.h>struct _Record_Struct
{unsigned char Env_Alarm_ID : 4;unsigned char Para1 : 2;unsigned char state;unsigned char avail : 1;
};int main()
{sizeof(struct _Record_Struct);return 0;
}
 我们在VS中运行这个程序也可以得到结果是3(byte),和我们图中的一样。
我们在VS中运行这个程序也可以得到结果是3(byte),和我们图中的一样。
位段虽然能节省空间,但当两个位段类型超过 1byte 时,还是会浪费第一个位段类型剩余的几个 bit ,开辟下一个字节空间来存放第二个位段类型
我们再来看个例子来更直观的感受每一个 bit 位是怎么分配的。
struct S
{char a : 3;char b : 4;char c : 5;char d : 4;
};
int main()
{struct S s = { 0 };s.a = 10;s.b = 12;s.c = 3;s.d = 4;return 0;
}
接下来我们通过内存看一下他们存放的数据,每四个bit位在内存中对应一个十六进制数字:

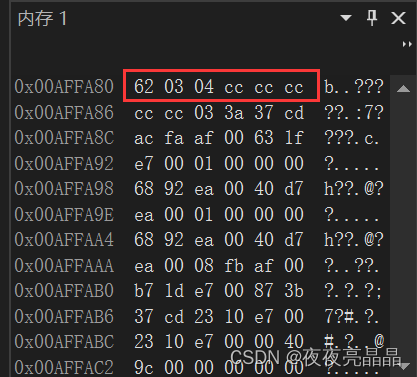
事实证明我们的理解是对的!
2.3位段的不足
我们上述只是讲解了VS中位段空间的分配,但是这仅仅是在VS中......
1. int 位段被当成有符号数还是无符号数是不确定的。
2. 位段中最大位的数目不能确定(16位机器最大16,32位机器最大32,写成27,在16位机器会出问题。)。
3. 位段中的成员在内存中从左向右分配,还是从右向左分配标准尚未定义。
4. 当一个结构包含两个位段,第二个位段成员比较大,无法容纳于第一个位段剩余的位时,是舍弃剩余的位还是利用,这是不确定的。
三、枚举和联合体
接下来我们介绍两种和结构体类似的自定义类型:枚举和联合体
3.1枚举
3.1.1枚举类型的定义
我们先来看一下枚举的语法:
enum Day//星期
{Mon,Tues,Wed,Thur,Fri,Sat,Sun
};enum + 命名,枚举中的类型用 , 隔开。
这些可能取值都是有值的,默认从0开始,一次递增1,当然在定义的时候也可以赋初值。赋初值后定义的类型取值从初值开始递增1,如:
enum Day
{Mon,//0Tues = 2,//2Wed,//3Thur,//4//......Fri,Sat,Sun
};3.1.2枚举类型的使用
枚举类型能怎么使用呢? 其实它的使用在我们写一些小应用时用到的概率大一点:
enum Day//星期
{Mon = 1,Tues,Wed,Thur,Fri,Sat,Sun
};int main()
{int input = 0;scanf("%d", &input);switch (input){case Mon:case Tues:case Wed:case Thur:case Fri:printf("今天是工作日\n"); break;case Sat:case Sun:printf("今天可以休息一下啦!\n"); break;}return 0;
}当我们用枚举常量代替 case 情况的取值时,我们的代码是不是变得清晰易懂?
枚举的优点:
1. 增加代码的可读性和可维护性
2. 和#define定义的标识符比较枚举有类型检查,更加严谨。
3. 防止了命名污染(封装)
4. 便于调试
5. 使用方便,一次可以定义多个常量
3.2联合体
3.2.1联合体的定义
联合也是一种特殊的自定义类型,这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间(所以联合也叫共用体)。
比如:
//联合类型的声明
union Un
{char c;int i;
};
//联合变量的定义
union Un un;
//计算连个变量的大小
printf("%d\n", sizeof(un));union + 命名,成员之间用 ; 相隔。
3.2.2联合体的特点
联合的成员是共用同一块内存空间的,这样一个联合变量的大小,至少是最大成员的大小(因为联合至少得有能力保存最大的那个成员)。
联合体占用空间也遵循结构体对齐规则。
相关文章:

C语言结构体的一些鲜为人知的小秘密
目录 一、结构体内存对齐规则: 1.1范例 1.2结构体内存对齐规则 1.3自定义默认对齐数 二、位段 2.1什么是位段 2.2位段的内存分配 2.3位段的不足 三、枚举和联合体 3.1枚举 3.1.1枚举类型的定义 3.1.2枚举类型的使用 3.2联合体 3.2.1联合体的定义 3.…...
-探究Pod被驱逐的原因及解决方法)
kubernetes问题(一)-探究Pod被驱逐的原因及解决方法
1 k8s evicted是什么 k8s evicted是Kubernetes中的一个组件,主要用于处理Pod驱逐的情况。在Kubernetes中,当Node节点资源不够用时,为了保证整个集群的运行稳定,会按照一定的优先级和策略将其中的Pod驱逐出去。这时就需要一个组件…...

论文速览【序列模型 seq2seq】—— 【Ptr-Net】Pointer Networks
标题:Pointer Networks文章链接:Pointer Networks参考代码(非官方):keon/pointer-networks发表:NIPS 2015领域:序列模型(RNN seq2seq)改进 / 深度学习解决组合优化问题【…...
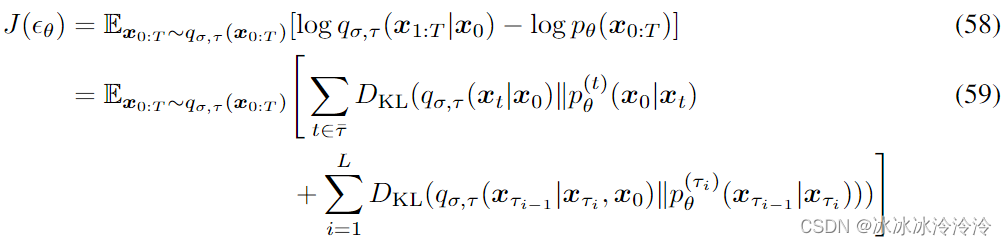
Denoising diffusion implicit models 阅读笔记
Denoising diffusion probabilistic models (DDPMs)从马尔科夫链中采样生成样本,需要迭代多次,速度较慢。Denoising diffusion implicit models (DDIMs)的提出是为了加速采样过程,减少迭代的次数,并且要求DDIM可以复用DDPM训练的网…...

【Java 基础篇】Executors工厂类详解
在多线程编程中,线程池是一项重要的工具,它可以有效地管理和控制线程的生命周期,提高程序的性能和可维护性。Java提供了java.util.concurrent包来支持线程池的创建和管理,而Executors工厂类是其中的一部分,它提供了一些…...

SpringBoot MongoDB操作封装
1.引入Jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId></dependency> 2.MongoDbHelper操作 /*** MongoDB Operation class* author Mr.Li* date 2022-12-05*…...

PyTorch 模型性能分析和优化 — 第 1 部分
一、说明 这篇文章的重点将是GPU上的PyTorch培训。更具体地说,我们将专注于 PyTorch 的内置性能分析器 PyTorch Profiler,以及查看其结果的方法之一,即 PyTorch Profiler TensorBoard 插件。 二、深度框架 训练深度学习模型,尤其是…...

Unity3D 简易音频管理器
依赖于Addressable 依赖于单例模板:传送门 using System.Collections.Generic; using System.Security.Cryptography; using System; using UnityEngine; using UnityEngine.AddressableAssets;namespace EasyAVG {public class AudioManager : MonoSingleton<…...

【李沐深度学习笔记】线性回归
课程地址和说明 线性回归p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性回归 如何在美国买房(经典买房预测问题) 一个简化的模型 线性模型 其中, x → [ x 1 , x 2 ,…...
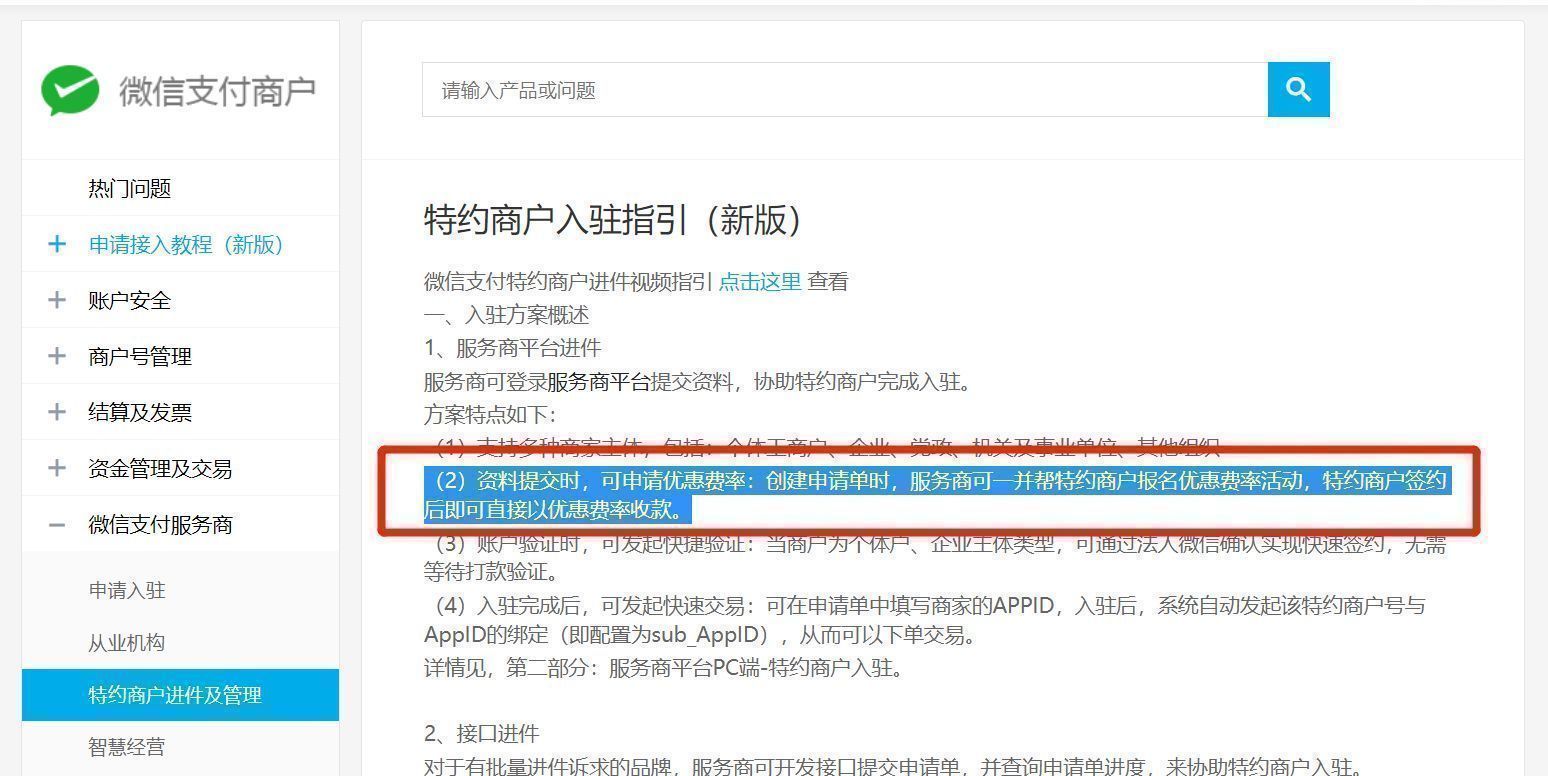
微信收款码费率0.38太坑了
作为一个有多年运营经验的商家,我本人在申请收款功能时曾经走过了不少弯路。我找遍了市面上的知名的支付公司,但了解到的收款手续费率通常都在0.6左右,最低也只能降到0.38。这个过程吃过不少苦头。毕竟,收款功能是我们商家的命脉&…...

【学习笔记】CF1103D Professional layer
首先分析不出啥性质,所以肯定是暴力优化😅 常见的暴力优化手段有均摊,剪枝,数据范围分治(points),答案值域分析之类的。 比较经典的题目是 CF1870E Another MEX Problem,可以用剪枝…...

vue之Pinia
定义 Store | Pinia 开发文档 1.什么是Pinaia Pinia 是 Vue 的专属状态管理库,它允许你跨组件或页面共享状态。 2.理解Pinaia核心概念 定义Store 在深入研究核心概念之前,我们得知道 Store 是用 defineStore() 定义的,它的第一个参数要求是一…...
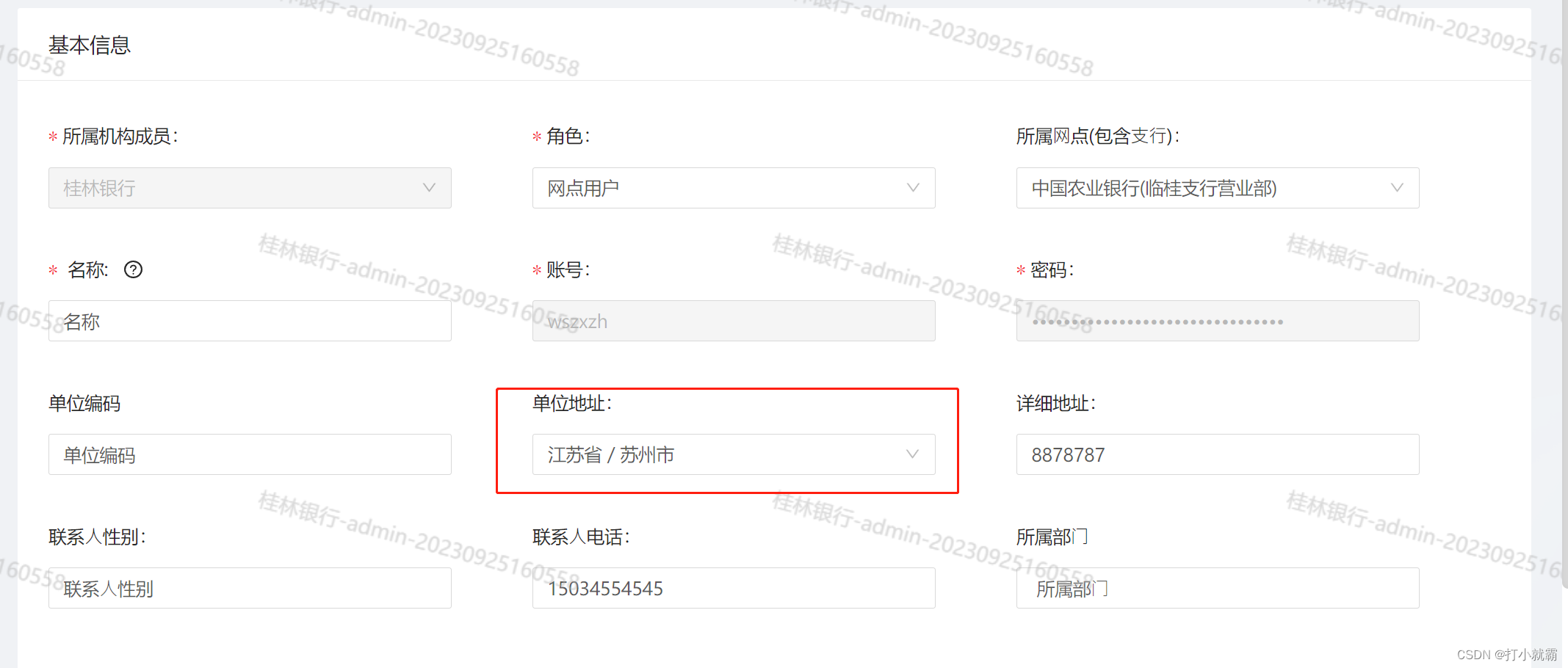
antd-vue 级联选择器默认值不生效解决方案
一、业务场景: 最近在使用Vue框架和antd-vue组件库的时候,发现在做编辑回显时** 级联选择器** 组件的默认值不生效。为了大家后面遇到和我一样的问题,给大家分享一下 二、bug信息: 三、问题原因: 确定不了唯一的值&a…...
分享53个Python源码源代码总有一个是你想要的
分享53个Python源码源代码总有一个是你想要的 链接:https://pan.baidu.com/s/1ew3w2_DXlSBrK7Mybx3Ttg?pwd8888 提取码:8888 项目名称 100-Python ControlXiaomiDevices DRF-ADMIN 后台管理系统 FishC-Python3小甲鱼 Flask框架的api项目脚手架 …...
【每日一题】658. 找到 K 个最接近的元素
658. 找到 K 个最接近的元素 - 力扣(LeetCode) 给定一个 排序好 的数组 arr ,两个整数 k 和 x ,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。 整数 a 比整数 b 更接近 …...
)
并发任务队列(字节青训测试题)
需求描述 封装一个并发任务队列类,用于对一些异步任务按指定的并发数量进行并发执行。 /*** 延迟函数* param {number} time - 延迟时间* return {Promise} delayFn - 延迟函数(异步封装)*/ function timeout(time) {return new Promise((resolve) > {setTimeo…...
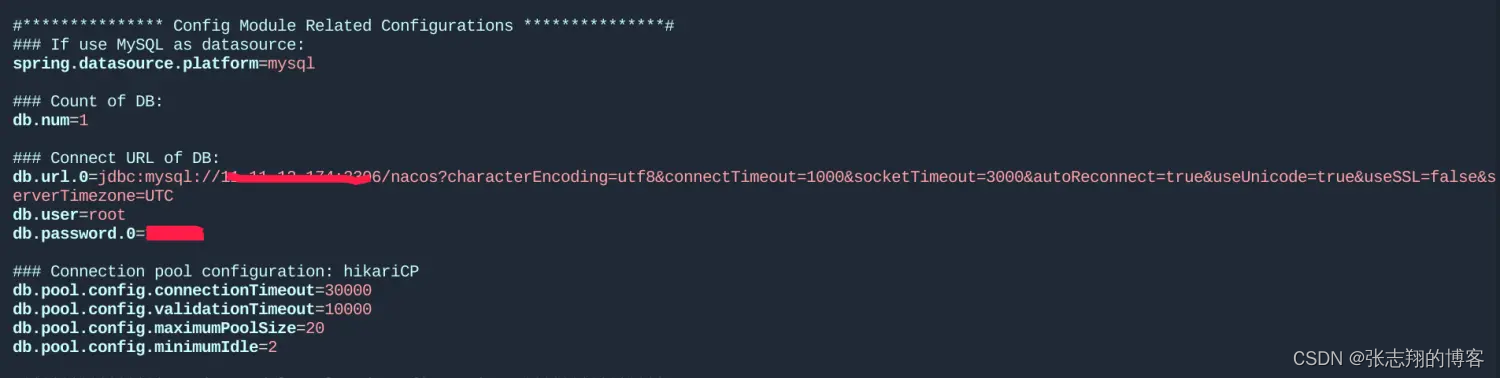
Ubuntu 安装Nacos
1、官网下载最新版nacos https://github.com/alibaba/nacos/releases 本人环境JDK8,Maven3.6.3,启动Nacos2.2.1启动失败,故切换到2.1.0启动成功 2、放到服务器目录下,我的在/home/xxx/apps下 3、解压 $ tar -zxvf nacos-serve…...

CSS 小球随着椭圆移动
html代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><…...
【李沐深度学习笔记】线性代数
课程地址和说明 线性代数p1 本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。 线性代数 标量 标量(scalar),亦称“无向量”。有些物理量,只具有数值大小,…...

vuejs - - - - - 递归组件的实现
递归组件的实现 1. 需求描述:2. 效果图:3. 代码3.1 封装组件代码3.2 父组件使用 1. 需求描述: 点击添加行,增加一级目录结构当类型为object or array时,点击右侧➕,增加子集点击右侧🚮&#x…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
