了解”变分下界“
“变分下界”:在变分推断中,我们试图找到一个近似概率分布q(x)来逼近真实的概率分布p(x)。变分下界是一种用于评估近似概率分布质量的指标,通常用来求解最优的近似分布。它的计算涉及到对概率分布的积分或期望的估计

相关文章:

了解”变分下界“
“变分下界”:在变分推断中,我们试图找到一个近似概率分布q(x)来逼近真实的概率分布p(x)。变分下界是一种用于评估近似概率分布质量的指标,通常用来求解最优的近似分布。它的计算涉及到对概率分布的积分或期望的估计...

Andriod 简单控件
目录 一、文本显示1.1 设置文本内容1.2 设置文本大小1.3 设置文本颜色 二、视图基础2.1 设置视图宽高2.2 设置视图间距2.3 设置视图对齐方式 三、常用布局3.1 线性布局LinearLayout3.2 相对布局RelativeLayout3.3 网格布局GridLayout3.4 滚动视图ScrollView 四、按钮触控4.1 按…...

Substructure‑aware subgraph reasoning for inductive relation prediction
摘要 关系预测的目的是推断知识图中实体之间缺失的关系,其中归纳关系预测因其适用于新兴实体的有效性而广受欢迎。大多数现有方法学习逻辑组合规则或利用子图来预测缺失关系。尽管在性能方面已经取得了很大的进展,但目前的模型仍然不是最优的,因为它们捕获拓扑信息的能力有…...

古诗词学习鉴赏APP设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

深度学习与python theano
文章目录 前言1.人工神经网络2.计算机神经网络3.反向传播4.梯度下降-cost 函数1.一维2.二维3.局部最优4.迁移学习 5. theano-GPU-CPU theano介绍1.安装2.基本用法1.回归2.分类 3.function用法4.shared 变量5.activation function6.Layer层7.regression 回归例子8.classificatio…...
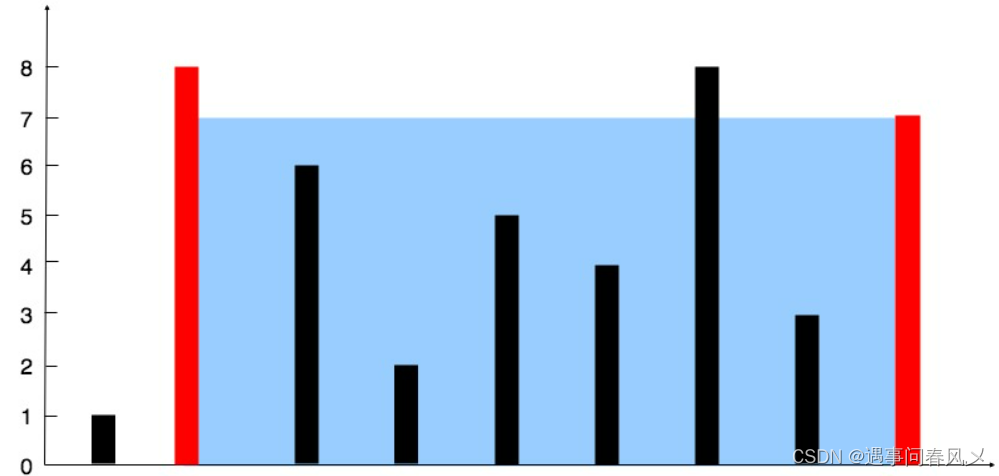
【算法优选】双指针专题——贰
文章目录 😎前言🌲[快乐数](https://leetcode.cn/problems/happy-number/)🚩题目描述🚩题⽬分析:🚩算法思路:🚩代码实现: 🎋[盛水最多的容器](https://leetco…...

AI智能电话机器人实用吗
近几年,人工智能得到很大的发展,同时语音识别技术的不断完善,很多以语音识别为基础的应用涌现出来,尤其是最近3年,出现了很多智能电话机器人。百度开发者大会上展示了百度智能客服也吸引了很多人对智能电话机器人的兴趣…...
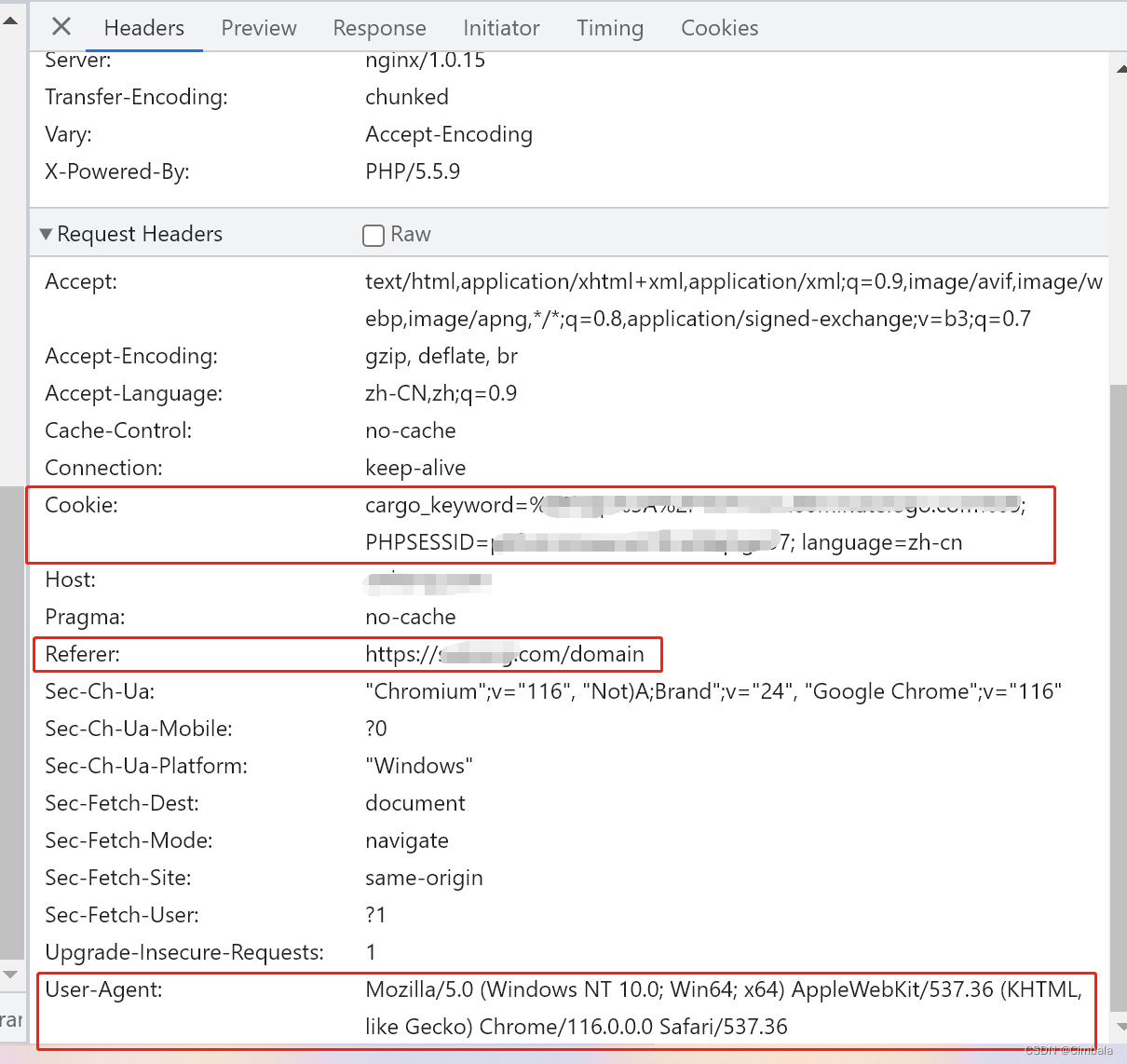
网络爬虫--伪装浏览器
从用户请求的Headers反反爬 在访问某些网站的时候,网站通常会用判断访问是否带有头文件来鉴别该访问是否为爬虫,用来作为反爬取的一种策略。很多网站都会对Headers的User-Agent进行检测,还有一部分网站会对Referer进行检测(一些资…...
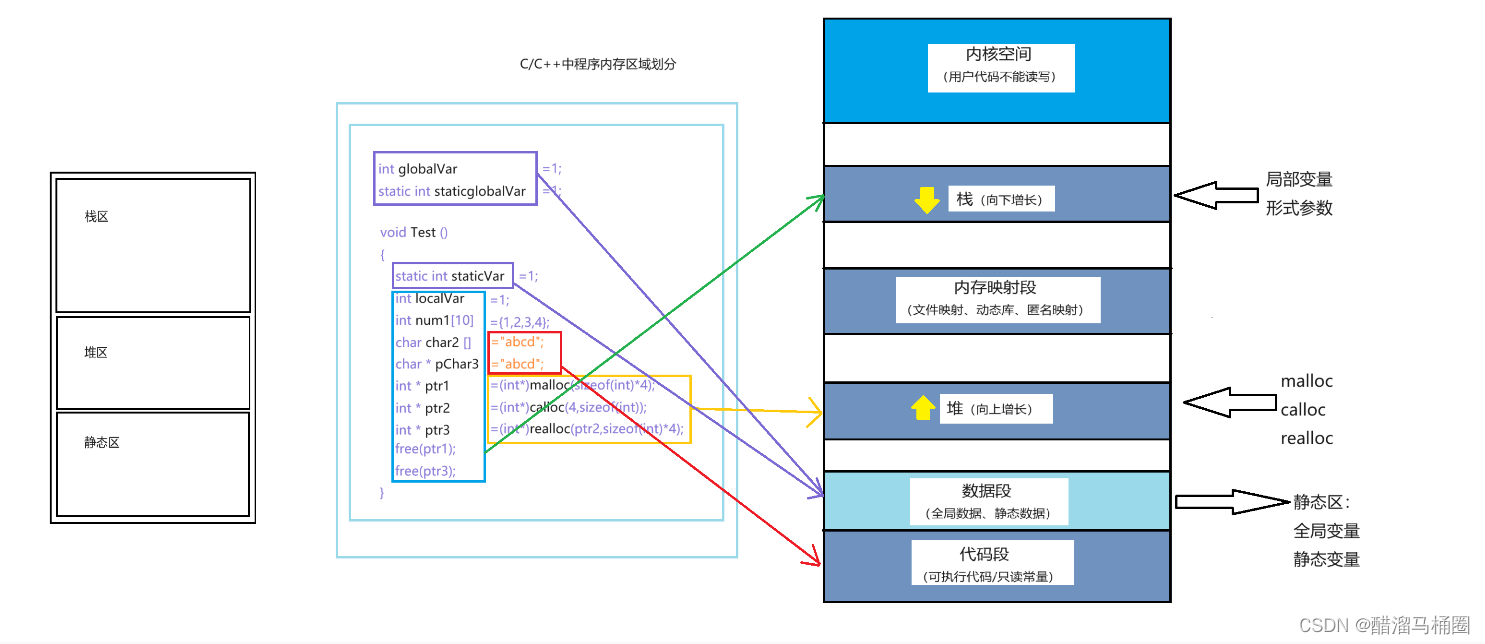
C/C++程序的内存开辟
前面我们说过,计算机中内存分为三个区域:栈区,堆区,静态区 但是这只是个简化的版本,接下来我们仔细看看内存区域的划分 C/C程序内存分配的几个区域: 栈区(stack):在执行…...

【Java 进阶篇】JDBC DriverManager 详解
JDBC(Java Database Connectivity)是 Java 标准库中用于与数据库进行交互的 API。它允许 Java 应用程序连接到各种不同的数据库管理系统(DBMS),执行 SQL 查询和更新操作,以及处理数据库事务。在 JDBC 中&am…...

2023年Linux总结常用命令
1.常用命令 1.1创建文件夹 mkdir -p forever/my 1.2当前目录 pwd 1.3创建文件 touch 1.txt 1.4查看文件 cat 1.txt 1.5复制文件 说明:-r是复制文件夹 cp -r my myCopy 1.6删除文件 说明:-r带包删除文件夹,-f表示强制删除(保存问题) rm -r…...
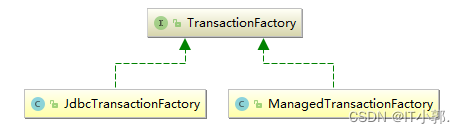
Mybatis3详解 之 全局配置文件详解
1、全局配置文件 前面我们看到的Mybatis全局文件并没有全部列举出来,所以这一章我们来详细的介绍一遍,Mybatis的全局配置文件并不是很复杂,它的所有元素和代码如下所示: <?xml version"1.0" encoding"UTF-8&…...

力扣-345.反转字符串中的元音字母
Idea 将s中的元音字母存在字符串sv中,并且使用一个数组依次存储元音字母的下标。 然后将字符串sv进行反转,并遍历元音下标数组,将反转后的字符串sv依次插入到源字符串s中 AC Code class Solution { public:string reverseVowels(string s) {…...

643. 子数组最大平均数I(滑动窗口)
目录 一、题目 二、代码 一、题目 643. 子数组最大平均数 I - 力扣(LeetCode) 二、代码 class Solution { public:double findMaxAverage(vector<int>& nums, int k) {double Average INT_MIN;double sum nums[0];int left 0, right 0…...

Java 21 新特性:虚拟线程(Virtual Threads)
I often take exercise. Why only yesterday I had breakfast in bed. 在Java 21中,引入了虚拟线程(Virtual Threads)来简化和增强并发性,这使得在Java中编程并发程序更容易、更高效。 虚拟线程,也称为“用户模式线程…...

18scala笔记
Scala2.12 视频地址 1 入门 1.1 发展历史 … 1.2 Scala 和 Java Scala Java 编写代码使用scalac编译成.class字节码文件scala .class文件 执行代码 1.3 特点 1.4 安装 视频地址 注意配置好环境变量 简单代码 1.5 编译文件 编译scala文件会产生两个.class文件 使用java…...

【LeetCode周赛】LeetCode第365场周赛
目录 有序三元组中的最大值 I有序三元组中的最大值 II无限数组的最短子数组 有序三元组中的最大值 I 给你一个下标从 0 开始的整数数组nums。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的…...
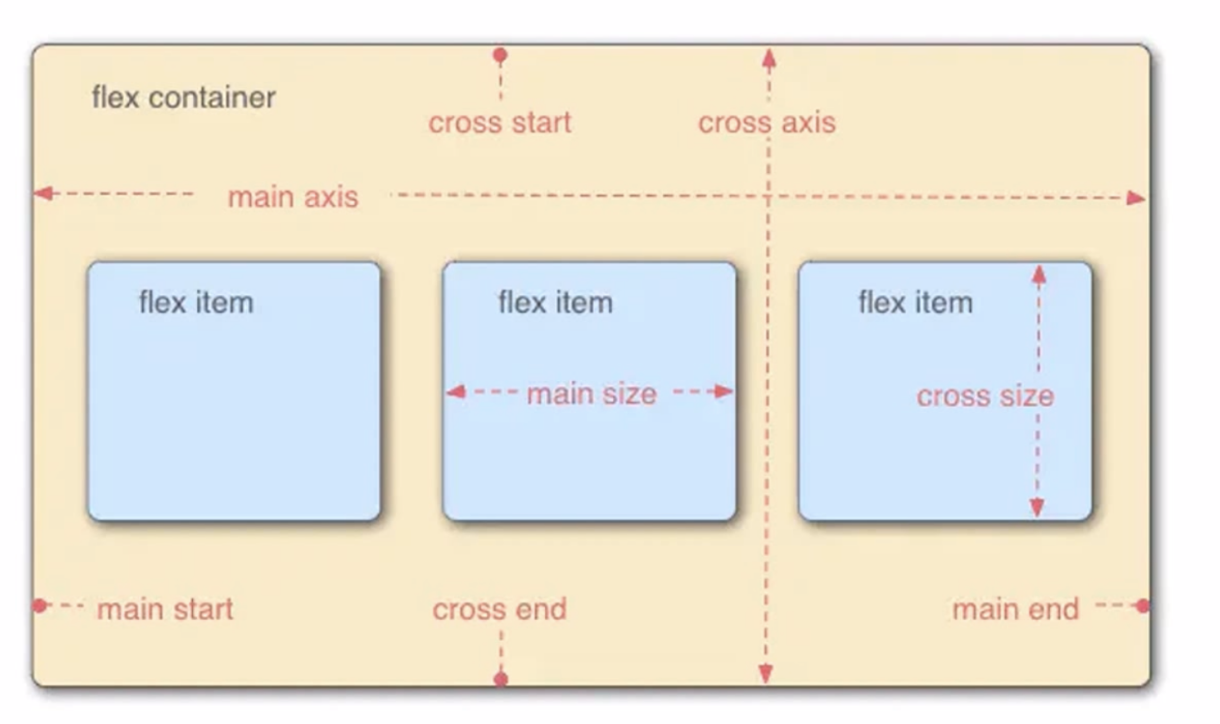
响应式设计的实现方式
一. 什么是响应式 响应式网站设计是一种网络页面设计布局。页面的设计与开发应当根据用户行为以及设备环境(系统平台,屏幕尺寸,屏幕定向等)进行相应的响应和调整。 响应式网站常见特点: 1. 同时适配PC平板手机。 2…...

PHP 反序列化漏洞:__PHP_Incomplete_Class 与 serialize(unserialize($x)) !== $x;
文章目录 参考环境声明__PHP_Incomplete_Class灵显为什么需要 __PHP_Incomplete_Class?不可访问的属性 serialize(unserialize($x)) $x;serialize(unserialize($x)) ! $x;雾现__PHP_Incomplete_Class 对象与其序列化文本的差异试构造 __PHP__Incomplete_Class 对象…...

TempleteMethod
TempleteMethod 动机 在软件构建过程中,对于某一项任务,它常常有稳定的整体操作结构,但各个子步骤却有很多改变的需求,或者由于固有的原因 (比如框架与应用之间的关系)而无法和任务的整体结构同时实现。如…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
