程序在线报刊第一期

文章目录
- 程序在线报刊第一期
- 排序算法:优化数据处理效率的核心技术
- 回顾区块链技术:去中心化引领数字经济新时代
- 展望AI未来:智能化时代的无限可能
程序在线报刊第一期
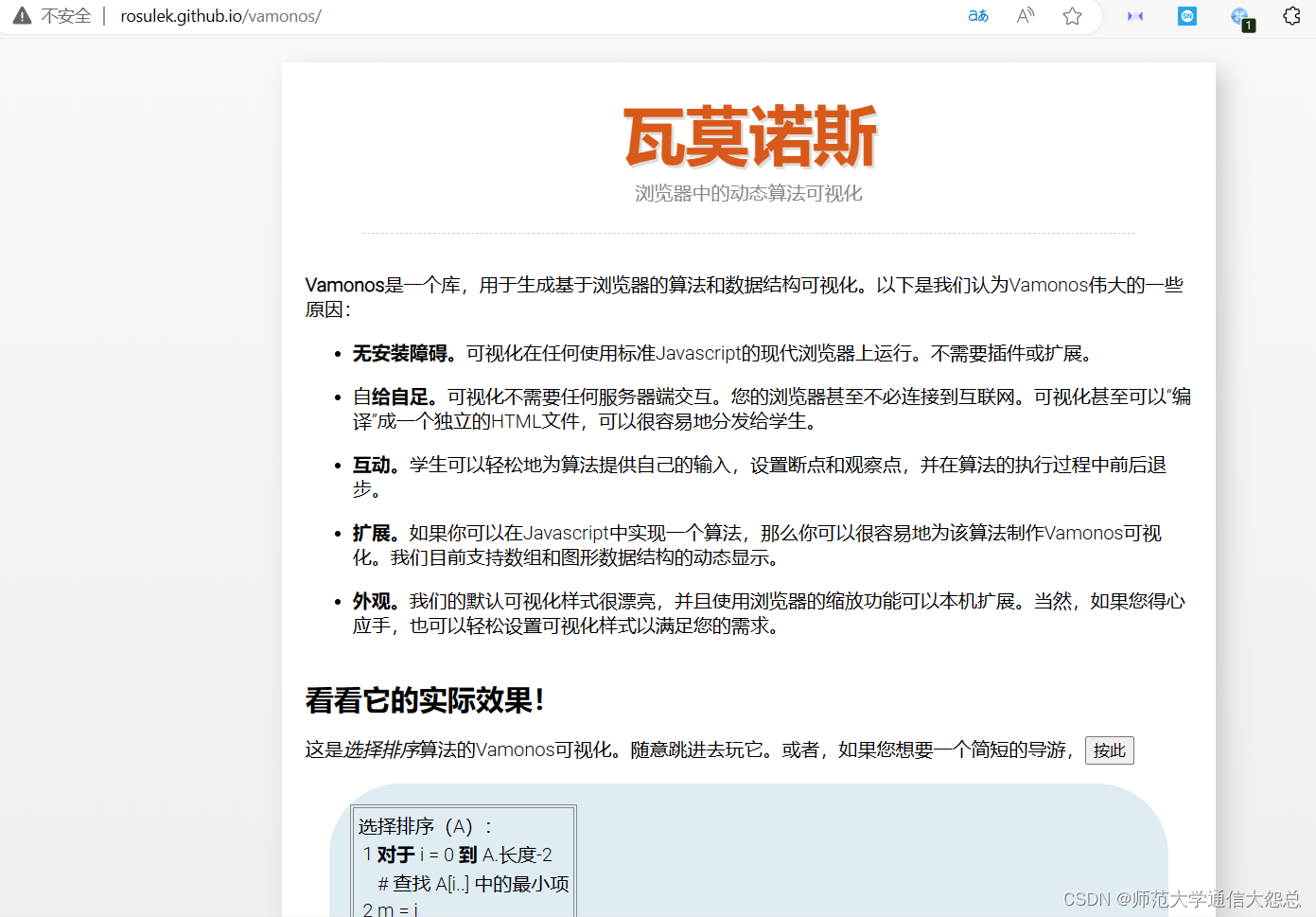
排序算法:优化数据处理效率的核心技术
近年来,随着大数据和人工智能技术的快速发展,对于高效处理大规模数据的需求也日益迫切。在这个背景下,排序算法作为数据处理的核心技术之一,受到了越来越多的关注和广泛应用。
排序算法是一种通过对数据进行排序,使其按照一定顺序排列的算法。它在众多领域都有广泛的应用,如搜索引擎、数据库管理、数据压缩等。通过排序算法,可以更快速地查找、插入、删除和合并大量数据,从而提高数据处理的效率和准确性。
在排序算法中,冒泡排序、插入排序、选择排序和快速排序是常见且经典的几种算法。冒泡排序通过依次比较和交换相邻元素的方式,将最大(小)的元素逐渐“冒泡”到序列的末尾,实现排序。插入排序则通过构建一个有序序列,逐步将未排序元素插入到有序序列的合适位置,最终完成排序。选择排序通过每次选择最小(大)的元素,并将其放到已排序序列的末尾,逐步形成有序序列。快速排序则是基于“分治”的思想,通过将一个序列分为较小和较大两个子序列,递归地对子序列进行排序,最终完成整个序列的排序。
这些排序算法各有特点,适用于不同规模和类型的数据。冒泡排序简单直观,对于元素个数较少的情况下效果不错;插入排序在数据近乎有序的情况下性能很好;选择排序虽然效率较低,但在某些特定场景下仍有用武之地;而快速排序则是最常用和高效的排序算法之一,其时间复杂度为O(nlogn),适用于各种数据规模。
随着数据量的不断增大,优化排序算法的性能变得尤为重要。研究者们也在不断努力,提出了各种改进和优化的算法,如归并排序、堆排序、计数排序等。这些算法在特定条件下能够更好地提高排序效率,满足现代大数据处理的需求。
未来,随着技术的进一步发展和应用场景的拓展,排序算法仍将处于不断演进和完善的过程中。我们可以期待,通过不断优化和创新,排序算法将为数据处理领域带来更多惊喜与突破,推动着我们走向更加智能化和高效化的时代。
回顾区块链技术:去中心化引领数字经济新时代
随着数字经济的蓬勃发展,区块链技术作为一项革命性的创新技术逐渐崭露头角,引起了全球范围内的浓厚关注。作为一种去中心化的分布式账本技术,区块链以其独特的安全性、透明性和可扩展性,为数字经济注入了新的活力。
区块链技术最初是随着比特币的出现而引起广泛瞩目的。比特币是由中本聪在2008年提出的一种去中心化的数字货币,区块链技术则是为了保障比特币的安全性而诞生的。通过将交易记录以区块的形式进行链式连接,并采用密码学算法保证安全性,比特币成为了首个成功应用区块链技术的案例。随着比特币的成功,人们开始意识到,区块链技术具有广阔的应用前景,不仅可以应用于金融领域,还能够应用于供应链管理、物联网、知识产权保护等领域。
区块链技术的核心特点是去中心化和不可篡改性。传统的中心化系统需要依赖中心服务器来进行数据存储和交易验证,而区块链技术通过分布在网络节点上的共识机制,将数据存储和验证的权力下放到网络的每一个参与者手中,实现了去中心化。同时,区块链中的数据以区块的形式进行链式连接,每一个区块都包含了前一个区块的哈希值,使得数据不可随意更改,确保了数据的不可篡改性和安全性。
除了在金融领域的应用,区块链技术也被广泛探索和应用于其他行业。在供应链管理中,区块链技术可以提供真实、可追溯的供应链信息,帮助降低欺诈风险和提高生产者和消费者之间的信任度。在物联网领域,区块链技术可以实现设备之间的可信交互和数据共享,促进物联网生态的发展。在知识产权保护方面,区块链技术可以提供不可篡改的存证和交易记录,保护作者的权益。
然而,随着区块链技术的发展和应用,也暴露出一些问题和挑战。例如,性能和扩展性问题、隐私和安全问题等。为了更好地推动区块链技术的发展,各界正在积极探索解决方案,包括共识机制的优化、隐私保护技术的研究等。
回顾区块链技术的发展历程,我们不难发现,它已经在数字经济领域展现出了巨大的潜力和影响力。未来,随着技术的不断成熟和应用场景的不断扩展,区块链技术将继续为数字经济注入新的动力,推动着我们迈向数字经济新时代的进程。我们有理由相信,区块链技术将成为推动经济发展和社会进步的重要力量,为人类创造更美好的未来。
展望AI未来:智能化时代的无限可能
人工智能(Artificial Intelligence,简称AI)作为当今科技领域最为炙手可热的技术之一,正引领着人类走向智能化时代。随着技术的不断成熟和应用的广泛拓展,AI未来的发展前景令人充满期待。
近年来,AI技术在各个领域都取得了突破性的进展。在医疗领域,AI技术能够辅助医生进行疾病诊断、药物研发和患者健康管理,提高医疗效率和准确性。在交通领域,AI技术的应用使得智能驾驶、交通管控等变得可能,为人们带来更安全、高效的出行方式。在工业领域,AI技术能够实现智能制造、机器人协作等,提高生产效率和品质。
然而,AI的发展仍然面临着一些挑战。一个重要的挑战是技术瓶颈,尤其是在复杂环境下的智能决策和推理能力。另外,数据隐私和伦理道德问题也引起了广泛关注。解决这些问题需要跨学科的合作和持续的创新。
展望AI未来,我们可以看到许多令人激动的发展趋势。首先,AI将进一步走向普及和深度融合。它将渗透到日常生活的方方面面,为人们提供更个性化、智能化的服务和体验。其次,AI与其他技术的融合将会加速创新。例如,结合大数据、云计算和物联网技术,AI将带来更多智能化的解决方案,如智慧城市、智能家居等。再次,AI赋能创新将推动新兴产业的崛起。通过AI技术的应用,新的商业模式和产业生态将逐渐形成,为经济增长注入新的动力。
为了实现AI未来的发展愿景,社会各界需要共同努力。政府部门需要加大对AI产业的支持,制定相关政策和法规,为AI技术的研发、应用和推广创造有利环境。企业需要加强研发力量,加大对AI技术的投入,与科研机构、高校等加强合作,推动AI技术的创新和商业化。同时,加强对技术伦理和数据隐私的保护,确保AI的发展符合社会价值和道德规范。
展望AI未来,我们正站在一个充满无限可能的时代。AI技术将持续演进和进步,为人类带来更多便利、高效和智能化的生活方式。让我们共同期待,为AI的未来携手努力,共同创造一个更加智慧、美好的世界。
相关文章:

程序在线报刊第一期
文章目录 程序在线报刊第一期排序算法:优化数据处理效率的核心技术回顾区块链技术:去中心化引领数字经济新时代展望AI未来:智能化时代的无限可能 程序在线报刊第一期 排序算法:优化数据处理效率的核心技术 近年来,随…...

k8s 拉取镜像报错 no basic auth credentials
文章目录 [toc]基于现有凭据创建 Secret通过命令行创建 Secretpod 使用指定 secret 认证私有镜像仓库 省流提醒: 本次解决的问题是 docker login 可以正常登录,docker pull 也可以正常拉取镜像,只是 k8s 在启动 pod 的时候,没有指…...
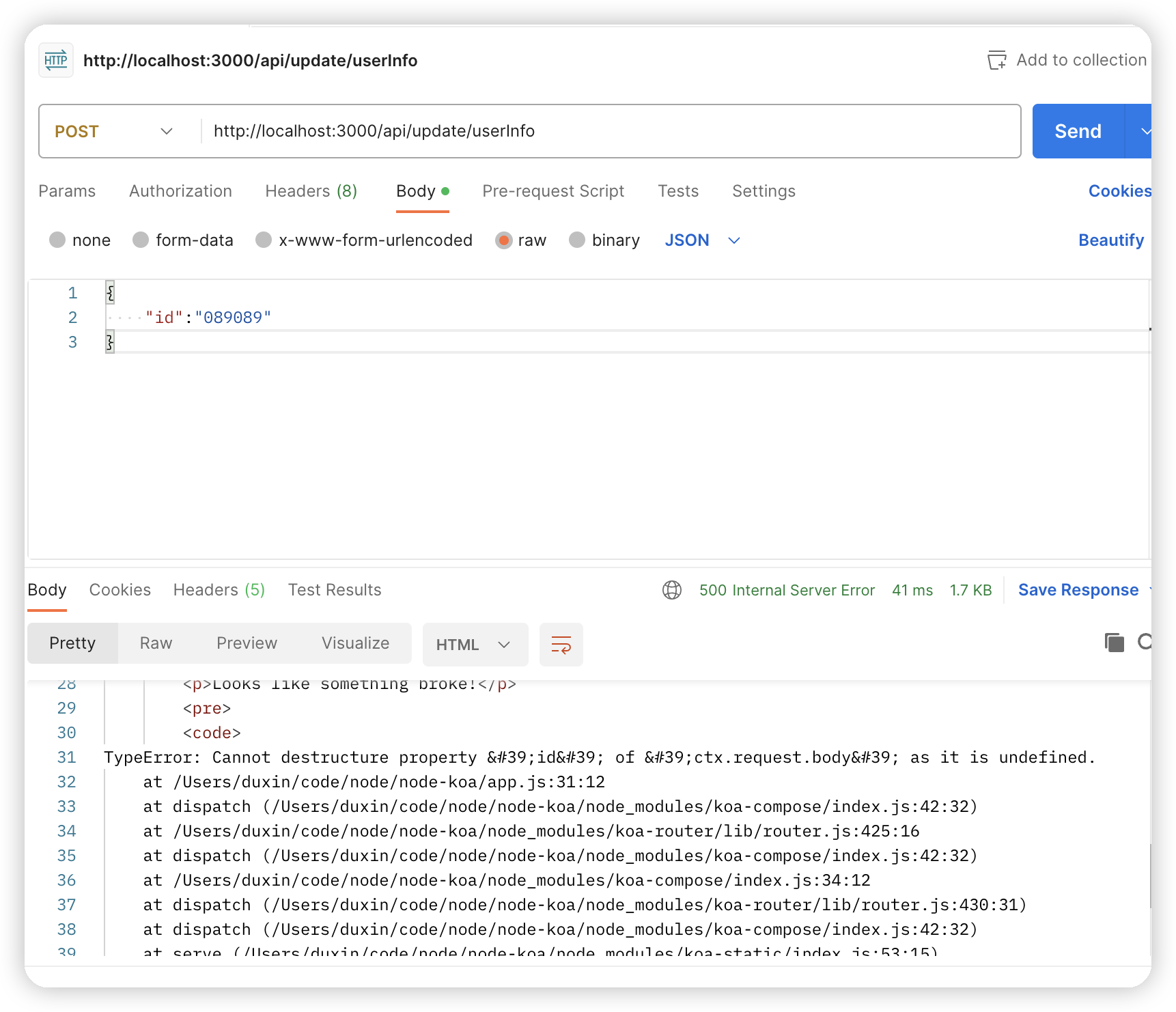
Koa处理请求数据
在开发中,后端接收到请求参数后,需要解析参数。请求分为很多种类型,比如常见的get和post。 请求参数 Koa本身可以解析get请求参数,不能解析post请求参数。例如: router.get(/api/get/userInfo, async (context) >…...

关于浮点数的 fld、fadd、fstp 汇编指令介绍
文章目录 FLDFADDFSTP FLD, FADD 和 FSTP 常在一起出现,用于 float 运算。组合实现浮点数的加载、加法运算和保存 FLD FLD 指令用于将 浮点数 从内存加载到浮点寄存器栈(FPU Stack)中。它的使用方式如下: FLD <源内存地址&g…...
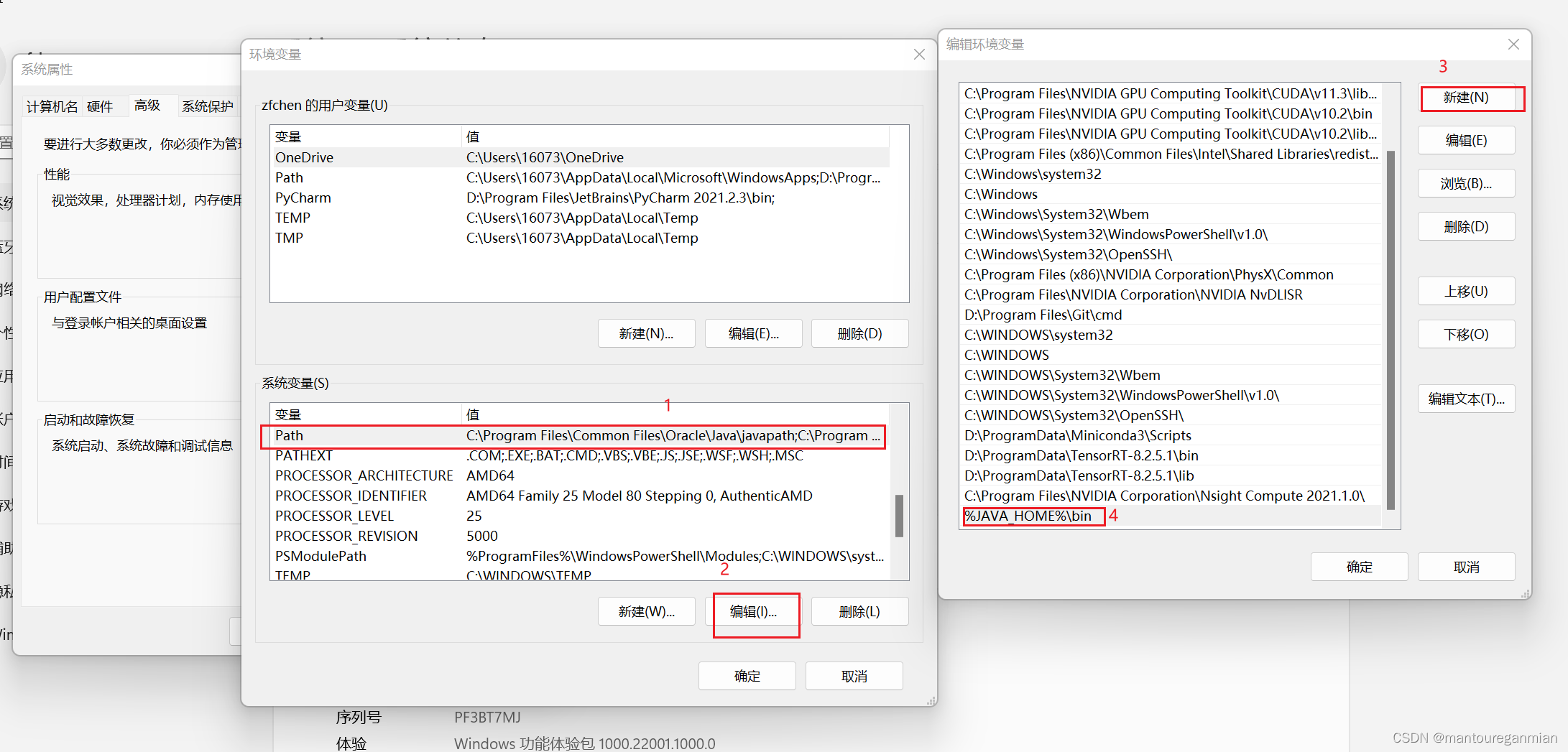
知识图谱小白入门(1):neo4j的安装与CQL的使用
文章目录 序一、安装neo4j1.1 下载neo4j1.2 安装JDK1.3 BUG:dbms failed to start 二、CQL语法2.1 CQL语法创建节点查询节点创建关系查询关系2.2 习题 习题答案 序 知识图谱,是一种实体间的信息与关系知识的网状结构,借用图论中点与边的概念…...

一个用java的get请求
java发送一个get请求,请求参数classyanfa,使用Authorization认证,在Request Header里填充Authorization: Bearer {token}进行请求认证,token为:sadagdagdgdgfagfd ,另外在Header里补充App标识,X…...
作为SiteGPT替代品,HelpLook的优势是什么?
在当今快节奏的数字化世界中,企业不断寻求创新方式来简化运营并增强客户体验。由于聊天机器人能够自动化任务、提供快速响应并提供个性化互动,它们在业务运营中的使用变得非常重要。因此,企业越来越意识到像SiteGPT和HelpLook这样高效的聊天机…...
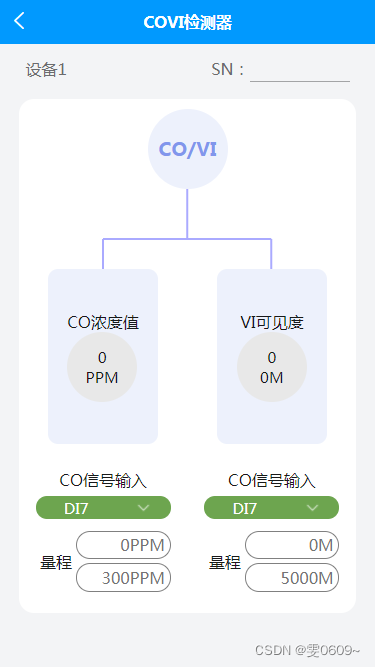
uni-app:实现页面效果2(canvas绘制,根据页面宽度调整元素位置)
效果 代码 <template><view><!-- 车搭配指示器-双显 --><view class"content_position"><view class"content"><view class"SN"><view class"SN_title">设备1</view><view class…...
)
【24种设计模式】责任链模式(Chain of Responsibility Pattern)
责任链模式是一种行为设计模式,它允许你将请求沿着处理链进行传递,直到有一个处理者能够处理该请求为止。这种模式将请求的发送者和接收者解耦,使多个对象都有机会处理该请求。 责任链模式的结构 责任链模式由以下几个角色组成:…...

微信小程序一对多个页面间传递数据进行通信,事件触发的实现方法
在有些场景下,使用组件间通信或者组件和页面间通信并不可行。比如我需要只有一个websocket实例,并且需要向多个页面传递我接收到的消息。 下面的方法是一个页面向其它页面(触发事件)传递数据,其它页面也可以向这个页面…...
软件测试之Python基础学习
目录 一、Python基础 Python简介、环境搭建及包管理 Python简介 环境搭建 包管理 Python基本语法 缩进(Python有非常严格的要求) 一行多条语句 断行 注释 变量 基本数据类型(6种) 1. 数字Number 2. 字符串String 3. 列表List 4. 元组Tuple 序列相关操作方法 …...

模块化编程+LCD1602调试工具——“51单片机”
各位CSDN的uu们你们好呀,小雅兰又来啦,刚刚学完静态数码管显示和动态数码管显示,感觉真不错呢,下面,小雅兰就要开始学习模块化编程以及LCD1602调试工具的知识了,让我们进入51单片机的世界吧!&am…...

【Linux】UDP的服务端 + 客户端
文章目录 📖 前言1. TCP和UDP2. 网络字节序2.1 大小端字节序:2.2 转换接口: 3. socket接口3.1 sockaddr结构:3.2 配置sockaddr_in:3.3 inet_addr:3.4 inet_ntoa:3.5 bind绑定: 4. 服…...

德国自动驾驶卡车公司【Fernride】完成1900万美元A轮融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于德国沃尔夫斯堡的自动驾驶卡车公司【Fernride】今日宣布已完成1900万美元A轮融资,本轮融资完成后Fernride的融资金额已经达到了达到5000万美元。 本轮融资由Deep Tech and Cli…...

实现水平垂直居中的十种方式
本文节选自我的博客:实现水平垂直居中的十种方式 💖 作者简介:大家好,我是MilesChen,偏前端的全栈开发者。📝 CSDN主页:爱吃糖的猫🔥📣 我的博客:爱吃糖的猫&…...

头条号热点采集工具-头条号热文采集软件
有一种魔法,能让信息传遍大地,让新闻在互联网上迅速传播,引发关注和讨论,那就是头条热点。无论你是一名自媒体创作者,还是一个信息追踪者,头条热点都是你不能忽视的宝贵资源。然而,如何获取这些…...

了解”变分下界“
“变分下界”:在变分推断中,我们试图找到一个近似概率分布q(x)来逼近真实的概率分布p(x)。变分下界是一种用于评估近似概率分布质量的指标,通常用来求解最优的近似分布。它的计算涉及到对概率分布的积分或期望的估计...

Andriod 简单控件
目录 一、文本显示1.1 设置文本内容1.2 设置文本大小1.3 设置文本颜色 二、视图基础2.1 设置视图宽高2.2 设置视图间距2.3 设置视图对齐方式 三、常用布局3.1 线性布局LinearLayout3.2 相对布局RelativeLayout3.3 网格布局GridLayout3.4 滚动视图ScrollView 四、按钮触控4.1 按…...

Substructure‑aware subgraph reasoning for inductive relation prediction
摘要 关系预测的目的是推断知识图中实体之间缺失的关系,其中归纳关系预测因其适用于新兴实体的有效性而广受欢迎。大多数现有方法学习逻辑组合规则或利用子图来预测缺失关系。尽管在性能方面已经取得了很大的进展,但目前的模型仍然不是最优的,因为它们捕获拓扑信息的能力有…...

古诗词学习鉴赏APP设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
