作为SiteGPT替代品,HelpLook的优势是什么?

在当今快节奏的数字化世界中,企业不断寻求创新方式来简化运营并增强客户体验。由于聊天机器人能够自动化任务、提供快速响应并提供个性化互动,它们在业务运营中的使用变得非常重要。因此,企业越来越意识到像SiteGPT和HelpLook这样高效的聊天机器人创建工具的必要性。两者都非常优秀,但HelpLook具有比较独特的优势,使其成为“SiteGPT替代品”。接下来我将跟大家深入探讨一下HelpLook的特点和优势。
| HelpLook有什么特点
HelpLook在功能丰富性、操作简便性和AI智能支持方面都很优秀,能够帮你更好地搭建和管理聊天机器人,并提供全方位的支持与帮助。
1. 快速搭建:HelpLook可以快速搭建免费的帮助中心站点/知识库/博客,无需代码和编程,只需要几分钟就可以完成搭建。
2. 全方位支持:HelpLook可以为你的产品提供全方位的支持与帮助,解决用户在使用过程中遇到的问题,提升用户体验感。
3. AI搜索服务:HelpLook接入了ChatGPT,支持基于文档的AI搜索服务,用户可以快速获取问题答案,提高问题解决效率。
4. 定制化问答机器人:HelpLook可以基于现有知识数据与AI模型,定制企业级专属的AI问答机器人,帮助用户更快速、精准地定位所需内容,解决难题。
5. 简单易用:HelpLook操作简单易上手,不需要专业技能,即使是非技术人员也可以轻松使用。
6. 节省成本:通过使用HelpLook创建聊天机器人,你可以节省人力成本,提高工作效率,让办公工作更加轻松。
| 为什么选择HelpLook而不是SiteGPT
对于中文用户来说,在性能和准确性方面HelpLook更好。首先,HelpLook经过大量数据的严格训练,而且是咱们国内自己的工具,使其能够生成更精确、与上下文相关的回答。这种提高的准确性转化为了更好的客户体验和企业的生产力提升。
而且HelpLook的一个显著特点是可定制的训练流程。企业可以使用其专有数据或领域特定知识对模型进行训练,从而获得更准确和行业特定的回答。这种定制水平使组织能够创建符合其独特工作流程的定制化AI解决方案。感兴趣的可以通过邀请码免费体验哦~【LookLook111】
| 结论
总而言之,HelpLook凭借其先进的功能和优势成为“SiteGPT替代品”,通过使用HelpLook,企业可以利用先进的人工智能能力获得竞争优势,推动创新和成功。
相关文章:

作为SiteGPT替代品,HelpLook的优势是什么?
在当今快节奏的数字化世界中,企业不断寻求创新方式来简化运营并增强客户体验。由于聊天机器人能够自动化任务、提供快速响应并提供个性化互动,它们在业务运营中的使用变得非常重要。因此,企业越来越意识到像SiteGPT和HelpLook这样高效的聊天机…...
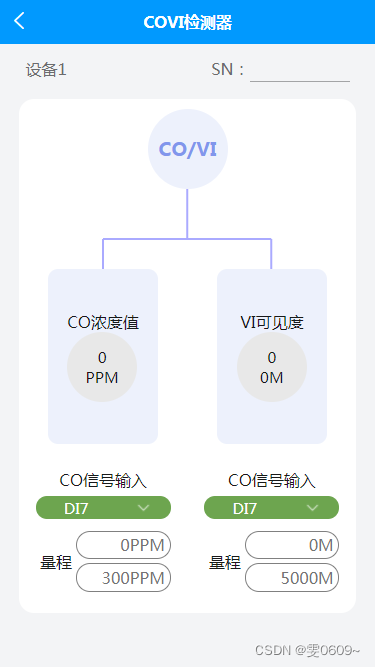
uni-app:实现页面效果2(canvas绘制,根据页面宽度调整元素位置)
效果 代码 <template><view><!-- 车搭配指示器-双显 --><view class"content_position"><view class"content"><view class"SN"><view class"SN_title">设备1</view><view class…...
)
【24种设计模式】责任链模式(Chain of Responsibility Pattern)
责任链模式是一种行为设计模式,它允许你将请求沿着处理链进行传递,直到有一个处理者能够处理该请求为止。这种模式将请求的发送者和接收者解耦,使多个对象都有机会处理该请求。 责任链模式的结构 责任链模式由以下几个角色组成:…...

微信小程序一对多个页面间传递数据进行通信,事件触发的实现方法
在有些场景下,使用组件间通信或者组件和页面间通信并不可行。比如我需要只有一个websocket实例,并且需要向多个页面传递我接收到的消息。 下面的方法是一个页面向其它页面(触发事件)传递数据,其它页面也可以向这个页面…...
软件测试之Python基础学习
目录 一、Python基础 Python简介、环境搭建及包管理 Python简介 环境搭建 包管理 Python基本语法 缩进(Python有非常严格的要求) 一行多条语句 断行 注释 变量 基本数据类型(6种) 1. 数字Number 2. 字符串String 3. 列表List 4. 元组Tuple 序列相关操作方法 …...

模块化编程+LCD1602调试工具——“51单片机”
各位CSDN的uu们你们好呀,小雅兰又来啦,刚刚学完静态数码管显示和动态数码管显示,感觉真不错呢,下面,小雅兰就要开始学习模块化编程以及LCD1602调试工具的知识了,让我们进入51单片机的世界吧!&am…...

【Linux】UDP的服务端 + 客户端
文章目录 📖 前言1. TCP和UDP2. 网络字节序2.1 大小端字节序:2.2 转换接口: 3. socket接口3.1 sockaddr结构:3.2 配置sockaddr_in:3.3 inet_addr:3.4 inet_ntoa:3.5 bind绑定: 4. 服…...

德国自动驾驶卡车公司【Fernride】完成1900万美元A轮融资
来源:猛兽财经 作者:猛兽财经 猛兽财经获悉,总部位于德国沃尔夫斯堡的自动驾驶卡车公司【Fernride】今日宣布已完成1900万美元A轮融资,本轮融资完成后Fernride的融资金额已经达到了达到5000万美元。 本轮融资由Deep Tech and Cli…...

实现水平垂直居中的十种方式
本文节选自我的博客:实现水平垂直居中的十种方式 💖 作者简介:大家好,我是MilesChen,偏前端的全栈开发者。📝 CSDN主页:爱吃糖的猫🔥📣 我的博客:爱吃糖的猫&…...

头条号热点采集工具-头条号热文采集软件
有一种魔法,能让信息传遍大地,让新闻在互联网上迅速传播,引发关注和讨论,那就是头条热点。无论你是一名自媒体创作者,还是一个信息追踪者,头条热点都是你不能忽视的宝贵资源。然而,如何获取这些…...

了解”变分下界“
“变分下界”:在变分推断中,我们试图找到一个近似概率分布q(x)来逼近真实的概率分布p(x)。变分下界是一种用于评估近似概率分布质量的指标,通常用来求解最优的近似分布。它的计算涉及到对概率分布的积分或期望的估计...

Andriod 简单控件
目录 一、文本显示1.1 设置文本内容1.2 设置文本大小1.3 设置文本颜色 二、视图基础2.1 设置视图宽高2.2 设置视图间距2.3 设置视图对齐方式 三、常用布局3.1 线性布局LinearLayout3.2 相对布局RelativeLayout3.3 网格布局GridLayout3.4 滚动视图ScrollView 四、按钮触控4.1 按…...

Substructure‑aware subgraph reasoning for inductive relation prediction
摘要 关系预测的目的是推断知识图中实体之间缺失的关系,其中归纳关系预测因其适用于新兴实体的有效性而广受欢迎。大多数现有方法学习逻辑组合规则或利用子图来预测缺失关系。尽管在性能方面已经取得了很大的进展,但目前的模型仍然不是最优的,因为它们捕获拓扑信息的能力有…...

古诗词学习鉴赏APP设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

深度学习与python theano
文章目录 前言1.人工神经网络2.计算机神经网络3.反向传播4.梯度下降-cost 函数1.一维2.二维3.局部最优4.迁移学习 5. theano-GPU-CPU theano介绍1.安装2.基本用法1.回归2.分类 3.function用法4.shared 变量5.activation function6.Layer层7.regression 回归例子8.classificatio…...
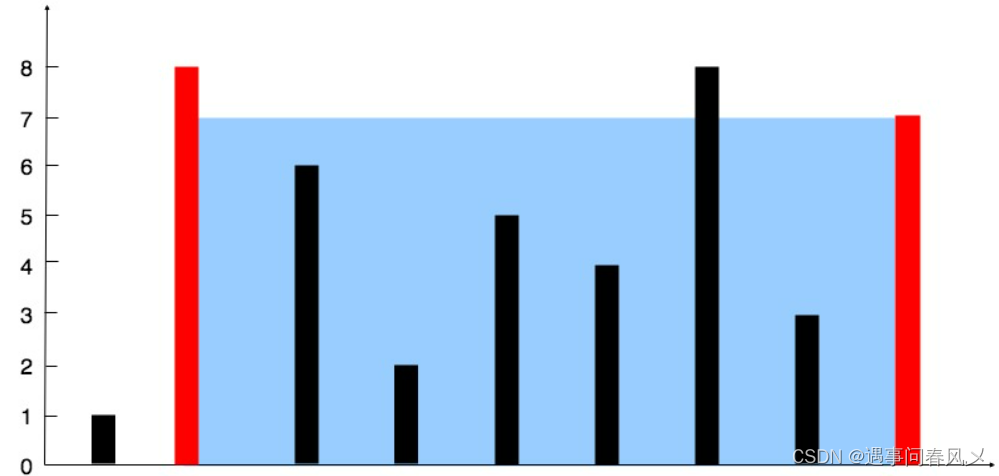
【算法优选】双指针专题——贰
文章目录 😎前言🌲[快乐数](https://leetcode.cn/problems/happy-number/)🚩题目描述🚩题⽬分析:🚩算法思路:🚩代码实现: 🎋[盛水最多的容器](https://leetco…...

AI智能电话机器人实用吗
近几年,人工智能得到很大的发展,同时语音识别技术的不断完善,很多以语音识别为基础的应用涌现出来,尤其是最近3年,出现了很多智能电话机器人。百度开发者大会上展示了百度智能客服也吸引了很多人对智能电话机器人的兴趣…...
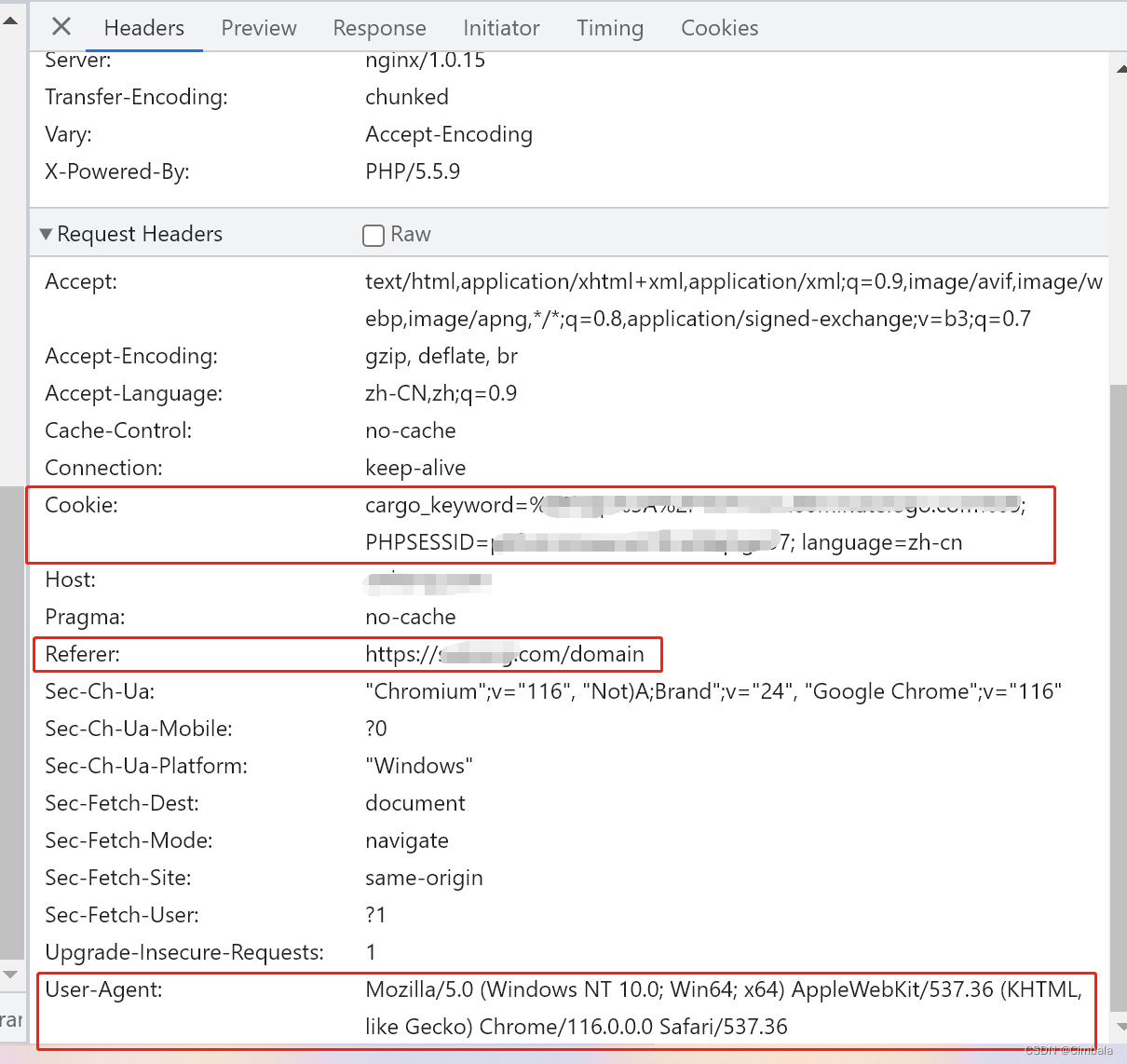
网络爬虫--伪装浏览器
从用户请求的Headers反反爬 在访问某些网站的时候,网站通常会用判断访问是否带有头文件来鉴别该访问是否为爬虫,用来作为反爬取的一种策略。很多网站都会对Headers的User-Agent进行检测,还有一部分网站会对Referer进行检测(一些资…...
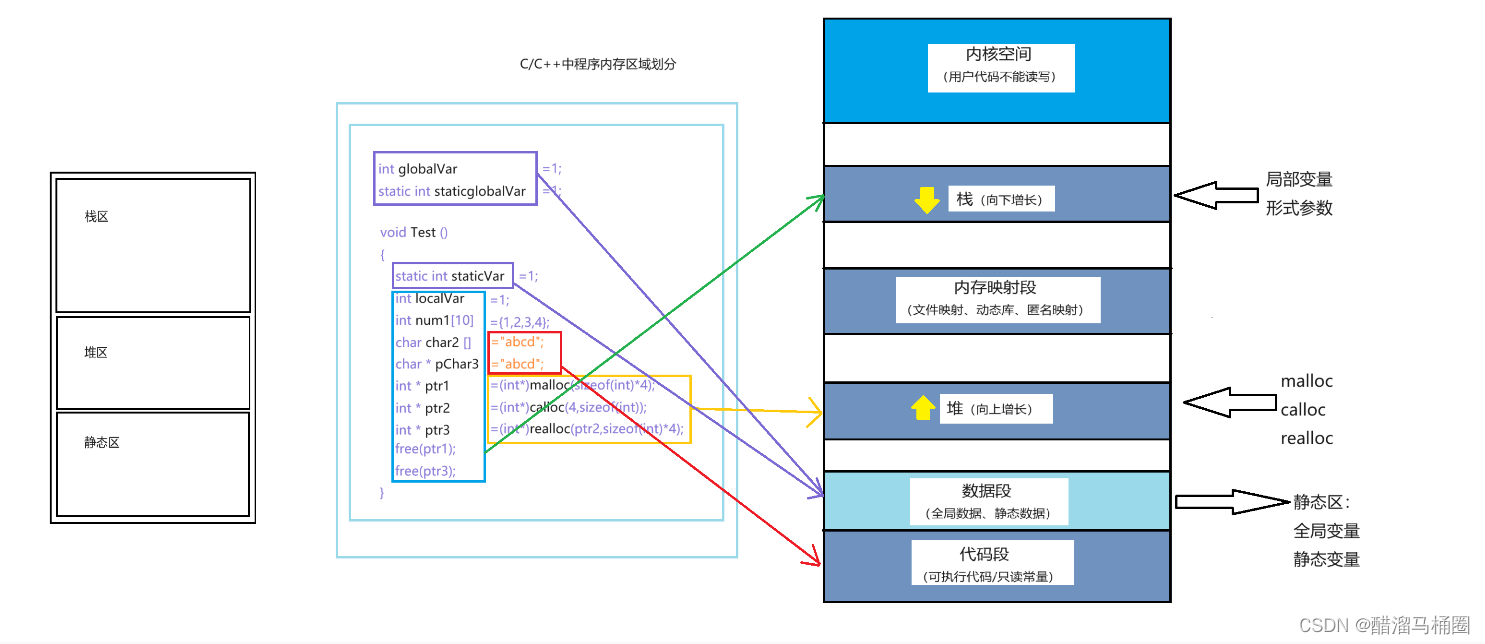
C/C++程序的内存开辟
前面我们说过,计算机中内存分为三个区域:栈区,堆区,静态区 但是这只是个简化的版本,接下来我们仔细看看内存区域的划分 C/C程序内存分配的几个区域: 栈区(stack):在执行…...

【Java 进阶篇】JDBC DriverManager 详解
JDBC(Java Database Connectivity)是 Java 标准库中用于与数据库进行交互的 API。它允许 Java 应用程序连接到各种不同的数据库管理系统(DBMS),执行 SQL 查询和更新操作,以及处理数据库事务。在 JDBC 中&am…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
)
window 显示驱动开发-如何查询视频处理功能(三)
D3DDDICAPS_GETPROCAMPRANGE请求类型 UMD 返回指向 DXVADDI_VALUERANGE 结构的指针,该结构包含特定视频流上特定 ProcAmp 控件属性允许的值范围。 Direct3D 运行时在D3DDDIARG_GETCAPS的 pInfo 成员指向的变量中为特定视频流的 ProcAmp 控件属性指定DXVADDI_QUER…...
