leetCode 674. 最长连续递增序列 动态规划 / 贪心策略
674. 最长连续递增序列 - 力扣(LeetCode)
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2] 输出:1 解释:最长连续递增序列是 [2], 长度为1。
>>思路和分析
本题相对于leetCode 300.最长递增子序列 最大区别在于 “连续”
- 不连续递增子序列的跟前0-i 个状态有关(两个for循环)
- 连续递增的子序列只跟前一个状态有关(一个for循环)
>>方法一:动态规划
1.确定dp数组(dp table)以及下标的含义
- dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]
注意这里的定义,一定是以下标i为结尾,并不是说一定以下标0为起始位置。
2.确定递推公式
如果 nums[i] > nums[i - 1],那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1
- 即:dp[i] = dp[i - 1] + 1;
3.dp数组初始化
以下标i为结尾的连续递增的子序列长度最少也应该是1,即就是nums[i]这一个元素。所以dp[i]应该初始1;
4.确定遍历顺序
从递推公式上可以看出, dp[i + 1]依赖dp[i],所以一定是从前向后遍历
for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i - 1]) { // 连续记录dp[i] = dp[i - 1] + 1;}
}5.举例推导dp数组

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if (nums.size() == 0) return 0;int result = 1;vector<int> dp(nums.size() ,1);for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i - 1]) { // 连续记录dp[i] = dp[i - 1] + 1;}if (dp[i] > result) result = dp[i];}return result;}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
>>方法二:贪心策略
当遇到nums[i] > nums[i - 1]的情况,count++,否则count 为 1,记录下count的最大值即可

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {if (nums.size() == 0) return 0;int count=1;int result=1;// 连续子序列最少也是1for(int i=1;i<nums.size();i++) {// 连续记录if(nums[i]>nums[i-1]) count = count + 1;// 不连续,count从头开始else count=1;result = max(count,result);}return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
>>来自代码随想录课堂截图:

>>参考和推荐文章、视频
代码随想录 (programmercarl.com)
动态规划之子序列问题,重点在于连续!| LeetCode:674.最长连续递增序列_哔哩哔哩_bilibili
相关文章:

leetCode 674. 最长连续递增序列 动态规划 / 贪心策略
674. 最长连续递增序列 - 力扣(LeetCode) 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。 连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每…...
数据中台实战(11)-数据中台的数据安全解决方案
0 微盟删库跑路 除了快、准和省,数据中台须安全,避免“微盟删库跑路”。 2020年2月23日19点,国内最大精准营销服务商微盟出现大面积系统故障,旗下300万商户线上业务全停,商铺后台所有数据被清。始作俑者是一位运维&a…...

林沛满-TCP之在途字节数
本文整理自:《Wireshark网络分析的艺术 第1版》 作者:林沛满 著 出版时间:2016-02 我一直谨记斯蒂芬霍金的金玉良言—每写一道数学公式就会失去一半读者。不过为了深度分析网络包,有时候是不得不计算的,好在小学一年级…...
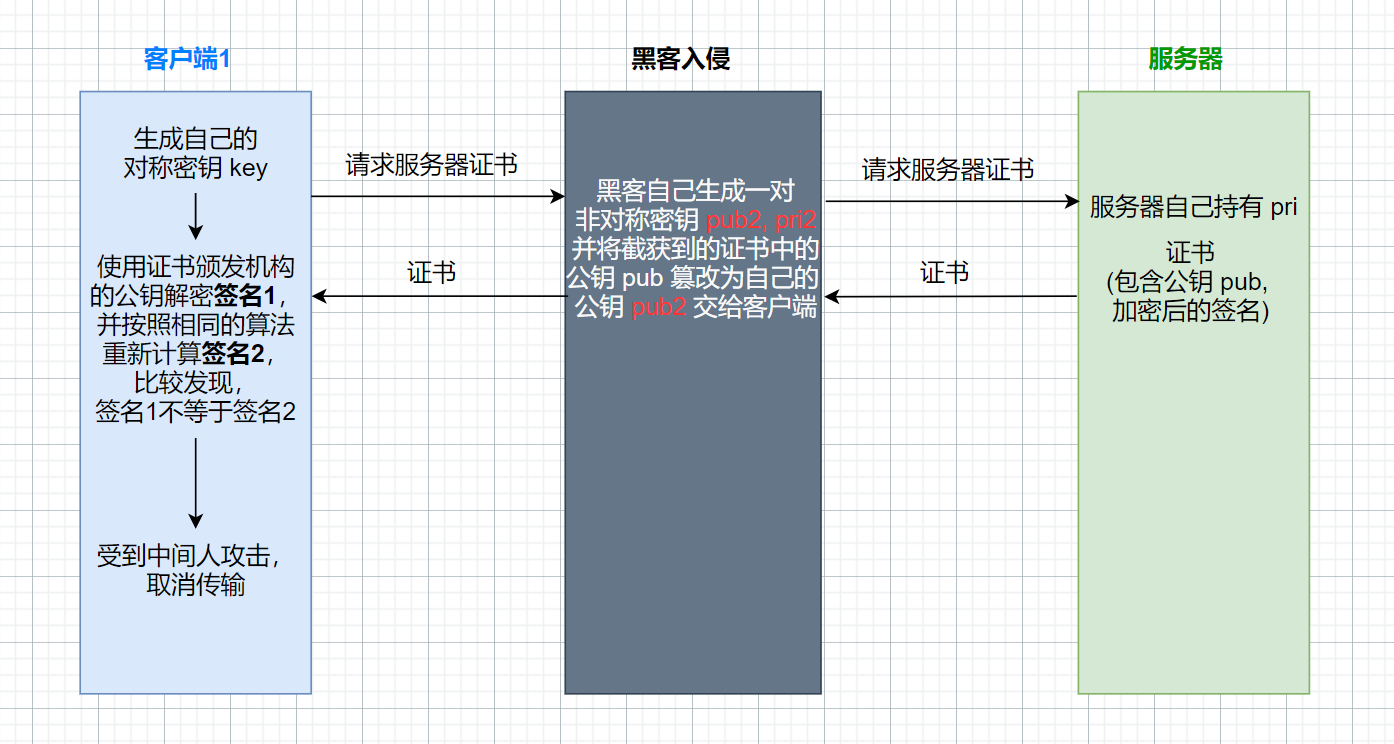
HTTPS 加密工作过程
引言 HTTP 协议内容都是按照文本的方式明文传输的,这就导致在传输过程中出现一些被篡改的情况。例如臭名昭著的运营商劫持。显然, 明文传输是比较危险的事情,为此引入 HTTPS ,HTTPS 就是在 HTTP 的基础上进行了加密, 进一步的来保…...
校招秋招,性格和职业有关系吗?
企业在招聘应届毕业生时不再局限于普通的面试或者笔试,在互联网时代,为了能够更好的匹配需要的优质人才,企业会通过各种测试来提高招聘的准确率以及成功率。也许以前很多人都听说过性格和职业是有一定关系的,但是如何确定自己的性…...
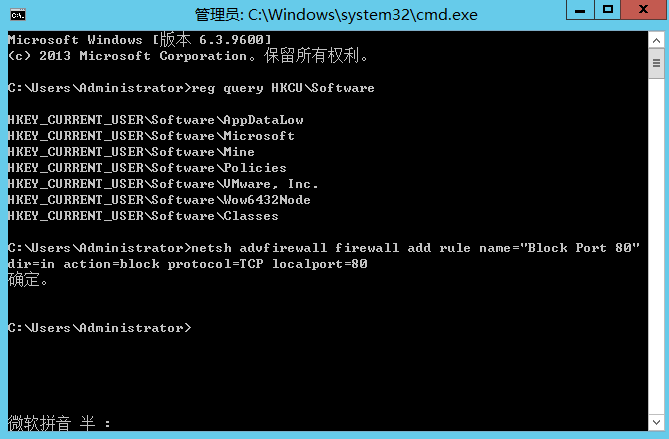
网络和系统操作命令
目录 ping:用于检测网络是否通畅,以及网络时延情况。ipconfig:查看计算机的IP参数配置信息,如IP地址、默认网关、子网掩码等信息。netstat:显示协议统计信息和当前TCP/IP网络连接。tasklist:显示当前运行的…...
)
刷穿力扣(1~30)
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 1. 两数之和 哈希表遍历数组,同时用 HashMap 维护已出现过的数及其下标若当前的数 nums[i] 满足 target - nums[i] 曾经出现过,则直接返回否则将其加入到哈希表中。 class Solution …...

栈和队列的基本操作
(一)实验类型:设计性 (二)实验目的: 1.掌握栈和队列的抽象数据类型。 2.掌握实现栈和队列的各种操作的算法。 3.理解栈与递归的关系。 4. 掌握队列的链式存贮结构及基…...

变压器绕组断股往往导致直流电阻不平衡率超标
变压器绕组断股往往导致直流电阻不平衡率超标, 例如, 某电厂 SFPSL—12000/220 型主变压器, 色谱分析结果发现总烃含量急剧增长, 测直流电阻, 其结果是高、 低压侧与制造厂及历年的数值相比较无异常, 但中压…...
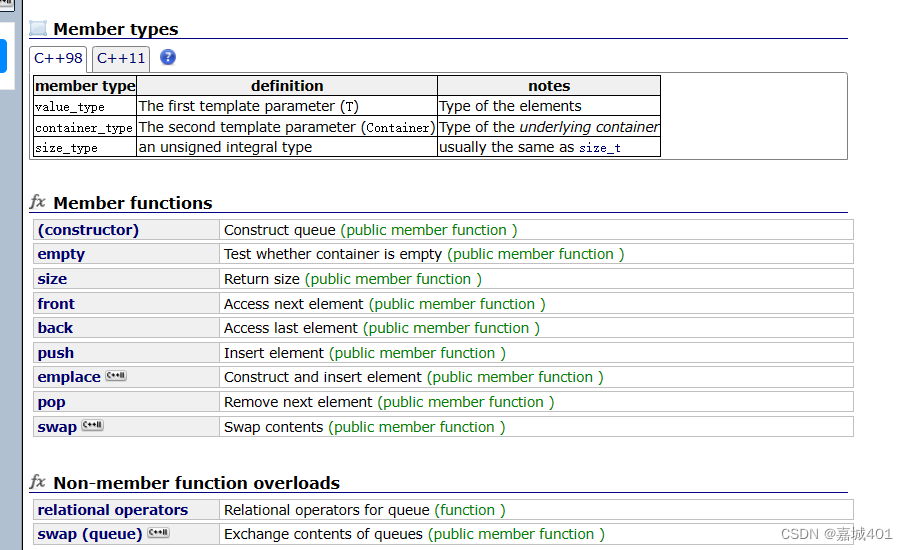
stack和queque
1.stack 1.1定义 T 是容器内的数据类型; Container是数据类型的容器适配器 vector和list和stack的区别 1.2 stack的功能 注意这里没有迭代器;原因stack是先进后出的规律;这就规定该容器不可以随机访问; 2. queue...

信息学 学习/复习 抽签器(附源码)
问你一个问题,你考试前怎么复习呀? 效果图 以下是源代码,可自行修改 [C] #include<bits/stdc.h> #include<windows.h> using namespace std; vector<string>item; int main(void) {item.push_back("Manacher"…...
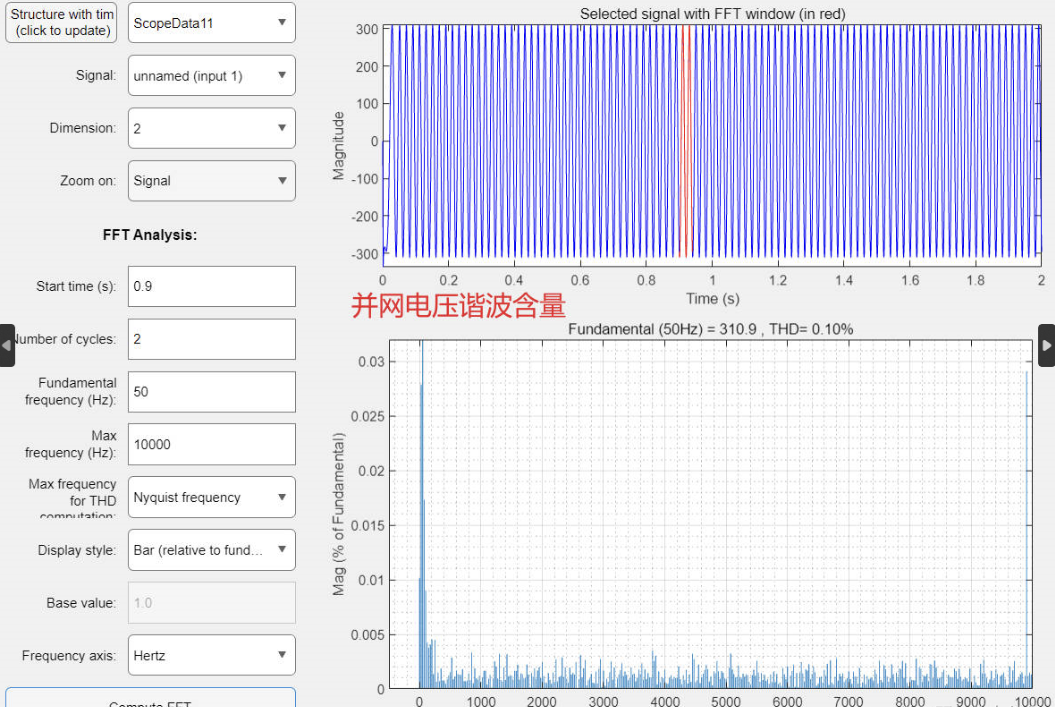
基于LADRC自抗扰控制的VSG三相逆变器预同步并网控制策略(Simulink仿真实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

[0xGame 2023] week1
整理一下,昨天该第二周了。今天应该9点结束提交,等我写完就到了。 PWN 找不到且不对劲的flag 第1题是个nc测试,但也不完全是,因为flag在隐含目录里 高端的syscall 程序使用了危险函数,并且没有canary阻止࿰…...

Matlab矩阵——矩阵行列互换
问题:如何将 1*n 的矩阵转换为指定 M*N 的矩阵,或者将 M*N 的矩阵转换为 1*n 的矩阵? 处理方法:使用 reshape 函数进行矩阵的行列互换 分两种情况如下: 一、将 1*n 的矩阵转换为指定 M*N 的矩阵 假如有4个坐标值&a…...

OpenMesh 网格面片随机赋色
文章目录 一、简介二、实现代码三、实现效果一、简介 OpenMesh中的赋色方式与Easy3D很是类似,它统一有一个属性数组来进行管理,我们在进行赋色等操作时,必须要首先添加该属性才能进行使用,这里也进行记录一下(法向量等特征也是类似的操作)。 二、实现代码 #define _USE_…...
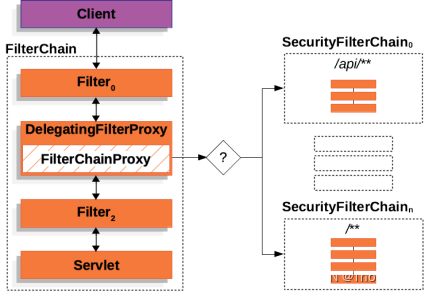
SpringSecurity源码学习一:过滤器执行原理
目录 1. web过滤器Filter1.1 filter核心类1.2 GenericFilterBean1.3 DelegatingFilterProxy1.3.1 原理1.3.2 DelegatingFilterProxy源码 2. FilterChainProxy源码学习2.1 源码2.1.1 doFilterInternal方法源码2.1.1.1 getFilters()方法源码2.1.1.2 VirtualFilterChain方法源码 3…...
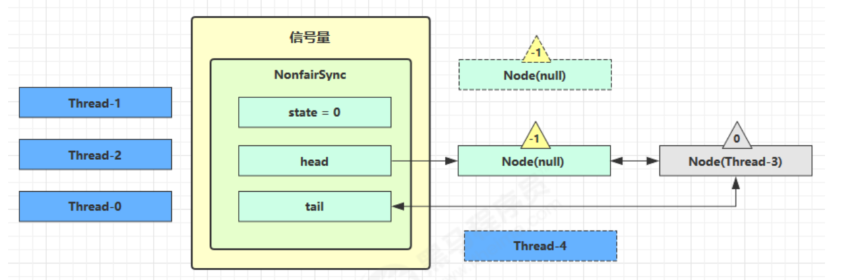
8.2 JUC - 4.Semaphore
目录 一、是什么?二、简单使用三、semaphore应用四、Semaphore原理 一、是什么? Semaphore:信号量,用来限制能同时访问共享资源的线程上限 二、简单使用 public class TestSemaphore {public static void main(String[] args) …...

前端try和catch
为什么要使用try catch 使用try...catch语句是为了处理和管理可能会在程序运行过程中发生的异常或错误情况。以下是一些使用try...catch的主要原因: 错误处理:在开发过程中,无法避免地会出现各种错误,如网络请求失败、数据解析错误…...

Unity可视化Shader工具ASE介绍——2、ASE的Shader创建和输入输出
大家好,我是阿赵,这里继续介绍Unity可视化写Shader的ASE插件的用法。上一篇介绍了ASE的安装和编辑器界面分布,这一篇主要是通过一个简单的例子介绍shader的创建和输入输出。 一、ASE的Shader创建 这里先选择Surface类型的Shader,…...
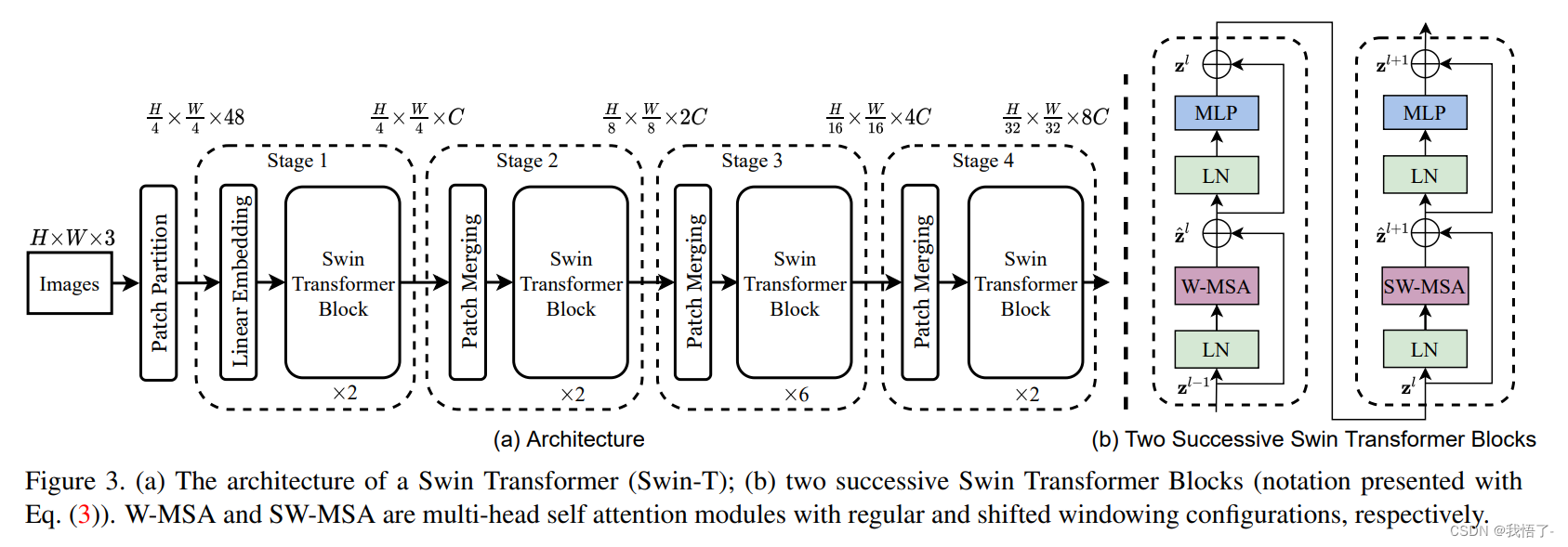
目标检测算法改进系列之Backbone替换为Swin Transformer
Swin Transformer简介 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》作为2021 ICCV最佳论文,屠榜了各大CV任务,性能优于DeiT、ViT和EfficientNet等主干网络,已经替代经典的CNN架构,成为了计算机…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
