维吉尼亚密码
维吉尼亚密码属于多表代换密码

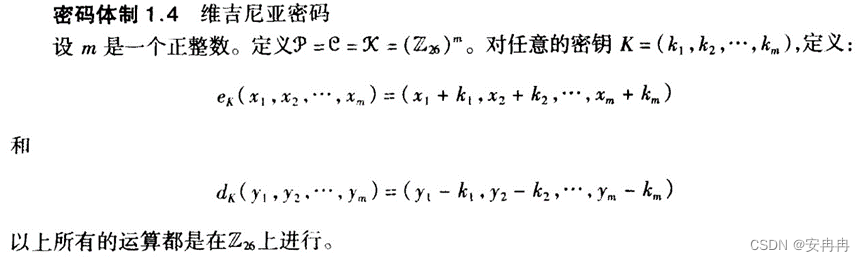
其中A<–>0,B<–>1,…,Z<–>25,则每个密钥K相当于一个长度为m的字母串,称为密钥字。维吉尼亚密码一次加密m个明文字母。
示例:设m=6,密钥字为“CIPHER”,对应数字串K=(2,8,15,7,4,17)。要加密明文为:thiscrypto,则
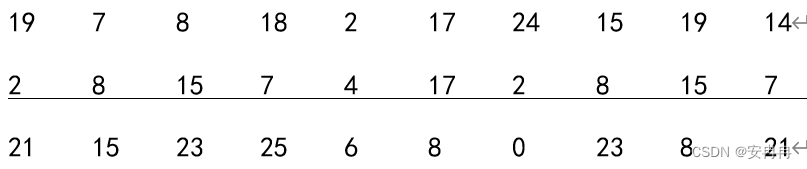 则相应的密文为:VPXZGIAXIV
则相应的密文为:VPXZGIAXIV
解密时,使用相同的密钥字进行逆运算即可。
可以看出,维吉尼亚密码的密钥空间为26^m。
加密:
Plaintext = 'THISCRYPTO'#字母需要大写
K = [2,8,15,7,4,17]#print(K)#密钥Ciphertext = ''
for i in range(len(Plaintext)):M_i = ord(Plaintext[i]) - 65 K_i = K[i%len(K)]C_i = (M_i+K_i)%26Ciphertext += chr(C_i+ 65)
print(Ciphertext)解密:
Ciphertext = 'VPXZGIAXIV'
K = [2,8,15,7,4,17]Plaintext = ''
for i in range(len(Ciphertext)):C_i = ord(Ciphertext[i]) -65 K_i = K[i%len(K)]M_i = (C_i - K_i)%26Plaintext += chr(M_i+ 65)
print(Plaintext)相关文章:

维吉尼亚密码
维吉尼亚密码属于多表代换密码 其中A<–>0,B<–>1,…,Z<–>25,则每个密钥K相当于一个长度为m的字母串,称为密钥字。维吉尼亚密码一次加密m个明文字母。 示例:设m6,密钥字为…...

ubuntu20.04挂载拓展盘保姆级流程
背景:跑模型玩时,发现机子硬盘太小了,搞个1t固态作为挂载盘。以下为操作全流程记录 1、开始root权限操作 sudo su若进不去,考虑是否给root设置过密码,新系统第一次进入需要设置密码。 进入成功: rooty:…...
)
顶顶通电话机器人接口对接开源ASR(语音识别)
前景介绍 目前大部分用户使用的都是在线ASR按照分钟或者按次付费,之前开源ASR效果太差不具备商用的条件,随着 阿里达摩院发布了大量开源数据集或者海量工业数据训练的模型,识别效果已经和商用ASR差距非常小,完全具备了很多场景代…...

windows消息机制
windows开发比较简单,首先要理解的就是消息机制。 Windows消息机制是指Windows操作系统中的消息传递机制。在Windows中,应用程序通过消息进行通信和交互。消息是一种轻量级的通信方式,用于在不同的窗口、线程或进程之间传递信息。 在Windows…...

整数划分——DP
用 j j j 个数表示 i i i 的方案数,考虑dp 转移考虑最小值是否为1 无限制 若为1,则转移到 f ( i 1 , j 1 ) f(i1, j1) f(i1,j1)不为1,则全部1,转移到 f ( i j , j ) f(ij, j) f(ij,j) 数之间不能重复 那么相当于每次整…...

Git切换用户常用命令
1、查看 查看用户名 : git config user.name查看密码: git config user.password查看邮箱: git config user.email查看配置信息(包含上面的信息): $ git config --list2、新增、切换 修改用户名 git…...

一般香港服务器带宽选多大够用?(带宽计算方法)
在海外IDC市场份额中,香港服务器依托自身优越的服务器资源条件,在各个行业中发挥的重要作用。但是,不同业务对网络带宽的要求各不相同,弄清楚如何计算带宽需求对于确保业务平稳运行至关重要,最好从一开始就使用正…...

vue中使用ali-oss上传文件到阿里云上
1.使用 npm 安装ali-oss npm install ali-oss --save2.写ali-oss.js // 引入ali-oss let OSS require(ali-oss) let client new OSS({region: oss-cn-xxx, // bucket所在的区域, 默认oss-cn-hangzhousecure: true, // secure: 配合region使用,如果指…...
计算时间的函数及其示例说明)
php实战案例记录(17)计算时间的函数及其示例说明
在PHP中,有许多函数可以用于计算和处理时间。以下是一些常用的计算时间的函数及其示例说明: time():获取当前时间的Unix时间戳。 $currentTimestamp time(); echo $currentTimestamp;date():将Unix时间戳格式化为指定的日期和时…...

基于Keil a51汇编 —— MPL 宏定义
MPL 宏 Ax51汇编程序支持的宏处理语言(MPL)是一种字符串替换工具,使您能够编写可修复的代码块(宏)并将其插入源文本中的一个或多个位置。 宏处理器查看源文件的方式与汇编程序不同。 对于汇编程序来说,源…...
——点击拍照到存入相册)
Android 13 骁龙相机点击拍照流程分析(二)——点击拍照到存入相册
一.前言 本篇是在Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图文章的基础上进行延申的,前面的预览、点击拍照的过程参考第一篇:Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图-CSDN博客 二.生成图片并保存 从第…...
)
常见算法-巴斯卡三角形(Pascal)
常见算法-巴斯卡三角形(Pascal) 1、说明 巴斯卡(Pascal)三角形基本上就是在解 nCr,因为三角形上的每一个数字各对应一个nCr,其中 n 为 row,而 r 为 column,如下: 0C0 1…...

AI:09-基于深度学习的图像场景分类
图像场景分类是计算机视觉领域的重要任务之一,它涉及将图像分为不同的场景类别,如城市街景、山脉风景、海滩等。本文将介绍基于深度学习的图像场景分类方法,并提供相应的代码实例,展示了深度学习在图像场景分类中的技术深度和应用前景。 图像场景分类是计算机视觉中的一项…...
uni-app:引入echarts(使用renderjs)
效果 代码 <template><view click"echarts.onClick" :prop"option" :change:prop"echarts.updateEcharts" id"echarts" class"echarts"></view> </template><script>export default {data()…...
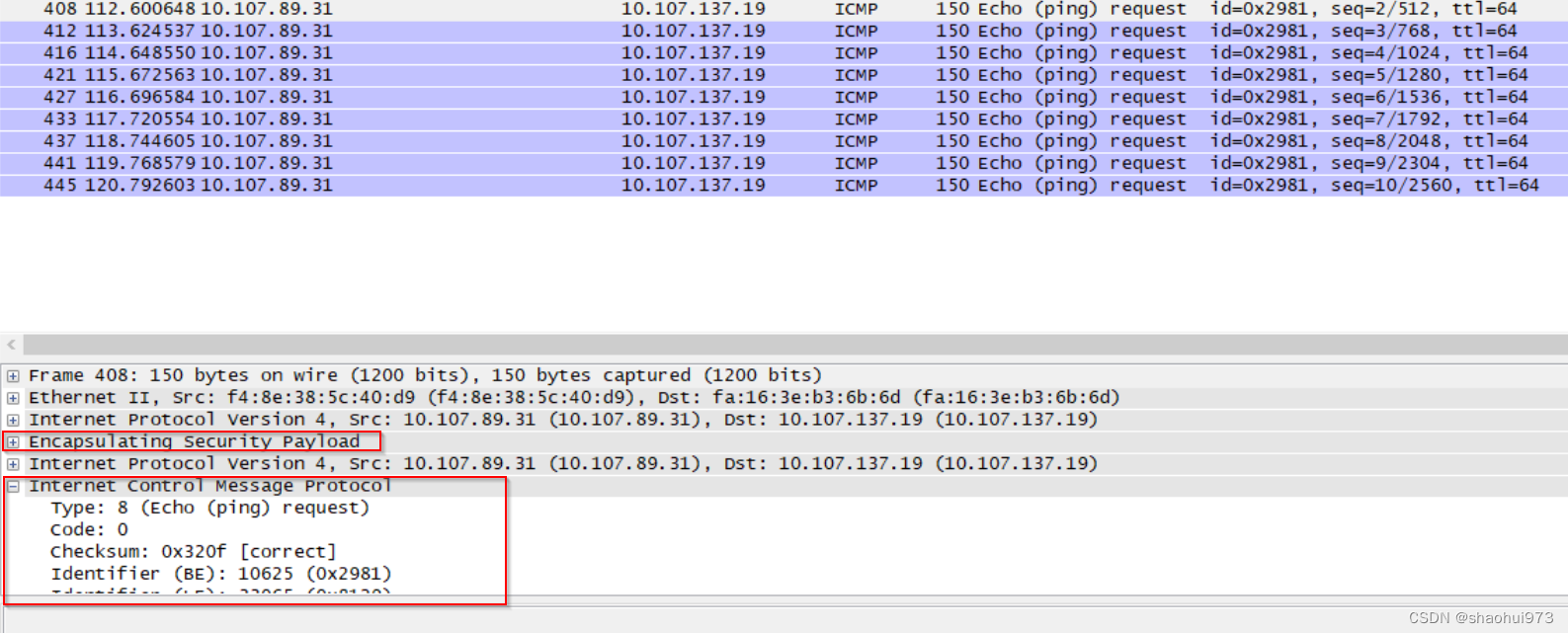
使用wireshark解析ipsec esp包
Ipsec esp包就是ipsec通过ike协议协商好后建立的通信隧道使用的加密包,该加密包里面就是用户的数据,比如通过的语音等。 那么如何将抓出来的esp包解析出来看呢? 获取相关的esp的key信息. 打开wireshark -> edit->preferences 找到pr…...

linux如何删除最近操作的日志
Linux系统下,不同的应用程序可能会生成不同的日志文件。如果你想要删除最近一段时间内的操作日志,可以使用一些命令来完成。 以下是一些常见的命令: dmesg:该命令用于显示内核环境下的运行信息和警告信息。如果你需要清空dmesg缓…...

android端MifareClassicTool
github地址 GitHub - ikarus23/MifareClassicTool: An Android NFC app for reading, writing, analyzing, etc. MIFARE Classic RFID tags. 开源项目 下载: https://www.icaria.de/mct/releases/ 功能 1、读取Mifare Classic卡片 2、编辑并保存卡片的数据 3、写入Mifare C…...
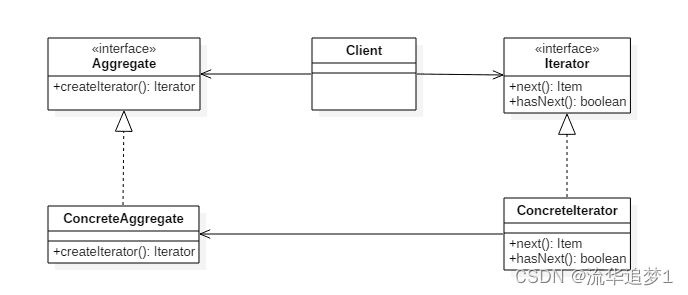
设计模式 - 迭代器模式
目录 一. 前言 二. 实现 三. 优缺点 一. 前言 迭代器模式是一种行为型设计模式,它提供了一种统一的方式来访问集合对象中的元素,而不暴露集合内部的表示方式。简单地说,就是将遍历集合的责任封装到一个单独的对象中,我们可以按…...
Docker之Dockerfile搭建lnmp
目录 一、搭建nginx 编辑 二、搭建Mysql(简略版) 三、搭建PHP 五、补充 主机名ip地址主要软件mysql2192.168.11.22Docker 代码示例 systemctl stop firewalld systemctl disable firewalld setenforce 0docker network create --subnet172.18.…...
排序算法——选择排序
一、介绍: 选择排序就是按照一定的顺序从选取第一个元素索引开始,将其储存在一个变量值中,根据排序规则比较后边每一个元素与这个元素的大小,根据排序规则需要,变量值的索引值进行替换,一轮遍历之后&#x…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

运动控制--BLDC电机
一、电机的分类 按照供电电源 1.直流电机 1.1 有刷直流电机(BDC) 通过电刷与换向器实现电流方向切换,典型应用于电动工具、玩具等 1.2 无刷直流电机(BLDC) 电子换向替代机械电刷,具有高可靠性,常用于无人机、高端家电…...

如何使用CodeRider插件在IDEA中生成代码
一、环境搭建与插件安装 1.1 环境准备 名称要求说明操作系统Windows 11JetBrains IDEIntelliJ IDEA 2025.1.1.1 (Community Edition)硬件配置推荐16GB内存50GB磁盘空间 1.2 插件安装流程 步骤1:市场安装 打开IDEA,进入File → Settings → Plugins搜…...
