Python 编程基础 | 第三章-数据类型 | 3.6、元组
一、元组
Python 的元组与列表类似,不同之处在于元组的元素不能修改。元组使用小括号,列表使用方括号。
1、创建元组
元组创建很简单,只需要在括号中添加元素,并使用逗号隔开即可,例如:
tup1 = ('physics', 'chemistry', 1997, 2000)
tup2 = (1, 2, 3, 4, 5 )
tup3 = "a", "b", "c", "d"
2、访问元组
元组可以使用下标索引来访问元组中的值,例如:
tup1 = ('physics', 'chemistry', 1997, 2000)
tup2 = (1, 2, 3, 4, 5, 6, 7 )print(tup1[0]) # 输出结果:physics
print(tup1[:3]) # 输出结果:('physics', 'chemistry', 1997)
3、删除元组
元组中的元素值是不允许删除的,但我们可以使用del语句来删除整个元组,例如:
tup1 = ('physics', 'chemistry', 1997, 2000)
tup2 = (1, 2, 3, 4, 5, 6, 7 )del(tup1) # 删除元组tup1
print(tup1) # 编译报错:NameError: name 'tup1' is not defined. Did you mean: 'tup2'?
4、元组运算符
与字符串一样,元组之间可以使用 + 号和 * 号进行运算。这就意味着他们可以组合和复制,运算后会生成一个新的元组。
| 表达式 | 结果 | 描述 |
|---|---|---|
| len((1, 2, 3)) | 3 | 计算元素个数 |
| (1, 2, 3) + (4, 5, 6) | (1, 2, 3, 4, 5, 6) | 链接 |
| (‘Hi!’,) * 4 | (‘Hi!’, ‘Hi!’, ‘Hi!’, ‘Hi!’) | 复制 |
| 3 in (1, 2, 3) | True | 元素是否存在 |
| for x in (1, 2, 3): print x | 1 2 3 | 遍历 |
5、元组内置函数
Python元组包含了以下内置函数
| 函数 | 功能 |
|---|---|
| cmp(tuple1, tuple2) | 比较两个元组元素 |
| len(tuple) | 计算元组元素个数 |
| max(tuple) | 返回元组中元素最大值 |
| min(tuple) | 返回元组中元素最小值 |
| tuple(seq) | 将列表转换为元组 |
相关文章:

Python 编程基础 | 第三章-数据类型 | 3.6、元组
一、元组 Python 的元组与列表类似,不同之处在于元组的元素不能修改。元组使用小括号,列表使用方括号。 1、创建元组 元组创建很简单,只需要在括号中添加元素,并使用逗号隔开即可,例如: tup1 (physics, ch…...

2023/10/7 -- ARM
【程序状态寄存器读写指令】 1.指令码以及格式 mrs:读取CPSR寄存器的值 mrs 目标寄存器 CPSR:读取CPSR的数值保存到目标寄存器中msr:修改CPSR寄存器的数值msr CPSR,第一操作数:将第一操作数的数值保存到CPSR寄存器中//修改CPSR寄存器,也就表示程序的状…...

yolov5加关键点回归
文章目录 一、数据1)数据准备2)标注文件说明 二、基于yolov5-face 修改自己的yolov5加关键点回归1、dataloader,py2、augmentations.py3、loss.py4、yolo.py 一、数据 1)数据准备 1、手动创建文件夹: yolov5-face-master/data/widerface/tr…...
untitle
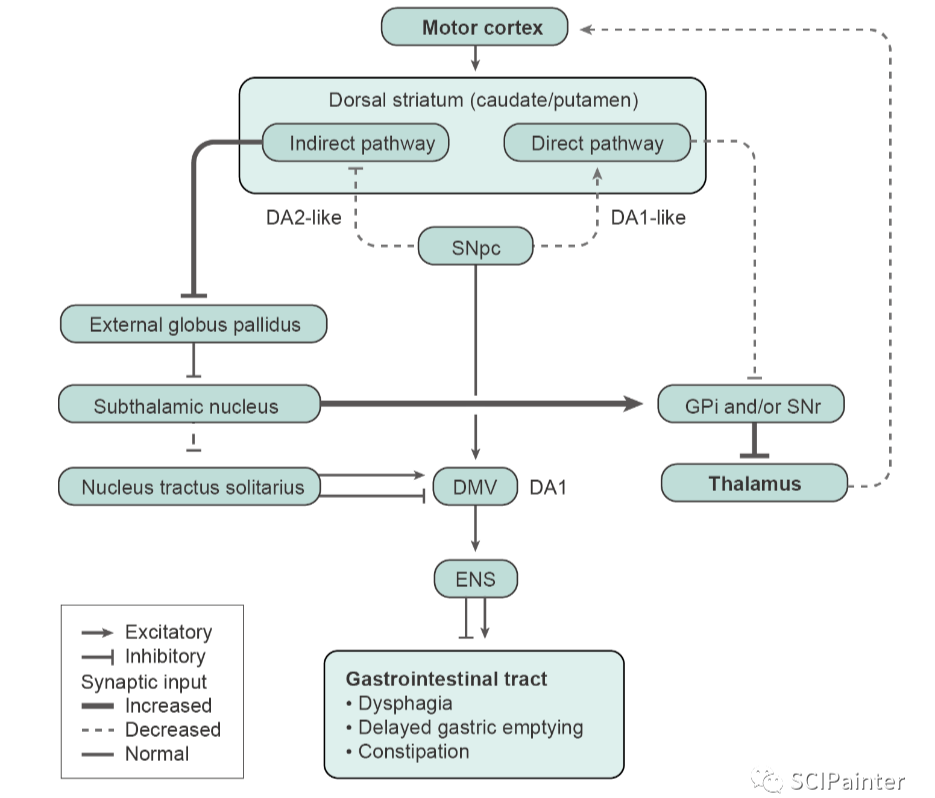
实用的科研图形美化处理教程分享 显微照片排版标记 除了统计图表之外,显微照片也是文章中必不可少的实验结果呈现方式。除了常规实验的各种组织切片照片,在空间转录组文章中显微照片更是常见。显微照片的呈现方式也是有讲究的,比如对照片…...

《论文阅读》监督对抗性对比学习在对话中的情绪识别 ACL2023
《论文阅读》监督对抗性对比学习在对话中的情绪识别 前言摘要相关知识最坏样本干扰监督对比学习生成式对抗网络纳什均衡琴森香农散度范式球模型架构监督对抗性对比学习模型结构图实验结果问题前言 你是否也对于理解论文存在困惑? 你是否也像我之前搜索论文解读,得到只是中文…...

2023-10-07 LeetCode每日一题(股票价格跨度)
2023-10-07每日一题 一、题目编号 901. 股票价格跨度二、题目链接 点击跳转到题目位置 三、题目描述 设计一个算法收集某些股票的每日报价,并返回该股票当日价格的 跨度 。 当日股票价格的 跨度 被定义为股票价格小于或等于今天价格的最大连续日数(…...
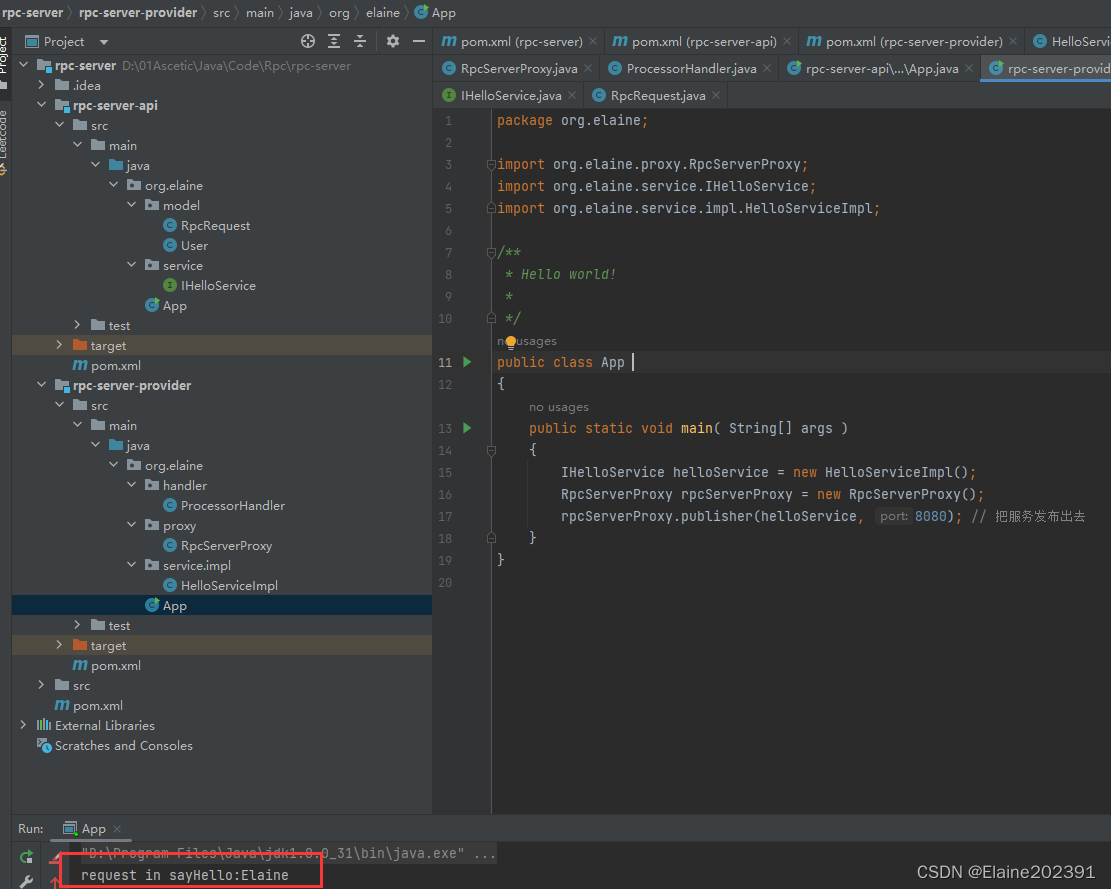
聊聊分布式架构04——RPC通信原理
目录 RPC通信的基本原理 RPC结构 手撸简陋版RPC 知识点梳理 1.Socket套接字通信机制 2.通信过程的序列化与反序列化 3.动态代理 4.反射 思维流程梳理 码起来 服务端时序图 服务端—Api与Provider模块 客户端时序图 RPC通信的基本原理 RPC(Remote Proc…...
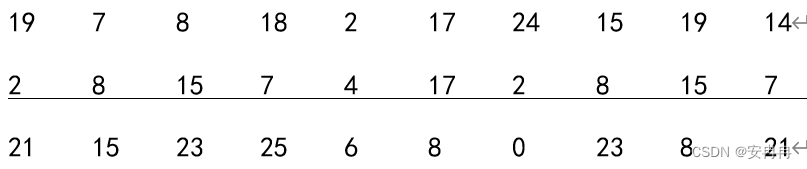
维吉尼亚密码
维吉尼亚密码属于多表代换密码 其中A<–>0,B<–>1,…,Z<–>25,则每个密钥K相当于一个长度为m的字母串,称为密钥字。维吉尼亚密码一次加密m个明文字母。 示例:设m6,密钥字为…...

ubuntu20.04挂载拓展盘保姆级流程
背景:跑模型玩时,发现机子硬盘太小了,搞个1t固态作为挂载盘。以下为操作全流程记录 1、开始root权限操作 sudo su若进不去,考虑是否给root设置过密码,新系统第一次进入需要设置密码。 进入成功: rooty:…...
)
顶顶通电话机器人接口对接开源ASR(语音识别)
前景介绍 目前大部分用户使用的都是在线ASR按照分钟或者按次付费,之前开源ASR效果太差不具备商用的条件,随着 阿里达摩院发布了大量开源数据集或者海量工业数据训练的模型,识别效果已经和商用ASR差距非常小,完全具备了很多场景代…...

windows消息机制
windows开发比较简单,首先要理解的就是消息机制。 Windows消息机制是指Windows操作系统中的消息传递机制。在Windows中,应用程序通过消息进行通信和交互。消息是一种轻量级的通信方式,用于在不同的窗口、线程或进程之间传递信息。 在Windows…...

整数划分——DP
用 j j j 个数表示 i i i 的方案数,考虑dp 转移考虑最小值是否为1 无限制 若为1,则转移到 f ( i 1 , j 1 ) f(i1, j1) f(i1,j1)不为1,则全部1,转移到 f ( i j , j ) f(ij, j) f(ij,j) 数之间不能重复 那么相当于每次整…...

Git切换用户常用命令
1、查看 查看用户名 : git config user.name查看密码: git config user.password查看邮箱: git config user.email查看配置信息(包含上面的信息): $ git config --list2、新增、切换 修改用户名 git…...

一般香港服务器带宽选多大够用?(带宽计算方法)
在海外IDC市场份额中,香港服务器依托自身优越的服务器资源条件,在各个行业中发挥的重要作用。但是,不同业务对网络带宽的要求各不相同,弄清楚如何计算带宽需求对于确保业务平稳运行至关重要,最好从一开始就使用正…...

vue中使用ali-oss上传文件到阿里云上
1.使用 npm 安装ali-oss npm install ali-oss --save2.写ali-oss.js // 引入ali-oss let OSS require(ali-oss) let client new OSS({region: oss-cn-xxx, // bucket所在的区域, 默认oss-cn-hangzhousecure: true, // secure: 配合region使用,如果指…...
计算时间的函数及其示例说明)
php实战案例记录(17)计算时间的函数及其示例说明
在PHP中,有许多函数可以用于计算和处理时间。以下是一些常用的计算时间的函数及其示例说明: time():获取当前时间的Unix时间戳。 $currentTimestamp time(); echo $currentTimestamp;date():将Unix时间戳格式化为指定的日期和时…...

基于Keil a51汇编 —— MPL 宏定义
MPL 宏 Ax51汇编程序支持的宏处理语言(MPL)是一种字符串替换工具,使您能够编写可修复的代码块(宏)并将其插入源文本中的一个或多个位置。 宏处理器查看源文件的方式与汇编程序不同。 对于汇编程序来说,源…...
——点击拍照到存入相册)
Android 13 骁龙相机点击拍照流程分析(二)——点击拍照到存入相册
一.前言 本篇是在Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图文章的基础上进行延申的,前面的预览、点击拍照的过程参考第一篇:Android 13 骁龙相机点击拍照流程分析(一)——点击拍照到更新到左下角缩略图-CSDN博客 二.生成图片并保存 从第…...
)
常见算法-巴斯卡三角形(Pascal)
常见算法-巴斯卡三角形(Pascal) 1、说明 巴斯卡(Pascal)三角形基本上就是在解 nCr,因为三角形上的每一个数字各对应一个nCr,其中 n 为 row,而 r 为 column,如下: 0C0 1…...

AI:09-基于深度学习的图像场景分类
图像场景分类是计算机视觉领域的重要任务之一,它涉及将图像分为不同的场景类别,如城市街景、山脉风景、海滩等。本文将介绍基于深度学习的图像场景分类方法,并提供相应的代码实例,展示了深度学习在图像场景分类中的技术深度和应用前景。 图像场景分类是计算机视觉中的一项…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
